基于同源的抗量子群密钥交换协议

樊雪君，王龙，徐秀，宋宁宁，范晶，王怡

(1.华北计算机系统工程研究所，北京 100083；2.中国信息通信研究院，北京 100191)

0 引言

基于同源的密码协议是抗量子密码中的重要组成部分，它依赖于计算给定椭圆曲线之间同源的困难性，该困难问题在量子算法攻击下的时间复杂度是(亚)指数级别的。目前基于同源的密钥交换协议有三类：OIDH(基于常曲线同源的密钥交换协议)、SIDH(基于超奇异同源的密钥交换协议)和CSIDH(基于可交换的超奇异同源的密钥交换协议)。相比于其他抗量子密码协议，基于同源的密码体制的优势是密钥长度短，劣势是协议效率低。本文主要考虑了基于同源的群密钥交换协议，从调整协议的模型的角度来讨论基于同源的密钥交换协议的加速。

1 研究背景及研究内容

1.1 研究背景

群密钥交换(GKE)协议允许多个参与方在公共网络上协商共享密钥，现已被广泛地应用于现实世界的交互网络中，比如Ad-hoc网络和无线传感网络等。目前大部分的群密钥交换方案[1-3]都是从两方的密钥交换协议扩展而来的。

但是目前针对抗量子的群密钥交换方案还比较少。Apon等人[4]将BD协议推广到环LWE问题上，得到了格上的群密钥交换协议。基于同源的群密钥交换协议也逐渐得到关注，Furukawa等人[5]提出了两个基于超奇异同源的多方密钥交换协议。第一个是SIDH协议的变形，域的特征变为参与方的数量会影响p的选取。第二个是传统BD协议[1]的变形，但其乘法运算的数量较多，降低了协议的效率。Azarderakhsh等人[6]构造了n方群密钥交换协议，每个用户在发送下一条信息之前都必须使用自己的私钥信息进行计算，即提供了隐式认证，但是该方案也有很多缺陷：第一，如果参与方的数量n发生了变化，则有限域的特征也需要更改；第二，方案每个用户需要计算n-1个同源和(n-1)n个点的像，单个用户传输的比特数可达到O(λn2)(λ是安全参数)量级，故方案的计算复杂度和通信量较高；第三，该方案没有安全性证明。因此，研究基于超奇异同源的群密钥交换协议是非常有意义的。

1.2 本文工作及结构

本文提出了两个2轮的基于超奇异同源的抗量子群密钥交换协议。第一个是对基于超奇异同源的BD协议—SIBD协议[5]的加速。由于BD协议中单个用户的通信量较高，研究者们便考虑了树形的BDII模型[7]，故本文的第二个方案便是SIDH和BDII协议[3]的结合。在这两个GKE协议中，本文都更换了会话密钥的计算方式，使用有限域中的加减法而不是乘除法来进行计算，从而提高了整个协议的计算效率，使其可以被微型处理器接受。此外本文还给出了两个方案针对被动攻击者的安全性证明，最后对协议的轮数、通信量以及计算复杂度进行了分析。与现有的基于超奇异同源的GKE协议[5]比较，本文所提协议具有较小的计算复杂度和较高的通信效率。

2 基础知识

2.1 SIDH协议

2.1.1 SIDH协议形式

De Feo等人[8]利用Fp2上的超奇异椭圆曲线构造了SIDH协议。由于Fp2上的超奇异椭圆曲线的自同态环是非交换的，故SIDH协议的量子攻击复杂度为指数时间[9]。

SIDH协议[6]使用了有理点的个数有很多小素数做因子的超奇异曲线，这样曲线有很多小次数的同源，从而可提高计算效率。特别地，取超奇异椭圆曲线E/Fp2，其中是 素 数，lA和lB是 小素数，f是使得p是素数的调节因数，则#E/(Fp2)=(或是Fp2有理的，且包含个阶为的循环子群，这些循环子群对应了不同构的同源。令是 公共参数，SIDH协议的具体执行过程如图1所示。

图1 基于Fp2上的超奇异椭圆曲线的密钥交换协议(SIDH)

Alice和Bob通过密钥交换分别获得曲线EAB和EBA， 且因此协议双方可共享EAB和EBA的j-不变量。

值得注意的是，Alice的私钥mA、nA不能同时被lA整 除，以 保 证对Bob的 私 钥mB、nB也 有类似要求。在具体执行过程中，一般取lA=2，lB=3。且为了减少标量乘的计算、提高协议的效率，会不失一般性地取mA=mB=1，且nA和nB分别在和中随机均匀选取。

图2给出了更直观的协议双方进行的操作。

图2 SIDH协议的直观执行图

值得一提的是，基于SIDH协议构造的密钥封装协议SIKE[10]已经被提交到NIST算法竞赛中，并成为第三轮候选算法。

2.1.2 SIDH协议的基本困难问题

首先利用DH语言来描述一下SIDH协议，以便后续安全性证明中使用。

设{t，s}={0，1}，记公钥参数为g=(E0；P0，Q0，P1，Q1)和e=(l0；l1，e0，e1)。 定义超奇异椭圆曲线的集合及曲线和点构成三元组的集合：

SSECp={定义在Fp2上超奇异椭圆曲线

SSECA=是的基}

SSECB=是的基}

记a=ka且b=kb，则可以定义：

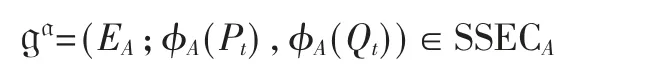
其 中RA=Ps+[ka]Qs，φA：E0→EA=E0/〈RA〉。

其 中RB=Pt+[kb]Qt，φB：E0→EB=E0/〈RB〉。

其中RBA=φB(Ps)+[ka]φB(Qs)，φBA：EB→EBA=EB/〈RBA〉。

其中RAB=φA(Pt)+[kb]φA(Qt)，φAB：EA→EAB=EA/〈RAB〉。

值得注意的是，本文定义ga和gb是群，而定义(gb)a和(ga)b是j-不变量。这并不是出现了错误，只是将SIDH协议的形式与传统的Diffie-Hellman(DH)密钥交换协议的形式结合起来。利用上述符号，便可发现SIDH协议的形式与DH协议形式几乎完全相同。公共参数为g和e，Alice选择私钥a并发送ga给Bob，Bob选择私钥b并发送gb给Alice，最终共享密钥为j=(gb)a=(ga)b。基于符号定义，本文描述两个关于超奇异同源的标准假设:

定义1(SI-DDH假设[7])给定公共参数g和e，定义两个分布D0和D1：

SI-DDH问题指的是，随机给定一个分布Db，其中b←{0，1}，猜测b的值。对于多项式时间的算法A，定义其解决SI-DDH问题的优势为：

则SI-DDH假设指的是，对于任意多项式时间的算法A，解决SI-DDH问题的优势都是可忽略的。

2.2 SIBD协议的安全模型

针对群密钥交换协议的安全性，由于本文是以SIDH协议为基础构造的群密钥交换协议，因此本文考虑文献[11]中的认证链接攻击者模型。在证明过程中假设所有协议的参与方都是诚实的。

假设协议中共有n个参与方U={U1，U1，…，Un}，每个参与者都可以同时运行多个事件。记参与者U的第i个事件为，会话标识为sid，会话参与者标识为pid。

GKE模型的安全性是由一系列挑战者和攻击者A之间的游戏定义的。在游戏过程中，敌手A可以通过询问下列问题解决某个挑战：：返回诚实执行过程中的交互信息。这是被动攻击所执行的。

Corrupt(Ui)：该询问泄露Ui的静态密钥。如果敌手未进行Corrupt询问，则参与者是诚实的。：在接受事件中进行该询问，该询问在整个执行过程中只能出现一次。

在安全性证明的过程中，允许敌手A执行Test询问。令κ是当前会话过程中的会话密钥，挑战者随机选取b∈{1，0}，若b=1则向敌手发送当前的会话密钥；否则便向敌手发送密钥空间中的随机元素。如果敌手在会话s过期之前就向相应的oracle询问了s或者，则称参与方的会话都是本地公开的。如果s在过期之前，s或者其匹配会话s′是本地公开的，则称s被暴露；否则，证s是新鲜的会话。

在Test询问的前后，攻击者都可以进行自适应的查询，即询问挑战者关于测试会话以外的其他问题。最后，攻击者A猜测比特b′，令SuccA(λ)是挑战者A猜对b=b′的概率，其中λ是安全参数，则定义：

定义2(Session-Key安全)设密钥交换协议的安全参数为λ，若对于任意多项式时间的敌手A，均满足：若未被Corrupt询问的两方完成了匹配会话，则会话便输出相同的密钥，且AdvA(λ)是可忽略的。则称该密钥交换协议是Session-Key安全的。

3 改进的基于超奇异同源的群密钥交换协议

本节将SIDH协议分别与BD协议和BDII协议结合，并利用加法运算代替会话密钥计算过程中的乘法运算，从而得到了更高效的2轮群密钥交换协议。

3.1 改进的SIBD协议

Furukawa等人[5]以SIDH协议为基础推广BDI协议，从而得到了SIBD协议。本文将其会话密钥计算过程中的乘除法更换为加减法，从而优化了SIBD协议，还给出了抵抗被动攻击的安全性证明。

群密钥交换协议中的公共参数与SIDH协议的公共参数相同，设协议中共有n个参与方，依次标号为1，2，…，n，记Un+1=U1，则n个参与方可构成一个环形。当n是奇数时，可以使其中某个参与者虚拟地扮演两个角色。因此可只考虑n是偶数的情况。下面为改进的SIBD协议流程。

第1轮：每个用户Ui随机选取作为私钥，计算Ri=Ps+kiQs，其中s=i(mod 2)。然后计算同源φi：E→Ei=E/〈Ri〉，令，将广播给Ui-1和Ui+1。

第2轮：每个用户Ui收到相邻两方发送来的公钥和，利用收到的公钥和自己的私钥执行SIDH协议，可得和，其中ji-1，i和ji，i+1分 别 代 表 了Ei-1/〈φi-1(Ps)+kiφi-1(Qs)〉和Ei+1/〈φi+1(Ps)+kiφi+1(Qs)〉的j-不变量。最后，用户Ui向所有参与方广播。

计算会话密钥：每个用户Ui利用哈希函数H:{0，1}*→{0，1}λ，其 中λ是 安 全 参 数，计 算 会 话 密钥Ki=H(nji-1，i+(n-1)ui+(n-2)ui+1+…+2ui-3+ui-2)，可以验证，对于任意i，均有：

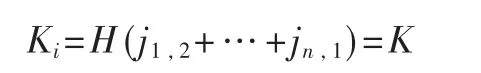
需要强调，相比于有限域中的乘法，加法计算的复杂度可以被忽略，这便是改进的SIBD协议效率提高的主要原因。关于安全强度，GKE协议中最基本的安全性要求便是SK-安全(SK-security)，即对被动攻击者来说会话密钥不可区分。

定理1在SI-DDH的假设下，改进的SIBD协议在随机谕言机模型下是安全的，并且可以达到前向安全性。即如果存在n个用户，敌手A询问qE次Execute，该协议满足。

证明：由于协议中没有静态密钥，故敌手可以忽略Corrupt询问，因此该协议满足前向安全性。

现假设存在敌手A可以攻击改进的SIBD协议，证明可以构造区分器D以不可忽略的优势解决SI-DDH问题。敌手A可以询问Execute、RevealKey和Test。设是一次执行过程的记录，K是该过程得到的会话密钥，则可定义两个分布Real和Fake。其中Real是真实协议执行产生的分布，而Fake中的是在Fp2中随机选取且满足记，φi：E→Ei=E/〈Ps+liQs〉，则：

断言1对于任意敌手A，有|Pr[(T，K)←Real：A(T，K)=1]-Pr[(T，K)←Fake′：A(T，K)=1]|≤，其中：

证明：设存在一个针对SI-DDH问题的区分器D。D调用敌手A，输入与SIDH协议中相同的(ga，gb，gc)，根据分布Dist′生成(T，K)，然后输出敌手A的输出结果。其中：

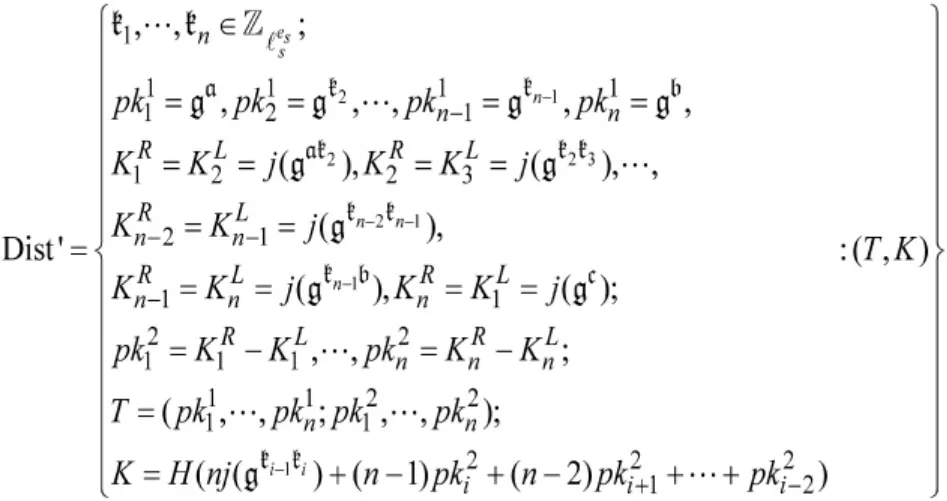
如果li是随机的，则分布Real与分布{a，b∈；(T，K)←Dist′：(T，K)}在统计意义下是等价的。此外，除了一个的因子，分布Fake′与分布{a，b∈在统计意义下是等价的。因此通过SI-DDH问题的归约可以得到分布Real和Fake′在统计意义下是等价的。

断言2对于任意敌手A，均有|Pr[(T，K)←Fake′：A(T，K)=1]-Pr[(T，K)←Fake：A(T，K)=1]|≤。

证明：仿照断言1中的结论，定义分布

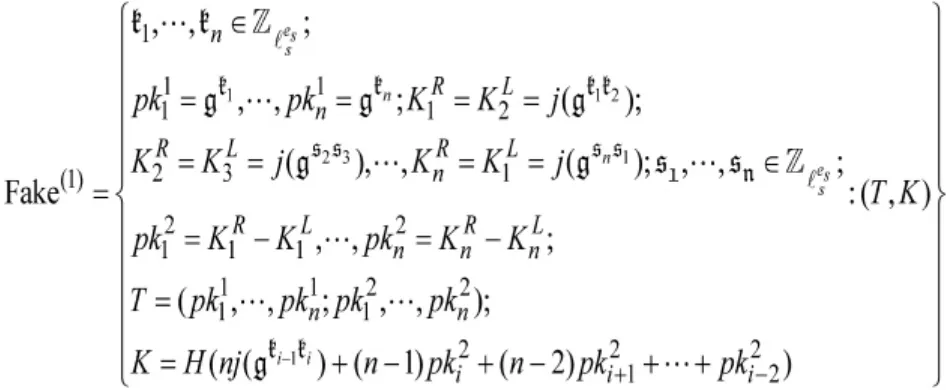
便可得：

|Pr[(T，K)←Fake：A(T，K)=1]-Pr[(T，K)←Fake(1)：A(T，K)=1]|≤

然后利用hybrid方法可以得到：

|Pr[(T，K)←Fake′：A(T，K)=1]-Pr[(T，K)←Fake：A(T，K)=1]|≤(n-1)

断言3对于任意敌手A，均有|Pr[(T，K0)←Fake；K1←Fp2；b←{0，1}：A(T，Kb)=b]|=。

综合以上三个断言可知：

qE次询问的过程都是类似的，因此2|Pr[T，K0]←Real，K1←Fp2，b←{0，1}：A(T，Kb)=b]-Pr[T，K0]←Fake，K1←Fp2，b←{0，1}：A(T，Kb)=。

定理1证毕。

3.2 改进的SIBDII协议

由于BD协议的通信量较高，故考虑使用树形结构的BDII协议。在广播版本中，BDII协议的每个用户的通信量和计算复杂度均为O(log(n))，故本节结合SIDH协议给出优化的SIBDII协议。协议中n个用户被标识为1，2，…，n(n为偶数)，且用户按照其标识被依次放置于树形结构上(如图3所示)。

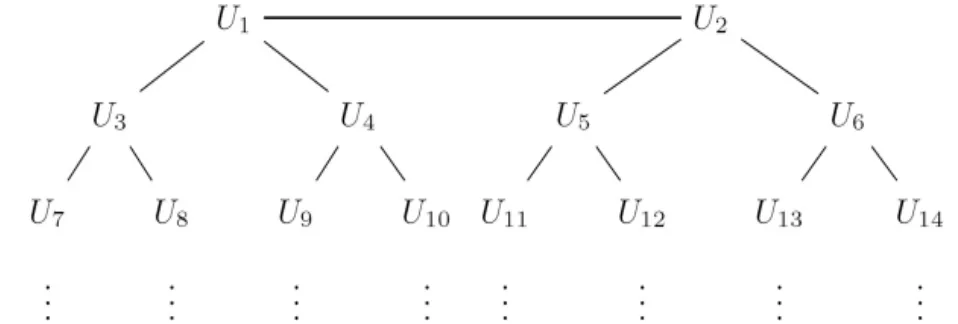
图3 BDII协议中的二元树

从图3中可以发现，用户Ui位于树的第■log2(i+1)」层。记用户Ui的父母、左孩子和右孩子的标识分别为parent(i)、lchild(i)和rchild(i)，U1和U2分别是对方的父母。则树上所有除叶子节点之外的节点均有一个父母和两个孩子。令ancestors(i)为用户Ui的所有祖先的标识构成的集合，其中i∈ancestors(i)但1，2∉ancestors(i)。为了保证用户Ui和Uparent(i)在公共曲线E的两个不同子集中进行计算，令s(1)=0，s=s(i)=s(parent(i))+1(mod 2)用于标识两个不同的子集。改进的SIBDII协议的公共参数与SIDH的参数相同，其具体执行过程如下：

第1轮：用户Ui随机选择私钥并计算Ri=Ps+kiQs，以〈Ri〉为 核 计 算 同 源φi：E→Ei=E/〈Ri〉，令，并将广播给父母和两个孩子。

第2轮：用户Ui收到父母及其两个孩子的公钥和，并利用这些公钥和自己的私钥执行SIDH密钥交换协议，可得。 然 后 用 户Ui计 算(jparent(i)，i-ji，lchild(i)，jparent(i)，i-ji，rchild(i))，并 将 结 果 广 播 给 其后代。

会话密钥计算：用户Ui利用哈希函数H:{0，1}*→{0，1}λ，其 中λ为 安 全 参 数， 计 算 会 话 密 钥Ki=其中Xm=jparent(parent(m))，parent(m)-jparent(m)，m。

容易验证，对于任意i均有Ki=H(j1，2)=K。值得注意的是，在改进的SIBDII协议中，仍使用加法运算来计算会话密钥，从而提高了整个协议的效率。

定理2在SI-DDH假设下，改进的SIBDII群密钥交换协议在随机谕言机模型下可抵抗被动攻击，并且满足前向安全性。即如果有n个参与者，敌手攻击k次会话过程，询问qE次Execute，则该方案满足。

证明：由于协议中没有静态密钥，敌手可以忽略Corrupt询问，故该协议满足前向安全性。

假设改进的SIBDII群密钥交换协议存在敌手A，可以构造区分器D调用A，以不可忽略的概率解决SI-DDH问题。敌手A可以询问Execute、RevealKey和Test。设是一次执行过程的记录，K是该过程得到的会话密钥，则可定义两个分布Real和Fake。其中Real是真实协议执行产生的 分 布，而Fake中 的是 在Fp2中 随 机 选 取 的。记。

使用hybrid方 法计算|Pr[T，K0]←Real，K1←Fp2，b←{0，1}：A(T，Kb)=b]-Pr[T，K0]←Fake，K1←Fp2，b←{0，1}：A(T，Kb)=b]|

需要定义分布：

断言4对于任意敌手A，均有|Pr[(T，K0)←Fake；K1←Fp2；b←{0，1}：A(T，Kb)=b]|=。

断言5对于任意敌手A′，均有|Pr[(T，K)←Real：A′(T，K)=1]-Pr[(T，K)←Fake1：A′(T，K)=，其中k是敌手攻击会话过程数目的上界。

断言6对于任意敌手A，均有|Pr[(T，K)←Fake：A′(T，K)=1]-Pr[(T，K)←Fake1：A′(T，K)=1]|=。

总结上述三个断言，可得：

定理2证毕。

4 协议比较

4.1 复杂度分析

改进的SIBD协议是BD协议的变形，本文更换了会话密钥的计算方式，将j-不变量之间的乘法变为加法。原SIBD协议[5]中需要次乘法，而改进的SIBD协议中只需要(n-1)次乘法和n次加法。改进的SIBDII协议是BDII协议的变形，其计算复杂度为O(log(n))。

一个群密钥交换协议的通信复杂度是由协议的轮数及各用户每次交互信息的大小决定的。选择参考文献[9]中的参数，在λ比特安全强度下，p的比特长度应为6λ，则Fp2中元素的比特长度为12λ。由于曲线是定义在Fp2上的，故曲线和点的表示都需要12λ bit(见表1)。

表1 群密钥交换协议的比较

表1中结果是以一个用户为单位来计算通信复杂度和计算复杂度的。而对于一次密钥交换过程中所有用户交互的总信息量来说，改进的SIBD协议中所有 用 户 交 互 信 息 的 总 和 为(12■log2(n+1)」+96)nλ bit，改进的SIBDII协议中所有用户交互信息的总和为。

4.2 环形结构和树形结构的比较

通过两类群密钥交换协议的通信复杂度和计算复杂度的比较可以发现：在树形结构的群密钥交换协议中，每个用户的通信复杂度和计算复杂度都是O(log(n))级别的；而在环形结构的群密钥交换协议中，通信复杂度和计算复杂度都是O(n)级别的(其中n为用户数量)。这是否意味着基于树形结构的群密钥交换协议更好呢？本小节主要比较了环形结构和树形结构在应用场景和计算性能等方面的表现。

首先假定协议的各个参与方的计算能力相当。否则，若存在一个可信用户Ui，其计算能力远大于其他用户的计算能力，则可以使用环形结构的变形：用户Ui与其他n-1个用户分别交互获得密钥，进行计算后再统一广播给其他参与方。此时用户Ui的计算复杂度是其他用户的n-1倍。在通信复杂度方面，记B是广播所需通信量，P是点对点交互所需的通信量，则用户Ui的通信量是2B+(n-1)P，其他用户的通信量为2P。

在计算复杂度方面，如果各个参与方的计算能力相当，环形结构的计算复杂度为O(n)量级，而树形结构的计算复杂度为O(log(n))量级，因此树形结构更优。在通信复杂度上，环形结构中用到了广播的通信模式，而树形结构中用到的是多方传播的通信模式。由于协议的参与方数量有限，因此此处不区分广播和多方传播的通信复杂度，则有如下比较(见表2)。

表2 树形结构和环形结构中单用户通信量比较

总之，尽管使用了环形结构的BD协议具有很好的代数结构，但是由于其总体的通信复杂度高，故很少被应用于实际场景中[12]。

5 结论

本文主要利用SIDH协议构造了两个改进的群密钥交换协议。通过安全性证明，本文所提出的协议可以归约到SI-DDH问题，因此在量子攻击下是安全的，此外，通过与现有的基于超奇异同源的群密钥交换协议比较，所提协议的计算复杂度和通信量都更低。