材料力学中关于斜弯曲定义的讨论
2022-05-25刘灵灵
刘灵灵
(石家庄铁道大学 工程力学系,河北 石家庄 050043)
0 引言
材料力学学习中,组合变形部分是综合性较强的内容,需要学生对该章之前的内容熟练掌握,再借助于对一些新概念的准确理解,才能真正学好本章知识。斜弯曲是组合变形中的一种情况,也是一个新概念,这一概念是与前面涉及的平面弯曲相对应的,那么什么时候发生平面弯曲?什么时候发生斜弯曲?两种不同的弯曲变形,变形之后挠曲线有什么特点?斜弯曲到底“斜”在哪里?学生在学习本部分内容时,往往会产生困惑。国内经典材料力学教材[1-4]针对这个概念,大致给出了两种定义,一种定义是以力与位移的方向是否一致来判断,另一种定义是考虑弯矩矢量方向与中性轴方向是否一致来判断,两种定义侧重点不同,对一些特殊情况的判断会有所差异,下面分别进行阐释。
1 斜弯曲的第一种定义
针对平面弯曲,教材[1-2]定义为:梁发生弯曲变形后,梁的挠曲线为外力作用平面内的一条平面曲线,教材[3]定义为:当梁上所有外力都在纵向对称平面内,弯曲变形后的轴线将是位于这个对称面内的一条曲线,教材[4]定义为:当所有外力都作用于杆件的同一主轴平面(形心主轴与梁的轴线构成的纵向平面)时,杆件变形后的轴线将弯成一条位于外力作用平面内的曲线。这些定义都是从挠曲线与外力作用面的关系着手,给出了平面弯曲的特点,强调平面弯曲后梁的挠曲线仍为一条平面曲线。对于通常讨论的对称弯曲,要求横截面有对称轴,所有外载荷都作用于同一个纵向对称面内,如图1所示,力的作用面和梁的位移均位于纵向对称面内,故对称弯曲是一种特殊的平面弯曲。

图1 平面弯曲
如果外力不作用在纵向对称面内,梁在变形后的轴线将不再位于外力所在平面,这种弯曲称为斜弯曲[5]。教材[4]给出的斜弯曲定义为:载荷不作用在主轴平面内时所发生的弯曲称为斜弯曲。如图2所示矩形截面悬臂梁即发生了斜弯曲变形。这一定义以力和位移的方向是否一致进行判断,一致即为平面弯曲,不一致即为斜弯曲,判断方法形象直观,便于工程师应用。该定义适合于梁上受到同一方向横向载荷作用的情况,针对弯曲梁整体而言。

图2 斜弯曲
2 斜弯曲的第二种定义
如果横向载荷是作用在两个方向,以圆形截面梁为例,受力如图3所示,横向力分别作用在两个纵向对称面内,在两个载荷的相互作用下,力的作用方向与整体梁的位移方向是不一致的,按照第一种定义,该梁发生的应是斜弯曲变形。但是根据通常的理解,圆截面是不会发生斜弯曲变形的,这里给出平面弯曲和斜弯曲的第二种定义。教材[6]给出的定义为:当弯矩矢量平行于任一形心主轴时,中性轴平行于弯矩矢量,即中性轴垂直于弯矩的作用面,这种弯曲称为平面弯曲;当中性轴的方向与弯矩矢量的方向不同,或中性轴不垂直于弯矩的作用面,这种弯曲称为斜弯曲。该定义以中性轴方向与横截面上弯矩矢量的方向是否一致进行判断,一致即为平面弯曲,不一致即为斜弯曲,弯曲的类型是针对某一横截面的。通过简单计算即可判断,图3任一横截面上弯矩矢量方向和中性轴方向均一致,可见图3发生的是平面弯曲,横截面上任一点的正应力仍可按照平面弯曲正应力的公式进行计算。
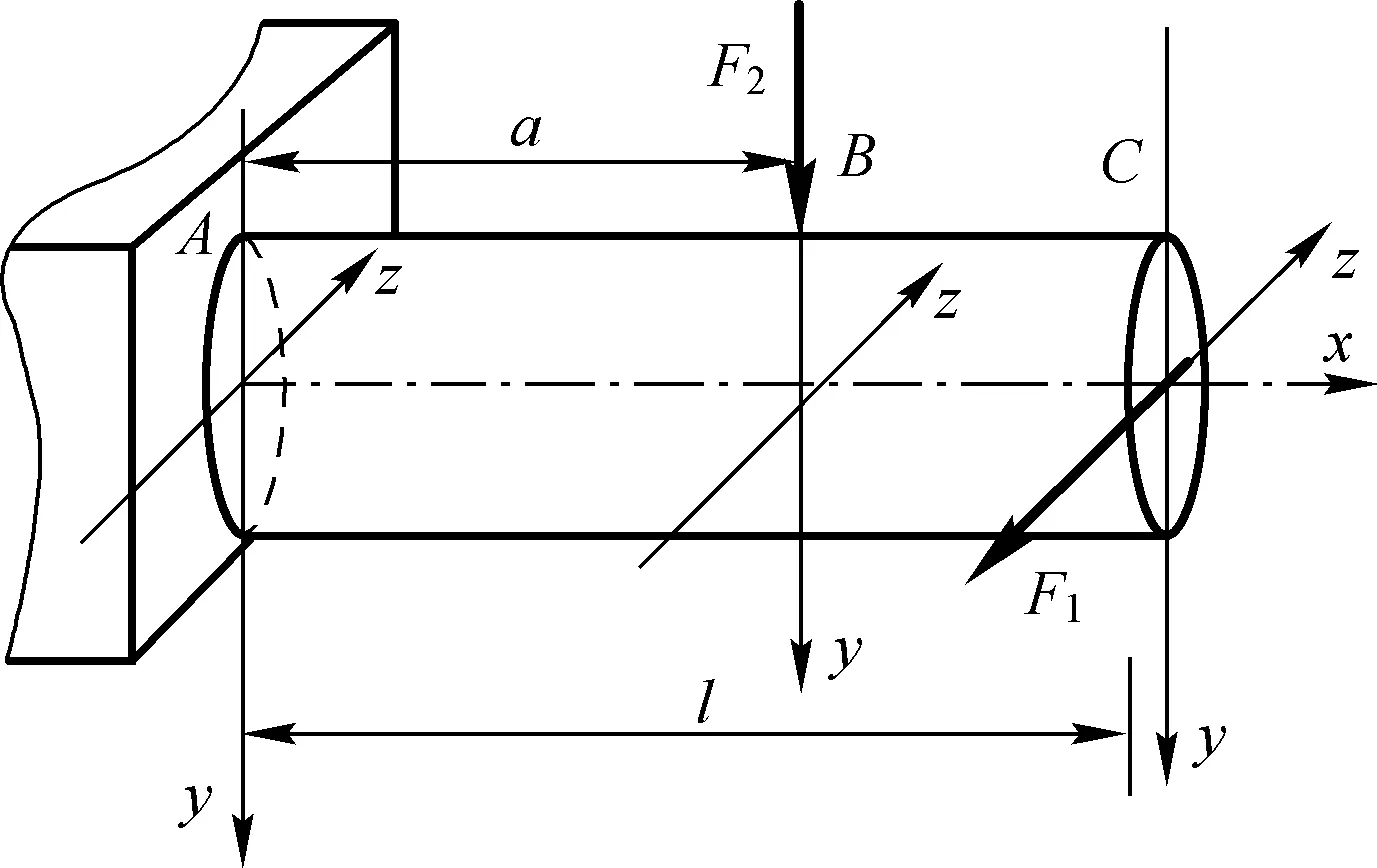
图3 圆形截面梁的弯曲

(1)
设该截面上中性轴与y轴的夹角为θ,则:
(2)
显然对于矩形截面Iy≠Iz,故θ≠φ,即中性轴的方向与弯矩矢量方向不一致,此时所发生的弯曲即为斜弯曲,正应力计算按两个方向的平面弯曲进行叠加。

图4 矩形截面梁的弯曲
3 斜弯曲情况下位移与中性轴的关系
众所周知,梁发生平面弯曲时,位移方向与载荷方向一致,与中性轴方向垂直。发生斜弯曲时,位移方向与载荷作用方向不再重合,这也是“斜”的本质,那么位移和中性轴之间是否还存在垂直关系呢?下面分两种情况进行简单定量分析。
图5所示矩形截面悬臂梁发生斜弯曲变形,设合成弯矩M与y轴的夹角为φ,该截面上中性轴与y轴的夹角为θ,则:
(3)

图5 矩形截面梁的斜弯曲
矩形截面Iy≠Iz,故θ≠φ。m-m横截面的形心沿z轴和y轴方向的挠度分别为:
(4)
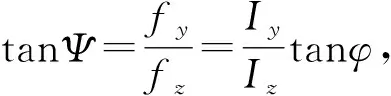
考虑图4的受力情况,AB段梁m-m横截面的形心沿z轴和y轴方向的挠度分别为:
(5)
设合成挠度与z轴的夹角为ψ,则:
(6)
对比式(2)和式(6),得到θ≠ψ,即该截面的位移与中性轴不是垂直的关系,教材[7-10]中讨论了同样的问题,指出此时挠度和中性轴是垂直的,这个结论是错误的。该情况下横截面中性轴和位移的方向会随着截面位置的变化而变化,挠曲线是一条空间曲线。
4 与工程实际的联系
工程设计中,强度和刚度问题是工程师们十分关心的问题。对于平面弯曲和斜弯曲,弯曲正应力和挠度的计算公式是不同的,工程师在分析一个具体弯曲问题时,首先要明确该问题的特点,其次依据不同的公式对问题进行强度和刚度分析。
以图5为例,假设矩形截面高宽比为3.3,外力偏离y轴5°,则弯曲平面与y轴的倾角约为44°,最大正应力较外力不倾斜时增大约30%。可见对于高而狭长的梁,由于对截面两个形心主轴的抗弯截面系数相差很大,使得外力稍有偏斜便会发生斜弯曲变形,从而引起很大的挠度,最大正应力也会显著增大,对梁的刚度和强度造成不利影响。例如吊车起吊重物时,如果吊车横梁为工字型截面或其它狭长截面,应尽可能地使起吊载荷沿截面的形心主惯性轴方向,避免因发生斜弯曲而产生过大的正应力和变形,造成不可挽回的损失。如果设计中采用箱型截面,从强度和刚度角度考虑就要比单一工字钢设计优越很多。
5 结论
(1) 本文讨论了经典教材中关于平面弯曲和斜弯曲的两种定义,一种定义考虑力的方向与位移方向是否一致,适用于梁上仅作用一个方向横向力的情况,形象直观,易于判断;另一种定义考虑横截面上弯矩矢量方向与中性轴方向是否一致,理论性稍强,但抓住了斜弯曲的本质。
(2) 所谓“斜”的含义,可以理解为弯曲变形不发生在外力作用面内,也可以理解为中性轴方向与弯矩矢量方向不再是同一个方向。
(3) 指出了教材[7-10]中的一处错误,梁发生斜弯曲时任一横截面形心的合成挠度方向不一定垂直于中性轴方向,需要根据具体的受力情况进行分析。
