基于狄拉克方程推导求解一维势垒问题
2022-05-25王怀玉
王怀玉
(清华大学 物理系, 北京 100084)
0 引言
在量子力学教科书中,薛定谔方程描述微观粒子的非相对论运动,克莱因-高登方程描述自旋为0粒子的相对论运动,狄拉克方程描述自旋1/2的粒子的相对论运动。
实际上,薛定谔方程是狄拉克方程的一个低动量近似[1-6]。而经典力学中,牛顿力学只是相对论力学的低动量近似。看上去,薛定谔方程和相对论量子力学方程的关系,与牛顿力学和相对论力学的关系一样。但是并不尽然。相对论量子力学方程比经典的狭义相对论力学至少多了一个内容:前者有负动能解。以狄拉克方程
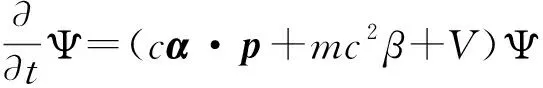
(1)
为例,这个方程在势能为零时的自由粒子的能量本征值为
(2)
有两支能量。一支是正动能的,一支是负动能。本文作者的研究表明[7],狄拉克方程除了正能解有低动量近似之外,负能解也应该有低动量近似。把这两个近似简捷回顾如下。
对于式(1)中的波函数做变换
Ψ=ψ(+)e-imc2t/ћ
(3)
式(3)代入式(1),然后做低动量近似,得到波函数ψ(+)满足的薛定谔方程[1-6]。
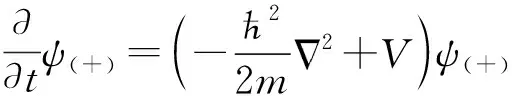
(4)
这个方程是狄拉克方程的正动能解的低动量近似,因此只适用于粒子的能量E大于势能V的区域。我们还可以做另一个变换[7],
Ψ=ψ(-)eimc2t/ћ
(5)
式(5)和(3)两个变换只是在指数上差一负号。式(5)代入式(1),然后做低动量近似,得到波函数ψ(-)满足的方程,
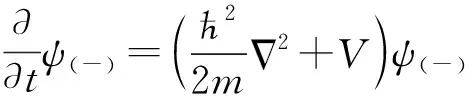
(6)
与薛定谔方程(4)相比,式(6)的动能算符有一负号,所以叫做负动能薛定谔方程。它是狄拉克方程的负动能解的低动量近似,因此,只适用于粒子的能量E小于势能V的区域。我们将两个低动量方程及其使用范围列于表1。

表1 量子力学的两个低动量方程. E表示粒子的能量
我们回顾狭义相对论创立的年代,如果不是从狭义相对论公式做低速近似,谁也不会知道牛顿公式只适用于低速运动。因为从牛顿公式本身,是看不出这一点的。现在,如果不是从相对论量子力学方程做低动量近似,谁也不会知道应该还有一个负动能低动量方程。因为从薛定谔方程本身,是看不出这一点的。
众所周知,在到目前为止的经典力学中,动能只可能是正的,不可能是负的。在量子力学的薛定谔方程在E>V的情况,是有经典对应的。人们发现,在粒子的能量E小于势能V,E 可是,作者指出[7],薛定谔方程在势垒区域是否适用,既没有实验上的定量验证,也没有理论上的严格推导。通过以上式(5)和(6)的步骤,作者从理论上严格推导出了负动能薛定谔方程。并且论证薛定谔方程和负动能薛定谔方程的适用范围,如表1所示。 薛定谔方程和负动能薛定谔方程结合成一对方程,使得相对论量子力学方程关于正负动能解的三个对称性在低动量运动得以保留[7]。第一个是正负动能解的对称性,如式(2)所示。第二个是正负动能解的流密度数值相同方向相反。第三个是如果势能取相反数,则方程的本征值取相反数,正负动能解交换。作为相对论量子力学方程的一个低动量近似的薛定谔方程则没有这三个对称性。可知,薛定谔方程有缺陷。而负动能薛定谔方程的出现,弥补了这个缺陷。 由此,作者认为,量子力学的负动能解与正动能解应该具有完全同等的地位。据此,作者圆满解决了一个相对论粒子遇到势垒时的克莱因佯谬[8]。作者还研究了负动能态的占据的问题[9]和负动能物质的运动方程[10]。作者还建议实验来验证负动能电子[7]。事实上,关于正负动能的对称性是自然界中广泛存在的,作者对于维里定理的研究[11]表明了这一点。 到目前为止,量子力学教科书上求解的势垒问题都是使用薛定谔方程。我们现在已经证明,薛定谔方程只适用于正动能的区域,而对于负动能的区域,必须使用负动能薛定谔方程。既然如此,以往的势垒问题都必须在新的观点下进行考察。本文重新求解了量子力学上几个常见的势垒问题,得到的结果与量子力学教科书有所不同。本文只考虑定态问题。 一维有限深方势阱为 (7) 设粒子的能量为E,并且我们只考虑如下的能量范围: 0 (8) 我们分三个区写出粒子的波函数所满足的方程。由能量与势能的关系可知,在x<0的区域I和x>a的区域III,粒子的动能是正负的,应服从负动能薛定谔方程;在0≤x≤a的区域II,粒子的动能是正的,应服从薛定谔方程。由此,这三个势能区域的波函数满足的方程和能量动量关系应如下。 (9a) (9b) (9c) 其中所有的动量都是正数。容易看到,每个区域内的波函数都是平面波的叠加。 我们设:在左右两侧,没有粒子从无穷远处入射。因此,在区域I,只有从右向左的波,在区域III,只有从左向右的波。先尝试把三个区域中粒子的波函数写成如下形式。 ψI=B1e-iq1x/ћ (10a) ψII=A1eipx/ћ+A2e-ipx/ћ (10b) ψIII=B2eiq2x/ћ (10c) 在边界x=0和x=a处,波函数连续的条件是 B1=A1+A2 (11a) A1eipa/ћ+A2e-ipa/ћ=B2eiq2a/ћ (11b) 波函数导数连续的条件是 -q1B1=p(A1-A2) (12a) p(A1eipa/ћ-A2e-ipa/ћ)=q2B2eiq2a/ћ (12b) 由此四式解得系数有非零解的条件是 -2p(q1+q2)cos(pa/ћ)+2i(p2+q1q2)sin(pa/ћ)=0 (13) 由于动量都是正数,式(13)要求实部和虚部都为零。先看虚部。注意,q1=-q2=p是不可能的,因为从式(10c)知-q2表示第III区域的波是从左往右的,这意味着右侧会有粒子从外入射而没有出射,与我们上面的假设矛盾。因此虚部只能要求 sin(pa/ћ)=0 (14) 在这个前提下,式(13)实部为零的条件是 q1=q2=0 (15) 将式(15)代入(12),则得不到非零解。说明式(11)和(12)写得不正确。而此两式来源于波函数的形式(10)式。 由式(15)可知,在区域I和III实际上并没有平面波。因此,这两个区域的波函数为零。可见,尝试波函数(10)写得不对,应写成 x<0:ψI=0 (16a) 0≤x≤a:ψII=A1eipx/ћ+A2e-ipx/ћ (16b) x>a:ψIII=0 (16c) 如此,只有波函数在边界上连续的条件,就是式(11)。并且其中 B1=B2=0 (17) 由此得到式(14)。最后得到势阱中波函数为 (18) 并且由式(14)有 (19) 粒子的能量就是 (20) 可见,有限深势阱中的波函数和能级与无限深势阱中的情况完全相同。只是有限势阱中的束缚态能级有一个上限V1,由式(8)所决定。 我们这一结果显然与量子力学教科书上的结果不同[4-6,12-14]。这是因为,虽然现在两侧的势垒是有限高的,但是无限宽的。在势垒中也是平面波。既然粒子是局域在势阱中,且没有粒子从无限远处入射,势垒区域的波函数就只能为0,所以,波函数只能存在于阱内的区域。 由于本文的结果与教科书上的结果有区别,作者在此做一点评述。在参考文献[7]中,作者指出,教科书上对于势垒穿透模型,既没有实验上的定量验证,也没有理论上的严格推导。本文以上结果,也只是理想模型。这个模型没有实验上的定量验证。但是,在势垒区域的方程是从狄拉克方程推导得到的,理论上是严格的。因此,本文的结果理论上是合理的。 本题用三维球坐标。设势阱是 (21) 也可以称为球形势阱。我们考虑的粒子的能量范围是 -V0 (22) 粒子在r≤a的区域具有正动能,在r>a的区域具有负动能。径向函数R(r)在两个区域满足的正负薛定谔方程如下。 (23) (24) 这两个都是球贝塞尔方程,解是整数阶球贝塞尔函数[15]。考虑到边界条件,在正负动能区域的解分别用第一类球贝塞尔函数和第一类球汉克尔函数。 r≤a:R(r)=Ajl(κ1r) (25) r>a:R(r)=Bhl(κ2r) (26) 在势阱边界用边界条件。 Ajl(κ1a)=Bhl(κ2a),Aj′l(κ1a)=Bh′l(κ2a) (27) 系数有非零解的条件是 (28) 利用贝塞尔函数之间的关系式[15]可计算得式(28)左边的行列式,因结果较繁,就不写在这儿了,不过,它不为零。这就是说,式(28)实际上不能满足的。这说明,在负动能区域所设的波函数(26)不正确。在负动能区域的波函数只能为零。所以,波函数只能取以下形式: R(r)=Ajl(κ1r)θ(a-r) (29) 其中,A是归一化系数,κ1的取值满足边界条件 jl(κ1ia)=0,i=1,2,… (30) 束缚态能级的上限由式(22)决定。 为清楚起见,我们来看最简单的情况。对于l=0的s态, (31) 若解是式(25)和(26),由这两个函数计算式(22)的行列式,必须满足下列条件。 κ2sin(κ1a)+iκ1cos(κ1a)=0 (32) 式(32)无解。这说明,式(26)的波函数不正确。波函数只能写成式(29)的形式,即负动能区域的波函数只能为零。本征值则由边界条件(30)决定。 本题与1.1小节中的一维有限深势阱的情况类似,虽然势垒区域有限高,但是无限宽。没有粒子从无限远处入射。所以势垒区的波函数只能为零。 按照教科书[2,4,5,6,13],由于在势垒区域也是用薛定谔方程,势垒区域中有指数衰减的波函数。可是这样的认识不正确的。原因如下。 当粒子做相对论运动的时候,由于正负能谱之间有2mc2的能隙,例如,自由粒子的式(1)就是如此。粒子不能在这个能隙内运动。因此,在这个能隙内,粒子的动量是虚数,波函数是指数式的[8]。当粒子做低动量运动时,能量动量关系不是式(1)这样的形式,能量动量关系中没有这样的能隙。因此,粒子的动量不会是虚数。 本题用球坐标。球方势垒是指如下的势能。 (33) 我们考虑的粒子能量的范围是 0 (34) 这个问题也属于低能散射的一个问题。粒子在r>a的区域具有正动能,在r≤a的区域具有负动能。径向函数R(r)在两个区域满足的正负薛定谔方程如下。 (35) (36) 这两个都是球贝塞尔方程,解是整数阶球贝塞尔函数。将两个区域的解写成如下形式, r≤a:R(r)=jl(κ1r) (37) r>a:R(r)=Ajl(κ2r)+Byl(κ2r) (38) 利用边界条件,解得系数的表达式为 (39) 能量可以是连续谱。 我们来看最简单的情况。对于l=0的s态,球贝塞尔函数为 (40) 可以求解出系数A和B,只是表达式较繁。径向波函数就是 (41a) (41b) 我们把这儿的结果与量子力学教科书上的结果[1,2,4,13]稍做比较。那儿对于l=0的s态写出的波函数是 (42a) (42b) 比较本文的结果(41)式和教科书上的结果(42)式可知,在势垒外的波函数的形式相同,在势垒内的波函数的形式有区别:分子上分别是正弦函数和双曲正切函数,κ1↔iκ1。这一差别是由于在势垒内部分别使用负动能薛定谔方程和薛定谔方程造成的。由于势垒内部波函数的差别,在r=a的边界处的连接条件导致式(41b)和(42b)中的系数有所不同。不过,当势垒的半径趋于零,a→0,式(41)和(42)趋于完全相同。 一个粒子受到一个常力F的作用,它的势能是 V(x)=-Fx (43) 教科书[2,5,13,14]上对此问题有标准的解法。就是求解如下的薛定谔方程: (44) 得到的解是Airy函数。 我们来比较粒子的能量和势能。容易看到:当x>-E/F,E>-Fx,动能是正的;当x<-E/F时,E<-Fx,动能是负的。因此,在这两个区域,粒子应分别满足薛定谔方程和负动能薛定谔方程。 (45a) (45b) 令 (46) 则方程(45)变换成如下形式。 (47a) (47b) 式(47b)中做变量代换ζ=-ξ后,可成为和(47a)一样的形式。因此,式(47)也可以统一地写成一个方程: (48) (49) 右边是两个线性无关解的线性组合。它们实际上是±1/3阶贝塞尔函数J±1/3。利用这个贝塞尔函数J±1/3,可把式(49)写成更为紧凑的形式: (50) 这是在区域ξ>0的解。类似地,在区域ξ<0的解应该是 (51) 在ξ=0处,波函数及其导数连续。我们就得到 B2=B1,A2=-A1 (52) 此二式还不足以定四个系数,因为还只用到了一个边界的条件。另外还有在无限远处的边界条件。无限远处,可以用贝塞尔函数的渐近形式[15]。 (53) 注意到统一的方程(48)具有一定的对称性。它就应该有对称或者反对称解。因此,两个区域的波函数的振幅就应该相等。所以只可能有两种选择:一个是A1=0,这是对称解;另一个是B1=0,这是反对称解。 由于使用了负动能薛定谔方程,我们得到的解与量子力学书上教科书[2,5,13,14]上的结果Airy函数是不同的。在此想说明一点。势能函数(43)具有一定程度的左右对称性:以能量等于势能点为界,势能相当于是关于此点左右反对称的。相应地,方程应具有式(48)所显示的对称性。由于势能和方程具有这样的对称性,我们期望解也是有一定的对称性。我们此处的解确实有左右对称或者反对称的 。而教科书上,在这种势能时求得的解是Airy函数,完全没有左右对称性。我们认为,相比之下,此处的解在物理上更为合理一些。 Kronig-Penney模型[13,16]的势能是 (54) 这是一个周期势场。把V(x)=0的区间称为势阱区间,V(x)=V0的区间称为势垒区间。我们考虑的粒子能量范围是 0 (55) 因此,粒子在势阱区间具有正动能,应遵从薛定谔方程;而在势垒区间具有负动能,应服从负动能薛定谔方程。 分别写出势阱和势垒区间的方程与能量动量关系如下。 (56) (57) 已知薛定谔方程中的势能如果是周期的,方程的解就是布洛赫波[4,5,12,16]。现在波函数在不同区域分别遵循不同的方程(56)和(57),它是否仍然具有布洛赫波的性质?答案是肯定的。这一点容易证明。 我们可以把式(56)和(57)合并成如下形式: (58) 这是一个薛定谔方程,其中的势能是如下的“周期势”。 (59) 所以,由式(56)和(57)求出的波函数确实是布洛赫波。 满足式(56)和(57)的波函数应该都是平面波的线性叠加。 ψI=Aeiqx+Be-iqx (60) ψII=Ceipx+De-ipx (61) 在边界处,波函数及其导数连续。再加上一个布洛赫定理。即可得到式(60)和(61)有非零解的条件是 pq+pqei2Kc+[(p2+q2)sin(qa)sin(pb)- 2pqcos(qa)cos(pb)]eiKc=0 (62) 其中K是倒格矢。粗一看,式(62)似乎含有两式:实部和虚部各有一式。实际上,这两式刚好是一样的: (63) 这一结果可以与教科书[13,16]中的结果做比较。这一结果与教科书上的结果的差别是:将此处的p代之以ip就可以得到教科书[13,16]中的结果。 当所有势垒区的宽度趋于0,高度趋于无限大,就是狄拉克梳。我们来取这个极限。 b→0,pb→0,p≫q (64) 令 p2ab/2=P (65) 是个常数。那么可以得到 (66) 这就是狄拉克梳的结果[4,5,12,13,16]。 此处的结果与教科书上的结果的差别是:教科书上,在势垒区间的波函数是指数波,本文的是平面波。但是在势垒宽度趋于零时,两者趋于相同的结果,即(66)式。这说明势垒区越窄,这两者的差别越小。这在物理上也是容易理解的。势垒区间越宽,指数波的变化越大。 我们来考虑固体中的情况。在格点上是离子实,离子实之间因相互作用而形成稳定的结构。价电子在固体内运动。靠近离子实的区域,是势阱,价电子应该具有正动能;在离子实之间的区域,应该有势垒。对于金属而言,势垒应该是比较低的。所以金属中的电子可以看做是近似自由的。对于其它情况,势垒就相对比较高。势垒区域内的电子应该具有负动能。现在计算固体电子结构的第一性原理程序,除了考虑相对论效应之外,都是使用薛定谔方程。按照作者的观点,在势垒区域是需要应用负动能薛定谔方程的。那么,在势垒区域,是平面波的叠加而不是指数波的叠加。由于势垒区域的宽度是非常窄的,在绝大多数情况下势垒内部的指数波与平面波的差别可以忽略不计。但是也可能在某些情况下这样的差别会有一定的影响。目前的第一性原理计算程序对于材料的电子结构的描述非常好。但还是有一点的表现不是令人满意的:对于有些材料计算声子谱的时候,在布里渊区中心点附近会计算出负频率,其原因未知。如果公式推导正确和编写程序无误,不应该出现负频率这样的结果。有的文献用引入多声子的高阶项的办法,来得到负频率消失的结果,但是这个办法的正确性是需要探究的。作者的建议是在势垒区域运用负动能薛定谔方程做计算,以期有所帮助。 假设势能的变化缓慢,粒子运动在正负动能的区域之间。那么,在正负动能变化的那一点,称为转折点,在粒子的动量较低时,有WKB近似法[17-19]。 先看正动能区的情况。粒子服从薛定谔方程。 (67) 令波函数的形式为 ψ(+)(x)=eiS(+)(x)/ћ (68) 代入(67)式。并将S(+)(x)按照普朗克常数ћ作为小量展开。 (69) 然后,按照ћ的同次幂的系数之和为零,我们就可写出分别写出ћ的零次幂、一次幂和二次幂的系数的方程。 (70) S″(+)0+2S′(+)0S′(+)1=0 (71) (S′(+)1)2+S″(+)1+2S′(+)0S′(+)2=0 (72) 其中,丛零次项的系数方程(70)容易求的S(+)(x)的零级项S(+)0为 (73) (74) 那么,波函数(68)式的指数上准确到一级项为 (75) 对于负动能的区域,做同样的处理。负动能薛定谔方程为 (76) 令波函数的形式是 ψ(-)(x)=eiS(-)(x)/ћ (77) 代入式(76)。并将S(-)(x)如式(69)那样按照普朗克常数ћ作为小量展开。然后,按照ћ的同次幂的系数之和为零,我们就可写出分别写出ћ的零次幂、一次幂和二次幂的系数的方程。 (78) S″(-)0+2S′(-)0S′(-)1=0 (79) (S′(-)1)2+S″(-)1+2S′(-)0S′(-)2=0 (80) 从零次项的方程(78)得到零级项S(-)0的表达式, (81) 代入(79)式,得到一级项是 (82) 这时的波函数(77)式的指数上准确到一级的表达式为 (83) 以上近似的适用条件是 (84) 但是在转折点附近,由于动量为零,这一条件不满足。就需要有一个连接条件。 我们来探索WKB连接公式。 看图1势垒形状的情况。 图1 势垒区域 考虑转折点a邻近的情况。当x V(x)=V(a)+V′(a)(x-a)=E-F0y (85) 其中 y=x-a,F0=-V′(a)>0 (86) 将(85)式在x (87) (88) 引进无量纲变量。 (89) 那么,式(87)和(88)简化为 (90) (91) 此两式的形式与(47)相同。所以解为 ±1/3阶贝塞尔函数的线性叠加。 (92) (93) 利用在ξ=0处连续且光滑的条件,得到 A1=-B1,A2=B2 (94) 在离转折点较远处,可以利用贝塞尔函数的渐进式(53)。 (95) (96) 在转折点a点的两侧邻近,当x (97) 当x>a。已经由(81)式定义了p。由式(85)、(86)和(89)可知, (98) 将式(97)和(98)分别代入式(95)和(96),转折点两侧的波函数可以写成 (99) (100) 它们分别和式(75)与(83)是一样的,并且把该两式中的相位常数α和β定出来了。这儿要注意的是,如果相位常数相同,那么,转折点两侧的函数一个是正弦形式,另一个是余弦形式。 同理,在转折点b处两侧的波函数为 (101) (102) 此处在转折点两侧,都是三角波,都有一个相位常数。而文献上,在势垒区域,是指数波。指数波是没有相位的概念的。 现在将以上讨论的WKB近似的波函数形式应用到势垒区域的透射和势阱区域的波函数两种情况。 我们考虑势垒穿透的问题。由于我们只做定性的讨论,采用文献[5]所用简化版本。这个简化版本如下。 设在x<0的第I和x>a的第III两个区域,势能为零。有一个正动能粒子从左侧无限远处往右运动。那么,在第I区域有入射波和反射波,在第III区域则有透射波。这两个区域的波函数如下。 x<0:ψI(x)=eiqx/ћ+Be-iqx/ћ (103) x>a:ψIII(x)=Geiqx/ћ (104) 这两个区域的能量动量关系都是 E=q2/2m (105) 在0≤x≤a的区域则是粒子的能量小于势能的势垒区,E (106) 注意此式只在T≪1时适用。 说以上模型是个简化版本,是因为实际上第I和第III两个区域的势能可能不为零。但是,这两个区域的势能V(x)是小于能量的,计算得到的透射系数还是式(106)[1,5,20]。因此,采用简化版本不带来实质性的差别。 我们用此简化版本,就是在第I和第III区域,波函数就用式(103)和(104)。在势垒区域,则依据前面的讨论,波函数应该写成 (107) 其中 (108) 我们强调,在势垒区域的波不是指数波。在x=0和x=a处的边界条件是以下各式。 (109a) (109b) (109c) (109d) 其中, (109e) 由边界条件(109)式解出四个系数。其中反射振幅B的表达式为 (110) 反射系数是 (111) 这时的势垒穿透系数并不是如式(106)那样随势垒宽度指数下降的。而是随着角度γ周期性变化的。这是我们的结果与教科书上的结果比较实质性的差别。而且式(111)对于任意势垒宽度都适用,不像式(106)那样只对很小的透射率也就是较宽的势垒适用。 我们再来看势阱区域的情况。 这种情况是指:在x<0的第I和x>a的第III两个区域,势能大于粒子的能量。而在0≤x≤a的区域,粒子的能量大于势能。假设,没有粒子从远处入射。那么,依据前面的讨论,我们可以设三个区域的波函数如下。 (112) (113) (114) 在x=0和x=a处的边界条件是以下各式。 (115a) (115b) (115c) (115d) 其中,γ的形式与式(109e)同。当我们用(115)求解四个系数时,发现无解。究其原因,是因为我们设了第I和第III两个的区域的波函数不为零,是式(111)和(113)这样的形式。实际上,这两个区域的波函数应该为零。即 x<0:ψI(x)=0;x>a:ψIII(x)=0 (116) 而边界条件就简化为两个:在两处边界波函数为零。 C1+C2=0 (117a) C1eiγ-C2e-iγ=0 (117b) 这种情况与1.1小节中的相同。也是因为两侧的势垒是无穷宽的,又没有粒子从远处入射而来,所以势垒区域的波函数必须为零。 (1) 本文计算了常见的一维势垒问题,它们是:一维有限深方势阱,三维有限深方势阱,三维有限深方势垒,一维线性势,Kronig-Penney模型,WKB近似方法。量子力学教科书上在求解这些问题的时候,不区分粒子的能量和势能的关系,在所有区域统一使用薛定谔方程。作者强调,薛定谔方程在粒子能量小于势能的区域是否适用,并没有任何论证。作者根据表1,重新求解了这些问题,在粒子能量小于势能的区域使用负动能薛定谔方程。所得到的结果与教科书上的有所不同。 (2) 本文的结果与教科书上结果不同之处如下:1.1、1.2和1.6小节表明,有限高的势垒,只要是无限宽的,那么,在势垒内部,本文给出的波函数为零,而教科书上是有指数波的尾巴。我们说明了低动量运动时,粒子的动量不会是虚数。1.3、1.5和1.6小节的内容表明,在有限高有限宽的势垒内部,本文给出的是正反向平面波的叠加,而教科书上则是指数波。1.3和1.5小节表明,势垒宽度越窄,本文与教科书上的结果越接近。对于δ型势垒,两者的结果是一样的。1.4小节的线性势本身具有一定的对称性,我们解得的波函数确实体现了对称性。而教科书上的波函数解是Airy函数,则没有这样对称性。1.6小节的例子表明,势垒的透射系数是随着势垒宽度变换,会有某种周期性的变化,而教科书上透射系数是随着势垒宽度指数衰减的。 (3) 文中给出的势垒问题都是模型,还没有在实验上给出定量验证。期待下阶段通过实验物理给出验证。1 几个一维势垒问题的重新求解
1.1 一维有限深方势阱
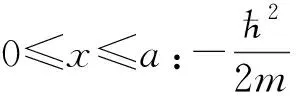
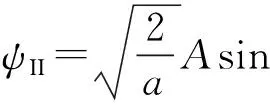
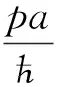
1.2 三维有限深方势阱
1.3 三维有限高球形势垒
1.4 一维线性势
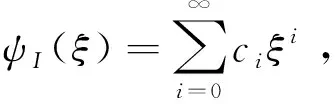
1.5 Kronig-Penney模型
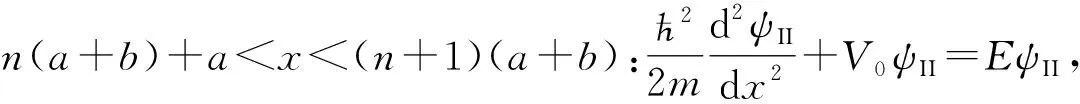
1.6 WKB近似

2 结论
