机载双基地协同探测雷达杂波模型分析

徐 晋，周德兵，朱 伟，郁 文，徐 岳

（1.中国电子科技集团第三十八研究所，安徽合肥 230088；2.上海机电工程研究所，上海 201109）

0 引言

由于战场电磁环境日益复杂，隐身战机的使用更加频繁，机载单基地雷达自身容易暴露目标、生存能力差的缺点愈发暴露。为了实现增程探测和对重要目标的保护，机载双基地雷达通常为一发一收或者一发多收，发射雷达采用大型预警机，接收雷达使用小型无人机进行前置探测。前置的接收机具有较好的隐蔽性和较强的生存能力。机载双基地雷达兼具机载单基地雷达和双基地雷达的特点，因此，其杂波空时特性较复杂，杂波建模较难。

在机载双基地雷达杂波特性研究方面，文献［2］建立了几类特殊双基场景的几何模型；文献［3］构建了地面固定坐标系，然后建立了一个时不变固定坐标系中的杂波数学模型；文献［4-5］分析了机载双基雷达杂波分布在传统的二维模型下存在的距离依赖性问题；文献［6］分析了机载双基雷达的距离特性；文献［7］给出了一种正侧视阵机载雷达系统杂波信号模型；文献［8-9］分析了机载双基雷达杂波空时分布特性和杂波的非平稳性。

本文在机载双基地雷达杂波研究的基础上，分析了机载双基地雷达杂波空时分布特性；针对机载双基地雷达的几何关系，充分考虑了双基地接收波束和发射波束指向的关系等因素，对地面反射模型中的参数进行优化，该模型比传统机载雷达杂波模型更精确；最后对双机不同姿态配置方式下的空时二维杂波谱进行了仿真。

1 机载双基地雷达杂波空时分布特性

与机载单基地雷达杂波分布相比，机载双基地雷达既要考虑机载雷达杂波的距离环特性，也要考虑发射平台和接收平台的运动特性和姿态特性，与双机的姿态、航向等运动特性都有关系。该过程中的因素和变量较多，使得双基杂波分布非常复杂，杂波特性会随着双机部署场景的不同而发生变化。无论机载雷达阵面在何种朝向，杂波分布均存在严重的距离依赖性。在单基情况下，等距离环均为以雷达为中心的圆环，一个距离单元处的俯仰角始终不变。但在双基情况下，发射机和接收机的分离使得等距离环表现为不规则椭圆，这意味着在一个距离单元处的俯仰角不再是固定不变的，而会随方位角的变化而变化。

为了方便分析机载双基地协同探测雷达杂波空时分布特性，将接收阵面中心在地面上的投影点作为坐标原点，将双基地基线在地面的投影作为轴，建立直角坐标系，任意几何关系下的机载双基地雷达示意图如图1所示。

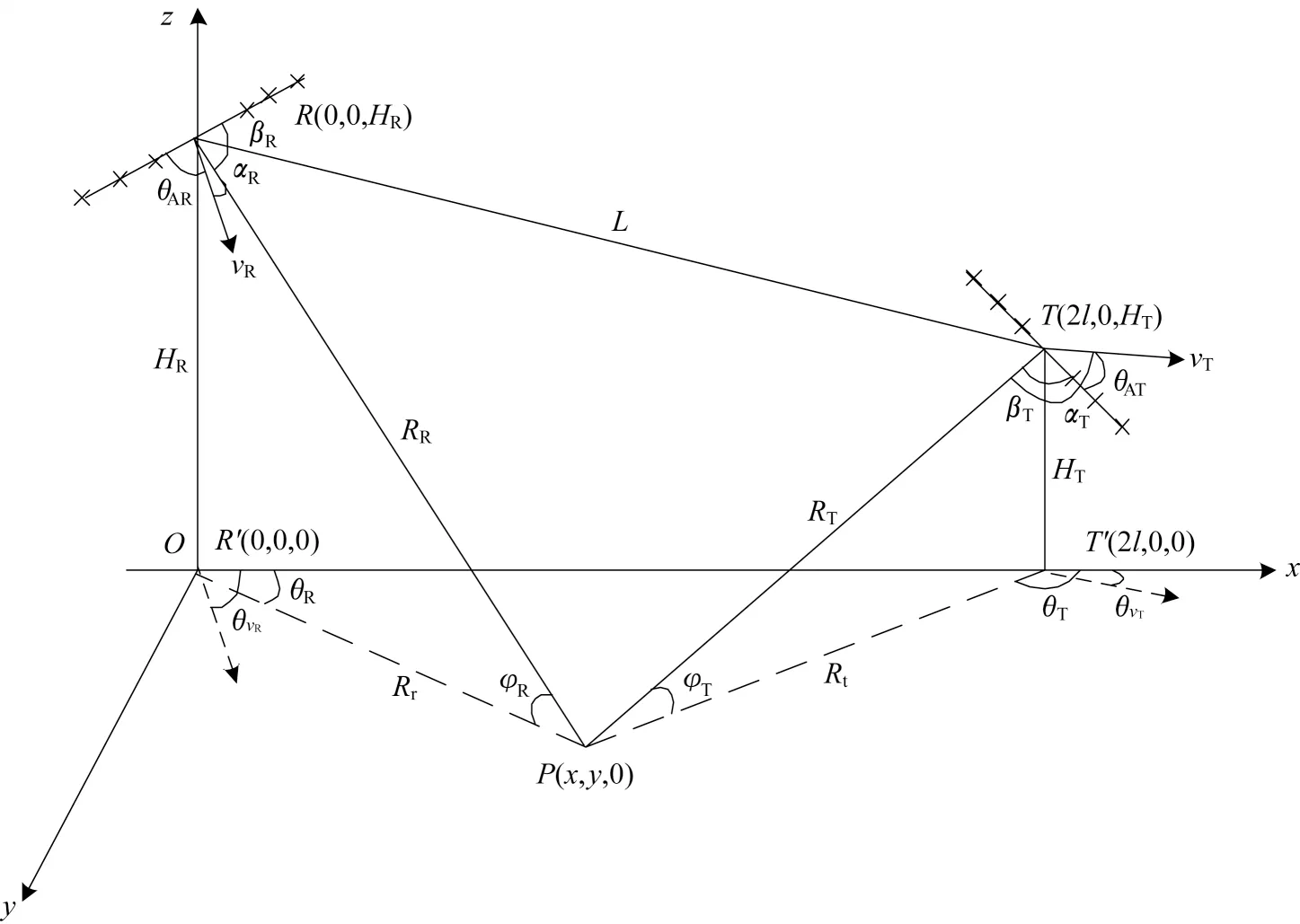
图1 机载双基地协同探测雷达几何关系Fig.1 The geometric relationship of airborne bistatic cooperative detection radar

图中：和分别为发射机和接收机的高度；和为发射机和接收机的速度；接收机天线采用二维面阵，点为某一距离单元的一个目标散射点；和分别为发射机和接收机的视线方向与水平天线阵方向的夹角；和分别为发射机和接收机的视线方向与载机运动方向的夹角（空间锥角）；为接收机运动方向与天线阵方向的夹角，前视模式时=90°；θ和θ分别为发射机和接收机载机飞行方向相对于基线方向的方位角；和分别为目标离发射机和接收机载机的距离；和分别为目标离发射机和接收机载机地面投影的距离；和分别为发射机和接收机载机的俯仰角度。

由此可写出多普勒频率、水平空间频率和垂直空间频率三者的表达式如下：

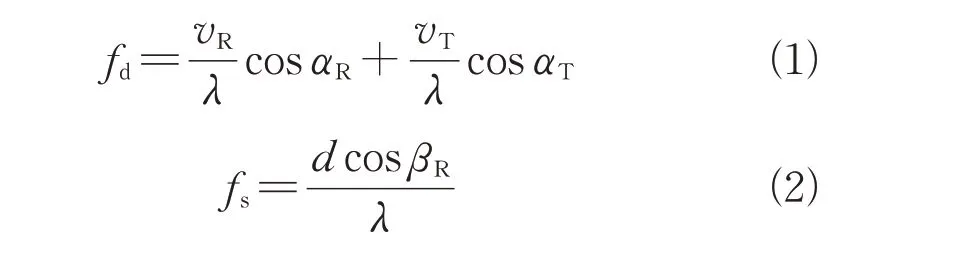
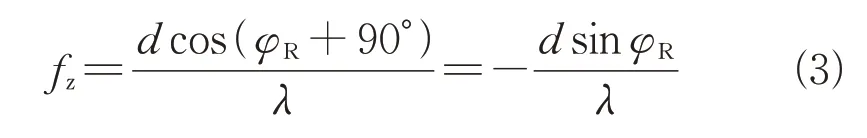
式中：为波长；为阵列天线相邻阵元之间的间距。

由机载双基地雷达几何关系可知，目标相对接收机的俯仰角和方位角分别为

雷达接收机和目标散射点在地平面的投影距离可以表示为

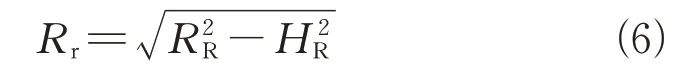
雷达发射机和目标散射点的距离为

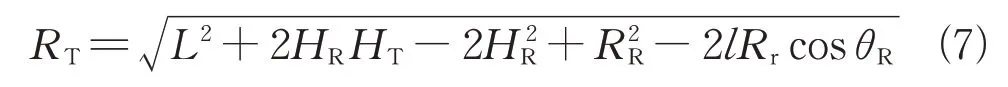
雷达接收机和雷达发射机在地平面投影距离的一半为

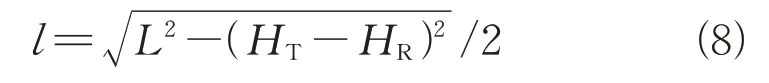
目标散射点相对雷达发射机的方位角为，其三角函数关系可以表示为

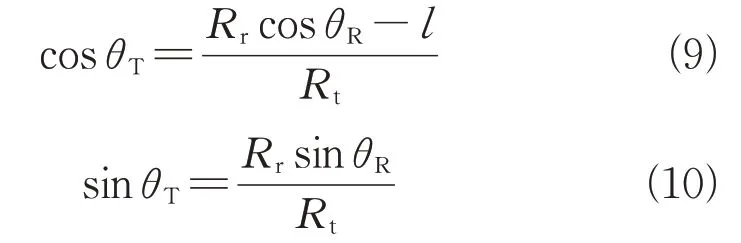
垂直空间频率可以表示为

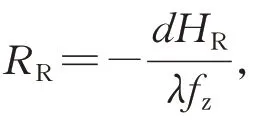
由于θ和为常数，和为的函数，可得为和的函数，即为和的函数，记作=(，)。

同样由空间角关系，多普勒频率f可推导如下：

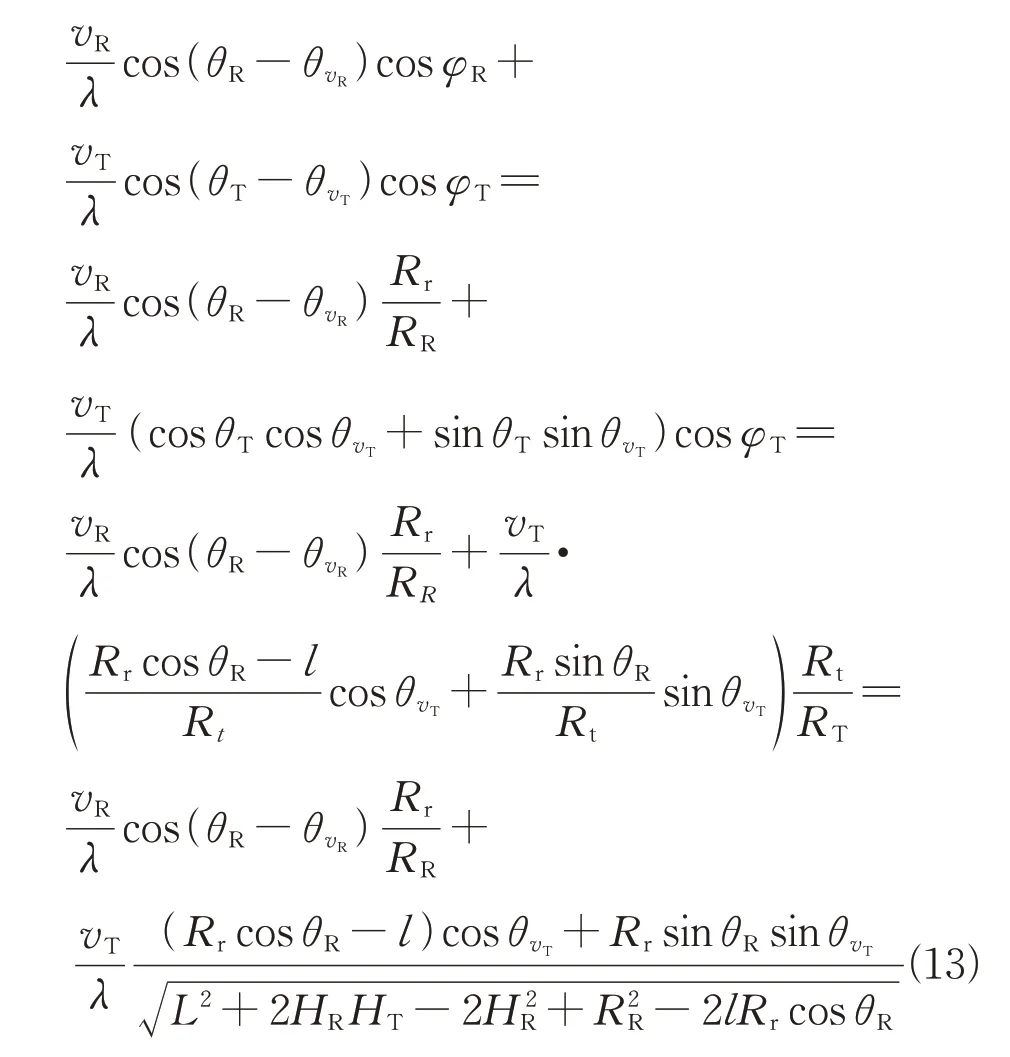
可见结果表达式中除去常数外，只与、和有关，而、和均与和有对应的函数，故可表示为=(，)，即3 个频率之间存在函数关系，表明不同距离单元杂波在三维空间处于同一曲面。

2 机载双基地雷达杂波模型

根据机载双基地协同探测雷达的几何关系和杂波空时特性，对传统机载雷达杂波模型进行优化，将地面反射的Morchin模型修改为

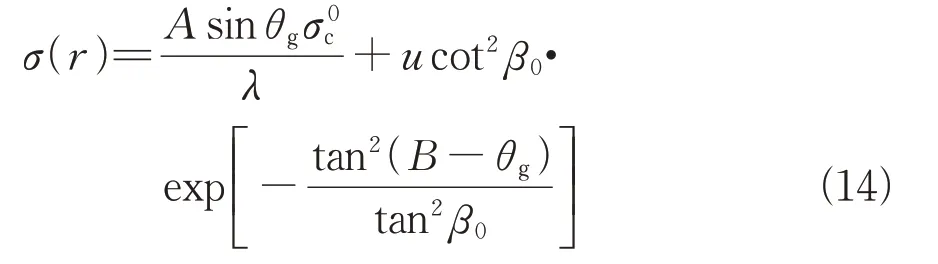
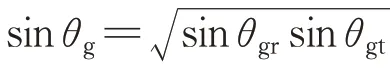
假设接收阵接收通道为，脉冲个数为，杂波距离环个数为，以C(，)表示第个接收通道的第个脉冲对第个距离环的杂波数据，考虑等效阵元方向性及距离调制，有

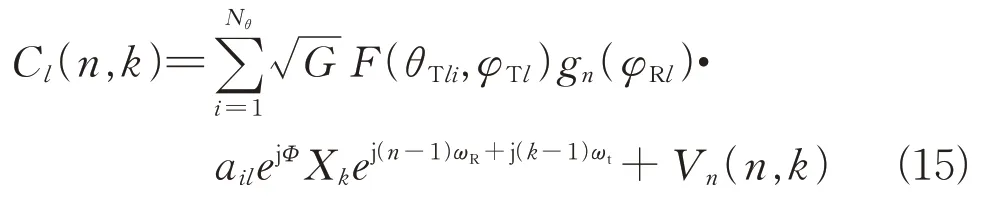
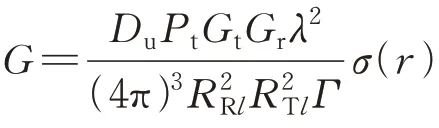
用×1维矢量表示空时二维杂波样本：

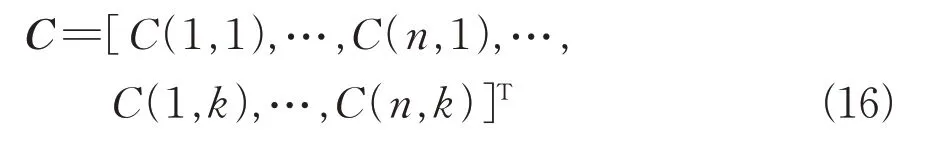
则杂波协方差矩阵为

3 计算机仿真分析

3.1 机载双基地协同探测雷达杂波空时分布特性仿真

首先对机载双基地协同探测雷达的杂波空时分布特性进行仿真分析。由于双基地部署，其接收机和发射机之间独立运动，会产生多种可能的几何场景。在此假设发射机天线和接收机天线均为正侧面放置，由于双机飞行姿态的关系，双机协同探测考虑以下6种姿态配置方式，如图2所示。

图2 双机飞行姿态配置模式Fig.2 Configuration mode of double airplanes flight attitude

其中，模式1 为一前一后的双机模式，模式5 为一左一右的双机模式，属于典型的双机配置模式，其余模式为不同程度的交错双机模式。为了分析方便，图2中的所有倾斜角度均为45°的整数倍。

仿真参数为：双基机载的发射机和接收机飞行速度分别为=200 m/s 和=200 m/s，双基载机的基线距离为=100 km，发射机和接收机的飞行高度分别为=10 km 和=8 km，雷达脉冲重复周期为=1/=1 ms，雷达工作频率=515 MHz，雷达波长为=0.58 m。对于上述6 种经典的机载双基配置模式，杂波位于不同双基地距离和（130 km、250 km、270 km、600 km）时，其杂波空时分布特性仿真结果图3所示。

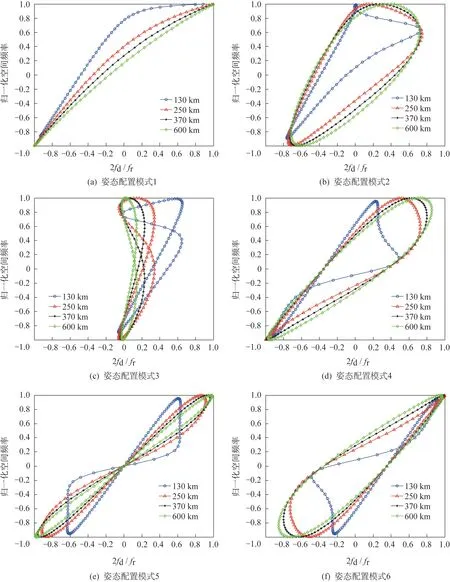
图3 不同姿态配置模式下的杂波空时分布特性Fig.3 Space-time distribution of clutter under different attitude configuration modes

从上面6 种姿态配置模式下的杂波空时分布特性可以看出：杂波空时分布特性与单基地杂波有较大差异，杂波谱空时分布与双机的相对姿态及飞行方向均有关系。当双基地距离和与基线距离比较接近时，杂波谱空时分布变化剧烈；当双基地距离和远大于基线距离时，杂波谱空时分布变化渐渐趋于平缓。

3.2 机载双基地协同探测雷达二维杂波谱仿真

对机载双基地协同探测雷达的二维杂波谱进行仿真分析。仿真参数为：假定雷达的有效接收功率密度是一个归一化的常量因子，即=1，发射主波束指向(，)=(30°，2°)，收发天线阵行数为8，列数为16，相干处理脉冲数为64，距离环个数为128，双基地距离和为250 km，反射面为丘陵，幅度分布统计模型为瑞利分布，其余参数设置同3.1 节。对上述双基配置模式中的模式1 和5（典型双机并行飞行场景）进行杂波谱仿真，结果如图4所示。

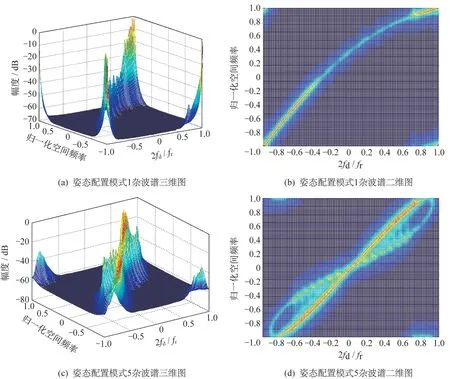
图4 不同姿态配置模式下的杂波谱图Fig.4 Clutter Spectrum under different attitude configuration modes

从杂波谱图可以看出，机载双基地雷达的空时二维杂波谱呈现出空时非线性的特点，且双基地配置模式对杂波谱的影响很大，不同双基配置模式时，杂波谱存在较大区别。与机载单基地雷达不同的是，由于双基地部署存在收发分置的原因，机载双基地雷达杂波可能会存在多个主瓣杂波。

4 结束语

相比机载单基地雷达而言，机载双基地协同探测雷达的杂波特性更复杂。本文首先分析了机载双基地协同探测雷达的杂波空时特性，然后在传统机载雷达杂波模型的基础上，考虑双基地分置时的接收波束和发射波束的相对关系等因素，提出了更精确的机载双基地协同探测雷达杂波模型。该模型考虑因素多，模型更精确。仿真结果表明，双基地配置模式对杂波谱的影响很大，并且由于双基地部署为收发分置，机载双基地雷达的杂波可能会存在多个主瓣杂波。在实际工作时，机载双基地雷达需要根据载机的几何位置和姿态进行实时分析和处理。