《几何论约》与近代数学几何术语

○ 李丽

(内蒙古师范大学 文学院，内蒙古 呼和浩特 010022)

明末清初是中外文化与学术交流的重要时期，近代数学知识的传播与术语的译介始于此。此间，最早译为中文的西方数学几何著作是《几何原本》，由利玛窦与徐光启合译并于1607年出版。然而，《几何原本》成书近百年，研读者甚少，究其原因，在于其内容之繁难，那么，如何将其删繁就简并使其数学几何知识得以普及，就成为当时我国数学家们的努力方向，杜知耕便是其中之一，而成书于1698年的《几何论约》正是其致力于此的重要成果。

一、《几何论约》的作者及成书背景

《几何论约》的作者是杜知耕，据《清史稿》记载，杜知耕字端甫，号伯瞿，柘城人(今河南柘城县)，康熙丁卯年举人，著有《几何论约》《数学钥》，收入《四库全书》。杜知耕的研究领域，除四书五经之外，还涉及天文、地理、律吕、历法、声韵、算学之类，其研究可谓博而精，李子金在《〈数学钥〉序》中以“凡读一书必求实，实有得；凡讲一事，实可得”评价杜知耕对学术的精审钻研。杜知耕曾以太学生身份游京师，在当时的国子监、钦天监学习过数学和历法，也曾留在国子监执教。此间，他第一次接触到利玛窦口述、徐光启笔译的《几何原本》并开始专于几何研究[1]206。

《几何约论》成书于1698年(清康熙三十七年)，正处于明末清初西学输入时期。近代西方数学的第一次传入是在明代万历年间，主要源于来华耶稣会的传教士。1581年(明万历九年)，耶稣会教士利玛窦来到中国，他是来华进行传教活动的第一个耶稣会传教士。利玛窦的到来正值明政府历法修改的迫切时期，传教士便趁此机会，从修改和编制历法入手，因此，近代西方数学知识传入的初期便是围绕历法修改进行的。此间，最早传入中国也是最早译为中文的西方数学著作是《几何原本》，由利玛窦与徐光启合译并于1607年出版。《几何原本》是一部古希腊杰出的数学著作，由古希腊数学家欧几里得编著而成，共十三卷。其中，第一卷至第六卷为平面几何学内容，第七卷至第十卷为数论内容，第十一卷至第十三卷为立体几何学内容。《几何原本》的译著引起了中国学者的关注，许多人开始致力于与之相关的编译工作，明代有孙元化的《几何用法》《几何体论》，清代有方中通的《几何约》(1661年)、李之铉的《几何易简录》(1679年)、梅文鼎的《几何通解》(1692年)，等等，杜知耕的《几何论约》(1700年)便是其中之一。

二、《几何论约》的命名与编纂体例

《几何论约》之所以命名为“论约”，如《四库全书》中的《几何论约》提要所言：“编取利玛窦与徐光启所译《几何原本》，复加删削，故名曰《论约》。”[2]1可见，《几何论约》是依据利玛窦与徐光启合译的《几何原本》加以删减而形成。关于删减理由，《几何论约》序中明确指出：“书成于万历丁未，至今九十余年，而习者尚寥寥无几，其故何与？盖以每题必先标大纲，继之以解，又继之以论，多者千言，少者亦不下百余言。一题必绘数图，一图必有数线。读者须凝精聚神，手志目顾，方明其义，精神少懈，一题未竟，已不知所言为何事。习者之寡，不尽由此，而未必不由此也。”[2]4可见，杜知耕认为《几何原本》成书时长，然而能够研读这部书的人却非常少，主要源于其内容繁难。

《几何约论》共七卷，其前六卷是在利玛窦、徐光启合译的欧几里得《几何原本》前六卷基础上，“就其原文，因其次第，论可约者约之，别有可发者，以己意附之，解已尽者节其论，题自明者并节其解，务简省文句，期合题意而止。又推义比类，复缀数条于末，以广其余意”[2]4-5，从而完成《几何约论》。由此可见，《几何论约》是依据《几何原本》的编写体例和顺序，尽量简省，另有可阐发之处，便附上自己的理解，已经解释全面的内容便简省其论述，题意明确的内容则省简其解说，追求文句简省以期契合题意即可。《几何论约》第七卷设置“增题”十五题和“后附”十题，用以扩充并阐发其余意。

《几何论约》删繁就简的目的在于“一题之蕴，数语辄尽，简而能明，约而能该，篇富既短，精神易括，一目了然，如指诸掌”[2]4，意在使编译内容简明概要，便于研读。以《几何原本》与《几何论约》卷一第六题为例进行对照：

解曰：甲乙丙三角形，其甲乙丙与甲丙乙两角等。题言甲乙与甲丙两腰亦等。

论曰：如云两腰线不等，而一长一短，试辩之。若甲乙为长线，即令比甲丙线，截去所长之度，为乙丁线，而乙丁与甲丙等本篇三次自丁至丙作直线，则本形成两三角形，其一为甲乙丙，其一为丁乙丙，而甲乙丙全形与丁乙丙分形同也，是全与其分等也公论九何者，彼言丁乙丙分形之乙丁，与甲乙丙全形之甲丙，两线既等，丁乙丙分形之乙丙，与甲乙丙全形之乙丙，又同线，而元设丁乙丙与甲丙乙两角等，则丁乙丙与甲乙丙两形亦等也本篇四是全与其分等也，故底线两端之两角等者，两腰必等也。

(《几何原本·卷一》)

(2)第六题：三角形，若底线两端之两角等，则两腰亦等。

(《几何论约·卷一》)

就卷一第六题而言，《几何论约》对《几何原本》做了大量删减，删减了图示、“解曰”及“论曰”的内容，只保留了命题内容。《几何论约》中，此类删减较多。杜知耕之所以就《几何原本》进行删减，意在使其内容简练而明确，概括而完备，篇幅短小而囊括精要，使研读者能够一目了然，易于读懂，进而增加研习者数量。

《几何论约》前六卷均有“卷首”部分，卷首的主要内容即“界说”“求作”和“公论”。“界说”主要就几何术语、概念进行解释，如杜知耕所言“凡造论，先当分别解说论中所用名目，故作界说”[2]5。“求作”主要是列出讨论的题目。“公论”即定理，其中，仅卷一之首包含“界说”“求作”“公论”三部分内容，即“界说三十六则”——点、线、面、角、形等几何术语的界定，“求作四则”——求作直线、求作圆等讨论题，如“一求：自此点至彼点，求作一直线”，即讨论两点间如何作一直线的问题。“公论十九则”——十九条几何定理，如“十论：直角俱相等”“十三论：两直线，止能于一点相遇”[2]7。《几何论约》其余各卷之首仅有“界说”。卷首之后是各卷具体内容，均为“题”，即题目或命题。第七卷是杜知耕增设的内容。(见表1)

表1 《几何论约》内容简表

具体而言，“题”即命题内容，其下大多涉及“解曰”“论曰”“法曰”“用法”“系”“增题”“耕曰”等内容，其中，命题本身不可或缺，其他部分则是辅助阐释和论述命题的内容。

(3)五题：两圆相交必不同心。

(《几何论约·卷三》)

(4)十题：一有界线，求两平分之。

(《几何论约·卷一》)

(5)十五题：凡两直线相交作四角，每两交角必等。

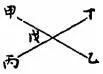
论曰：两直线相交，则甲戊丁、丁戊乙必等于两直角，甲戊丁、甲戊丙亦等于两直角本卷十三。是甲戊丁、丁戊乙两角并与甲戊丁、甲戊丙两角并等矣，试减同用之甲戊丁角所存丁戊乙、甲戊丙两角必等，余两角亦同此论。

一糸：推显两直线相交作四角与四直角等。

二糸：凡直线相交于一点，不论几许线、几许角，定与四直角等。

增题：一直线内出不同方两直线，而所作两交角等，即后出两线为一直线理同本题反言之。

(《几何论约·卷一》)

解曰：甲乙丙、丁戊己两角形，乙辛、戊庚两方形等高，其底乙丙、戊己，题言甲乙丙与丁戊己、乙辛与戊庚，皆若乙丙与戊己之比例。

增题：凡两角形、两方形等底，自相为比例，与其高之比例等。

耕曰：即前图以高为底，以底为高，其理自明。

(《几何论约·卷六》)

综上可见，《几何论约》卷三第五题仅有命题部分，卷一第十题包含命题和“法曰”“用法”，卷一第十五题包含命题和“解曰”“论曰”“系”“增题”，卷六第一题包含命题和“解曰”“增题”“耕曰”。其中，“解曰”意在解题。“法曰”是以作图法明确题意，“用法”可看作“法曰”的简省方式，是将作图法加以简省以求简明扼要。“论曰”就是结论，即定理。“耕曰”是杜知耕的理解和分析。“增题”是由“题”延伸扩展的题目。“系”即易于推导出的定律。

三、《几何论约》数学几何术语收录与释义

(一)《几何论约》数学几何术语收录

《几何论约》卷一至卷六“界说”部分收录并解释近代数学几何术语95个。其中，卷一收录点、线、角、面、圆、形等几何基本术语39个，卷二收录体现角线关系的几何术语3个，卷三收录体现圆与圆、线、角之间关系的几何术语23个，卷四收录体现圆与形之间关系的几何术语7个，卷五收录体现线、形比例关系的几何术语22个，卷六收录表示相似关系的几何术语2个(见表2)。《几何论约》界定的几何术语数量的62%，即59个术语沿袭至我国近代第一部西学术语词典《新尔雅》，可见其应用频率与传承性较强。

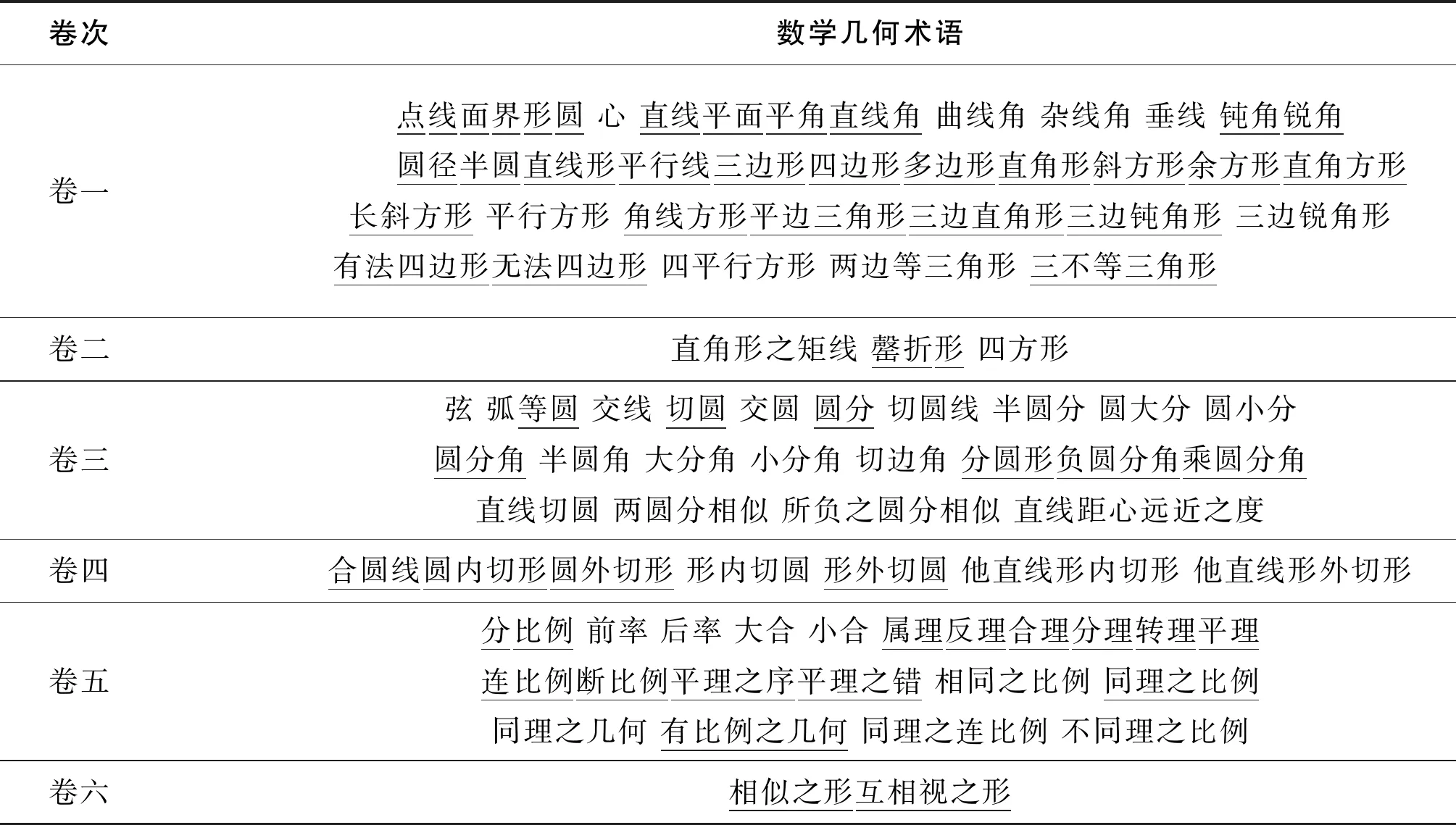
表2 《几何论约》“界说”数学几何术语收录表①

(二)《几何论约》数学几何术语释义方式

《几何论约》中近代数学几何术语释义方式较丰富，包括“义界”式、“义界+夹注”式、“义界+图示”式、“义界+夹注+图示”式。

1.“义界”式

“义界”式，由被释术语和释语组成。如：

(7)圆，自界至心任作几许直线俱等。

(《几何论约·卷一》)

(8)直角形，其角皆直，其边两两相等。

(《几何论约·卷一》)

被释术语“圆”“直角形”在前，释语为“自界至心任作几许直线俱等”“其角皆直，其边两两相等”，二者之间无形式标志。

(9)三边形，两边线等，为两边等三角形。

(《几何论约·卷一》)

(10)圆内直线形，以各角切圆界为圆内切形。

(《几何论约·卷四》)

被释术语“两边等三角形”“圆内切形”在后，释语为“三边形，两边线等”“圆内直线形，以各角切圆界”，二者之间以“为”作形式标志。

2.“义界+夹注”式

“义界+夹注”式，是在“义界”式基础上辅以夹注。“夹注”在《几何论约》中以小字形式呈现，目的在于补充或举例说明所释术语。例如：

(11)线，有长短，无广狭厚薄。线有曲有直。

(《几何论约·卷一》)

(12)形或在一界如平圆、立圆等形，或在多界之间如平方、立方及平立三角、六角、八角等形。

(《几何论约·卷一》)

被释术语“线”“形”在前，释语为“有长短，无广狭厚薄”“或在一界”“或在多界之间”，二者之间无形式标志。夹注“线有曲有直”“如平圆、立圆等形”“如平方、立方及平立三角、六角、八角等形”置于释语后用以补充或举例说明。

(13)三边形，三角皆锐角，为三边锐角形凡三边形恒以在下者为底，两旁者为腰。

(《几何论约·卷一》)

被释术语“三边锐角形”在后，释语为“三边形，三角皆锐角”，二者之间以“为”作形式标志。夹注“凡三边形恒以在下者为底，两旁者为腰”置于释语后用以补充说明。

3.“义界+图示”式

“义界+图示”式，是在“义界”式基础上辅以图示。其中，义界部分主要以“曰”“为”“谓”作形式标志，此类释义中往往伴有对应图示的举例说明。

(《几何论约·卷三》)

被释术语为“分圆形”，被释术语与释语之间以“曰”为形式标志。义界之后辅以图示说明。

(《几何论约·卷三》)

被释术语为“等圆”，被释术语与释语之间以“为”作形式标志，“如甲乙、戊己两径等，或丁丙、辛庚从心至圆界等，即两圆等”为举例说明，之后辅以图示。

(《几何论约·卷五》)

被释术语为“同理之比例”“连比例”“断比例”，被释术语与释语之间以“为”或“谓”作形式标志，“如甲与乙两几何之比例，偕丙与丁两几何之比例，其理相似为同理之比例”“如后图戊与己比、己又与庚比是也”“如前图甲自与乙比、丙自与丁比是也”为举例说明，其后辅以图示。

4.“义界+夹注+图示”式

“义界+夹注+图示”式，是在“义界”式基础上辅以夹注和图示。其中，义界部分主要以“为”或“曰”为形式标志。

(《几何论约·卷一》)

被释术语为“垂线”，夹注“角方，中矩曰直”针对释语“直”加以解释，义界之后辅以图示说明。

(《几何论约·卷一》)

被释术语为“平行线”，夹注“如甲乙丙两线”针对释语“两直线”加以举例，义界之后辅以图示说明。

(《几何论约·卷一》)

被释术语为“锐角”“钝角”，夹注“如前图甲乙丁角”“如甲乙丙角”分别针对被释术语“锐角”“钝角”用以举例，义界之后辅以图示说明。

综上，在明末清初西学东渐的时代背景之下，清初数学家杜知耕在利玛窦、徐光启合译《几何原本》基础上，删繁就简，取舍有度，编译而成《几何约论》。《几何约论》系统收录近代数学几何术语95个，包括点、线、角、面、圆、形等几何基本术语以及体现线、角、面、圆、形之间关系与体现线、形比例关系、相似关系的几何术语，运用义界辅以夹注、图示等多种释义方式加以界定，其界说图文并茂、精要概括，促进了近代数学几何知识及术语的普及与传承。

【 注 释 】

①表中标下划线的几何术语在《新尔雅》中有收录。