精细地形下的尾矿坝稳定性及溃坝模拟分析

孙鸿昌，郝 喆，杨青潮

（1.辽宁大学环境学院,辽宁 沈阳 110036；2.长安大学公路学院,陕西 西安 710064）

我国很多尾矿库已进入中老年期，接近或达到设计库容，尾矿坝也接近设计高度[1]；且多为上游式尾矿库，规模小、数量多，下游多分布人类生产生活区而形成“头顶库”[2]。受库水位影响，上游式尾矿库的浸润线不断变化，导致坝体饱和区范围改变，使得坝体强度受到严重影响，一旦发生溃坝，下游人民生命财产安全将受到严重损害[3-4]。因此，开展不同尾矿库水位下的尾矿坝渗流破坏及溃坝淹没范围的研究具有重要现实意义。

国内外学者在边坡稳定性及溃坝分析方面取得了一定的研究进展。刘克辉等[5]利用物理模型试验装置开展沟槽在不同弯曲度下的溃坝模拟研究，得出沟槽弯曲度与溃坝泥浆淹没深度呈非线性增加；郝喆等[6]结合Ansys 和FLAC3D软件，开展尾矿库加高增容过程中坝体渗流的稳定性分析及研究；陈胜亮等[7]利用多场耦合分析法，探讨了边坡非饱和渗流及其形变量等变化规律，得出边坡应变软化被非饱和渗流的时空分布所控制，易使饱和-非饱和分界带形成应力集中；皇甫凯龙等[8]应用二维溃坝数值模型分析计算溃坝水砂的流动状态，得出尾矿坝溃决水砂与水坝具有显著不同的流动状态；王兴华等[9]通过Fluent 数值模拟并考虑有水全溃坝、无水全溃坝、无水局部溃坝等3 种工况，研究分析尾矿库溃坝洪水的流动特性；Zandarín 等[10]采用流固耦合有限元方法模拟了溃坝诱因，指出毛细水是影响渗透性较差坝体稳定的关键因素；Yuan 等[11]利用Fluent 软件从水砂流速、冲击力和淹没深度等方面分析了尾砂流的演进特征，得出了下游各位置的水砂分布；孔祥云等[12]通过自制溃坝试验装置研究分析尾矿库水位变动工况下的坝体位移形变情况；姚志坚等[13]利用“等效糙率”方法代替下游构筑物，并将该方法应用于二维溃坝模拟中；李强等[14]针对实际尾矿库，将流固耦合与强度折减相结合，开展尾矿坝滑带形成过程及滑带空间分布研究；侯圣山等[15]采用FLO-2D 模型计算了降雨条件下泥石流的流动状态及运动特征，并划分了泥石流灾害危险性分区图。

以上针对尾矿坝稳定性与溃坝的模拟分析多是独立进行的，多采用实际地形概化后的二维模型，缺乏三维尾矿坝稳定性与精细地形下溃坝过程的综合分析，也缺乏下游构筑物对水流滞水作用的可靠处理方法。本文以辽宁省某上游式尾矿库为例，开展正常水位、洪水位、漫顶水位等3 种工况下尾矿坝稳定性研究，采用等效糙率方法将下游构筑物与地形对溃坝泥砂的阻水作用进行替代模拟，同时实现尾矿坝稳定性分析与高精度地形下尾矿库水砂两相流三维溃坝模拟相结合，开展尾矿坝稳定性-溃坝的综合剖析及水砂在下游地形流动特点分析，为尾矿库安全运行、灾害分析和应对策略提供科学依据。

1 计算原理

1.1 非饱和流固耦合分析

尾矿坝内由于浸润线的存在，使得浸润线以下形成饱和区，以上形成非饱和区，而库内水位高度变化引起的浸润线变化也可认为是饱和-非饱和渗流过程[16]。FLAC3D中非饱和流固耦合微分方程由平衡方程、连续方程、基质吸力方程组成[17]，平衡方程为：

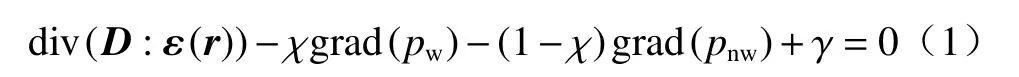
式中：D——刚度张量；

ε(r)——应变张量；

r——位移向量；

χ——非饱和土参数；

pw——孔隙水压力/Pa；

pnw——孔隙气压力/Pa；

γ——土体重度/（N·m-3）。

将达西定律与质量守恒方程联立得连续性方程：

式中：ρw——水密度/（kg·m-3）；

kw、knw——水、气渗透系数/（m·s-1）；

γw、γnw——水、气重度/（N·m-3）；

Z——位置水头/m；

Sr——饱和度/%；

n——孔隙率；

H——Henry 系数。

非饱和尾矿土的基质吸力与土体含水率有关，土-水特征曲线方程为：

式中：Sr0——初始饱和度/%；

n0——初始孔隙率。

通过尾矿库流固耦合求解，计算出其应力场及孔压场的分布，加入摩尔-库伦模型，结合强度折减法，实现渗流与强度折减同步进行，从而计算尾矿坝稳定性。

1.2 溃坝泥砂分析

1.2.1 VOF 模型

尾矿库溃坝可看作溃决水砂与大气多相流动，初始阶段及溃坝阶段水砂均与大气存在接触，而VOF 模型在多相流体模拟分析中效果最佳[18]。VOF法在计算域内对模型中的每一相引入一个变量F，其为在网格内各相流体的体积与流体空间总体积的比值，水气界面的追踪可通过求解F的输运方程[19]：

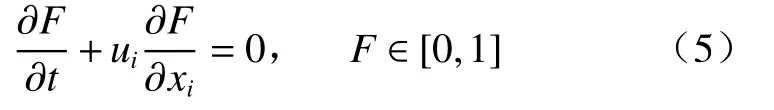
式中：F=F(x,t)——空间和时间函数；

x——坐标向量，其分量为xi；

ui——速度分量。

1.2.2k-ε湍流模型

尾矿库溃坝水砂往往以湍流的形式向下游快速无规则流动，而Fluent 提供了多种湍流模型 。本次计算参考刘学炎[20]的溃坝模拟研究成果，选取应用广泛且适用于多相流模拟的标准k-ε湍流模型。

k-ε模型是基于能量方程和扩散速率方程得出的一种经验模型，其湍流动能k和耗散率ε控制方程[21]分别为：

k方程：

ε方程：

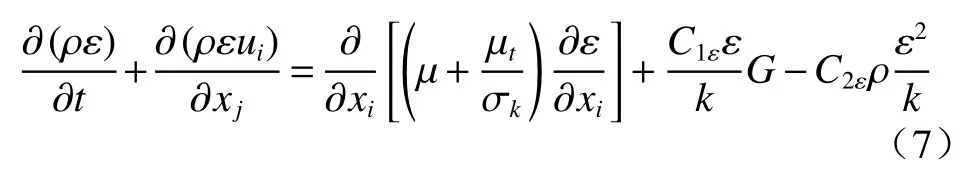
式中：G——紊动能生成率/（m·s-1）；

ρ——流体密度/（kg·m-3）；

µ——分子动力黏性系数；

μt——紊动黏性系数；

k——紊动动能/（m2·s-2）；

ε——紊动耗散率/（m2·s-2）；

σk——k的紊流普朗特数；

C1ε、C2ε——经验常数。

1.2.3 黏滞系数

溃坝水砂黏滞系数的影响因素众多，本文采用水砂浓度得出的黏滞系数计算方程[22]：

式中：η——水砂动力黏度/（Pa·s）；

µ0——水的黏滞系数，常温下 µ0为0.99；

Cv——水砂浓度/%。

经勘察得水砂浓度为67%，则η为15.84 Pa·s。

1.2.4 最大泄砂流量

洪水漫顶造成尾矿库从开始溃坝到稳定的时间短暂，可按瞬溃处理[23]。瞬时垂向局部溃坝时，存在高度h1的残坝，坝址最大泄砂流量[24]为：

式中：QM——坝址泄砂流量/（m3·s-1）；

B——溃坝前水面宽度/m；

H0——溃坝前水深/m；

g——重力加速度/（m·s-2）；

h1——残坝高/m。

1.2.5 下游溃坝水砂流量

溃坝水砂在不同位置处的流量受距离和地形影响显著[25]，而本次溃坝模拟既有山谷狭窄地形，又有农田平缓地形，因此对下游重要构筑物位置的流量分析尤为重要。下游水砂流量计算方程[26]：

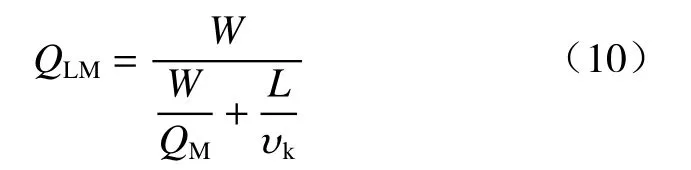
式中：QLM——下游L处最大流量/（m3·s-1）；

W——库容/m3；

L——距坝址距离/m；

υk——经验系数，山区河道取7.15，平原河道取3.13。

2 工程概况及相关参数

2.1 模拟区域概况

某上游式尾矿库位于辽宁省，尾矿库及下游地形见图1。坝体由初期坝及后期堆积坝组成，加高增容后总坝高约102 m，坝顶长203 m，总库容约16.95×106m3，坝体平均外坡比为1∶4。模拟区域东西方向长1.8 km，南北方向平均宽650 m。该尾矿库下游为办公区、选矿场、矿料堆积场、农田、温室以及砖厂。根据《尾矿堆积坝岩土工程技术规范》（GB 50547—2010）[27]，此尾矿库等级标准为二等库，尾矿坝级别为2 级。

图1 尾矿库及下游地形Fig.1 Topography of the tailings pond and the area downstream

2.2 尾矿坝物理力学参数

将现场采的原状尾矿土试样进行直剪速率为0.02 mm/min 的慢剪试验，得到黏聚力及内摩擦角。经筛分的样品烘干后，以含水率为5%的梯度制备尾细砂、尾粉砂、尾粉质黏土样品至饱和，其饱和含水率分别为35%、33%、30%。通过接触滤纸法对样品进行基质吸力测定，经VG 模型[28]拟合得到土-水特征曲线（图2）。结合尾矿库现场勘察结果，得到尾矿坝基本物理参数（表1）。

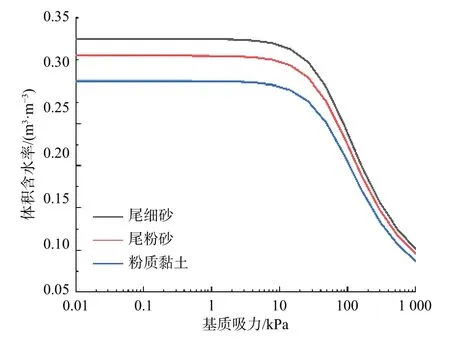
图2 尾矿坝各土层土壤土-水特征曲线Fig.2 Soil water characteristic curve of each layer of the tailings dam

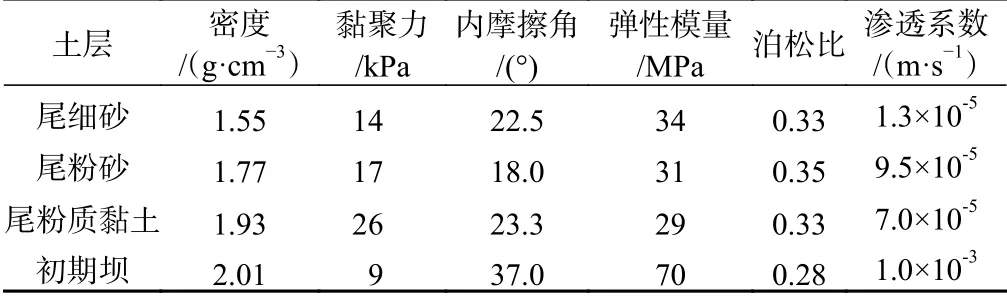
表1 尾矿坝物理力学参数Table 1 Physical and mechanical parameters of the tailings dam

3 库水位变化对稳定性的影响

根据前期矿山地质钻探资料，结合本次现场调查结果，建立尾矿库稳定性计算模型（图3）。尾矿库稳定性模拟计算通过FLAC3D软件实现，通过赋值孔隙水压力将坡表及初期坝的边界条件设为透水边界，在进行渗流计算时通过摩尔-库伦本构模型对赋予物理力学参数的土体进行强度折减。为了更好地对数值模拟结果进行定量分析，对模型设置A、B、C、D 等4 个关键点（图3）进行位移形变监测。

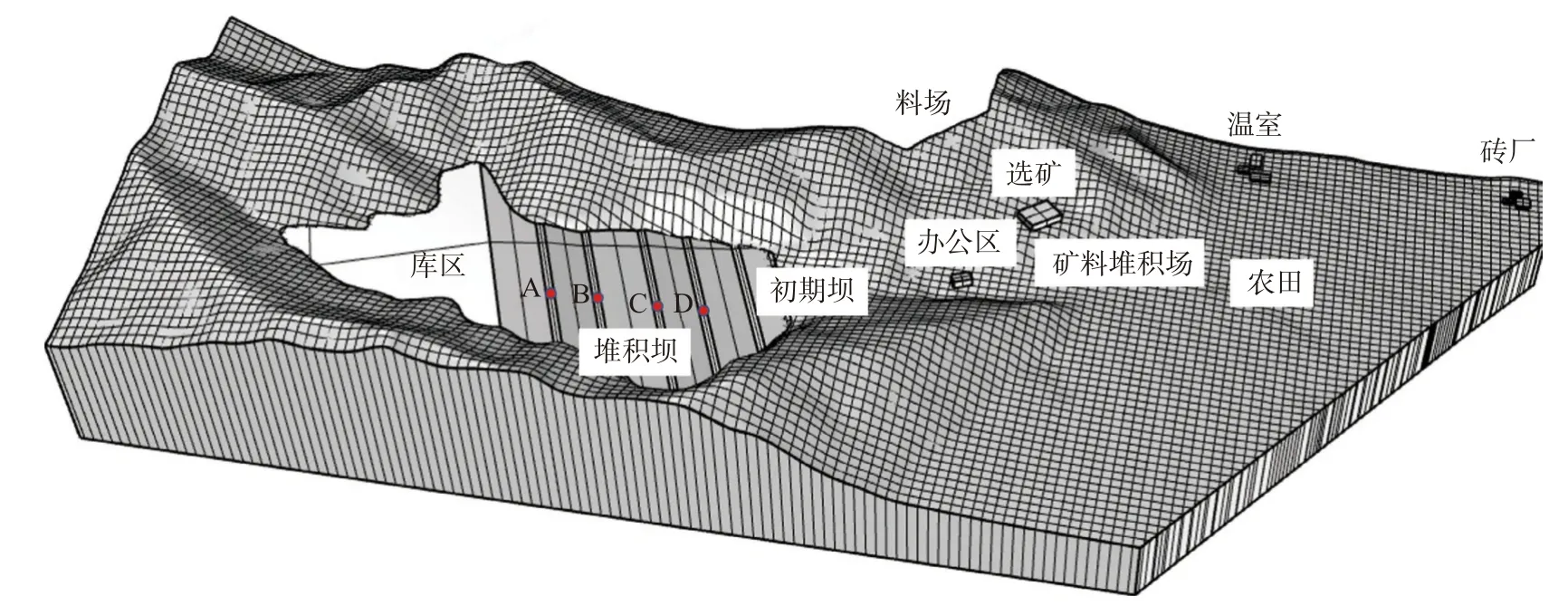
图3 尾矿库模型及监测点位置Fig.3 Tailings pond model and location of detection points

3.1 库水位变化对渗流的影响

根据《尾矿设施设计规范》（GB 50863—2013）[29]中的上游式尾矿库最小安全超高（洪水位与坝顶之间高差）和干滩长度（坝顶与库内水边线的水平距离）限值（表2），可知研究区尾矿库洪水位的安全超高和干滩长度分别为1.0 m 和100 m。结合实际尾矿库的现场勘察结果，得到尾矿库正常水位运行情况下的安全超高为1.3 m、干滩长度122 m。基于此，将库内水位高度划分为漫顶水位（安全超高0 m）、洪水位（安全超高1 m）及正常水位（安全超高1.3 m）。通过计算得出各水位下的浸润线形态（图4）。

表2 上游式尾矿坝的最小安全超高和最小干滩长度Table 2 Minimum safe superelevation and minimum dry beach length of the upstream tailings dam

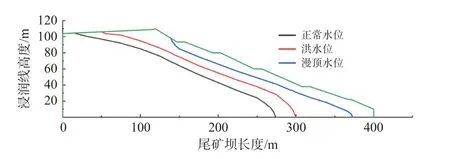
图4 不同水位浸润线位置Fig.4 Location of phreatic line at different water levels

由图4 可知，浸润线的埋深随尾矿库水位的升高而变小，由正常水位提升至洪水位，浸润线埋深下降5～8 m，干滩长度缩短24 m；由洪水位升高至坝顶，浸润线埋深下降5～6 m，干滩长度缩短为0 m。而漫顶水位工况下，浸润线埋深较小，坝顶处稳态饱和区沿坡面向下运移8 m 左右，逐步到达1 级台阶处，坝顶部分达到饱和状态，土体的黏聚力迅速下降，极易造成坝体局部失稳从而发生溃坝事故。

3.2 库水位变化对剪切带及稳定性系数的影响

通过渗流场与应力场耦合，利用强度折减法来分析现场正常水位、洪水位、漫顶水位等3 种工况下坝体的稳定性。为便于结果分析，截取尾矿坝中线位置处的稳定性计算结果剖面，图5 为3 种水位工况的剪切带。

图5 不同水位剪切带Fig.5 Shear zones with different water levels

由图5 可知，库水位对剪切带及尾矿坝稳定性有显著影响。剪切应变率是剪切带随坝体变形破坏的速率，随水位上涨，坝体剪切应变率增大1 个数量级，表明水位变化的影响使剪切应变加快。正常水位时，剪切应变率最大值为2.95×10-6，出现在3 级台阶处。从正常水位升高到洪水位时，剪切应变率增大为5.78×10-5，尾矿坝稳定系数由1.80 下降至1.32。剪切带在纵向上不断向坝体内部延伸，剪切带从最初10～12 m 深发展到15～18 m 深；在横向上从坝顶贯穿到3 级台阶发展到从坝顶贯穿到4 级台阶，水平上增加了20 m。而水位达到坝顶时，剪切应变率进一步增大为3.32×10-4，出现在1 级台阶处，尾矿坝稳定系数由1.32 下降到1.18。剪切带急剧缩短，只在1 级台阶处贯穿。究其原因，洪水漫顶时，浸润线沿坡面向下运移使得坝顶处尾矿土含水率远大于其他位置土壤，达到局部饱和。

3.3 库水位变化对坝体变形的影响

由于水位变化使得坝体内部应力发生改变，导致坝体受应力变化发生形变，形变进一步影响尾矿坝土体结构，使其稳定性明显下降。因此在计算完成后提取监测点A、B、C、D 的位移变化曲线图（图6），对3 种工况下坝体变形作出定量化分析。

由图6 可知，各水位工况下尾矿坝形变量差异显著，总体呈先急增后平稳趋势。计算初期，各监测点位移数值迅速增加，在设置大变形情况下坝体水平变化明显，在2 000～4 000 步之间，位移曲线产生拐点；在计算中期时，坝体形变量在0.02～0.05 m 之间上下小幅度波动，此阶段坝体未产生较大形变；进入计算后期，计算不断收敛，位移曲线不再发生变化。

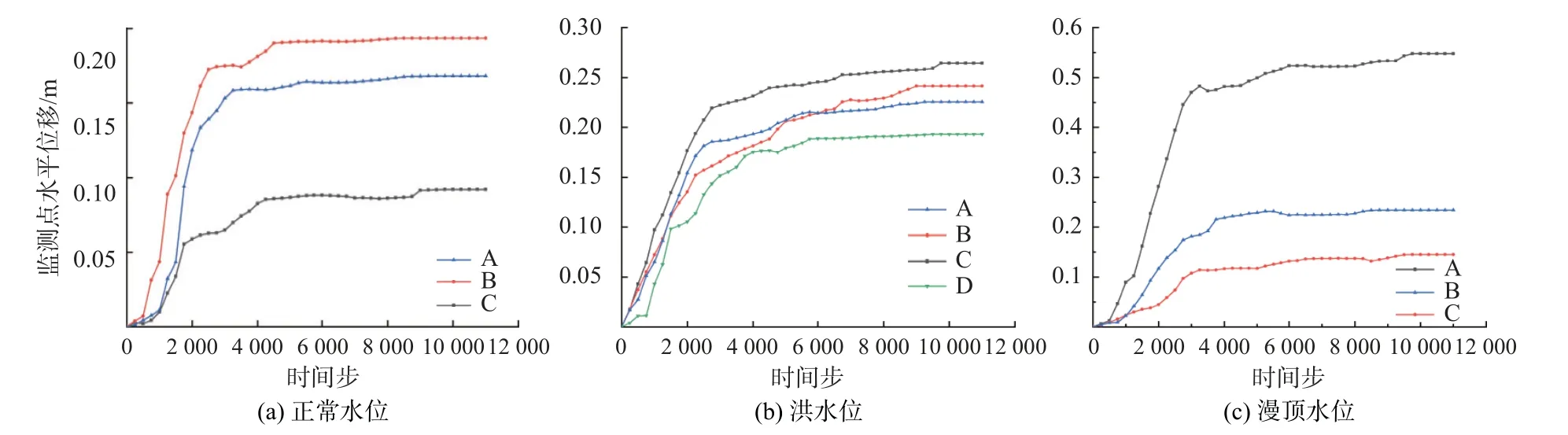
图6 各监测点位移变化曲线图Fig.6 Displacement change curve of each monitoring point

正常水位时，监测点A、B、C 监测到坝体形变量，变化量值为B＞A＞C，分别为0.19，0.17，0.09 m。洪水位时，监测点A、B、C、D 监测到坝体形变量，变化量值为C＞B＞A＞D，分别为0.26，0.24，0.22，0.19 m。漫顶水位时，监测点A、B、C 监测到坝体形变量，其变化量值为A＞B＞C，分别为0.54，0.23，0.15 m。综上，尾矿坝位移形变最大值位置应处于潜在滑面中线与坡面交点偏下处，与剪切应变率最大位置略有差异。究其原因，剪切应变率最大位置处表示坝体失稳时优先破坏的位置，而临空面处于破坏处之上，在向下滑动过程中位移变化较大。

4 溃坝模拟

上述稳定性分析结果表明，漫顶水位时坝顶产生局部饱和，溃坝风险最大，以此工况作为尾矿库溃坝模拟的基础。漫顶水位时尾矿坝潜在滑带由坝顶贯穿到1 级台阶，此时稳定系数最低，仅为1.18。规范未提供漫顶稳定系数，洪水漫顶出现的概率完全高于地震荷载特殊工况。由于稳定系数1.18 略高于特殊工况稳定系数1.15，因此可以认为尾矿坝处于欠稳定状态。根据图5，将坝顶到1 级台阶的高度作为尾矿库溃坝模拟溃口的高度，其值为13.2 m。将FLAC3D的计算结果调入到Ansys-Fluent 中，进行尾矿库溃坝水砂在下游流动状态的模拟计算。

4.1 模型建立及边界条件

采用Rhino 和Fluent 软件进行建模及分析计算。在Rhino 中通过尾矿库的等高线建立复杂溃坝模拟地形图。将建立好的模型导入Fluent 软件中进行计算，使溃坝数值模拟结果与实际情况更相符。在Fluent 中设置模型边界条件，将模型上部空气界面设置为压力入口，四周界面为压力出口，山体地形和坝体为墙体[30]。水砂受地形摩擦力影响，而不同地形对水砂的摩擦影响不同，本文通过等效糙率法来控制地形对水砂的摩擦影响[31]，糙率值的取值见表3。

表3 地形对水砂摩擦影响的糙率值Table 3 Influence of topography on the water sand friction roughness value

4.2 模拟结果与分析

4.2.1 溃坝水砂淹没范围

根据Fluent 计算结果，得出尾矿库发生溃坝后溃决水砂在不同时刻流动演进情况的体积分数（Volume fraction）云图（图7）。由图7 可知，t为0 s 时，尾矿库内水砂和堆积坝处于相对静止状态，随着时间推移，堆积坝坝顶出现溃口瞬间溃决。0～100 s 时，溃口附近尾砂由于水流拖曳力作用冲刷形成初期水砂混合流，后方尾砂随之开始滑动；100 ～300 s 时，尾矿库内水砂在重力势能的作用下快速流出；300～700 s 为水砂流在山谷内的汇流演进阶段，300 ～500 s 时溃坝水砂淹没下游办公区，溃坝水砂的前端来到矿料堆积区，水砂速度在高差明显的山谷内将会进一步变大；700 s 以后，溃坝水砂在农田等地势平坦处向四周发散流动，700～900 s 时，前端水砂流到低势能区，水砂淹没范围更加广泛，但水砂伴随尾砂料之间的碰撞摩擦其速度将会降低；1 300 s 之后，水砂趋于停止。

图7 不同时刻溃坝水砂流演进云图Fig.7 Cloud chart of water and sand flow evolution of dam break at different times

4.2.2 溃坝水砂速度演进

溃坝水砂在山谷及农田两处的流动状态分别为汇聚流动和发散流动，山谷及农田的水砂速度云图见图8。由图8 可知，500 s 时，山谷内地势陡峭，云图颜色由堆积坝上的蓝色转为山谷内的黄绿色，水砂流速进一步增大。900 s 时，农田处地势平缓，云图颜色由山谷内的深红色转为黄绿色，水砂发散流动，流速降低。溃坝水砂流速整体状态呈“增大—增大—减小”趋势，主要表现为在堆积坝受重力作用从0 逐渐增大，流经山谷受地形地势影响流速进一步增大，到达农田时水砂发散流动，流速开始降低，山谷内办公区附近流速最大。

图8 溃坝水砂速率云图Fig.8 Cloud chart of water and sand velocity of dam break

4.2.3 下游水砂流量

此上游式尾矿库溃坝水砂最终淹没范围东西方向长1 362 m，南北方向平均宽440 m，淹没面积约为0.6 km2。初期坝东方向的办公区、矿料堆积场及下游农田处于主要淹没区内，而选矿厂房和料场地势较高，基本不受溃坝影响。由式（9）（10）计算可知，此尾矿库最大泄砂流量为2 905.43 m3/s，下游470 m 处办公区出现最大水砂流量为2 872.64 m3/s，下游1 020 m 处农田出现最大水砂流量为2 651.62 m3/s。办公区与农田相距550 m，最大水砂量相差221.02 m3/s，由式（10）可知，随着L的增大，QLM逐渐减小。因此，在尾矿库选址时，距下游重要建筑物距离应作为优先考虑因素。

5 结论

（1）尾矿坝浸润线埋深随库水位升高而不断变小，漫顶水位时，坝顶浸润线沿坡面向下运移，使得坝顶部分达到局部饱和，土体黏聚力急剧下滑，造成优先滑动破坏现象。

（2）从正常水位到洪水位时，剪切带在纵向上不断向坝体内部延伸；在横向上从坝顶贯穿到3 级台阶发展到从坝顶贯穿到4 级台阶，洪水漫顶时，浸润线沿坡面向下运移使得坝顶局部达到饱和、优先发生破坏，剪切带急剧缩短。

（3）由FLAC3D稳定性分析软件计算出失稳时的潜在滑面，以此作为溃口，利用Rhino 建立尾矿库下游精细地形，将稳定性分析结果作为Fluent 中溃坝模拟初始条件并进行计算，得出水砂的流动状态：在山谷狭窄地形下，水砂具有流速快，水砂流量大，淹没范围小的汇集流动；在农田等平坦地区，水砂具有流速慢，水砂流量小，淹没范围广的发散流动。

（4）通过设置地表糙率，能够有效降低模拟结果与实际情况的偏差；发生溃坝后，溃口水砂在重力势能和堆积坝体的摩擦共同作用下迅速向下游流动，由于山谷内高差影响，此时水砂流速最大；随后，溃口的水位不断降低，受下游地势平缓和地表面的粗糙程度影响，水砂不会向下游产生较大区域的流动。