动态载荷下大理岩断口形貌特征试验研究

2022-05-23王伟祥王志亮贾帅龙卢志堂

水文地质工程地质 2022年3期

王伟祥，王志亮，贾帅龙，卢志堂

（1.合肥工业大学土木与水利工程学院,安徽合肥 230009；2.合肥工业大学资源与环境工程学院,安徽合肥 230009）

随着社会经济的不断发展，越来越多的大型工程逐渐向地球深部发展，如核废料深埋处置、深部矿产资源开采及水电站地下厂房修建等。这些深部工程均不可避免地涉及到岩石的力学性质，而岩石细观结构与力学性质有着必然的联系。由于能直观记录岩石破坏过程中微裂纹从萌生到断裂的全过程，岩石断口形貌学为相关研究开辟了新的思路[1-2]。

迄今，许多学者对岩石断口形貌进行了研究。李先炜等[2]对岩石多种受力形式的断口进行电镜扫描试验，总结了岩石拉断断口和剪断断口花样特征。梁昌玉等[3]通过单轴压缩试验分析了花岗岩在静态和准动态加载下断口形貌及细微观破裂模式的差异。闻名等[4]采用大直径分离式霍普金森压杆（SHPB）对不同温度等级下砂岩进行动态压缩试，发现岩石断裂程度随着应变率的提高而增加。赵康等[5]对岩爆断口进行了探究，得出劈裂岩块断口多呈台阶状花样，属张拉或剪切型断裂。针对断口形貌的率相关性，Zhang 等[6]利用SHPB 对岩样进行楔形加载，指出辉长岩试件断口附近的分岔裂纹随着加载速率的增加而增加。李晓锋等[7]发现随应变率的增加，岩石的破坏形态将由完整型到劈裂破坏再到粉碎破坏转变，且在较低应变率下，岩石破碎程度与应变率存在正相关性。谢和平等[8]将分形理论引入到岩石力学中，为定量研究岩石损伤破碎程度提供了全新的手段。随后，研究人员[9-10]对此开展深入研究，发展和完善了分形理论-岩石力学的框架体系，结果表明岩石细观裂纹具有统计自相似性，用分形理论去定量分析断口粗糙程度是具有可行性的。

综上可知，国内外学者已对岩石断口形貌特征及其演化规律开展了大量研究，但其大多只考虑了静态受载后的断口情况，对于动载荷载下同时探析压缩和劈裂作用的影响机制鲜有报道。众所周知，在实际工程施工中（如爆破开挖、机械掘进等），岩石受力情况非常复杂，可能会发生动态拉压等复杂作用。因此，本文拟采用钨灯丝扫描电镜对锦屏大理岩冲击压缩和动态劈裂后试样断口进行细观观察，并结合分形几何理论，对岩样断口细观形貌进行定性与定量分析，力求得到具有参考价值的结论。

1 大理岩动态压缩与动态劈裂试验

1.1 试样制备

本试验中大理岩取自四川锦屏二级水电站深埋引水隧洞，所有试样均从同一块完整的大理岩块上取得。大理岩的主要成分有白云石(69.31%)、方解石(20.35%)、石英(5.44%)和少量其它矿物。

为了满足应力均匀性要求，岩样尺寸选为Φ50 mm×25 mm，即高径比取为0.5[11]。试样两端面经仔细打磨，确保其不平行度小于0.05 mm，以降低由于受到偏心受压导致的应力集中带来的误差影响。该岩样基本物理力学参数列于表1 中。

表1 大理岩基本物理力学参数Table 1 Physical and mechanical parameters of marble

1.2 试验原理及方案

本次试验在分离式SHPB 上完成，如图1所示。该系统主要由高压气腔室、子弹、入射杆、透射杆、缓冲装置、数据采集及分析系统构成。其中，子弹长为400 mm，入射杆和透射杆的杆长分别为2 400 mm 与1 400 mm。子弹和所有杆件均采用高强度合金钢制成，密度为7 900 kg/m3，弹性模量为210 GPa。为了改善入射波形以减小试验误差，在入射杆前端面中心处粘贴一直径10 mm、厚度1 mm 的橡胶片作为波形整形器（图1）[12]。

图1 SHPB 装置Fig.1 SHPB device

当子弹以一定速度撞击入射杆时，在入射杆中产生入射波，试样在应力波的作用下产生变形，导致一部分应力波反射回入射杆形成反射波，另一部分应力波穿过试样在透射杆中形成透射波。应力-应变关系可通过“三波法”得出[13]：

式中：Ae——输入杆或输出杆截面积；

As——试样截面积；

Ls——试样长度；

Ce——纵波波速；

Ee——钢杆弹性模量；

εI(t)、εR(t)、εT(t)——入射波、反射波与透射波的应变信号。

为确定合理的冲击弹速值，预先对试样进行“试冲”，以试样有明显破碎时弹速为冲击弹速最低临界值，由此确定出动态压缩试验冲击弹速V0分别为9.0，13.0，16.5 m/s；动态劈裂试验V0分别为5.0，6.5，9.0 m/s。

1.3 试验结果及分析

图2 为动态压缩和动态劈裂试验下的原始波形图，入射波均为经整形后波形，上升沿趋势较缓且入射波形无明显振荡。易见入射波、反射波及透射波峰值均随冲击弹速增加而增大。此外，由式（2）（3）可知，试样的平均应变率及动态强度均随着弹速的提高而增大。

图2 原始波形图Fig.2 Diagram of the original waveform

图3 为动态压缩和动态劈裂下试样的动态应力曲线，其中符号In、Re、Tr 分别表示入射波、反射波及透射波。易见，入射波与反射波之和与透射波曲线在峰值前基本重合，表明在动态压缩和动态劈裂下，试样在加载过程中均能满足应力均匀性假设。经“三波法”计算，冲击试验3 个弹速下峰值应力分别为142.6，162.5，187.8 MPa；劈裂试验3 个弹速下峰值应力为别为12.3，14.0，18.9 MPa。

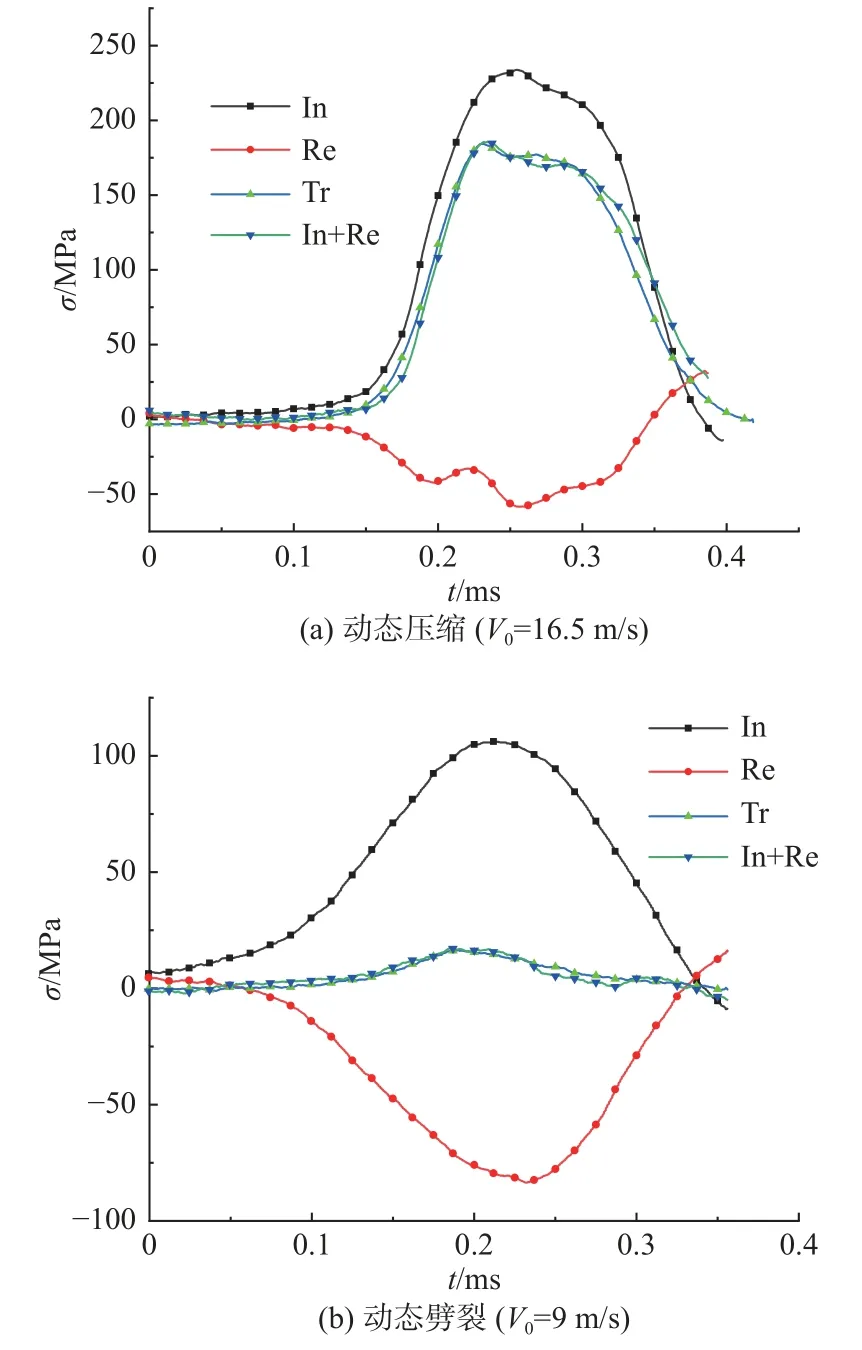
图3 动态应力均衡图Fig.3 Diagram of dynamic stress balance

2 断口形貌特征研究

2.1 试样制备和试验设备

在大理岩岩样断口处取10 mm×10 mm×4 mm 的扁平长方体切片，非断口面打磨平整。为了得到清晰准确的图像，使用丙酮清洗试样，待其自然晾干。接着，将样品台座放入喷金仪中，抽真空后对断口进行喷金处理以增强岩石导电性。最后，借助于JSM-6490LV 型钨灯丝扫描电镜对大理岩动载下断口形貌进行观察。

2.2 动态劈裂下大理岩断口形貌

图4 为不同弹速下大理岩断口形貌。由图4（a）可看出，在弹速为5.0 m/s 时，断口花样较大，主要是以沿晶破坏（大量冰糖状花样）为主，少量为沿晶-穿晶耦合断裂。一般来说，岩石两晶粒交界即晶界的位置相对于晶粒本身更加脆弱，在低弹速下易在此发生断裂，且断口一般相对光滑、清洁，棱角清晰呈多面体状[1]。

由图4（b）可见，在弹速为6.5 m/s 时，岩样断口表面较为平整，微裂隙持续发育，断口表面粗糙程度略有上升。此外，还出现代表穿晶断裂的解理台阶状断口。解理台阶通常有2 种形式[1]：处于不同高度但是相互平行的2 个解理面，可能通过次生解理形成解理台阶，通常此断面相对光滑；在高能量快速释放下，连接面受拉或受剪破坏，断口一般相对粗糙。

穿晶破坏形式的特点是裂纹撕裂晶界并穿越晶体内部，是高弹速情况下岩石常见的断裂形式[1]。由图4（c）可见，在弹速为9.0 m/s 时，大理岩断口整体粗糙度进一步提高，表面出现大量岩粉，细部花样小而密。此时，断口以穿晶断裂模式为主，伴随少量的沿晶断口。

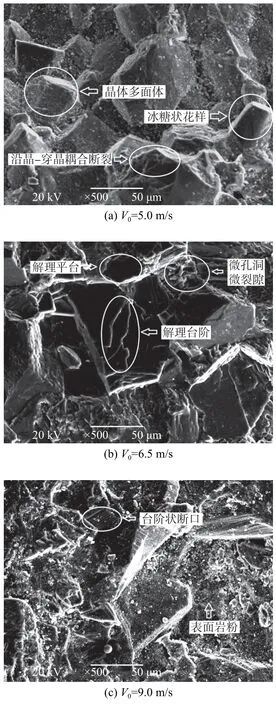
图4 不同弹速下大理岩动态劈裂断口形貌Fig.4 Dynamic splitting fracture morphology of the marble under different impact velocities

2.3 动态压缩下大理岩断口形貌

图5 为不同弹速下冲击压缩断口形貌。由图5（a）可见，当弹速为9.0 m/s 时，岩样断口表面无明显岩粉，断口整体花样较大，局部平坦，且微裂隙、微孔洞少量发育。这种工况下，断口形貌以沿晶-穿晶耦合断裂模式为主，局部可呈现出沿晶断裂形式。

由图5（b）可见，当弹速为13.0 m/s 时，岩样断口细部粗糙度略有提高，微裂隙持续发育，出现蜿蜒曲折的非主断面上的二次裂隙。同时，观察到大量密集的解理断口（如河流状花样、平行条纹花样及台阶断口等）。此外，沿晶断裂形式显著减少且出现准解理断口。实际上，准解理断裂是介于脆性断裂与延性断裂之间的一种断裂方式，表面既有较大塑性变形产生的撕裂棱，又存在河流状花样[14]。在动载下断裂耗能情况由低到高分别是：胶结物质断裂→沿晶断裂→穿晶断裂→准解理断裂→韧性断裂[15]。所以，随着冲击弹速的增大，入射能量逐渐增加，导致试样以耗能更大的断裂形式破坏。

由图5（c）可见，当弹速为16.5 m/s 时，大理岩断口细部花样小而密，粗糙程度明显提高且伴随有较多的岩粉，观察发现断口花样以穿晶断裂形式为主，且代表剪切破坏的滑移分离断口。

图5 不同弹速下大理岩冲击压缩断口形貌Fig.5 Dynamic compression fracture morphology of the marble under different impact velocities

2.4 断裂表面粗糙程度分形特征

由于岩石的非均质性，其断口表面粗糙程度很难采用传统的方法进行描述。因此，不少学者采用分形几何学理论对岩石的断裂面细观特征等进行研究[8-10]。目前，关于估算断裂面真实分形维数的计算方法有很多，考虑到盒维数法计算过程相对简单且理论成熟。因此，此处拟采用分形理论中的盒维数法来计算不同弹速下岩样破坏断口的分形特征，其具体思路为[16]：先用均匀分割的网格图像去覆盖分形；接着，数出覆盖这个分形需要多少边长为的小格子；最后，利用极限的思想精化网格（即→0）时，计算出该图形分形维数。

若所研究对象具有自相似性，则N(ε)—ε关系可由下式表达[16]：

式中：a——常数。

对式（4）两边取对数得：

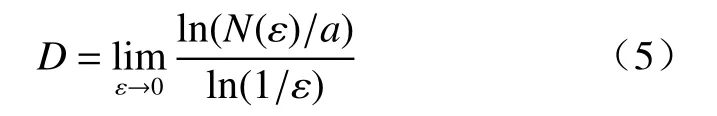
式中：D——计算所得的分形维数；

ɛ——几何形体的尺寸；

N——覆盖图形所需的最小的半径不超过的几何形体的个数。

根据计算结果绘制 lnε-lnN曲线，通过最小二乘法得出拟合线性方程，其斜率大小就是计算的分形维数值。

由于计算机无法直接识别SEM 试验得到的照片，故先要将所得的图片信息转化为计算机可以识别的数字信息。通过MATLAB 编程，将图片实现二值化（图6），转化为计算机可以识别的0 和1 矩阵，进行分形维数的计算。FarctalFox 是一款专门用于计算图像分形维数的软件，其工作原理本质上与盒维数法相同[17]，计算公式为：

图7 是根据图6 得出的大理岩试样断口分形维数回归线（可决系数R2为0.99），表明断口细观形貌具有统计自相似性，可通过这种分形方法大理岩断口形貌粗糙程度进行定量分析。

图6 处理前后图像对比Fig.6 Comparison of the pre-and post-treatment images

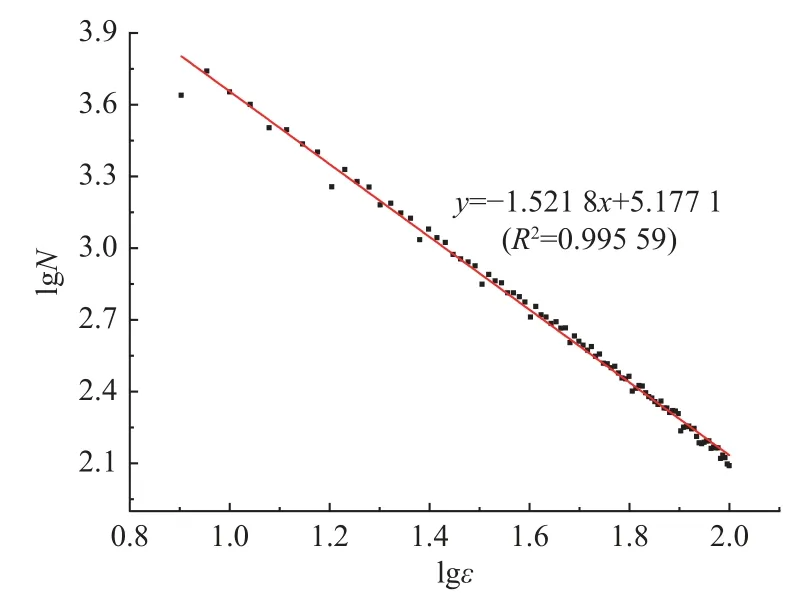
图7 分形维数处理结果Fig.7 Fractal dimension processing results

分形维数的变化能有效地反映出岩石断口断裂模式发展的趋势。图8 反映的是分形维数与放大倍数之间的关系，由于电镜可观察视野随着放大倍数的增大而减小，可观察的晶粒结构愈加清晰简单，这导致分形维数值随着放大倍数的增大而减小。同时，可见放大倍数对分形维数值具有较大的影响。因此，为了更好地对比分析冲击弹速对断口分形维数的影响，必须采用统一的标准。由图8 可以看出，500 倍时既可较好地表现出岩样断口形貌，又不会过度影响裂隙和晶面结构的复杂程度，故本文选取每组样本放大500 倍下的平均分形维数为其断口细观结构分形维数。

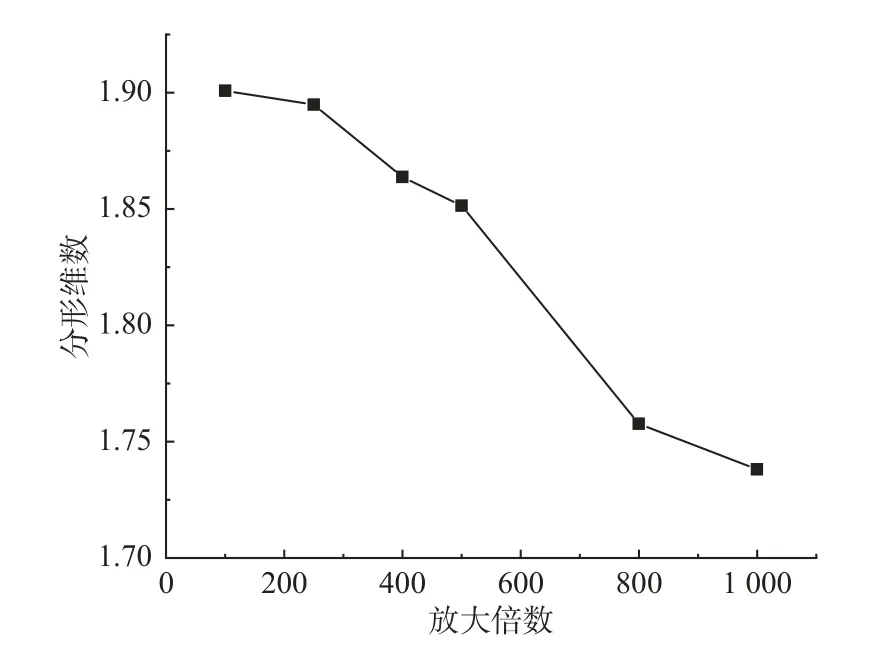
图8 分形维数与放大倍数间关系Fig.8 Relationship between fractal dimension and magnification times

图9 显示动态压缩与动态劈裂试验后的岩样断口分形维数值D均随着弹速的增大而增大。当冲击弹速为9 m/s 时，动态劈裂试验后岩样断口分形维数均值D明显高于动态压缩试验，这是由于在该弹速下动态劈裂后岩样断口与动态压缩的相比，具有更多的穿晶断裂模式，穿晶断裂往往导致岩石的碎裂度增加[6]，具体表现为分形维数值D更大。同时，动态劈裂试验拟合得到的曲线斜率大于动态压缩试验拟合得出的曲线斜率，表明动态劈裂后试样的分形维数值D率敏感性高，具体分形维数值见表2。