大数据处理中基于多任务学习的交通预测框架
2022-05-23殷正坤
殷正坤,李 鹏
(1.长沙职业技术学院 经贸与信息技术学院,湖南 长沙 410217; 2.湖南中医药大学 信息科学与工程学院,湖南 长沙 410208)
0 引 言
交通预测[1,2]在路线导航、交通管制和城市规划等很多方面都有重要的应用,已引起业界和学术界的广泛关注。人们已经提出了多种方法来求解交通预测问题,例如时间序列方法[3,4]、聚类方法[5]和机器学习模型[6-8]等等。这些方法独立地从一个传感器上提取训练数据,然后学习每个传感器的预测模型,并没有利用到多个传感器之间在交通预测上所具有的共性。还有一些研究[9,10]根据传感器的空间接近度或潜在空间中的相似性对传感器进行分组来找到多个传感器之间的共性以进行交通预测,然而它们都不能区分潜在的不同交通情况。
此外,即使对于一个单一的传感器,大量的交通状况会导致交通拥堵,比如反复出现的交通状况(比如每天的交通拥挤时间)、偶尔出现的交通状况(比如雨天)、不可预测的交通状况(比如交通事故),以及暂时性的交通拥挤(比如一场篮球赛)等,所以交通预测也会变得非常复杂。因此,单个模型难以捕获所有这些复杂的交通情况。很少有研究为不同的交通情况建立不同的模型,例如文献[11]在正常交通条件下使用差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)模型,但在交通高峰时间使用历史平均模型(historical average model,HAM)进行交通预测;文献[12]使用两种不同的深度学习模型来预测交通高峰时段和事故后的拥堵。然而,他们的研究忽略了一个事实:在一种情况下表现相同的传感器在另一种交通情况下可能会表现不同,例如,在“正常情况”下,传感器x可能与传感器y分在同一组,但在“交通高峰时段”下它又会与传感器z分为一组。
总的来看,目前还没有一种全面的交通预测方法能为所有交通状况下的所有传感器建立一个模型。一个传感器内的交通数据可能是多种交通情况的混合,因此难以构建单个模型来捕获所有这些交通状况。另一方面,本文通过处理大量的交通传感器数据发现传感器之间存在很多的共性,特别是它们在相同的交通情况下表现出相似的模式,例如在交通高峰时段或在下雨天。此外,交通情况的数量是有限的,这有助于对每种交通情况而不是对每个传感器建立一个模型。为此,文中提出一种基于多任务学习(multi-task learning,MTL)[13]的交通预测模型。首先忽略潜在的交通状况,单纯地应用MTL来共同学习所有传感器的交通预测模型(称为Naive-MTL),即每个“任务”对应一个传感器(如图1所示)。
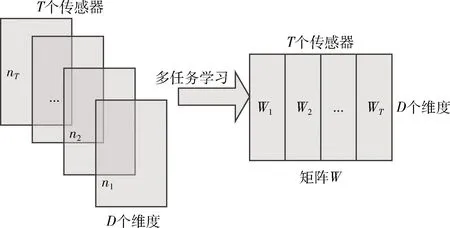
图1 简单多任务学习
然后在此基础上,本文进一步提出了一种基于情境感知的多任务学习(MTL-SA)框架:首先识别所有传感器之间的交通情况,然后对每种识别的交通状况应用MTL框架,即每个“任务”对应一种交通情况,如图2所示。
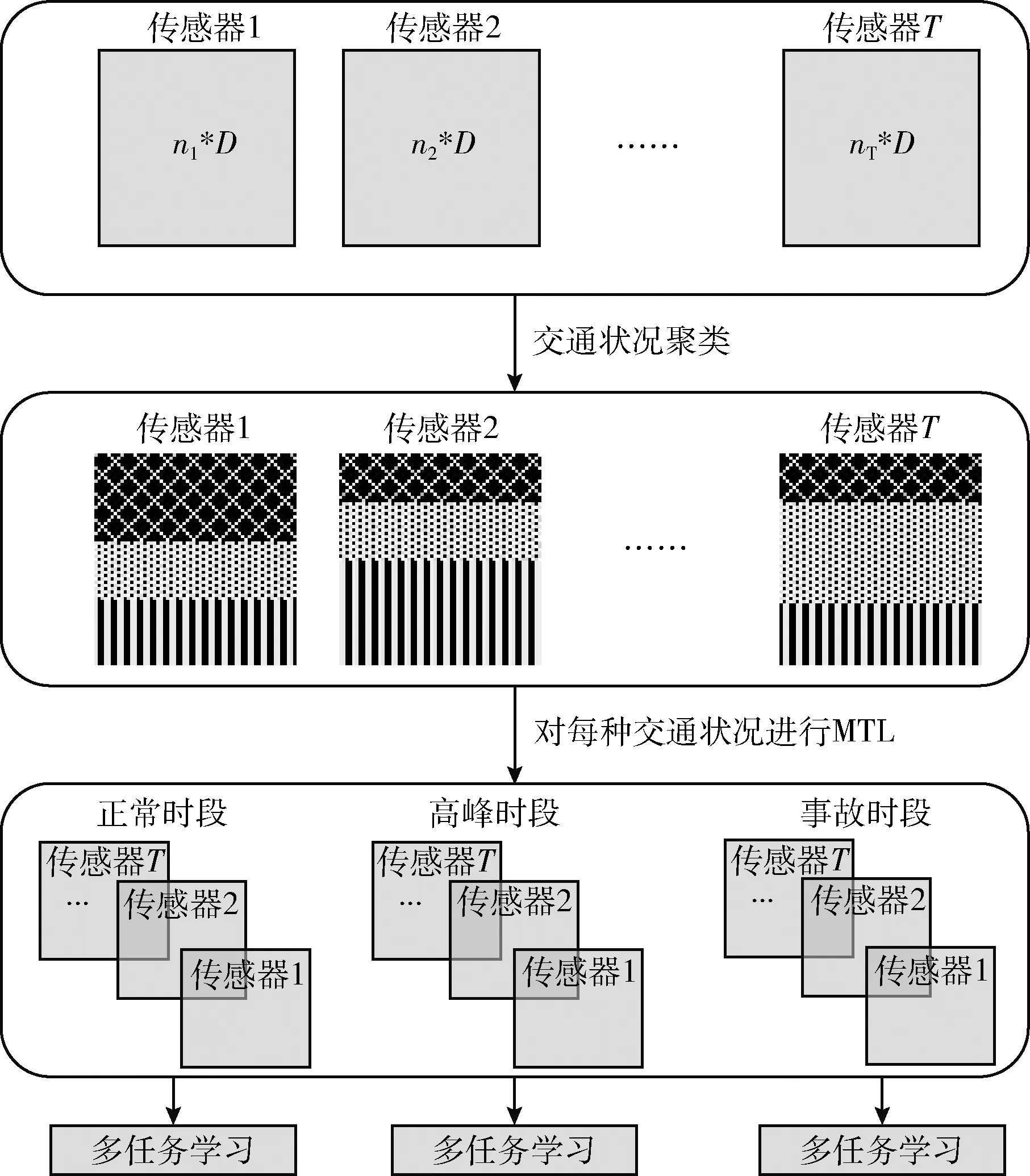
图2 MTL-SA框架
由于不同的交通情况数量很少,本文针对不同传感器的每种单独的交通情况应用MTL,以便检查是否所有传感器间共享交通情况。具体来说,为了识别交通状况,本文给一个传感器的每个训练样本增加额外的情境特征,包括道路类型(例如,公路或主干线)、位置、天气状况、区域类型(例如,商业区,住宅)和事故信息等。随后,本文结合所有传感器之间的训练样本并将它们聚集到几个分区,其中每个分区代表一种典型的交通状况。然后对于每种特定的交通情况,本文使用可以同时学习所有传感器预测模型的MTL。最后,本文利用FISTA[14]方法来解决提出的多任务学习问题,并保证收敛速度。通过对洛杉矶大规模交通传感器数据进行大量的实验来评估本文提出的模型。实验结果表明,所提出MTL-SA框架的表现不仅始终优于Naive-MTL,而且优于其它典型的交通预测方法。
1 问题建模
本节首先对交通预测问题进行了定义,然后给出了一种将多任务学习框架应用于交通预测问题的典型方法,并对该方法的性能进行了分析。为了便于描述,先给出文中用到的相关符号和说明见表1。
1.1 问题定义
给定一组包含T个交通传感器的路段,假设在给定的时间间隔γ内(例如,10分钟),每个传感器t提供交通速度读数为vt(γ) (例如,50英里/小时)。给定历史传感器数

表1 文中用到的符号和说明
据集,本文研究的目的是预测任何给定传感器在未来的交通速度。有如下的定义:
定义1 给定每个传感器t的一组观察到的历史读数,假设当前时间是γ, 交通预测问题是估计每个传感器的未来行进速度vt(γ+h), 其中h是预测范围。例如,当h=1时,本文预测下一个时间戳的交通速度。
定义2 短期预测和长期预测分别指h=1和h>1时的情景。
交通预测问题属于典型的回归问题。对于每个传感器t, 假设当前时间为γ, 为了预测vt(γ+h), 本文主要提取先前的滞后(lag)读数(即vt(γ-1),vt(γ-2), …,vt(γ-lag)) 作为训练特征。对于每个传感器t, 本文构造训练输入xt和输出yt, 其中xt∈Rnt×D,yt∈Rnt,D是特征的数目,本文的目标是训练得到一个线性函数f, 其中ft(xt)=xtwt和wt∈Rd×1。 为了学习参数向量wt, 本文解决以下的优化问题
(1)
其中,l(ft(xt),yt) 用来定义损耗函数, Ω(wt) 是每个传感器的正则化项。例如,本文可以分别采用平方损失和l2的正则化。本文的目标是学习每个传感器T的线性模型。本文将W=[w1,w2,…,wT]∈RD×T表示为要估计的参数矩阵。
1.2 简单多任务学习
本文首先采用典型的多任务学习来共同学习所有传感器的预测模型,而不是单独解决每个任务。本文通过提取和利用这些传感器的公共信息来同时学习所有预测任务。如图1所示,估算W的一种典型MTL过程如下

(2)

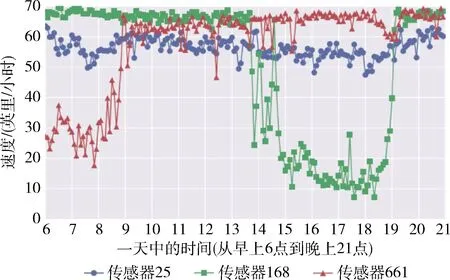
图3 3个不同高速公路传感器在同一天的交通读数
2 MTL-SA框架
MTL-SA首先将所有传感器的训练样本组合在一起,并将它们分类成几个分区,其中每个分区代表一种典型的交通状况,并由来自所有传感器的不同数量的训练样本组成。然后,对于每个分区而言(即交通状况),本文使用多任务特征学习来同时得到所有传感器的预测模型。下面对其细节进行详细阐述。
2.1 总体框架
虽然每个传感器都有其独特的交通模式,但它们在相同的交通情况下(例如,正常或交通高峰时段条件)表现出相似的性能,如图3所示。假设传感器在通常交通情况下表现相似,这激励本文在每种交通情况下探索传感器之间的共性。为此,本文提出了情境感知多任务学习框架(MTL-SA),如图2所示。在MTL-SA中,本文首先通过聚类算法识别所有传感器的交通情况,然后对每种交通状况应用传统多任务学习框架进行交通预测,具体步骤如算法1所示:①将来自所有传感器的训练样本组合在一起(第(1)~第(3)行);②将组合的训练数据分类为k个分区,其中每个分区由来自不同传感器的训练样本构成(第(4)行);③对每个分区Pc应用多任务学习,其中c∈[1,k], 并对每种交通情况学习每个参数矩阵Wc(第(5)~第(7)行)。利用每个分区Pc的训练模型Wc, 本文能够在任何情况下对任何传感器进行流量预测。给定来自具有输入特征的一个传感器的预测请求,本文首先确定该请求的潜在流量情况(即,聚类标签c)。然后利用基于Wc的训练模型来预测其未来的行进速度。
算法1:MTL-SA框架
输入: ∀t∈[1,T],xt∈Rnt×D,yt∈R, 聚类数量k
输出: ∀c∈[1,T],Wc
(1) Fort=1 toTdo
(2)X←∪xt//见2.2节
(3) End
(4) 将X分成簇Pc(c (5) Forc=1tokdo (6) 针对每种交通情况Pc的多任务学习Wc//见2.4节 (7) End 本文对矩阵X进行聚类以识别隐藏的交通情况。具体而言,本文将训练数据分成不同的组,其中每组对应一种交通情况。一个直截了当的想法是使用传统的聚类方法(如K均值[15])并指定聚类的数量。但在本文的交通预测问题中,本文的目的是发现传感器的潜在相似性,即潜在的交通模式。由于不同交通情况的密度可能会不同(例如,正常交通状况在训练样本中占主导地位),K均值聚类可能表现不佳。因此,本文提出利用非负矩阵分解(non-negative matrix factorization,NMF)[16]来发现交通状况。形式上,给定输入矩阵X∈RN×D和聚类数量k, 其中k (3) (4) (5) 2.4.1 问题求解 (6) 给定当前搜索点Wi, FISTA算法首先求出f(W) 在点Wi处的二次近似Q来生成下一个点Wi+1。 二次近似函数Q(W,Wi) 在Wi处的定义如下所示 (7) (8) 除了使用一个序列 {Wi} 之外,FISTA还使用了另外一个序列 {Zi}, 其中 {Wi} 是近似解的序列, {Zi} 是搜索点序列。在搜索点Zi处生成Wi+1的近似解,并且Zi是Wi-1和Wi的仿射组合。算法2中给出了FISTA算法的细节。在每次迭代中,本文首先从Wi和Wi-1(第(4)行)生成Zi的搜索点,并从Zi的搜索点(第(7)行)计算Wi+1。 最后,根据Armijo规则[18],通过线搜索计算每一步的步长η。 算法2:FISTA算法 输入: ∀t,xt,ytandW0 输出:W (1) 初始化W1=W0,λ-1=0,λ0=1,η=1; (2) fori=1,2,…, do (4)Zi←(1-αi)Wi+αiWi-1; (5) forj←0,1,… do (6)η←2jηi-1; (8) ifF(Wi≤Q(Wi,Zi)) then (9)ηi←η; (10) break; (11) end (12) end (14) if Convergence then (15)W←Wi; (16) break; (17) end (18) end 2.4.2 时间复杂度分析 本文进行了丰富的实验来评价MTL-SA框架的有效性和效率。先将MTL-SA框架与各种基线方法进行了比较,然后展示了改变不同参数的效果。最后,本文提供了实例研究来验证MTL-SA框架的优势。 3.1.1 数据集 本文使用了大量的来自洛杉矶高速公路和主干道的高分辨率(空间和时间)交通传感器(环路检测器)收集的数据集。该数据集包括15 000个交通传感器的库存和实时数据,大约覆盖3420英里。数据的采样率为每分钟每个传感器读取一个数值。传感器的数据聚合为5分钟一个间隔。本文选取了从2019年1月至2019年4月共计880个传感器的4个月收集的数据进行实验。 3.1.2 对比算法 本文将MTL-SA框架与以下基线方法进行了比较: (1)几乎不需要训练的方法:历史平均模型(HAM)[11]、随机游走(RW)(即,使用最近的读数作为预测速度)。 (2)单一传感器模型:岭回归模型(Ridge)[19]、支持向量回归(SVR)[20]、多层神经网络(Neural)[21]、随机森林(Forest)[19]和时间序列方法差分整合移动平均自回归模型(ARIMA)[11]。 (3)多传感器模型:不考虑交通状况的多任务特征学习模型(MTFL)[22]和聚类多任务学习模型(CMTL)[23]。 3.1.3 实验过程和配置 对于每个传感器t, 本文从其历史数据集生成训练样本和测试样本:假设当前时间为γ, 为了预测v(γ+h), 本文主要利用先前传感器读数的信息,即v,vt(γ-1),vt(γ-2), …,vt(γ-lag) 作为本文的特征。本文测试了不同的lag值,发现当将lag固定为6时,在准确性和训练复杂度之间实现了较好的平衡。此外,本文还生成了历史特征:即对于一个传感器的每个工作日时间(例如周一下午4点),本文汇总了该传感器在过去3个月(一月至三月)的特定时间内的先前读数。除了来自传感器读数的特征,本文的训练特征还包括基本情境信息(例如,一天中的时间、一周中的某一天)和传感器属性(例如,传感器的分类、方向)。本文使用了两个月的数据,其中3月份的数据用于训练,4月份的数据用于测试。在本文的实验中,本文没有将天气和事件数据作为训练特征,本文在除ARIMA外的所有模型中应用了相同的特征,因为ARIMA是一个单变量时间序列方法。对于ARIMA,本文只使用3月份的数据进行训练,使用4月份的数据进行测试。 本文使用均方根误差(RMSE)来衡量精度。本文人工区分高峰时段(即早上7点到9点,下午4点到7点)和非高峰时段范围,报告了它们的RMSE,并且分别进行了短期和长期的交通预测,其中h=1 (即5 min)为短期预测,h=6 (即30 min)为长期预测。RMSE的定义如下所示 (9) 对于每一种测试方法,本文都使用5折交叉验证来选择最佳参数,并报告相应的结果。本文在一台Linux PC上进行了实验,CPU为i5-2400@ 3.10 G HZ,内存为24 GB。 (1)短期交通预测:表2给出了当h=1时的性能比较,即本文预测未来5 min的交通状况。在所有方法中,MTL-SA与高峰时段和非高峰时段的基线方法相比,性能分别提高了18%和13%,达到了最佳。因为高峰时段的交通状况预测更复杂,所以高峰时段的预测误差高于非高峰时段。本文清楚地观察到,通过结合交通情况,MTL-SA的表现明显优于Naive-MTL。即使是非高峰时段,由于其重复模式已经准确预测了非高峰时段的短期交通状况,因此预测误差减少了13%。另一方面,Naive-MTL的性能与其它单一传感器模型(例如,Ridge、SVR)类似。可以独立地为每个传感器训练模型,简单地将传感器分组而不考虑交通状况的CMTL甚至比Naive-MTL的性能更差。这些观察结果支持了本文的假设,即将传感器分组在一起而不考虑它们在不同交通情况下的共性,这对于交通预测没有影响甚至是负面的影响。在其它基线方法中,RW实现了良好的性能(甚至优于其它单一传感器模型)而HAM表现更差,这表明最近的读数是短期预测的一个强有力指标,而历史特征却不起任何作用。在单个传感器模型中,Ridge、Neural和SVR取得类似的结果,而Forest在其中表现最差。 表2 短期预测性能(RMSE) (2)长期交通预测:在表3中给出了长期预测的实验结果,本文用它来预测接下来30分钟的交通状况(即h=6)。从表3可以看到,与每种情况的最佳基线相比,MTL-SA的预测精度都至少提高了30%以上。同时,MTL-SA比Naive-MTL和CMTL表现更好,这表明在识别交通情况后探索共性更有效。值得注意的是,HAM和RW等简单方法不再适用于长期预测,因其预测性能比单一传感器模型差得多。对于单一传感器模型,SVR比Ridge、Neural和Forest表现更好。 表3 长期预测性能(RMSE) (3)运行时间比较:表4给出了在训练和测试阶段不同方法的运行时间。在所有单一传感器模型中,Ridge是最有效的,因为它是线性模型,而其它非线性模型(如Neural、Forest和SVR)需要更多的训练时间。另一方面,作为多传感器模型,MTFL需要与Ridge类似的训练时间。与Ridge和RW相比,本文的方法MTL-SA需要更长的时间,因为本文需要额外的步骤来识别交通状况,然后对每个已识别的情况应用MTL。然而,即使包括额外的步骤,MTL-SA的训练时间仍然有效并且花费不到70 s,因此它可以很容易地扩展到大量传感器。 表4 不同方法运行时间的比较 (1)使用历史特征的影响:本文评估了使用不同训练特征集的效果,图4给出了有/无历史平均速度读数的交通预测结果。如图4(a)所示,历史聚集的平均读数对短期预测没有任何帮助,这与表2中的结果是一致的:HAM的精度最差,反而RW具有相对较好的性能。但是,如图4(b)所示,历史特征也无助于长期预测。这与本文的常识-历史平均值可以作为长期预测的良好预测因子相矛盾。原因在于,根据本文的观察,历史数值反映了在大多数过渡时间地面真实数值的趋势(即高峰时段的边界),但与其它交通条件下的读数没有关系。此外,交通预测任务由那些非转换时间的实例所支配,因此历史特征在长期预测中没有多大帮助。图5(a)和图5(b)显示了在非高峰时段类似的影响。 图4 使用历史特征对高峰时段的影响 图5 使用历史特征对非高峰时段的影响 (2)变化的k的影响:不同聚类算法结果(NMF与K均值)和不同的聚类数量k(即交通情况)对于交通预测的影响如图6(a)和图6(b)所示。可以看到,NMF和K-means获得了类似的结果,NMF的表现略好于K-means。这表明了NMF在发现潜在交通情况方面的优越性。对于聚类的数量k而言,本文注意到k=4时,MTL-SA无论是做短期还是长期交通预测都达到了最佳性能。这表明即使交通状况混乱且复杂,本文仍然可以通过有限数量的交通情况来区分其潜在的分组,这是MTL-SA框架在交通预测任务中有效和高效的主要原因之一。 图6 变化的k对高峰时段和非高峰时段的影响 图7 变化的ρ1对高峰时段的影响 (3)式(5)中变化ρ1的影响:图7(a)和图7(b)显示了ρ1从0.0001变化到1000时对于交通预测的影响。本文观察到当ρ1=1时,MTL-SA达到最佳的RMSE值。当ρ1变得越大时,性能较差。因此,将ρ1设置为较小的值(例如,1)可以得到更好的准确度。 最后,以洛杉矶某一主干道的交通实况作为监测环境,主要考虑了对于最难预测的交通高峰过渡时段,模拟事故模式和其它突发情况等监测对象,以标号为168的传感器监测数据为例,图8给出了MTL-SA的预测值与最佳基线方法、地面真实交通情况的对比结果,以验证MTL-SA在各种交通情况下的优越性。从图中可以看到,与最佳基线方法相比,本文方法的预测结果在过渡时间有较小的误差,特别是在[12 pm,13 pm]和[18 pm,19 pm]的范围内,而最佳基线方法无法捕捉到这些突然的变化。此外,与地面真实交通情况相比,MTL-SA基本可以做到准确地拟合,这表明了MTL-SA在真实环境中进行交通预测的有效性,可以应用到大规模交通网络中去。 图8 h=6时,传感器168的实测结果 文中提出了一种多任务学习框架(MTL-SA)用于预测交通问题。与现有的每个传感器训练一个模型的MTL规则不同,本文提出的框架自动识别基本交通情况,同时根据每种交通情况训练一个模型。通过大量的实验评估发现MTL-SA框架可以准确地捕获交通状况,并能显著改善短期和长期的交通预测,特别是对长期的交通预测更加明显。在下一步工作中,本文进一步分析影响短期和长期交通状况的因素,并借鉴图卷积神经网络在处理复杂交通网络上的优势,拟提出一种基于图卷积神经网络的交通预测算法。2.2 训练数据的整合和增强
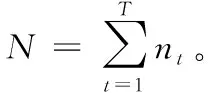
2.3 交通状况聚类
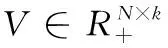
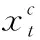
2.4 每个交通状况的多任务学习
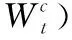

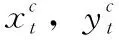


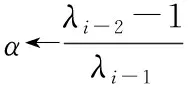
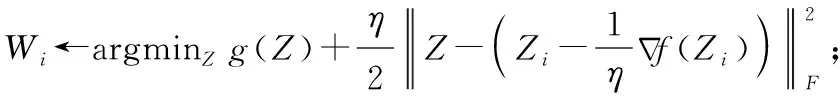
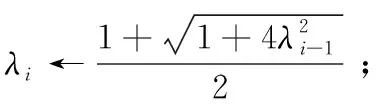
3 仿真实验
3.1 实验设计
3.2 性能比较
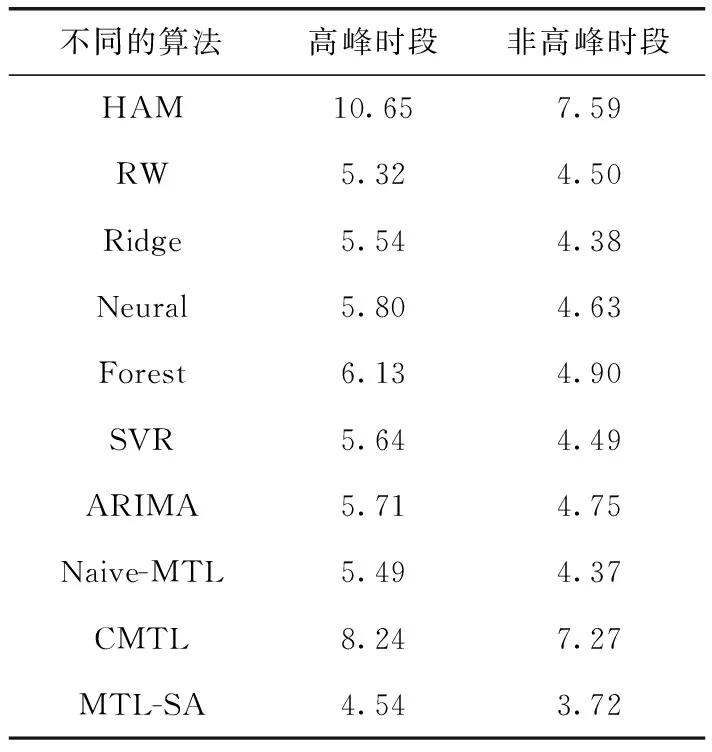
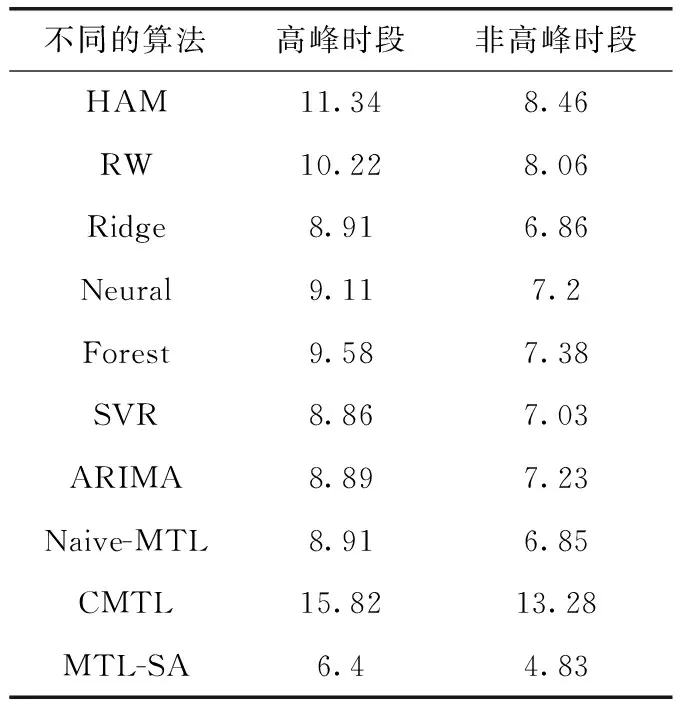
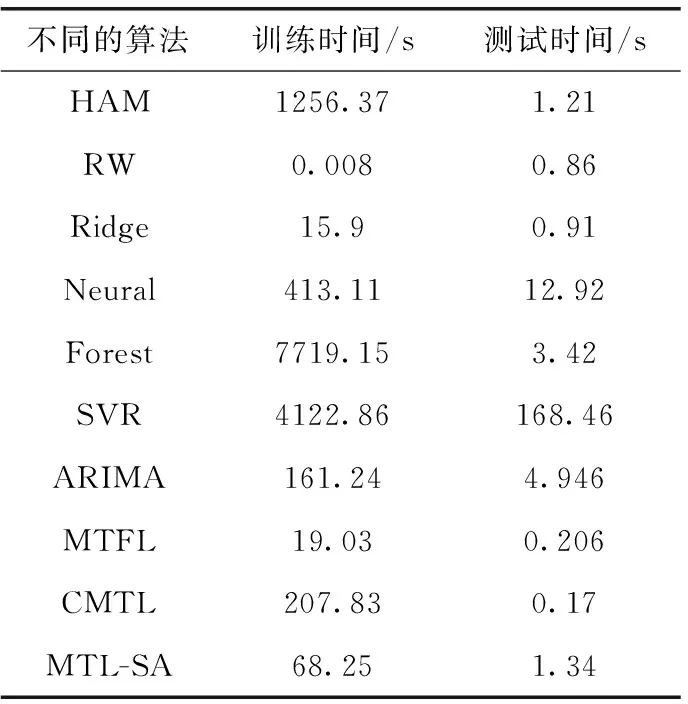
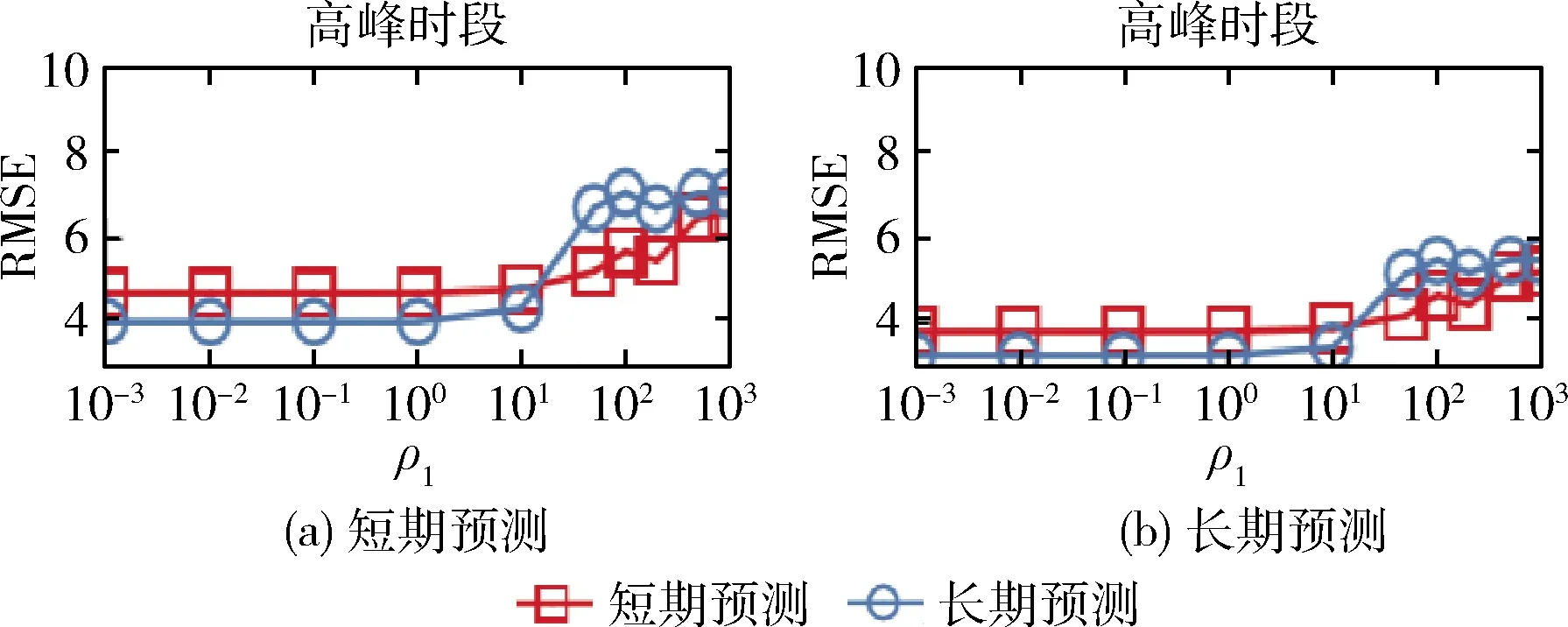
3.3 不同参数条件下的预测性能分析


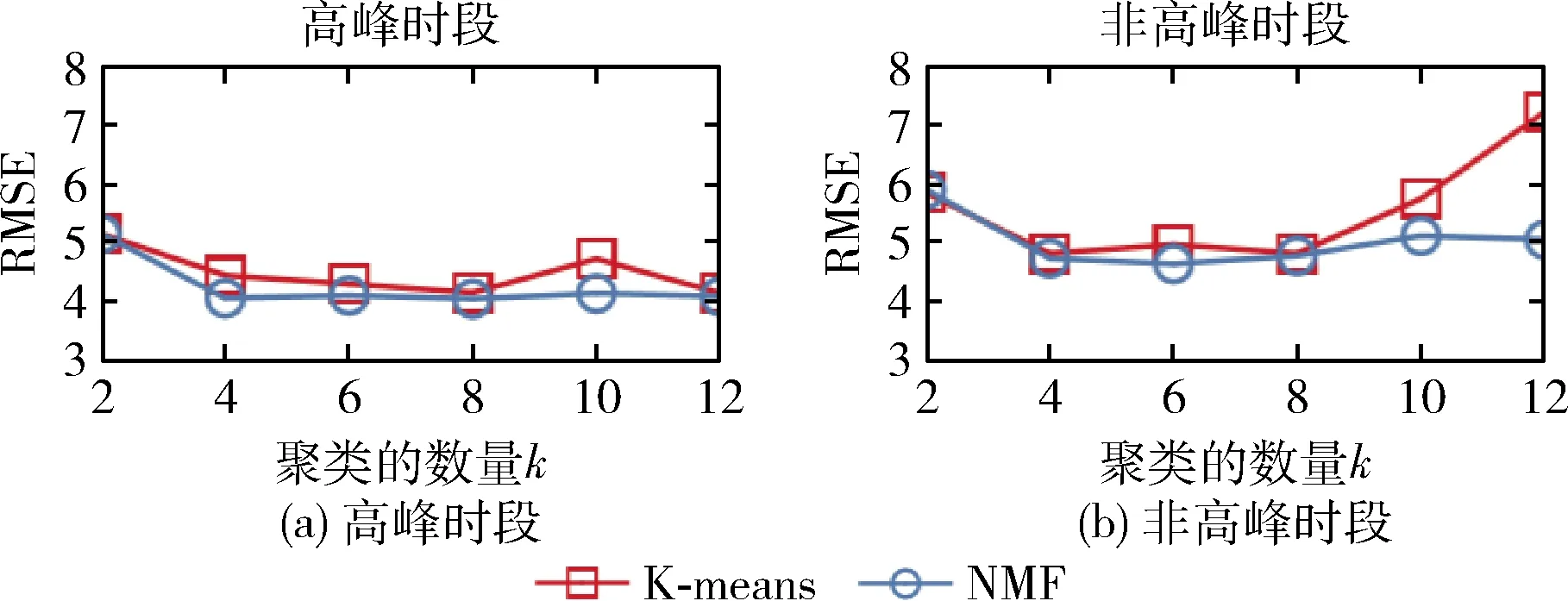
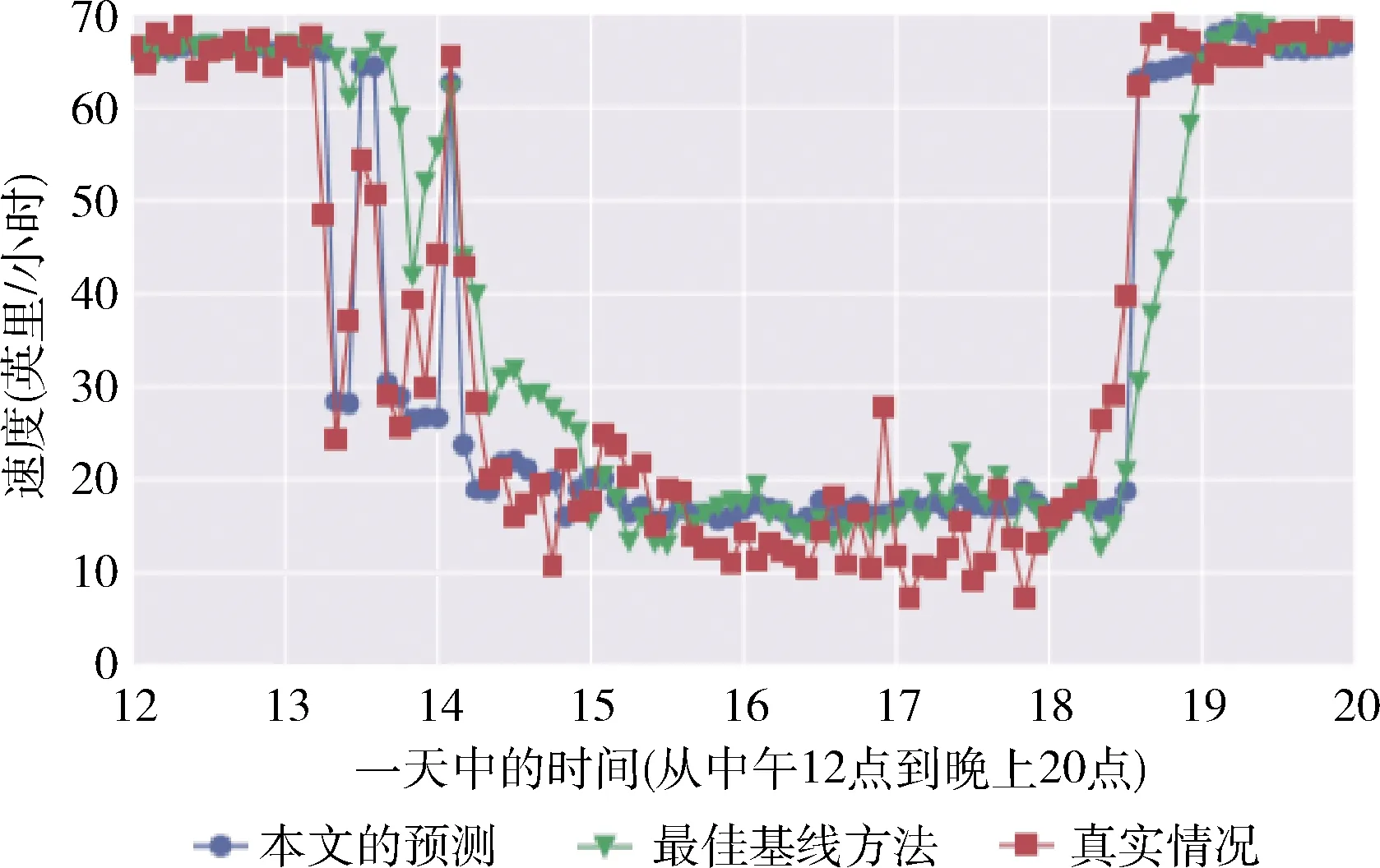
3.4 交通预测实例分析
4 结束语
