基于多窗口联合优化的多次波自适应相减方法

孙宁娜,曾同生,戴晓峰,周润庚,李钟晓,李振春,盛冠群

(1.青岛大学电子信息学院,山东青岛266071;2.中国石油勘探开发研究院,北京100083;3.中国石油大学(华东)地球科学与技术学院,山东青岛266580;4.三峡大学大数据中心,湖北宜昌443000)

在地震数据常规处理中,多次波被视为一种干扰噪声,它们的存在会干扰对一次波的处理。因此,需要尽量在地震数据叠前处理阶段对多次波进行压制。压制多次波的方法主要有滤波法[1-2]和基于波动方程的预测相减法[3-8]。滤波法是基于信号分析处理的方法,利用一次波和多次波之间的特征或性质的差异压制多次波[9]。但对于复杂地质构造,基于波动方程的预测相减法进行多次波压制的效果更加显著。该方法是采用数据驱动或模型驱动的方式构造多次波模型,然后利用自适应相减方法压制多次波[10]。其关键步骤为多次波自适应相减,其效果的优劣决定着多次波压制的精度,进而影响地震数据成像和反演的效果。

多次波自适应相减方法主要包括基于匹配滤波器的方法[11-13]、基于模式识别的方法[14-16]、基于盲信号分离的独立成分分析法[17]、基于支持向量回归的方法[18]、基于卷积神经网络的方法[19]和基于U-net的方法[20]。基于匹配滤波器的方法被归结成一个线性回归问题,利用匹配滤波器消除预测多次波与真实多次波之间的复杂差异,在业界被广泛应用。VERSCHUUR等[21]使用1D匹配滤波器表示预测多次波与真实多次波的差异,在2D时间-空间数据窗口内对估计一次波施加能量最小化约束,并利用最小二乘算法求解1D匹配滤波器。考虑到预测多次波和实际多次波在空间上也存在差异,DONNO[22]将1D匹配滤波器扩展到时间-空间域的2D匹配滤波器,获得了比1D匹配滤波器更好的多次波自适应相减结果。李钟晓等[23]将多次波自适应相减表示为一个2D卷积信号盲分离问题,以2D匹配滤波器表示真实多次波与预测多次波之间的差异,采用一次波的非高斯性最大化为优化目标,并利用迭代最小二乘算法(IRLS)[24]求其优化问题。但由于IRLS在每次迭代中都需要解决一个最小二乘优化问题,使得该方法计算效率较低。LIU等[25]构建一次波L1范数最小优化问题,并使用迭代收缩阈值算法(ISTA)[26]加速求解2D匹配滤波器。快速迭代收缩阈值算法(FISTA)[27-28]是ISTA的加速版本,在每一步迭代中,FISTA通过线性组合当前和先前步骤中的收缩阈值结果来获得更新的收缩阈值结果,可以达到更高的精度和计算效率。LI等[29]在抛物线Radon域将多次波自适应相减表示为2D匹配滤波器求解的问题,构建基于一次波L1范数最小化约束的优化问题,并采用FISTA来求解该优化问题。

考虑到地震数据的非稳态性,在多次波自适应相减过程中需要将地震数据进行分窗。当采用较大的数据窗口时,需要选择较大的匹配滤波器去压制多次波。但对于较大的数据窗口,求取匹配滤波器时需要构造较大的数据褶积矩阵进行求逆操作,这会导致较低的计算效率。当采用较小的数据窗口时,由于数据窗口的大小限制,匹配滤波器的尺寸不能过大。而由于预测多次波和真实多次波在时间、空间和振幅上通常存在较大的差异,单个小窗口匹配得到的短滤波器很难准确地表征预测多次波与真实多次波之间的复杂差异,往往会造成多次波残余和一次波损伤。

本文提出基于多窗口联合优化的多次波自适应相减方法,该方法可以同时利用多个小数据窗口中丰富的预测多次波信息,将多个窗口的预测多次波和对应的原始数据进行拟合来压制多次波。该方法对多个窗口中的一次波施加L1范数最小化约束,并利用快速迭代收缩阈值算法(FISTA)求解该优化问题。首先介绍了基于多窗口联合优化的数学模型;然后在构建多窗口L1范数最小化优化问题的基础上,详述了FISTA迭代步骤;最后将基于多窗口联合优化的多次波自适应相减方法应用于模型数据和实际数据,以验证方法的有效性。

1 基于多窗口联合优化的数学模型

基于单窗口匹配的数学模型为[25,27,29-30]:

p=s-Mx

(1)

式中:p表示估计一次波构建的向量,大小为TR×1(TR=T×R);s表示原始数据构建的向量,大小为TR×1(TR=T×R);M表示预测多次波构建的褶积矩阵,大小为TR×pq(TR=T×R,pq=p×q);x表示匹配滤波器,大小为pq×1(pq=p×q)。T和p为采样点个数,分别表示2D处理窗口的时间大小和匹配滤波器的时间长度;R和q为道数,分别表示2D处理窗口空间大小和滤波器的空间长度。

本文引入多窗口联合优化求解匹配滤波器,同时利用多个窗口的预测多次波信息来实现多次波自适应相减。基于多窗口联合优化的数学模型可以表示为:

vi=di-Hix(i=1,2,…,n)

(2)

式中:vi(i=1,2,…,n)表示第i个窗口中估计一次波构建的向量,大小为TR×1;di(i=1,2,…,n)表示第i个窗口中原始数据构建的向量,大小为TR×1;Hi(i=1,2,…,n)表示第i个窗口中预测多次波的褶积矩阵,大小为TR×pq;n表示同时进行优化的窗口个数。

输入n个窗口的原始数据和预测多次波同时进行优化,在n个重叠的二维数据窗口上估计一个匹配滤波器。由于利用了多个数据窗口丰富的预测多次波信息,基于多窗口联合优化的匹配滤波器可以更有效地消除真实多次波与预测多次波之间的复杂差异。

2 优化问题

求解匹配滤波器x的关键是使预测多次波经过x滤波后与真实多次波之间的差异达到最小[23]。传统的基于单窗口匹配的多次波自适应相减方法是在每一个2D窗口上求解一个匹配滤波器,在每个窗口中基于一次波L1范数最小化约束求解匹配滤波器系数。相应的优化问题表示为:

(3)

式中:加权因子α用来均衡一次波稀疏约束和滤波器系数能量最小化约束。为更好地保护一次波并压制多次波,本文构建如下的优化问题:

(4)

本文构建的优化问题利用了多个窗口的预测信息,目的是使多个窗口的一次波L1范数同时最小化。与构建单个窗口的一次波L1范数最小化相比,多个窗口联合的一次波L1范数最小化可以防止过拟合,在压制残余多次波的同时,有效地保护一次波。

3 求解算法

本文采用FISTA求解优化问题(4)中的匹配滤波器。FISTA在估计一次波时定义如下的距离算子:

(5)

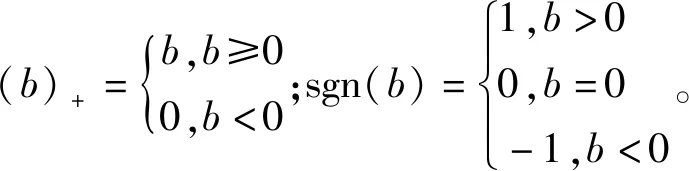
FISTA通过线性组合当前和先前步骤中的收缩阈值结果来获得更新的收缩阈值结果。在本文中,使用FISTA获得更新的收缩阈值结果:

i=1,2,…,n

(6)

(7)

然后,估计一次波为:

(8)

因此,可将FISTA步骤总结如下。

对于迭代次数m=0,1,…,N-1:

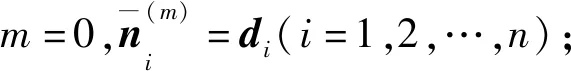
4)m=m+1,若m未达到最大迭代次数N,返回步骤1)计算更新的收缩阈值;否则,停止迭代。

本文将FISTA进行了推广,当同时优化的窗口个数n=1,利用FISTA求解优化问题(4)中的匹配滤波器,在每次迭代时,只需计算一次更新阈值。但当同时优化的窗口个数n>1,FISTA在求解匹配滤波器时,需要计算n次更新阈值。本文基于推广的FISTA求解得到的匹配滤波器利用了n个数据窗口的预测多次波信息,可以更有效地表征预测多次波和真实多次波之间的差异。

4 应用实例

4.1 模型数据

模型数据包含195道,每道包含900个采样点,采样率为8ms。图1a和图1b分别是原始数据和2D自由表面多次波压制方法(surface related multiple elimination,SRME)[31]预测的自由表面多次波。针对本文所提方法,选择同时优化的窗口个数n=280;匹配滤波器在时间方向上的长度p=7,在空间方向上的长度q=5;数据窗口在时间方向上的长度T=60、在空间方向上的长度R=50。因此,用280个预测多次波窗口匹配280个原始数据窗口,并可同时输出280个窗口的一次波估计结果。另外,选取一次波阈值sγ=0.2、阻尼因子α=0.001、最大迭代次数M=5。

图1 原始模型数据(a)和预测的自由表面多次波数据(b)

为了定量评价本文所提多次波自适应相减方法的性能,定义如下的信噪比:

表1 模型数据的运行时间和信噪比

(9)

其中,p0表示真实一次波,p表示估计的一次波。图2a,图2b和图2c分别表示本文方法估计的一次波、去除的多次波和差剖面。其中,差剖面定义为真实一次波与一次波估计结果差值的绝对值。本文方法估计一次波的SNR为20.45dB,见表1所示。

基于多窗口联合优化的多次波自适应相减方法基于单窗口匹配的多次波自适应相减方法(小窗口)基于单窗口匹配的多次波自适应相减方法(大窗口)运行时间/s0.640.702.88SNR/dB20.4514.4519.98

传统基于单窗口匹配的方法首先选择较小的2D数据窗口,匹配滤波器在时间方向上的长度p=5、在空间方向上的长度q=3,数据窗口在时间方向上的长度T=70、在空间方向上的长度R=60,一次波阈值sγ=0.1,阻尼因子α=0.001,最大迭代次数N=6。图3a显示了基于单窗口匹配的多次波自适应相减方法(选取较小的2D数据窗口)得到的一次波估计结果。图2a和图3a中的黑色箭头所示表明,相对于传统的小窗口匹配方法,本文采用多窗口联合优化方法在一次波估计结果中能更有效地去除残余多次波。此外,图3a中的一次波SNR为14.45dB。相比而言,本文方法所得到的一次波信噪比提高了6dB。图3b显示了基于单窗口匹配的多次波自适应相减方法(选取较小的2D数据窗口)所去除的多次波。图2b和图3b中的白色箭头所示表明,基于多窗口联合优化的多次波自适应相减方法能更好地保护一次波。差剖面可用于评估多次波是否被有效去除以及一次波是否被很好地保护。图3c为基于传统的小窗口匹配得到的差剖面。对比图2c与图3c可见,图2c中的能量明显少于图3c。说明本文方法能更有效地分离一次波和多次波。

图2 基于多窗口联合优化的模型数据实验a 一次波估计结果;b 去除的多次波;c 差剖面

另外,选择较大的2D数据窗口,数据窗口在时间方向上的长度T=193、在空间方向上的长度R=248,匹配滤波器在时间方向上的长度p=11,在空间方向上的长度q=9,其它参数(一次波阈值、阻尼因子、最大迭代次数)与图3a中的对应参数取值相同。图4a为基于大数据窗口匹配的传统多次波自适应相减方法得到的一次波估计结果;图4b为去除的多次波。图4a中的一次波SNR为19.89dB(表1)。虽然图4a的SNR与本文方法接近,但计算效率低于本文方法,本文方法的运行时间为0.64s,传统基于单窗口匹配方法(小窗口、大窗口)的运行时间分别为0.70s和2.88s(表1)。图4c为基于传统的大数据窗口匹配得到的差剖面。因此,针对模型数据处理结果,相对于选取较小数据窗口的传统的多次波自适应相减方法,本文方法在去除残余多次波的同时能更好地保护一次波,并且一次波信噪比提高了6dB。相对于选取较大数据窗口的传统的多次波自适应相减方法,本文方法在保持计算精度的基础上,计算效率提高了约78%。

图3 基于单窗口匹配的模型数据实验(小窗口)a 一次波估计结果;b 去除的多次波;c 差剖面

图4 基于单窗口匹配的模型数据实验(大窗口)a 一次波估计结果;b 去除的多次波;c 差剖面

为了分析本文方法中窗口匹配个数对一次波与多次波分离效果的影响,对模型数据进行了进一步的实验。

选择不同的窗口匹配个数,其它参数(数据窗口大小、滤波器长度、一次波阈值、阻尼因子、最大迭代次数)与图2a中的对应参数取值相同。图5给出了一次波信噪比随窗口匹配个数的变化曲线。由图5可见,在窗口匹配个数为280时得到的信噪比最高,为20.45dB。

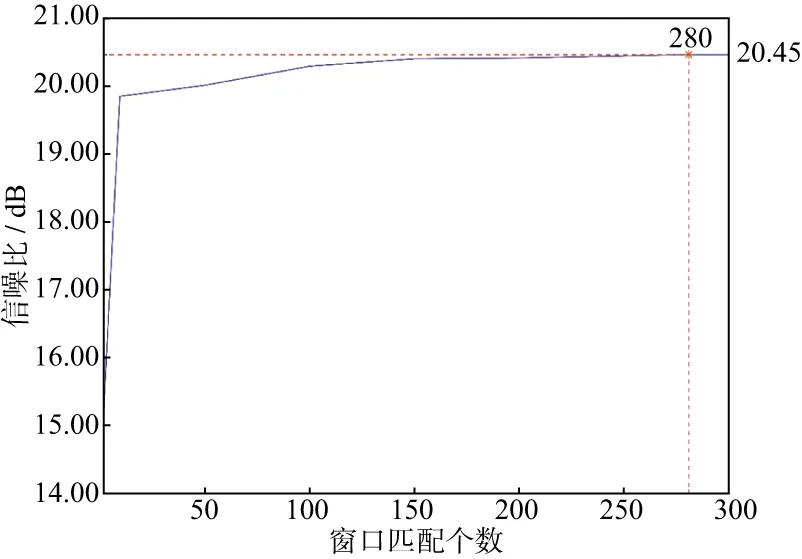
图5 模型数据的一次波信噪比随窗口匹配个数的变化曲线

此外,为了分析本文方法中窗口匹配个数对计算效率的影响,选择了几个典型的窗口匹配个数对模型数据进行了实验。

选择窗口匹配个数n=2时,运行时间为0.88s;选择窗口匹配个数n=30时,运行时间为0.79s;选择窗口匹配个数n=150时,运行时间为0.70s;选择窗口匹配个数n=280时,运行时间为0.64s。由于选择较小的窗口匹配个数,处理所有的数据窗口需要多次对褶积矩阵进行求逆,因此会比选择较大的窗口匹配个数时计算效率低。

4.2 实际数据

本文选取316个采样点(160～792ms)、道数为493的共偏移距道集来验证基于多窗口联合优化的多次波自适应相减方法的效果。图6a为原始数据,图6b为2D SRME方法预测的自由表面多次波。从图6a中可以看出,多次波的能量强且分布广泛,存在强同相轴且一次波与多次波相互重叠。与图6a相比,图6b的预测多次波与真实多次波存在较大的振幅差异等。

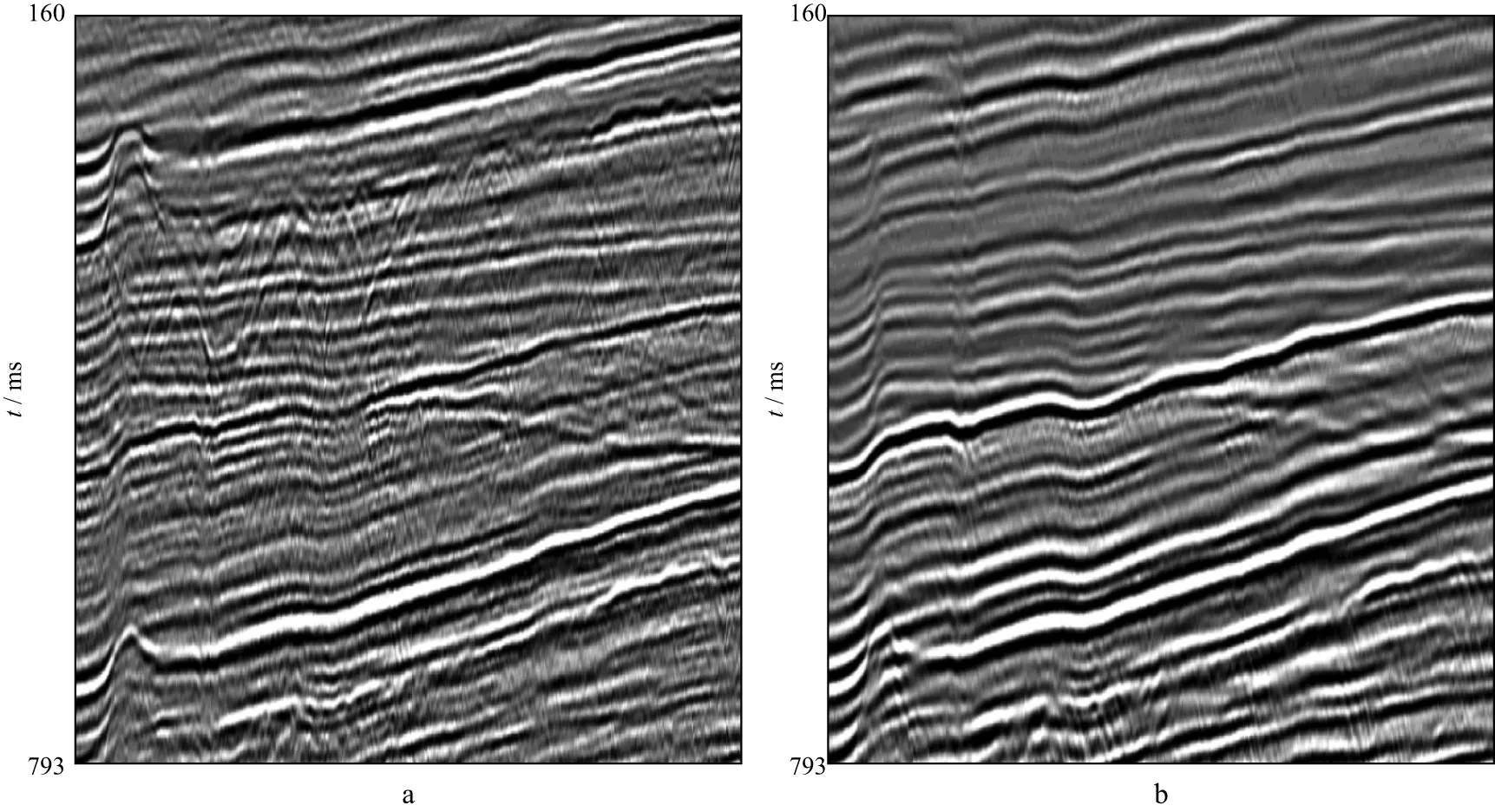
图6 实际数据中的原始数据(a)和预测的自由表面多次波(b)

针对基于多窗口联合优化的多次波自适应相减方法,选择同时优化的窗口个数n=5,匹配滤波器在时间方向上的长度p=7,在空间方向上的长度q=9,数据窗口在时间方向上的长度T=35、在空间方向上的长度R=30。因此,用5个预测多次波窗口匹配对应的5个原始数据窗口,并可同时输出5个窗口的一次波估计结果。求出的匹配滤波器能有效表征5个数据窗口中预测多次波与真实多次波之间的复杂差异。另外,选取一次波阈值sγ=0.1、阻尼因子α=0.001、最大迭代次数M=10。图7a 和图7b分别表示本文方法估计的一次波和去除的多次波。

对于传统基于单窗口匹配的方法,首先选取较小的2D数据窗口,匹配滤波器在时间方向上的长度p=5,在空间方向上的长度q=3,数据窗口在时间方向上的长度T=70、在空间方向上的长度R=70。另外,选取一次波阈值sγ=0.1、阻尼因子α=0.001、最大迭代次数M=10。图8a和图8b分别为基于小窗口的传统多次波自适应相减方法得到的一次波估计结果和去除的多次波。对比图7a和图8a中箭头处可见,本文方法比基于小窗口的传统多次波自适应相减方法能更彻底地去除多次波。

选取较大的数据窗口进行多次波自适应相减,匹配滤波器在时间方向的长度p=9,在空间方向上的长度q=11,数据窗口在时间方向上的长度T=100、在空间方向上的长度R=120。另外,选取一次波阈值sγ=0.1、阻尼因子α=0.001、最大迭代次数M=10。图9a和图9b为基于大窗口的传统多次波自适应相减方法得到的一次波估计结果和去除的多次波。由图7、图8和图9可见,相比于选取较小的数据窗口进行多次波自适应相减,选取较大的数据窗口和基于多窗口联合优化的多次波自适应相减方法可以更好地平衡一次波保护和多次波去除。但由于本文利用多窗口联合优化求解匹配滤波器,需要构建的预测多次波褶积矩阵小,从而计算效率比选取较大的数据窗口进行自适应相减高。本文所提方法的运行时间为1.46s,传统的多次波自适应相减方法(小窗口、大窗口)的运行时间分别为1.40s和2.81s,如表2所示。

图7 基于多窗口联合优化的实际数据实验a 一次波估计结果;b 去除的多次波

图8 基于单窗口匹配的实际数据实验(小窗口)a 一次波估计结果;b 去除的多次波

图9 基于单窗口匹配的实际数据实验(大窗口)a 一次波估计结果;b 去除的多次波

因此,针对实际数据处理结果,相比选取较小数据窗口的传统多次波自适应相减方法,本文方法可以更好地去除残余多次波。相比选取较大数据窗口的传统多次波自适应相减方法,本文方法减少了大约48%的计算时间。

表2 实际数据的运行时间

5 结论

与传统的基于单窗口匹配的多次波自适应相减方法相比,采用多窗口联合优化的方法进行多次波自适应相减可以更有效地压制残余多次波并保护一次波,且计算效率与基于小窗口匹配的传统多次波自适应相减方法相当。但在实际应用中,多窗口联合优化方法中的窗口匹配个数需要根据不同的地震资料进行选取。因此,在提高一次波与多次波分离精度的基础上实现智能化的多次波自适应相减是必要的。在未来的工作中,利用深度学习实现多次波自适应相减是我们后续的重要研究方向。