不同维度下层间多次波正演模拟及其应用

黄建东,胡天跃,谢 飞,肖彦君,魏哲枫,朱成宏,刘 韬

(1.北京大学地球与空间科学学院,北京100871;2.中国石油化工股份有限公司石油勘探开发研究院,北京100083)

目前,中国西部地区已经成为油气勘探的重点地区之一,但是在该地区油气勘探深度内普遍存在低速夹层,例如四川盆地二叠系和奥陶系的低速泥页岩层、塔里木盆地侏罗系煤层等。一系列高低速地层组合产生大的波阻抗差异,地震波信号在这些波阻抗差异大的界面之间来回反射,使得层间多次波发育。由于上覆地层生成的层间多次波会掩盖下伏地层的一次反射波信号,因而不利于地震数据准确成像,会产生虚假构造,影响解释的精度[1]。层间多次波压制是陆上地震勘探资料处理最困难的环节之一。目前对层间多次波的生成机制和响应特征还不是很清楚,因此利用数值模拟方法研究层间多次波非常必要。

地震波场数值模拟方法主要分为两大类,一类以射线理论为基础,另一类以波动方程为基础。其中以波动方程为基础的地震波正演模拟方法应用最为广泛,包括有限差分法[2-3]、有限元法[4-5]、谱元法[6]和间断有限元方法[7-8]等。尽管这些数值模拟方法具有很大的优势,如有限差分法计算效率高,占用内存小;有限元类方法对地形描述更准确,计算精度高,但它们模拟的是总地震波场信号,无法将一次波和层间多次波信号单独分离,缺乏灵活性,对研究层间多次波的响应机理极其不方便。在实际应用中,研究人员利用预测方式压制多次波,如扩展的自由表面多次波压制(SRME)方法[9-10]、拉东变换方法[11]、虚同相轴方法[12-13]等,而不是直接研究多次波的生成机理特征。当前大多数学者对多次波的研究也主要集中在表面多次波,如LIU等[14]提出最小二乘表面多次波偏移方法,叶月明等[15]提出分阶表面多次波偏移成像,李强等[16]提出分阶表面多次波数值模拟方法,石颖等[17]基于波动理论预测三维表面多次波等。对层间多次波的讨论深度和广度却明显不如表面多次波。主要原因在于层间多次波的产生机理更加复杂,其研究难度也比表面多次波更大。

层间多次波模拟方法可以将一次波和层间多次波直接分离,且模拟波场的相位和振幅与地质属性保持一致。KENNETT[18]最早提出基于反射率法的层间多次波模拟方法,但该方法目前无法很好地适应介质的横向变化;COVEY等[19]提出一种基于射线追踪的层间多次波模拟方法,该方法运算效率较高,能处理简单介质中的层间多次波模拟问题,但无法应对复杂变化的模型;BERKHOUT[20]提出一种基于波场延拓的全波场模拟方法,弥补了有限差分等只能一次性模拟总波场的缺陷,可以分阶次模拟波场,且能够处理相对复杂的地质模型;匡伟康等[21]提出自适应可控层的层间多次波模拟与识别技术,进一步提高了效率,同时可忽略其它层位的影响,可以针对特定层的层间多次波进行模拟;戴晓峰等[22]提出叠前反射率正演模拟层间多次波方法,对川中地区的层间多次波进行了有效识别。

在上述研究的基础上,我们进一步提出了一种层间多次波模拟方法,即分别在不同维度下分阶模拟层间多次波,并采用傅里叶有限差分方法作为波场延拓算子,提高地震波的横向传播精度。多次波分阶的过程完全可控,一次循环得到一次反射波,二次循环得到一次反射波和一阶层间多次波。通过设置对应的迭代次数,可得到对应阶次的层间多次波。循环次数越高,波场信息越丰富。本文研究了层间多次波在一维、二维和三维模型中的传播规律,并对比分析了叠前和叠后层间多次波地震数据与全波场数据的关系。

1 基本原理

层间多次波数值模拟方法可单独将不同阶次的层间多次波分离出来,主要包含两个过程:一个是层间多次波分阶过程,满足反射和透射条件;另一个是地震波传播过程,基于波场延拓算子传播地震波。

1.1 层间多次波分阶模拟

全波场模拟(FWMod)方法最早由BERKHOUT[20]提出,该方法将地震数据看成是一种全波场数据,由一次反射波和各阶层间多次波叠加而成(本文主要研究层间多次波,假设已经消除了表面多次波的影响)。下面具体描述波场分阶模拟的基本原理。

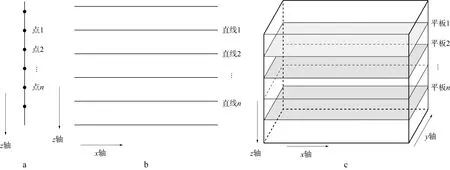
图1 一维(a)、二维(b)和三维(c)模型分解示意

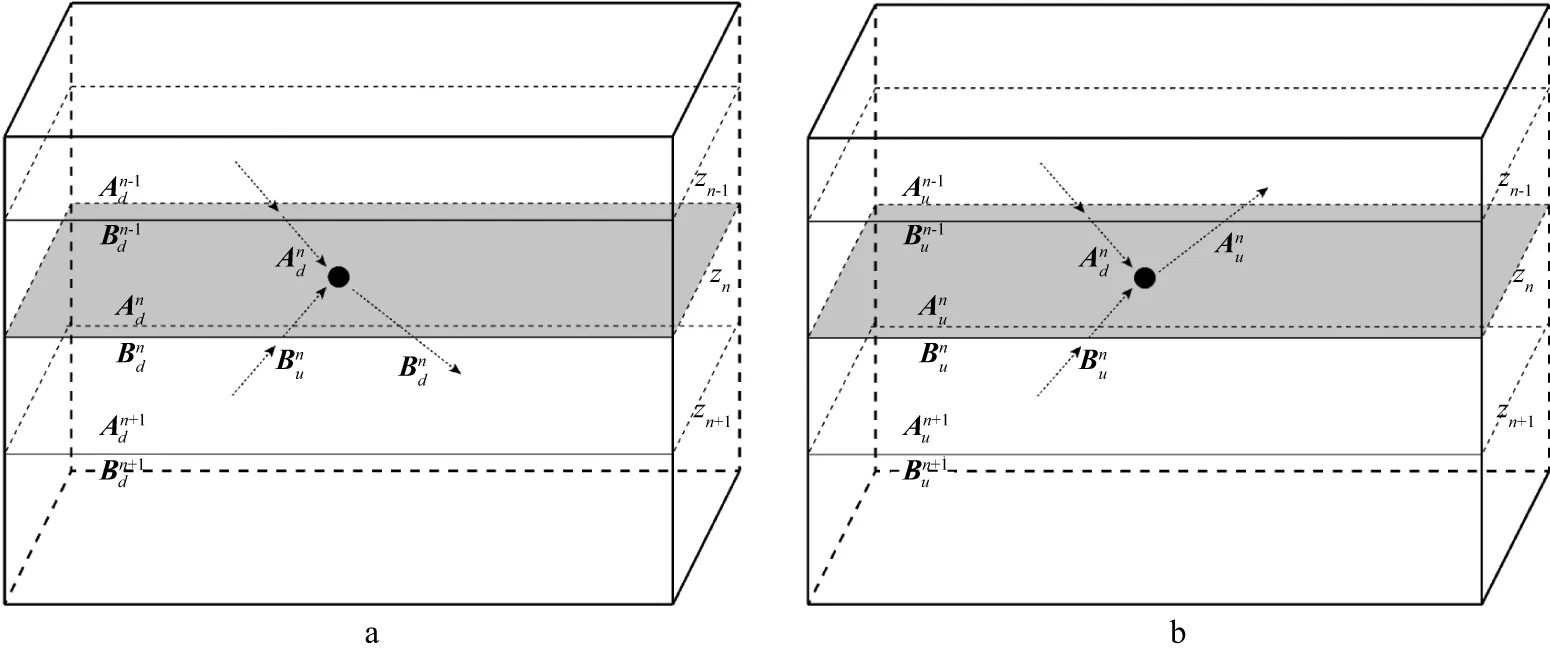
图2 波场延拓过程中的波场关系a 下行延拓;b 上行延拓

(1)

(2)

(3)

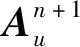
(4)

单程波数值模拟以递归的方式完成波场传播。当波场传播至某一层界面时,均要满足方程(1)至方程(4)的关系式,如地震波从界面zm传播至界面zn时,可以得到关于界面zn的下行波和上行波表达式分别为:

(5)

(6)

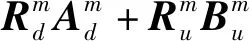
(7)

(8)

公式(7)和公式(8)给出了透射矩阵与反射矩阵之间的关系,I表示单位对角矩阵。根据公式(5)和公式(6),波场在不同的界面之间不断地传播和散射,在地表被观测系统接收,形成地震记录。

公式(5)和公式(6)仅仅表示在一次循环过程中的上行波场和下行波场计算。地震波场的分阶模拟是一个不断循环迭代的过程,可通过控制其循环次数来获得对应阶次的波场。在本文中,一次反射波被认为是0阶层间多次波。层间多次波模拟循环过程如图3所示,通过第一次循环,模拟得到0阶层间多次波场(图3a),图中的圆点表示延拓过程中激发的二次源。每增加一次循环可获得更高一阶的层间多次波。一阶层间多次波的生成机制如图3b中的绿色路径所示,二阶层间多次波的生成机制如图3c所示(蓝色路线)。若要模拟更高阶次的层间多次波,则需要更多的循环迭代过程。

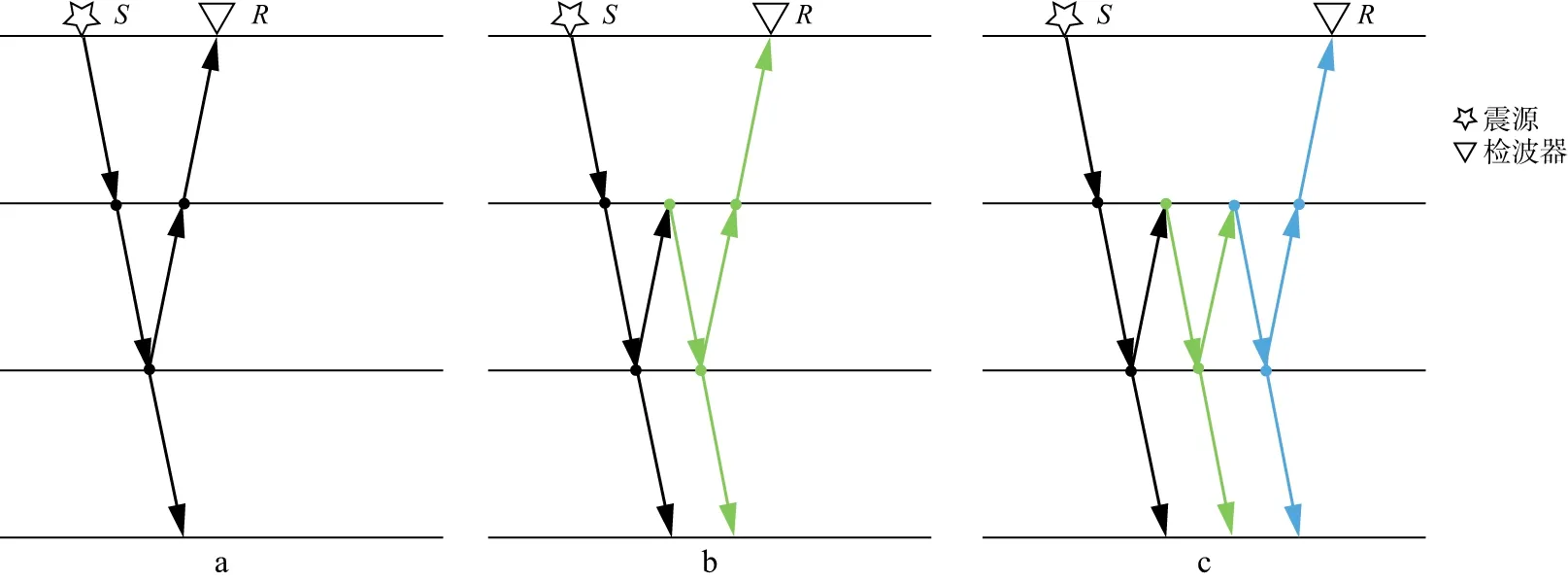
图3 层间多次波模拟循环示意a 0阶层间多次波循环;b 一阶层间多次波循环;c 二阶层间多次波循环

上面对三维情况下层间多次波的生成机理和特征作了详细介绍,据此可实现层间多次波的分阶数值计算。对于一维和二维模型中的层间多次波模拟也可以按照类似的思路进行数值计算。进行层间多次波分阶模拟时,波场延拓算子要保持好的稳定性,其在深度域满足递推关系(图4),波场延拓算子表达式为:

图4 延拓算子递推示意a 向下递推;b 向上递推

(9)

(10)

公式(9)和公式(10)表明波场延拓算子的累乘传递性质。

1.2 傅里叶有限差分波场延拓算子

波场延拓算子的精度会影响数值模拟的精度,因而其备受关注。本文选取傅里叶有限差分方法作为波场延拓算子,该方法可以利用有限差分校正项提高地震波在横向上的传播精度。横向非均匀介质中的三维频率域单程波方程表达式为[23]:

(11)

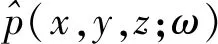
(12)

(13)

(14)

方程(12)表示相移算子;方程(13)表示慢度修正项,其中Δl表示慢度,其值为Δl=1/v-1/v0;方程(14)是横向上强速度差异的修正项,a和b为常系数。实际上,方程(12)、方程(13)和方程(14)可以等效为:

(15)

方程(15)是傅里叶有限差分延拓算子。利用波场延拓算子和迭代循环,可以实现高精度层间多次波的分阶数值模拟。

2 数值实例

利用层间多次波模拟技术在不同维度的模型中进行数值模拟,从而识别单炮记录中的层间多次波和一次反射波,并对叠前和叠后的地震数据进行分析。

2.1 一维模型

首先,构建一个一维模型(图5a),该模型含有4个强波阻抗差异反射界面,2个速度反转区。模型密度为常数2.0g/cm3。由于存在强速度差异,导致层间多次波发育,且多次波振幅能量较强。使用主频30Hz的雷克子波作为激发震源,时间采样间隔为5ms,记录时间为3.5s。图5b展示了总的波场信号,图5c至图5f是0～3阶层间多次波信号。从模拟的结果中可以得到4个一次反射波以及各阶层间多次波,一阶层间多次波的幅值量级与一次反射波大致相当,而二阶和三阶层间多次波幅值与一次反射波相差大约102倍。四阶以上的多次波相对于一次反射波幅值能量很弱。从走时来看,一次反射波与多次波相互混杂,低阶多次波与高阶多次波也相互混杂,它们之间都没有明显的时间分界线。

图5 一维模型层间多次波模拟a 一维速度模型;b 总的波场信号;c 0阶层间多次波;d 一阶层间多次波;e 二阶层间多次波;f 三阶层间多次波

2.2 二维模型

选取中国西北某地区的测井曲线进行二维建模,模拟分析该地区的层间多次波特征。图6为测井曲线和据此设计的速度模型。其中图6a中蓝色曲线为实际的声波测井曲线,黑色曲线为根据实际测井曲线构建的近似层状速度模型,图6b为根据图6a中黑色曲线构造的二维层状模型,模型大小为7.5km×12.5km。使用雷克子波作为激发震源。模拟数据道间距为0.02km,最大偏移距为6.25km,采用中间放炮两边接收的观测系统。本文方法模拟的炮集数据如图7所示,其中图7a是模拟的总波场,图7b是分离的一次反射波,图7c是分离的一阶层间多次波。从图7可以看到实现了一次反射波和一阶层间多次波的有效分离。同时为了研究层间多次波对地震数据处理的影响,对模拟的地震资料利用Geoeast软件进行速度分析,拾取的速度谱如图8所示,其中图8a是一次反射波速度谱,图8b是总波场速度谱。对比图8a和图8b可知,增加层间多次波后,速度谱中产生了很多靠近一次反射波能量团的层间多次波能量团,这些层间多次波能量团会影响一次波能量团的拾取,从而影响最终的速度谱拾取精度。并且层间多次波的叠加速度小于一次反射波。这种现象在实际地震资料处理中经常出现。

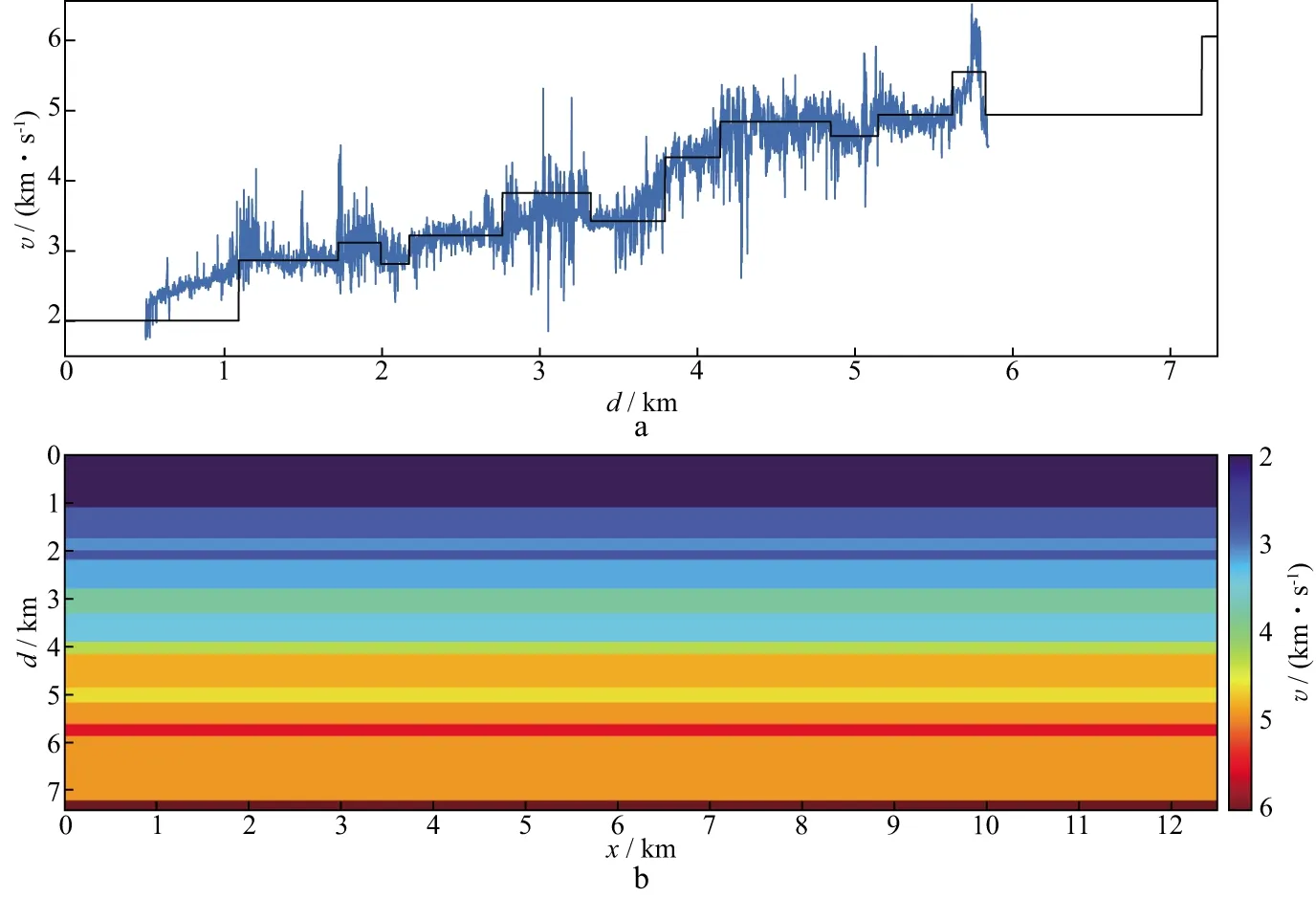
图6 测井曲线(a)和二维层状速度模型(b)

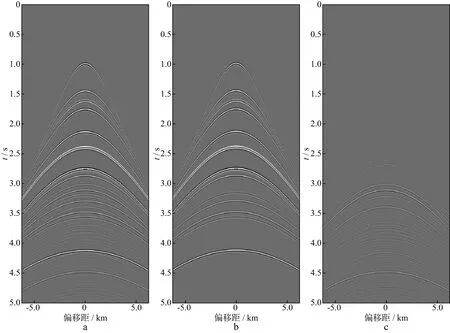
图7 模拟的炮集数据a 总波场;b 分离的一次反射波;c 分离的一阶层间多次波

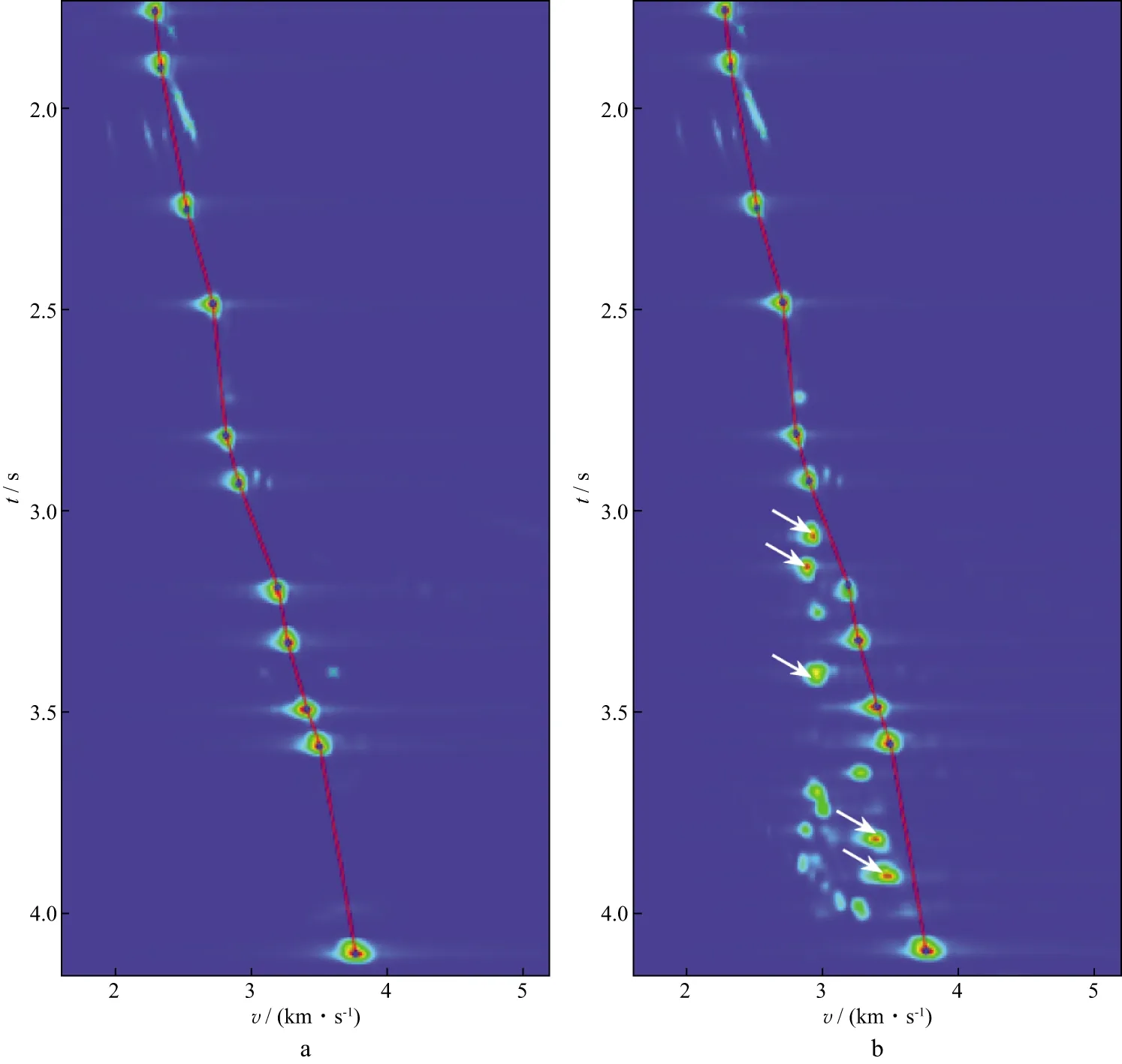
图8 模拟数据的速度谱a 一次反射波速度谱;b 总波场速度谱

为了进一步研究叠后地震数据之间的关系,构建了一个弱横向非均匀介质的地堑模型,模型的水平长度为9.6km,深度为4.0km。在深度为1.8km处有一个凹陷构造,具体的速度结构如图9所示。假设介质密度为常数2.0g/cm3。记录时间长度为3.5s,时间采样间隔为5ms,模拟数据的炮间距为0.02km,最大偏移距4.3km,总共模拟481炮。本文对不同的数据体进行了叠加处理,获得相应的零偏移距剖面,如图10所示,其中图10a是基于有限差分法得到的叠加剖面,图10b至图10d依次是0阶到二阶层间多次波叠加剖面。黑色箭头指的是与有限差分数据对应的一次反射波叠加结构,橙色箭头表示与有限差分数据对应的一阶层间多次波叠加结构,红色箭头表示对应的二阶层间多次波叠加结构。经过对比可发现不同阶次层间多次波的叠加剖面构造与有限差分计算的剖面构造相对应,证明了单程波数值模拟层间多次波的正确性,同时说明观测的地震记录是不同阶次的层间多次波和一次反射波的组合。

图9 地堑模型速度结构

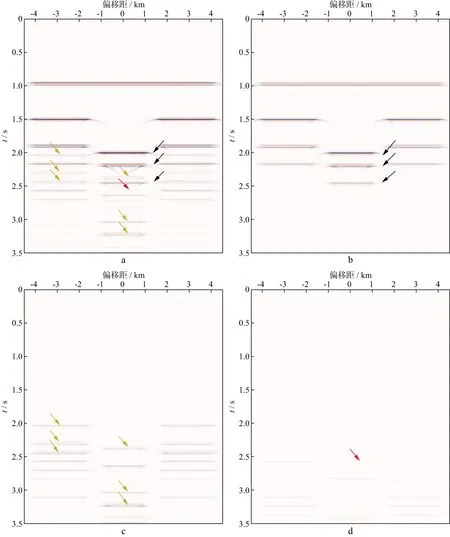
图10 零偏移距叠加剖面对比a 有限差分叠加剖面;b 0阶层间多次波叠加剖面;c 一阶层间多次波叠加剖面;d 二阶层间多次波叠加剖面

两个数值模拟结果表明不管在叠前还是叠后,地震数据可以理解为不同阶次层间多次波(一次反射波被认为是0阶层间多次波)的叠加。利用本文层间多次波数值模拟方法,联合测井资料,可辅助实际地震数据层间多次波的识别,指导其速度谱分析,帮助拾取一次反射波能量团。利用本文方法还可以确定层间多次波的聚集区域,便于指导后续的层间多次波的压制。

2.3 三维逆掩冲断层模型

利用本文方法对三维复杂模型进行层间多次波数值模拟。逆掩冲断层模型是公认的复杂模型,其含有断层、背斜、逆掩冲断层等复杂构造,横向非均匀性强。图11是逆掩冲断层模型的反射率模型,模型的大小为101×401×401个网格点。在模型的上表面(2km,2km)位置设置一个20Hz的雷克子波震源。

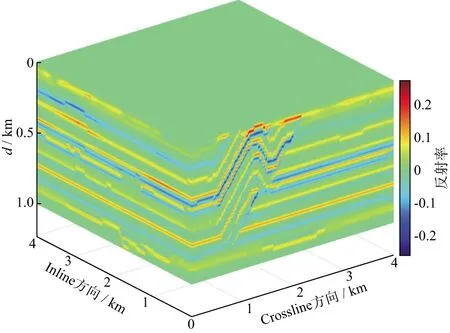
图11 逆掩冲断层模型的反射率

模型的网格尺度为10m,采样间隔为2ms,记录时长为2s。图12是过震源点沿Crossline方向合成的单炮记录,其中图12a是一次反射波单炮记录,图12b 和图12c分别是含有一阶和二阶层间多次波的单炮记录。从模拟结果中可以看出本文方法有效分离了三维复杂构造模型中产生的层间多次波。对比有限差分方法和本文层间多次波模拟方法对地震记录的近偏移距道集与远偏移距道集的计算结果(图13),可以看出两种方法对近偏移距道集的地震记录计算结果较好,但对远偏移距道集的计算结果有一定的差别。这是由于不同方法具有不同的属性导致。

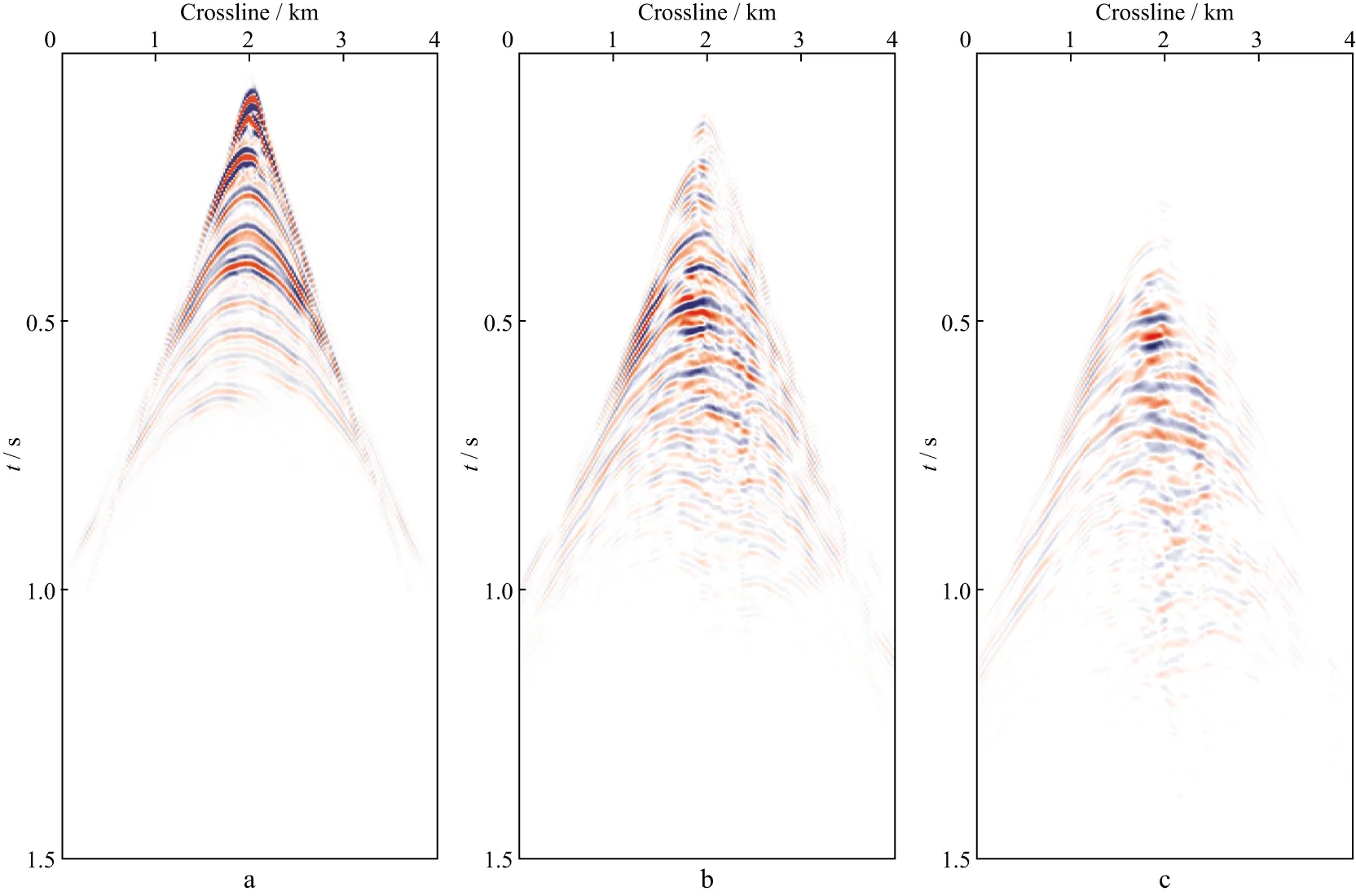
图12 含有不同阶次层间多次波合成单炮记录a 一次反射波;b 一阶层间多次波;c 二阶层间多次波

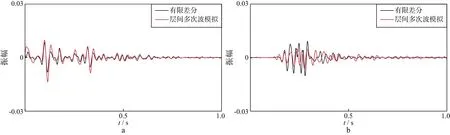
图13 有限差分方法和本文层间多次波模拟方法模拟的地震记录对比a 近偏移距;b 远偏移距

3 讨论与结论

本研究提出了一种层间多次波模拟方法,可在不同维度下对一次反射波和层间多次波进行有效分离,并使用傅里叶有限差分方法作为波场延拓算子,提高了在二维和三维情况下地震波的横向传播精度。波场分阶数值模拟分为散射和传播过程,两个过程相分离使得波场分阶模拟具有很大的灵活性,且本文方法具有迭代性,循环次数越多,波场信息越丰富。数值实例验证了本文方法可以有效地分离不同阶的层间多次波,并且叠前和叠后合成数据表明地震资料是各阶层间多次波的叠加。数值模拟结果还表明,本文层间多次波分阶模拟方法可以辅助识别实际地震资料中的层间多次波,指导速度分析,便于后续层间多次波的压制处理,从而提高深部储层解释的准确度。