基于高度残缺信息的分布式语言信任网络群决策方法
2022-05-23曾守桢胡英杰
曾守桢, 胡英杰
(1. 宁波大学商学院, 浙江 宁波 315211; 2. 复旦大学管理学院, 上海 200433)
0 引 言
近年来,社会网络背景下的群决策问题受到学者的广泛关注[1-4],如群体旅游路线评价、网商信用评价、风险投资项目评估等都是一个社会网络群决策问题。在社会网络群决策问题的研究中有两个主要问题不能忽视:① 评价与决策专家间的信任关系网络。由于群决策过程中专家涉及不同的专业领域,在知识、经验等方面都有其独特的特点,这意味着不同专家对决策结果有不同的影响,这种影响体现在专家权重的差异上[5],而专家间的信任关系作为专家权重的重要来源,其在群决策过程中的重要性不容忽视。相较于人为设定的专家权重,由信任关系网络获取的专家权重显得更加客观;② 专家评价信息的残缺(不完全)性问题。由于部分或所有专家对所涉及的问题缺乏深入的了解,经常会出现专家评价信息残缺或不完全的情况,其直接影响最终的决策结果,故专家评价信息的残缺性问题同样不能忽视。
关于专家间信任关系网络的研究,需关注以下两个方面。① 关于专家间信任关系的表征方式的研究,传统上主要以精确值(离散值与连续值)或二进制数表示为主[6-9]。其中文献[6]对Film Trust网站上的用户进行研究,其利用信任度为1~10的范围对电影进行信任度评估(1:最不值得信任;10:最值得信任)。文献[7]利用二元离散值(信任或不信任)表示用户间的信任关系。文献[8]利用区间[-1,1]的连续值来表示主体与推荐人之间的信任关系。文献[9]利用[0,1]间的实数来表示专家间的信任程度。然而,考虑到信任的主观性、模糊性和不确定性,人们往往更愿意用语言术语来表达信任程度,文献[10]则提出分布式语言信任函数来表征专家间的信任关系,并通过“高”、“中”、“低”3个等级来表达他们的信任,比传统的二元关系(信任或不信任)更加符合实际情况。② 关于信任传递算子的研究,研究者提出了包括T-norm、Uninorm (U)算子等众多信任传递算子[2-3,9,11-13]。如文献[2]基于Frank T-norm、T-conorm设计传递直觉模糊信任关系的信任传递算子。文献[9]基于T-norm设计传递实数的信任传递算子。文献[3]和文献[11]分别基于U算子和Einstein T-norm、T-conorm构造信任传递算子以传递专家间的信任函数关系。文献[12]基于代数T-norm设计了信任传递规则。文献[13]基于Archimedean T-norm 和T-conorm设计了区间值双重信任传递算子以传递区间值信任函数关系。上述研究都是以实数、直觉模糊数、信任函数等信任表征方式来设计信任传递算子,然而并没有基于分布式语言信任关系的信任传递算子的相关研究。此外,现有关于分布式语言信任社会矩阵的研究,没有对存在缺失的信任关系进行补全,且专家权重的获取方法都是基于Q量词,并未考虑社会矩阵中专家间的信任关系对专家权重的影响[14-15]。基于此,需提出一种能够传递分布式语言信任关系的传递算子来补全社会矩阵,进而基于信任社会矩阵确定专家权重。考虑到已有的信任传递算子并不适用于分布式语言信任环境,故本文提出一种新的基于代数T-norm的分布式语言信任传递算子来补全缺失的信任关系,并基于完整的分布式语言信任社会矩阵定义个体、群体信任中心度的概念以确定专家权重。
针对专家评价信息的残缺性问题,国内外已有众多学者对残缺信息的评估和补全方法进行了分析。文献[4]通过改进的 PageRank 算法和专家信任网络确定专家重要度,进而基于专家的重要度填充不完全的犹豫模糊评价信息。文献[12]利用二元语义表示专家的评价信息,并基于专家间的相对信任得分评估不完全二元语义决策矩阵中未知的二元语义值。文献[16]利用相对信任度和余弦相似度来评估不完全的基于精确数的评价信息。文献[17]提出一种基于相似度和贴近度的集聚度,并基于集聚度补全不完全偏好关系。文献[18-19]则分别基于信任得分和期望信任度提出专家间的相对信任度,并基于相对信任度评估专家的残缺评价信息。文献[20]提出了一种基于乘法一致性的不完全犹豫模糊偏好关系的归一化和缺失元素的估计方法。文献[21]通过其他类似专家的偏好来估计具有高度残缺(即一些专家可能无法提供关于替代方案的任何单一判断)的偏好信息。
目前,对于残缺偏好信息的研究成果比较多[4,12,20-22],但是基于高度残缺信息的多属性决策方法还不多见。高度或极端残缺信息在偏好关系环境下是指方案间的偏好关系存在某一行和某一列都未知的情形[21],而在多属性群决策问题中高度残缺信息可看成是某一方案下关于所有属性的评价信息都未知的情形。同时关于残缺值评估方法,上述大多数文献都是基于其他所有专家的现有评价意见来对残缺值进行评估和补全[4,12,16-19],这可能会导致某些专家的评价意见并不能被存在残缺信息的专家所接受。而且,根据意见动力学理论,人们更倾向于接受来自相似同伴的意见[23]。因此,在高度残缺的分布式语言信任评价信息背景下,本文提出一种基于K-近邻算法的评估方法。首先找出与存在残缺评价信息的专家距离最近(最相似)的K个专家,然后基于这K个专家的信息对残缺值进行评估。K-近邻算法保证了残缺信息的评估依靠与其最相似的专家意见,而非所有专家。
除了上述两个需注意的问题之外,对方案排序方法的选择也不能忽视。本文将改进的逼近理想解排序(technique for order preference by similarity to an ideal solution,TOPSIS)法引入分布式语言信任决策环境中,提出一种改进的基于分布式语言信任函数距离测度的TOPSIS评价方法,能够一定程度上降低仅由单个集成算子决策时造成的信息失真。
综上所述,针对现有研究存在的缺陷,本文提出一种基于高度残缺信息的分布式语言信任网络群决策方法。具体而言,首先提出一种分布式语言信任传递模型,进而补全残缺的分布式语言信任社会矩阵。在此基础上,利用分布式语言信任社会矩阵定义个体信任中心度和群体信任中心度,并通过它们的距离测度获取专家权重。其次,在专家评价信息高度残缺的情况下,根据K-近邻算法评估和补全专家的残缺评价信息。最后,利用分布式语言信任加权平均算子融合各决策矩阵,并基于改进的TOPSIS评价方法对方案进行排序。
1 预备知识
本节主要介绍分布式语言信任函数的一些基本概念以及分布式语言信任网络。
1.1 分布式语言信任函数
定义 1[10]设D={Dα|α=1,2,…,ξ}为一个语言术语集,则分布式语言信任函数T定义如下:
T={(Dα,φα)|α=1,2,…,ξ}
(1)

其中对于任意两个分布式语言信任函数T1和T2,其运算法则表示如下(η,η1,η2>0):
(2)ηT={(Dα,ηφα)|α=1,2,…,ξ};
(3) (η1+η2)T=η1T⊕η2T;
(4)T1⊕T2=T2⊕T1;
(5)η(T1⊕T2)=ηT1⊕ηT2。
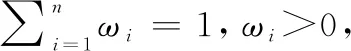
(2)
为了比较分布式语言信任函数的大小,文献[10]定义了分布式语言信任函数的期望度E和不确定性度U如下:
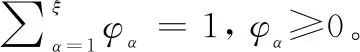
(3)
(4)
式中:E(T)越大,函数T的分值度就越大;U(T)越大,函数T的分值度就越小。
1.2 分布式语言信任网络
群决策过程中专家间的信任网络是由专家节点和专家节点间的有向边(即信任关系)组成。而分布式语言信任网络则是指用分布式语言来表示专家间的信任关系,进而构成分布式语言信任网络,如图1所示。其中有向箭头表示专家间的分布式语言信任关系,如专家e1对专家e5是一种直接的信任关系。从图中可以看出,专家e1对专家e2的信任关系未知,没有直接相连的有向箭头,是一种间接的信任关系,可通过中间专家节点(如e3和e5)的传递得到专家e1对专家e2的间接信任。
1.3 T-norm与代数T-norm
T-norm是决策过程中信息聚合的重要工具,目前也被广泛应用于构造社会网络决策过程中的信任传递算子,定义如下:
定义 4[24]二元函数N:[0,1]2→[0,1]被称为T-norm当且仅当满足
(1) 交换性
∀x,y∈[0,1],N(x,y)=N(y,x)
(2) 结合性
∀x,y,z∈[0,1],N(N(x,y),z)=N(x,N(y,z))
(3) 单调性
若x≤x1,y≤y1,则N(x,y)≤N(x1,y1)
(4) 单位元
∀x∈[0,1],N(1,x)=x
代数T-norm(表示为A⊗)也是一个T-norm,其数学表达式为
A⊗(x,y)=x⊗y=xy
(5)
由于T-norm具有结合性,故代数T-norm也具有结合性,即
(6)
代数T-norm的一个重要性质为:T-norm小于等于最小算子min,数学表达式为
A⊗(x1,x2,…,xn)≤min {x1,x2,…,xn}
(7)
上述性质保证了由代数T-norm构造的信任传递算子在传递过程中信任值是递减的。
因此考虑到代数T-norm的结合性、小于等于最小算子min等特性,下节将提出一种基于代数 T-norm的分布式语言信任环境下信任传递模型。
2 基于分布式语言信任函数的信任传递模型
目前分布式语言信任社会矩阵大多都是不完整的[10,14-15],且基于此类不完整的分布式语言信任社会矩阵所求得的专家权重是不精确的,这将影响最终的决策结果。本文通过定义分布式语言信任传递和聚合算子,将不完整的分布式语言信任网络补全。
2.1 基于分布式语言信任函数的信任传递算子
定义 5设是分布式语言信任函数的集合。分布式语言信任传递算子PA,PA:×→,其中T1表示专家e1对专家e2的直接信任关系,T2表示专家e2对专家e3的直接信任关系,则专家e1对专家e3的信任关系T3可表示为
(8)
其中,
下面对信任传递算子PA的特殊情形作简要分析。
(1) 当专家e1完全信任专家e2且专家e2完全信任专家e3时,可得专家e1完全信任专家e3。
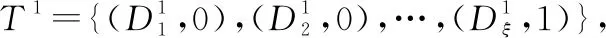
{(D1,0),(D2,0),…,(Dξ,1)}
即专家e1完全信任专家e3。
(2) 分以下两种情况讨论:①当专家e1完全信任专家e2且专家e2完全不信任专家e3时,可得专家e1完全不信任专家e3;②当专家e1完全不信任专家e2且专家e2完全信任专家e3时,可得专家e1完全不信任专家e3。
下面证明情况①,其中情况②的证明与情况①类似。
由①可知,
故专家e1对专家e3的信任关系为
{(D1,1),(D2,0),…,(Dξ,0)}
即专家e1完全不信任专家e3。
(3) 当专家e1完全不信任专家e2且专家e2对专家e3的信任关系未知时,可得专家e1完全不信任专家e3。即
{(D1,1),(D2,0),…,(Dξ,0)}
即专家e1完全不信任专家e3。
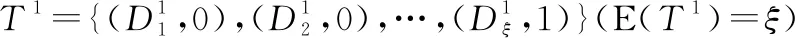
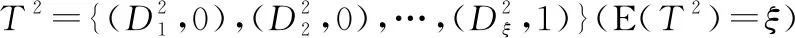
因此,专家e1对专家e3的信任关系可表示成如下形式:
T3=PA(T1,T2)=
(9)
由于在路径传递的过程中可能会出现专家个数大于3,即中间的专家节点数大于2的情形,因此需要对传递路径上中间的专家节点数大于2的情形进行讨论以得出最终的信任关系。
当中间的专家节点数n=3时,有
--------------------
--------------------
其中,代数T-norm (A⊗)具有结合性,即
且有
则当n≥3可得:
(10)
(1) 当n=3时等式成立,已证。
(2) 假设当n=k时等式成立,则当n=k+1时,有
Tk+2=PA(T1,T2,…,Tk,Tk+1)=PA(PA(T1,T2,…,Tk),Tk+1)=
其中
基于式(6)和式(10),可得
Tn+1=PA(T1,T2,…,Tn)=PA(PA(T1,T2,…,Tn-1),Tn)=
(11)
2.2 基于分布式语言信任函数的信任聚合算子
考虑到信任传递过程中存在多条传递路径的情况,本文提出一种基于路径长度的诱导有序加权平均(induced ordered weighted averaging operator based on path length,L-IOWA)算子来聚合多条路径的信任信息,以保证每条路径的信任信息得到充分利用。首先定义在多条路径情形下路径Pi优于路径Pj的情况。
定义 6设L表示路径的长度,E表示分布式语言信任函数的期望,则路径Pi优于路径Pj的定义如下:
(1)L(i) (2)L(i)=L(j)∧E(Ti)>E(Tj)⟹PifPj。 基于路径间的优先排序以及路径权重,我们提出一种基于路径长度的诱导有序加权平均算子以融合多路径的信任信息,定义如下。 (12) 在得到完整的分布式语言信任网络后,本文提出一种基于个体信任中心度和群体信任中心度的专家权重求解方法,定义如下。 定义 8设Ths表示分布式语言信任网络中专家eh对专家es的信任关系,则个体信任中心度(individual trust centrality,ITC)和群体信任中心度(group trust centrality,GTC)分别为 (13) (14) 故专家es权重定义为 (15) (16) 该距离测度满足以下性质: (1) 0≤d(T1,T2)≤1; (2)d(T1,T2)=0当且仅当T1=T2; (3)d(T1,T2)=d(T2,T1); (4)d(T1,T3)≤d(T1,T2)+d(T2,T3)。 在现实的群决策过程中经常会存在这样的情况,即部分专家对所涉及的问题缺乏深入的了解,导致专家提供的评价信息存在残缺的情形。目前对于偏好信息残缺或不完全问题的研究成果比较多[4,12,17,20-22],但基于高度残缺信息的多属性决策方法还不多见。同时,关于残缺信息评估方法,很多文献都是基于其他所有专家的评价意见来评估残缺值[4,12,16-19],忽略了存在残缺评价信息的专家对其他专家评价意见的接受意愿,而且人们更倾向于接受来自相似同伴的意见[23]。基于此,本文研究在分布式语言信任决策环境下评价信息存在高度残缺的情形,并利用K-近邻算法评估专家的高度残缺评价信息以保证评估值能被存在残缺评价信息的专家所接受,即通过找出与决策矩阵中具有高度残缺评价信息的专家距离最近的K个专家,即K个与具有高度残缺评价信息的专家最相似且属于同一类别的专家,并基于这K个专家评估残缺的评价信息。具体过程如下: (1) 计算其他专家与存在高度残缺评价信息专家的距离; (2) 通过距离测度,确定K个距离最近的专家; (3) 利用式(2)评估残缺的评价信息。 其中第一步中的距离测度通过以下公式进行计算。即假设有l个专家es(s=1,2,…,l),相应的决策矩阵为As(s=1,2,…,l),有m个备选方案Xi(i=1,2,…,m),n个评价属性Cj(j=1,2,…n)。设Ah为具有高度残缺评价信息的专家决策矩阵,则Ah与As之间的距离测度定义为 (17) 在补全分布式语言信任决策矩阵后,根据式(2)将各个分布式语言信任决策矩阵整合成分布式语言信任群决策矩阵,表示为 此时,可计算分布式语言信任正、负理想解,用X+表示分布式语言信任正理想解,X-表示分布式语言信任负理想解: (18) (19) 根据式(18)和式(19)以及定义9的距离测度公式可计算每个方案Xi与分布式语言信任正理想解X+、负理想解X-之间的距离,即 (20) (21) 其中,d(Xi,X+)越小,表明方案Xi越好;d(Xi,X-)越大,表明方案Xi越好。 因此,可计算每个方案Xi的改进贴近度(improved closeness degree,ICD)为 (22) 进而基于ICD(Xi)对方案进行排序。 综上,基于高度残缺信息的分布式语言信任网络群决策方法的具体步骤如下。 步骤 1基于分布式语言信任传递算子式(11)和聚合算子式(12)将分布式语言信任社会矩阵补全。 步骤 2基于式(16),计算个体信任中心度和群体信任中心度的距离测度,进而获取专家权重。 步骤 3基于K-近邻算法获取与存在高度残缺信息的专家距离最近的K个专家,并通过专家权重和式(2)将残缺信息补全。 步骤 4计算群决策矩阵A,并利用式(18)~式(21)计算每个方案Xi与分布式语言信任正理想解X+和负理想解X-之间的距离。 步骤 5基于式(22),计算每个方案Xi的贴近度ICD(Xi),并根据其大小对方案进行排序。 相应地,该群决策方法的流程如图2所示。 综上分析,该群决策方法的特点及创新点主要体现在以下几个方面。 (1) 设计了传递分布式语言信任关系的信任传递模型,并基于信任关系定义个体信任中心度ITC和群体信任中心度GTC,进而获取专家权重,克服了已有文献关于分布式语言信任社会矩阵的研究中存在缺失信任关系的缺陷,同时弥补了专家权重获取时未考虑专家间信任关系的不足。 (2) 基于高度残缺信息的决策问题,提出了在高度残缺分布式语言评价信息环境下的K-近邻算法,相较于基于其余专家的评价信息对残缺值进行评估的方法,利用相似专家的评价意见评估残缺值,更能反映存在残缺信息的专家对评价意见的接受意愿,即并非所有专家的评价意见都能被接受。 (3) 将改进的TOPSIS引入分布式语言环境中,并结合DTWA算子对方案择优,可有效避免由单个DTWA算子对方案择优所带来的信息失真问题。 假设有3个外卖平台{X1,X2,X3},相应的属性为餐品的安全性、外卖的配送快慢程度、餐品下单的优惠力度、餐品的美味程度,即属性集{C1,C2,C3,C4},属性权重分别为w=[0.35,0.3,0.15,0.2]T。现需为大学新生推荐一款性价比最高的外卖平台,故咨询五位在校大学生{e1,e2,e3,e4,e5},利用式(1)中分布式语言信任函数T,并综合上述4个属性对3个外卖平台进行评价,以选出性价比最高的外卖平台。其中,假定式(1)中ξ=3,且令D1=“低”,D2=“中等”,D3=“高”。此外,上述5位大学生可构成如下的分布式语言信任社会矩阵: -------------------- -------------------- 式中:“-”表示专家间不存在直接信任关系;“×”表示专家对自我的信任不予考虑。 步骤 1根据信任传递算子式(11)和信任聚合算子式(12),将分布式语言信任社会矩阵补全。以专家e1对专家e4的信任关系为例,专家e1到专家e4有3条信任传递路径,分别为L1:e1→e2→e4、L2:e1→e5→e3→e4和L3:e1→e5→e3→e2→e4,根据式(11)可得 上述3条传递路径的权重可由Q量词计算,令a=0.5,可得w1=0.58,w2=0.24,w3=0.18。故专家e1对专家e4的信任关系为 其他专家间的信任关系可类似计算,故可得如下完整的分布式语言信任社会矩阵: -------------------- 步骤 2根据式(13)和式(14),可得决策专家的信任中心度和群体信任中心度: ITC(e1)={(D1,0.652 5),(D2,0.115 0),(D3,0.232 5)} ITC(e5)={(D1,0.357),(D2,0.140),(D3,0.503)} 进而根据式(15),得到专家权重为 ω1=0.197 步骤 3根据K-近邻算法计算与专家e1距离最近的K个专家,并利用K个专家的权重评估专家e1的残缺值。其中5位专家的分布式语言信任评估矩阵分别如表1~表5所示。 表1 专家e1的分布式语言信任评估矩阵 表2 专家e2的分布式语言信任评估矩阵 表3 专家e3的分布式语言信任评估矩阵 表4 专家e4的分布式语言信任评估矩阵 表5 专家e5的分布式语言信任评估矩阵 通过式(17)计算专家e1与其余专家的距离测度,可得 d(e1,e2)=0.356 取K=3,则根据上述距离测度可得,与专家e1距离最近的3个专家分别为专家e3,e4,e5,故专家e1的残缺值可评估为 (23) 其中,ρ1,ρ2,ρ3为专家e3,e4,e5的权重标准化后的值,即ρ1=0.333,ρ2=0.352,ρ3=0.315。进一步计算可得 步骤 4计算每个方案Xi与分布式语言信任正理想解X+和负理想解X-之间的距离d(Xi,X+)和d(Xi,X-)。首先根据式(2)计算群决策矩阵,结果如表6所示。 表6 基于分布式语言信任函数的群决策矩阵 根据表6可计算正负理想解X+和X-: X+={((D1,0.116),(D2,0.458),(D3,0.426)), ((D1,0.241),(D2,0.435),(D3,0.324)), ((D1,0.175),(D2,0.424),(D3,0.401)), ((D1,0.358),(D2,0.185),(D3,0.457))} X-={((D1,0.584),(D2,0.297),(D3,0.119)), ((D1,0.463),(D2,0.412),(D3,0.125)), ((D1,0.564 4),(D2,0.382 3),(D3,0.053 3)), ((D1,0.374),(D2,0.544),(D3,0.082))} 则可得 d(X1,X+)=0.020 步骤 5根据式(22)计算每个方案Xi的贴近度ICD(Xi),i=1,2,3: ICD(X1)=0 因此方案排序为:X1>X3>X2,即第一个外卖平台X1的综合性价比最高。 在上述决策过程中,对于信任聚合时路径权重的计算,需注意的是,其假定参数a=0.5。显然当参数a取不同值时,每条路径权重不同,相应地信任聚合结果也会不同,进而会对决策结果产生影响。因此,下面考虑参数a的变化对方案排序结果的影响,鉴于a=0时,路径权重计算会出现00,没有意义;a=1时,当两条路径长度不同时,路径权重都为0.5。事实上,路径越短权重应越大,路径越长权重应越小,故参数a=1也不可取。因此,本文以0.2为步长,在区间(0,1)内对参数a进行取值以分析最终的决策结果,即取a=0.1,0.3,0.5,0.7,0.9。具体的方案贴近度ICD以及排序结果如表7所示。 表7 参数a对方案排序的影响 相应地,方案的贴近度ICD与排序随参数a变化的趋势如图3和图4所示。 由图3可以看出,随着参数a的不断增大,方案X2与X3的贴近度ICD呈现递减的趋势,但波动幅度不大。而X1的ICD不变,始终保持在最大值0。图4中,考虑到a=0.1,0.3,0.5,0.7,0.9时方案排序始终保持一致,即X1>X3>X2,因此图4中只画出一条折线,由于最优方案都为X1,方案排序一致。因此,本文提出的方法是相对稳定的,同时也说明方案排序对参数a的选择并不敏感。 为体现本文方法的可行性与有效性,下面采用两种方法来计算实例,进而与本文方法(a=0.5)进行对比分析。 方法 1利用文献[10]中分布式语言信任关系的入度中心度的期望值来获取专家权重,并利用文献[19]中基于期望信任度的相对信任度评估残缺值,在此基础上,利用DTWA算子集成决策矩阵,并基于改进的TOPSIS聚合评价信息。 方法 2利用文献[14]中的Q量词获取专家权重,并利用文献[4]中残缺信息的评估方法评估残缺值,在此基础上,利用DTWA算子聚合决策矩阵,同时基于改进的TOPSIS聚合评价信息。 不同方法得到的ICD值如图5所示,其中ICD(Xi)表示方案Xi的贴近度,本文方法与方法1、方法2所得ICD(X1)的值均为0,故图5中不显示。 从图5可看出,本文方法与方法1、方法2所得ICD(X2)与ICD(X3)的值均不同,但3种方法所得到的排序结果均为ICD(X1)>ICD(X3)>ICD(X2),最优方案都为X1,说明本文所提出的方法是可行的。 为进一步体现本文方法的优越性,下面从专家权重的获取方法与残缺信息的评估方法两个角度进行分析,具体结果如表8所示。 表8 不同方法的对比分析 从表8可以看出,不同方法所得专家权重与残缺信息的评估也不同。具体而言: (1) 方法1中专家权重的获取虽基于专家间的信任关系,但并未将残缺的分布式语言信任社会矩阵补全,基于残缺的分布式语言信任关系得到的期望值并不准确,进而获取的专家权重也不准确。同时基于其余专家信任关系的期望的相对信任度评估残缺值并没有考虑到存在残缺评价信息的专家对其余专家评价信息的接受意愿。而本文方法不仅通过提出的信任传递模型将残缺的分布式语言信任社会矩阵补全,进而基于分布式语言信任关系的个体和群体信任中心度获取专家权重,结果更准确。而且通过提出的分布式语言K-近邻算法对残缺评价信息进行评估,一定程度上反映了存在残缺评价信息的专家对其余专家评价信息的接受意愿。 (2) 方法2中专家权重的获取基于量词Q,虽是以专家间信任关系的大小为诱导变量来获取权重,但信任关系本身并没有用于专家权重的求解,且分布式语言信任社会矩阵是残缺的,以残缺的信任关系作为诱导变量也存在问题。此外,基于其余专家的重要度来评估残缺的评价信息,同样没有考虑到存在残缺评价信息的专家对其余专家评价信息的接受意愿。而本文方法的提出恰好能克服上述两个缺陷。 本文提出一种基于高度残缺信息的分布式语言信任网络群决策方法,主要体现在以下几个方面:第一,针对残缺的分布式语言信任社会矩阵,结合代数T-norm的优良性质,提出一种分布式语言环境下基于代数T-norm的信任传递算子。并考虑到多条传递路径存在的情形,提出一种基于分布式语言的信任聚合算子。第二,针对目前分布式语言信任群决策问题在专家权重计算时并未利用专家间信任关系这一情形,定义了基于分布式语言信任关系的个体信任中心度和群体信任中心度,并通过它们的距离测度来获取专家权重。第三,针对专家评价信息高度残缺的情形,提出一种基于K-近邻算法的评估方法,通过确定与存在高度残缺评价信息的专家距离最近(最相似)的K个专家来评估残缺的评价信息,而非基于所有专家的评价意见进行评估,因为可能某些专家的评价意见并不能被存在高度残缺评价信息的专家所接受。值得注意的是,本文研究的群决策方法是以分布式语言为决策背景的,事实上还可将其拓展到其他非确定性数据环境中,如概率语言集[19]、犹豫模糊集[26]、直觉模糊集[2]等。同时,本文所提出的群决策方法未考虑共识交互模型对决策结果的影响[9,13,19],相关研究笔者在未来的工作中会继续跟进。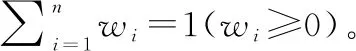

2.3 基于分布式语言信任网络的专家权重获取


2.4 高度残缺信息的评估(K-近邻算法)
3 基于高度残缺信息的分布式语言信任网络群决策方法
3.1 基于分布式语言信任函数的改进TOPSIS方法
3.2 基于高度残缺信息的分布式语言信任网络群决策方法
4 决策应用分析
4.1 实例分析
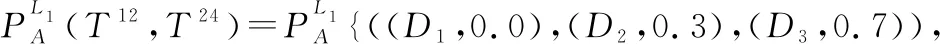

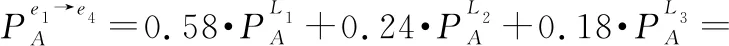
ITC(e2)={(D1,0.402),(D2,0.208),(D3,0.390)}
ITC(e3)={(D1,0.630),(D2,0.109),(D3,0.261)}
ITC(e4)={(D1,0.561),(D2,0.123),(D3,0.316)}
GTC(eg)={(D1,0.520 5),(D2,0.139 0),(D3,0.340 5)}
ω2=0.200
ω3=0.201
ω4=0.212
ω5=0.190




d(e1,e3)=0.218
d(e1,e4)=0.238
d(e1,e5)=0.258

d(X2,X+)=0.275
d(X3,X+)=0.164
d(X1,X-)=0.271
d(X2,X-)=0
d(X3,X-)=0.171
ICD(X2)=-13.54
ICD(X3)=-7.4414.2 参数敏感性分析

4.3 对比分析

5 结 论
