粗骨料嵌锁型混凝土的细观断裂机理研究

张雨,李犇,余盈,张琛

（佛山科学技术学院交通与土木建筑学院，佛山市智慧型陆地与海洋土木工程材料工程技术研究开发中心，广东佛山528225）

混凝土是含有砂浆和骨料的两相复合材料［1-3］，混凝土的行为取决于每个相的性质及其相互作用。常规混凝土的原材料由水泥、砂石和水组成，其中水泥砂浆占比很大，而混凝土中粗料含量通常控制在较低水平［4］。粗骨料是混凝土强度的框架，通常是混凝土材料中强度最高、耐久性最好以及体积稳定性最好的结构单元［5-6］。作为一种复合材料，只要骨料能够与水泥砂浆很好地结合，其性能就会随着骨料体积分数的增加而增加。随着混凝土掺量的增加和混凝土强度等级的提高，混凝土中水泥和胶凝材料的数量增加，导致大量混凝土在早期出现非常明显的裂缝，这影响了混凝土的服役性能，并已成为混凝土一种常见的“富贵病”［7-8］。

混凝土的力学性能是建筑结构设计的基础和混凝土结构的基本技术要求［9-11］。然而，力学性能并不是混凝土的绝对特征，它还受许多因素的影响。如在早期阶段，混凝土中大量的水泥和凝胶材料会引起显著的开裂现象，进而影响其后期的力学及耐久性能；粗骨料的体积含量相对较低，不仅不能充分发挥骨料强度对混凝土性能的提升作用，而且还会增加混凝土成本，造成资源浪费和环境负担增加等问题；混凝土的强度、优异的工作性能和耐久性能间的矛盾。目前，一些学者通过研究混凝土的骨胶比、粗骨料的最大粒径或体积掺量来构造高性能和高体积稳定的骨料嵌锁型混凝土，以期优化混凝土材料的综合性能及增大应用范围［12-14］。其中，作为一种新提出的粗骨料嵌锁型混凝土，现浇骨料混凝土是通过最大限度地提高材料性能和减少病害发生来改善混凝土使用寿命的新方法［15-17］。与传统混凝土相比，粗骨料有效嵌锁对混凝土的基本力学性能、耐久性能、经济性能及环保等方面都有积极的影响［18］。此外，一些学者通过对骨料嵌锁型混凝土的实验和工程应用进行了一些研究，但其力学机理，特别是断裂理论尚未得到系统的研究。断裂或开裂特性是混凝土最重要的工程和材料特性，是确保混凝土稳定性的必要标志。此外，骨料嵌锁型混凝土内部纳米结构和水化产物会受到粗骨料的影响从而进行重新分配。传统的力学模型在表征其断裂机理方面并不全面，需要建立多尺度模型进行理论分析。

在此背景下，研究骨料嵌锁型混凝土的断裂机理和理论计算模型。在细观力学与混凝土介观结构变化相结合的基础上，通过理论计算与数值分析，为骨料嵌锁型混凝土的力学机理提供理论补充和支持。

1 理论分析

基于能量、裂缝发展规律等因素，考虑粗骨料的增加和嵌锁对混凝土界面微观结构的影响，结合细观力学均匀化理论（RVE 模型），建立了骨料嵌锁型混凝土的断裂机理。

1.1 粗骨料嵌锁型混凝土的RVE 模型

假设细观尺度下混凝土基体中存在体积为V的弹性体，弹性体中粗骨料引起的夹杂和扰动中存在一个夹杂子域。基域和包含域具有不同的弹性张量和柔度张量。粗骨料相互作用产生的孔隙结构包裹体的不均匀性，会在均匀固体中产生应力场和应变场扰动。因此，含有孔隙结构夹杂物的弹性固体的应力应变方程可以表示为：

σ(X，x)=σ0(X)+σd(x) （1）

ε(X，x)=ε0(X)+εd(x) （2）

式（1）和式（2）中，σ(X，x)为含孔隙结构夹杂物水泥基弹性体的应力，ε(X，x)为含孔隙结构夹杂物水泥基弹性体的应变，σ0(X)为水泥基弹性体的应力，ε0(X)为水泥基弹性体的应变，σd(x)为非均质孔隙结构的扰动应力，εd(x)为非均质孔隙结构的扰动应变。

通过特征应变场与实际应变场的叠加，得到等效均匀固体应力场与原始非均匀应力场的关系。

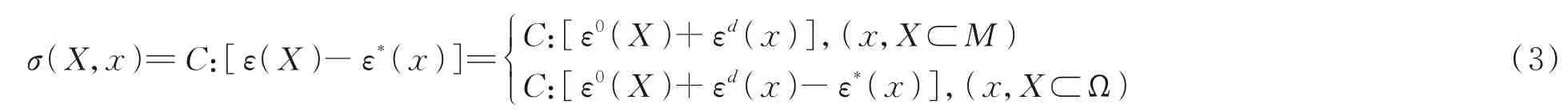
式（3）中C是非均匀固体的弹性张量，ε*(x)是模拟材料失配、缺陷、孔隙结构或不均匀性失配的特征应变，M是固体细观尺度的特征域，Ω 是固体中的夹杂子域。因此，可以得到硬化混凝土中粗骨料相互作用而产生的孔结构特征应力场。

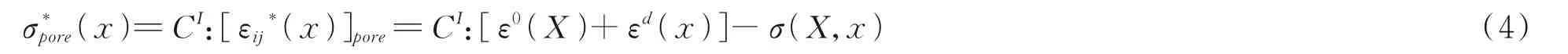
式（4）中CI为包含场的弹性张量。

在无限空间中，孔结构中的特征应变场引起的 诱导位移场可确定为：

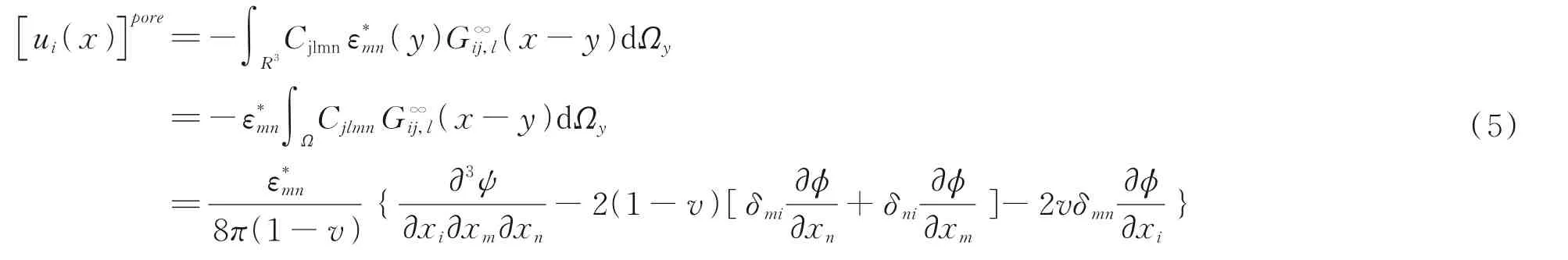
式（5）中[ui(x)]pore是特征应变引起的位移场，CjlmnG∞ij，l(x−y) 是格林变换公式，R3是无限空间域。

对于粗集料锁混凝土，弹性应变场可表示为：

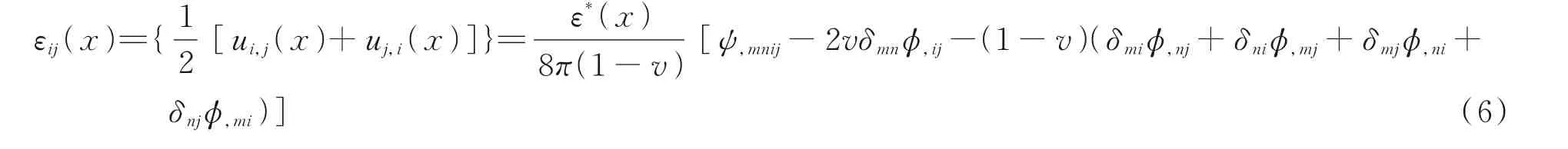
1.2 骨料嵌锁型混凝土的弹塑性本构关系

根据胡克定律，弹性应变与柯西应力的关系为：

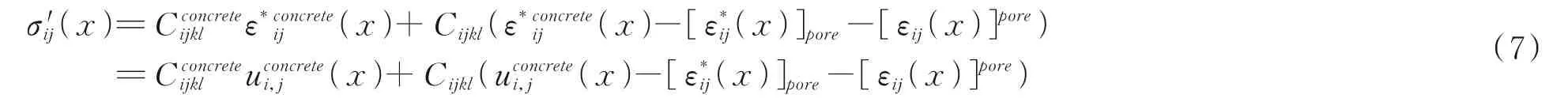
粗集料联锁混凝土弹塑性本构关系的理论解确定为：

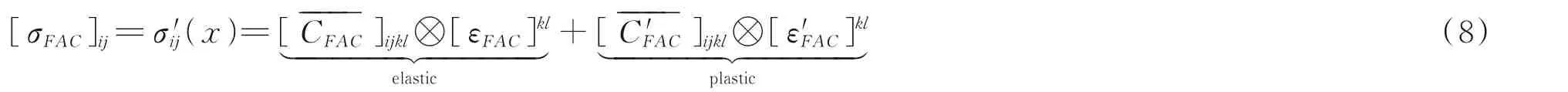
基于广义自洽法理论，推导了弹性阶段混凝土的有效模量，即粗骨料与界面间砂浆的嵌锁对混凝土力学性能的影响。

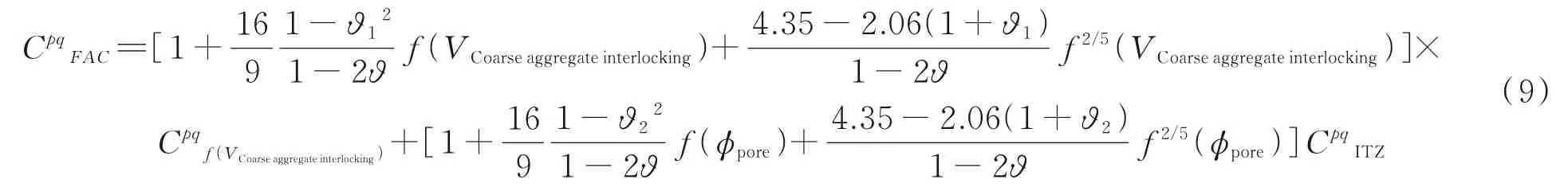
式（9）中CpqFAC为混凝土的有效模量 ，为嵌锁作用下粗骨料的模量为ITZ 的模量，ϑ1为嵌锁作用下粗骨料的泊松比，ϑ2为ITZ 的泊松比，f(VCoarseaggregateinterlocking)是粗嵌锁的密度分布，f(φpore)是孔隙结构的分布表征函数。

1.3 骨料嵌锁型混凝土的断裂韧度方程

利用塑性发展过程中的屈服函数预测材料的断裂过程。因此，基于Gurson 模型建立混凝土的断裂屈服方程为：

式（10）至式（12）中Φ(∑ij，σe，f*(φpore))是混凝土的屈服函数，是宏观应力，σe是等效屈服应力，∑eq是Mises 屈服应力，∑m是静水应力，f*(φpore)是屈服过程中ITZ 的孔隙率分布函数，fc(φpore)是孔合流开始时的孔隙率分布函数，ffra(φpore)是材料断裂时的临界孔隙度分布函数，D＇是载荷作用下的损伤因子，ΔR是ITZ 的孔径变化值，RN是ITZ 的孔径特征值。

根据断裂准则，确定粗骨料嵌锁型混凝土的断裂韧度方程为：

式（13）中G͂FAC为粗骨料混凝土的断裂韧度。

2 实验方案

2.1 原材料及配合比

实验所用原材料为当地普通硅酸盐水泥（P.O 42.5N）细度模量为2.3 的当地河砂，及水等。当地石灰石用作粗骨料，其尺寸为5~25 mm。普通硅酸盐水泥的基本性能及化学组成分别列于表1 和表2，河砂和粗骨料的物理性质列于表3。

表1 水泥的基本性能Table 1 Mechanical properties of Portland cement

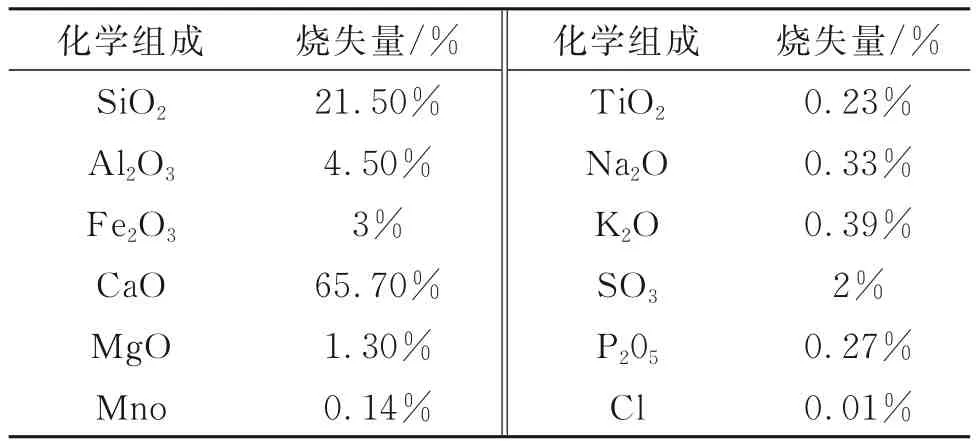
表2 水泥的化学组成Table 2 Chemical properties of Portland cement

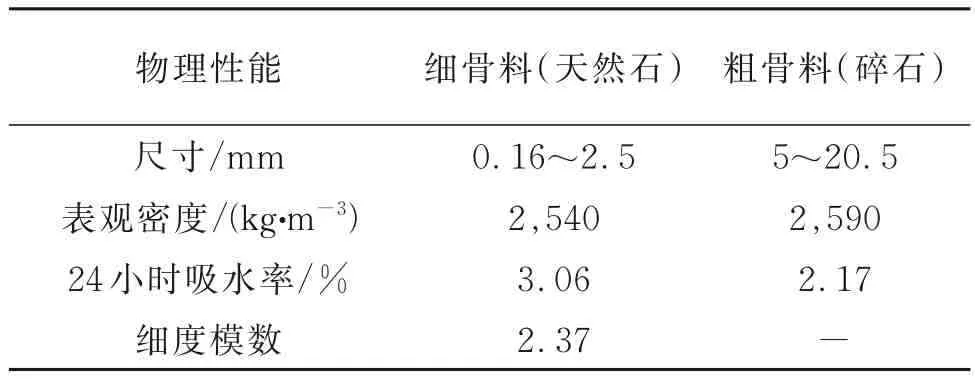
表3 骨料的物理性能Table 3 Physical properties of aggregates

水灰比为0.45，粗骨料按基本骨料体积百分比增加，分别为5%、10%、15%、20%和25%，混凝土配合比列于表4。

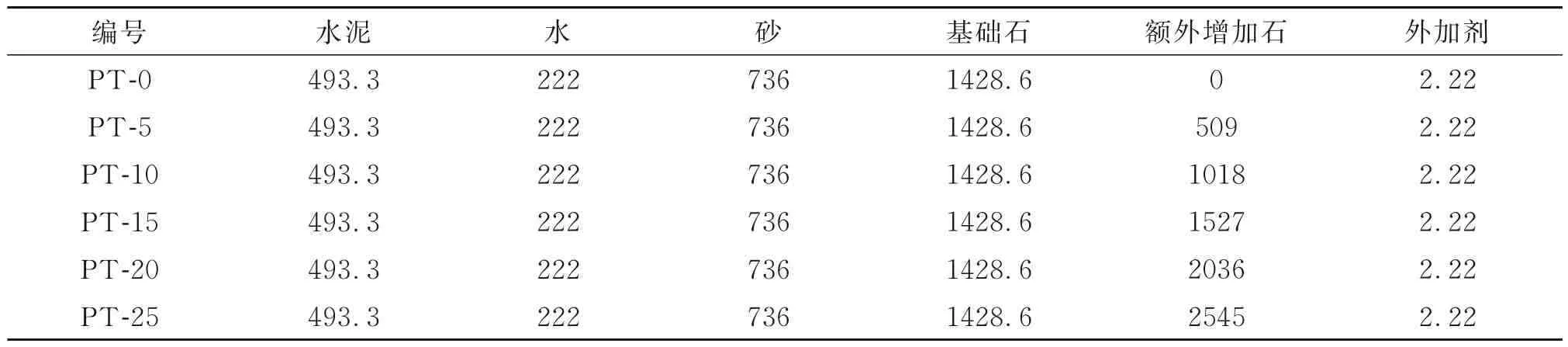
表4 粗骨料混凝土的配合比Table 4 Mixing proportions of coarse aggregate interlocking concrete /(kg·m−3)

2.2 试件的制备与养护

混凝土试件的制备按照规范JTG 3420-2020［19］，混凝土试样尺寸分别为150 mm×150 mm×150 mm（144 件）、100 mm×100 mm×300 mm（108 件）和150 mm×150 mm×300 mm（108件），试样在24 h 后脱模。然后将每个样品置于饱和石灰水中，在室温（即20±2 ℃，RH≥95%）下按GB/T50081-2002［20］进行28 天的养护。

2.3 实验方法

2.3.1 粗骨料嵌锁型混凝土的强度及弹性模量试验

根据GB/T50081-2002［20］，对150 mm×150 mm×150 mm（144 块）试件进行28 天抗压、抗折和轴压强度试验。

按GB/T50081-2002［20］的规定，30%轴压抗压强度应力下的割线模量作为弹性模量值。实验制作的试样尺寸为 100 mm×100 mm×300 mm（108 件）。

2.3.2 粗骨料嵌锁型混凝土的断裂韧性试验

采用缺口三点弯曲梁法，测定粗骨料混凝土的断裂韧度。通过在试样侧面切割，使试样产生裂纹。宽度控制在3±1 mm，长度控制在80±2 mm，结合面与试件成90±0.5 °。具体实验根据GB/T50081-2002［20］进行操作，实验制作的试样尺寸为150 mm×150 mm×300 mm（108 件）。

2.3.3 压汞法（MIP）分析

压汞法是研究水泥基材料孔隙特性最常用的方法。该方法相对简单，通常产生可重复的孔径分布。从这些孔径分布可以推断出总孔径、总孔隙率和理论孔径等重要的特征参数。随着压力的增加，汞被压入混凝土样品的孔隙结构中，汞填充样品后可以得到侵入压力与孔隙半径的关系。对混凝土细颗粒（5 组，每组6 个固体样品）进行压汞试验分析。

3 结果与讨论

3.1 粗骨料嵌锁型混凝土的力学性能

图1 分别为粗骨料嵌锁型混凝土抗压和抗折强度的试验结果。从图1 可见：宏观力学强度，随粗骨料体积率的增大呈现先增大后减少的趋势；当外部粗骨料体积分数为0%~20%时，强度随集料取代率的增加而增加；当粗骨料体积率为15%~20%时，抗压强度和抗折强度达到最大值，分别提高40%和36%；当粗骨料体积率为25%时，宏观力学性能显著降低。这是因为混凝土中粗骨料过多时难以压实，从而降低了机械强度。然而，由于骨料之间的嵌锁效应，最终力学强度仍高于参考值。

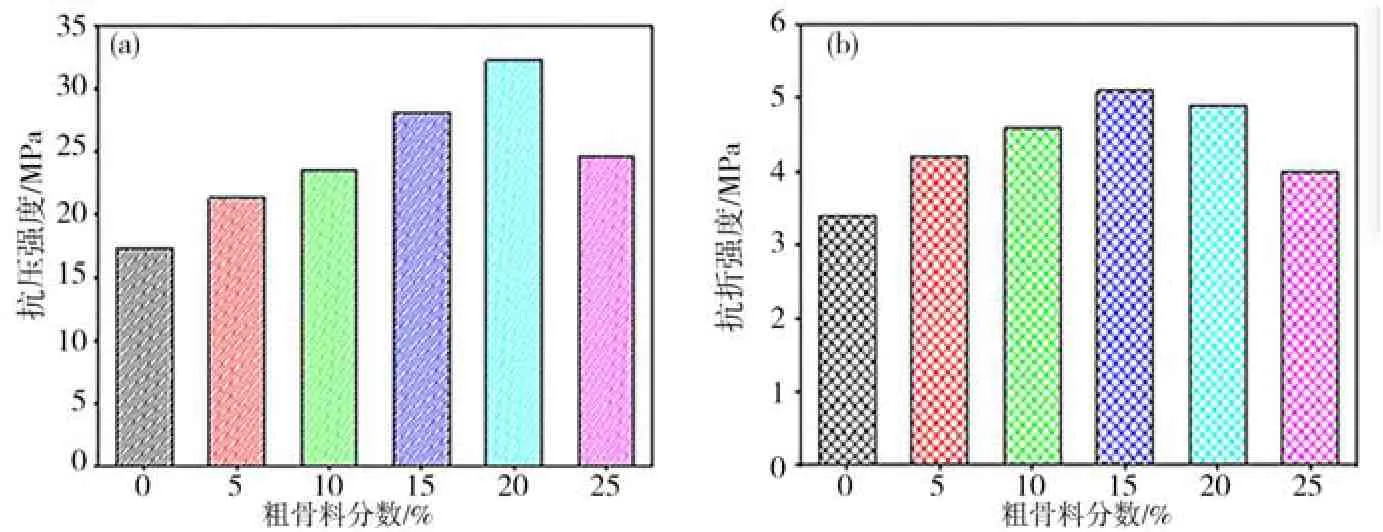
图1 不同掺量下粗骨料嵌锁型混凝土的抗压强度及抗折强度Fig.1 Compressive strengths and flexural strengths of coarse aggregates interlocking concrete subjected to different amount of coarse aggregates

压缩断裂界面形态的对比分析如图2 所示。从图2 可见：粗骨料体积比的增大，促进了混凝土水化过程中骨料相互嵌入和相互咬合的空间分布的形成，也降低了荷载作用下贯穿裂缝的分布概率；当粗骨料体积比为20%时，试件的芯部在压碎破坏时没有明显的裂纹。

图2 不同掺量下粗骨料嵌锁型混凝土的破坏形貌Fig.2 Failure modes of coarse aggregates interlocking concrete subjected to different amount of coarse aggregates under compressive load

图3 为粗骨料嵌锁型混凝土的弹性模量。从图3 可见：当骨料体积增量为5%、10%、15%及20%时，其弹性模量分别比基准组增加3.3%、6.6%，13%和19.8%；当骨料体积为25%时弹性模量开始下降，其变化及演变与上述强度特性的结果相似。

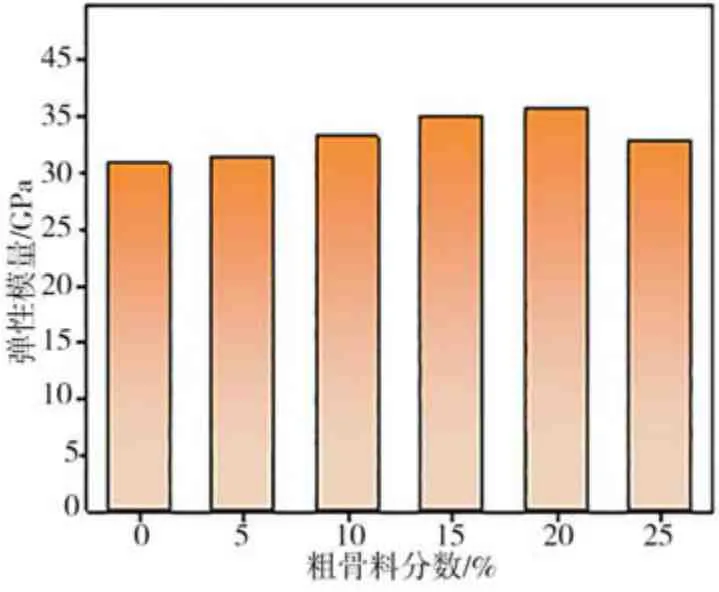
图3 不同掺量下粗骨料嵌锁型混凝土的弹性模量Fig.3 Elastic modulus of coarse aggregates interlocking concrete subjected to different amount of coarse aggregates

3.2 粗骨料嵌锁型混凝土的断裂特性

图4 和图5 分别为粗骨料嵌锁型混凝土断裂试验中的初始断裂载荷、初始断裂韧度和极限断裂载荷的结果。从图4 和图5 可见：与基准混凝土相比，随着骨料掺量的增加，开裂荷载呈现先增大后减小的趋势；当骨料体积增加20%时，初始裂纹荷载开始呈现下降趋势；当粗骨料掺量增加0%~20%时，产生初始裂缝和极限荷载增大，这是因为骨料的增多使混凝土内部的材料填充密实，提高了材料的整体密实度；当增量达到20%~25%时，过多的粗骨料会影响混凝土的和易性，从而降低混凝土的粘结力，产生更多的内部裂缝。这导致混凝土断裂过程中产生了初始裂缝和极限荷载的减少的现象。

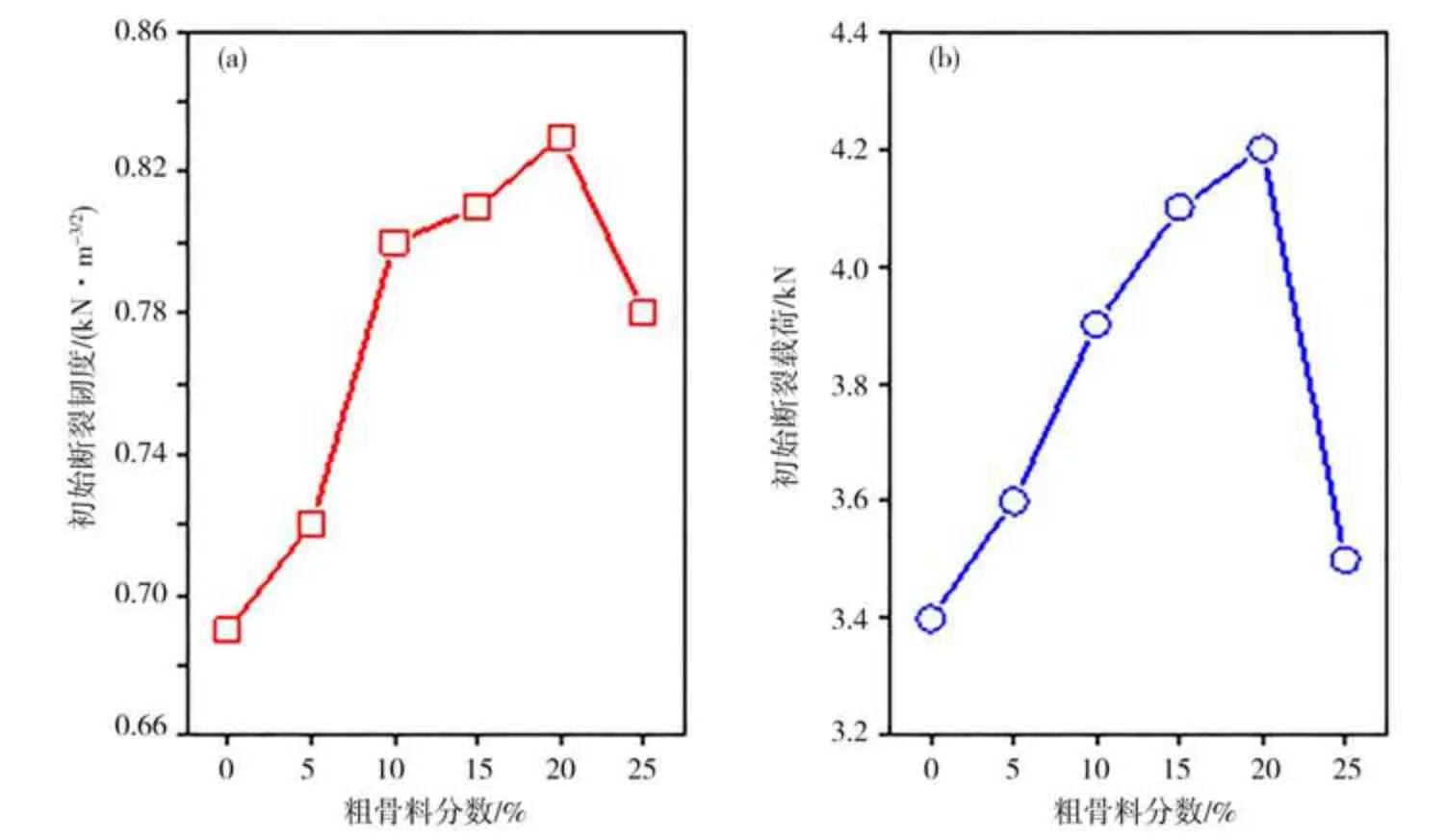
图4 粗骨料嵌锁型混凝土的初始断裂荷载和初始断裂韧度Fig.4 Initiation failure load and fracture toughness of coarse aggregates interlocking concrete

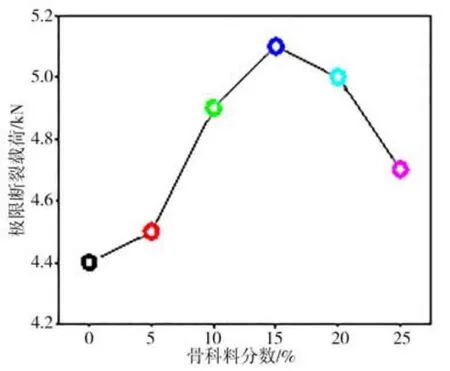
图5 粗骨料嵌锁型混凝土的极限断裂荷载Fig. 5 Ultimate load of coarse aggregates interlocking concrete

根据断裂力学中的经典计算公式，可以得到粗骨料嵌锁型混凝土在不同粗骨料体积增量下的试验断裂能，其结果如图6 所示。从图6 可见：当粗骨料体积为0%~15%时，断裂能呈增加趋势，体积每增加5%，断裂能分别增加12.3%、17.6%和19.4%，这是由于在断裂过程中粗骨料之间形成一定的摩擦力，间接增加了粗骨料与粗骨料及粗骨料与胶凝材料之间的咬合力，从而提高了断裂能；当粗骨料体积分数达到20%时，断裂能呈下降趋势，与15%集料体积分数相比，下降了15.3%；当粗骨料体积增加到25%时，由于压实度的降低，材料间的咬合力开始减小，导致断裂能呈现下降趋势。

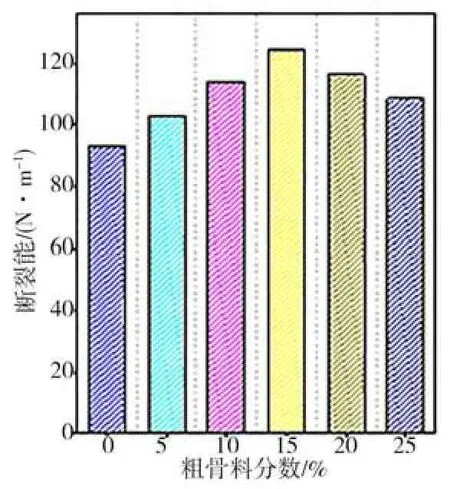
图6 粗骨料嵌锁型混凝土的断裂能Fig.6 Fracture energy of coarse aggregates interlocking concrete

3.3 粗骨料嵌锁型混凝土的孔径分布

图7 为粗骨料嵌锁型混凝土的孔径分布变化曲线，图8 为孔隙率和临界孔径等特征孔隙参数。从图7 和图8 可见：孔径为0~0.1 nm 时，累计进汞量下降速率较快，并且随着粗骨料体积的增加，曲线总体向左移动。同时，峰值（最大孔径）向左移动，且峰值呈减小趋势；随着粗骨料体积的增加，混凝土的孔隙率和临界孔隙率逐渐减小且略有降低，表明适当增加粗骨料的掺量，不仅能起到原有强度骨架的作用，而且能提高混凝土的内部密实度，降低内部孔隙密度，从而提高混凝土的极限强度和抗折强度；但由于和易性的影响和胶凝材料包裹不足，当粗骨料体积增加20%~25%时，孔密度增大，极限强度和断裂能显著降低。综上所述，粗骨料与混凝土孔结构的施工有着重要的关系，孔隙率和临界孔径的变化对断裂韧度和极限强度有显著影响，为理论模拟计算提供了相关的计算参数。

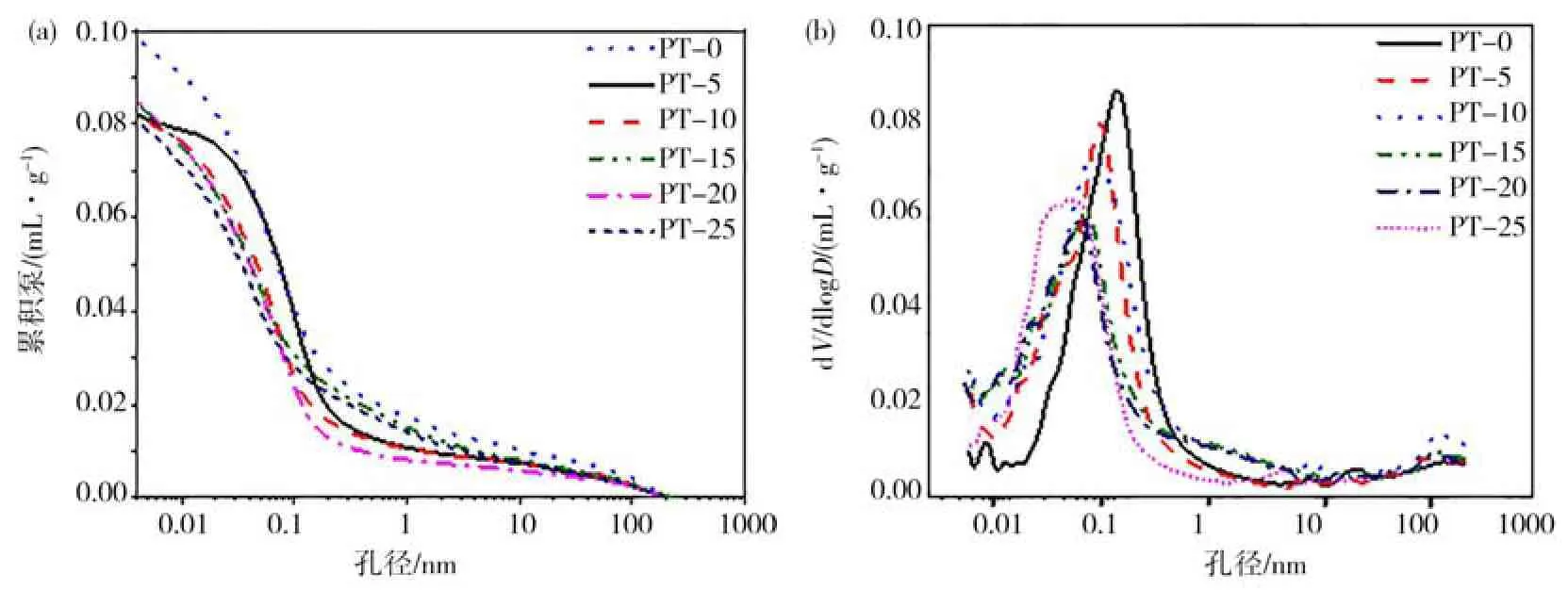
图7 粗骨料嵌锁型混凝土的孔径分布Fig.7 Pore size distribution of coarse aggregates interlocking concrete

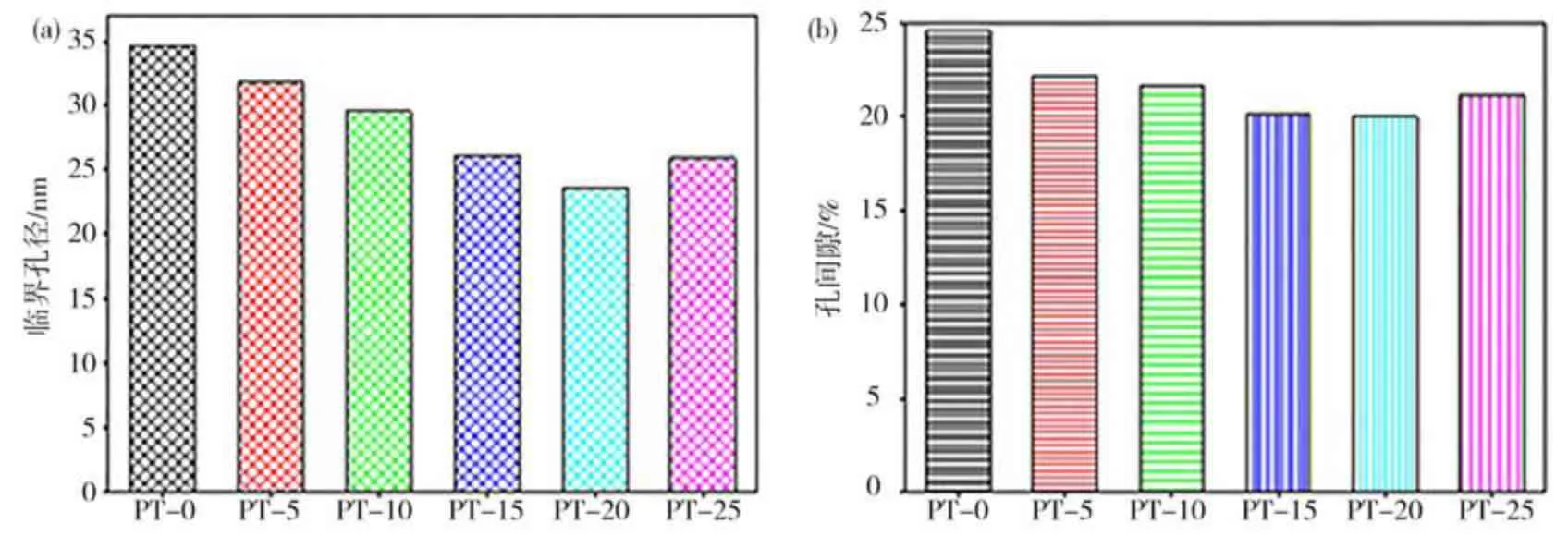
图8 粗骨料嵌锁型混凝土的孔隙参数Fig.8 Pore parameters of coarse aggregates interlocking concrete

3.4 基于细观断裂模型计算的粗骨料嵌锁型混凝土断裂特征

基于建立的粗骨料嵌锁型混凝土的断裂理论模型，对其断裂特性进行理论计算并与实验结果进行了比较，比较结果及误差分析如图9 和图10 所示。综合分析计算与实验对比结果发现：对于抗压强度和弹性模量的模拟，模拟结果均高于试验结果；对于断裂能的模拟，其模拟结果与实验结果具有相同的规律；抗压强度和弹性模量的模拟，随着粗骨料体积的增大计算误差逐渐趋于稳定（3%~4%），粗骨料体积增长较大（大于20%）时计算结果精度不理想，表明计算结果受粗骨料影响且产生较大的波动和误差。对于断裂能的模拟结果，当粗骨料的增加量小于20%时计算误差较小（误差为2%），能较好地反映混凝土断裂过程中断裂能的发展特征，当粗骨料体积增加较大（大于20%）时计算误差很大。如何提高相关计算结果的准确性，是该模型仍需改进和完善的研究内容。综上所述，所建立的细观尺度力学模型具有一定的理论基础和计算精度。

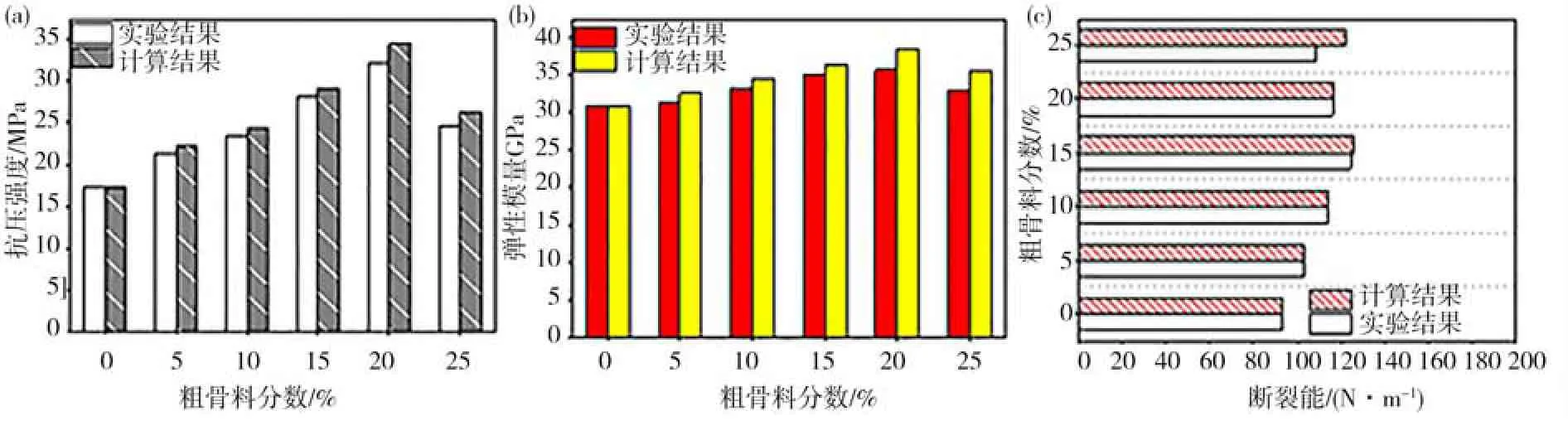
图9 粗骨料嵌锁型混凝土试验与模拟计算结果比较Fig. 9 Comparison of experimental and numerical results of coarse aggregates interlocking concrete

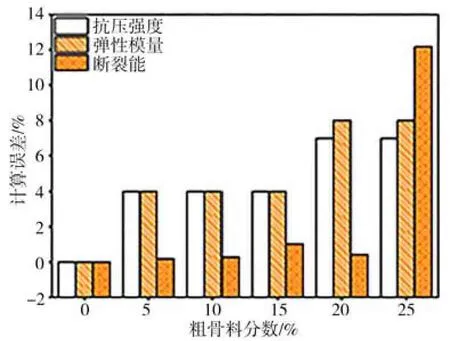
图10 粗骨料嵌锁型混凝土的抗压强度、弹性模量和断裂能的计算误差值Fig.10 Calculated errors of compressive strength，elastic modulus and fracture energy between experimental and numerical results

4 结论

基于细观力学RVE 模型和断裂力学机理，建立了新型细观断裂模型，并将其应用于计算粗骨料嵌锁型混凝土的断裂特性，并得出以下结论。

（1）对混凝土的极限强度和断裂特性进行了试验和理论研究。在一定范围内，粗骨料掺量的增加可以显著提高混凝土的宏观强度和抗折强度。但随着掺量的增加，由于粗骨料过多导致胶凝材料的工作性能降低、凝结硬化降低和孔隙结构分布不均等，使得宏观力学性能下降，但仍高于参考值。

（2）混凝土的力学性能和断裂特性均随着粗骨料体积的增加呈先增加后减小的趋势，当粗骨料体积增量为20%时，抗压强度和弹性模量最高，断裂荷载最大，断裂韧度最强；当粗骨料体积增量为15%时，抗折强度和断裂能最高。

（3）当粗骨料体积增加率小于20%时，抗压强度和弹性模量的模拟结果均高于试验结果，但随着骨料增多，计算误差降低；断裂能的模拟结果规律与试验结果一致，基于建立的细观断裂模型，可以较好地评估和预测粗骨料嵌锁型混凝土的力学响应和发展，其理论计算的结果具有较高的精度。