Optimal Doping Content of Red Emitting Y4GeO8∶Bi3+,Eu3+ Phosphor Designed by Response Surface Methodology
2022-05-23XUShujunCHENJingCHENLiyuanASHRAFGhulamAbbasLIHuijunGUOHai
XU Shu-jun, CHEN Jing, CHEN Li-yuan, ASHRAF Ghulam-Abbas, LI Hui-jun, GUO Hai
(Department of Physics, Zhejiang Normal University, Jinhua 321004, China)*Corresponding Author, E-mail: ghh@zjnu.cn
Abstract: Herein, a more direct method, response surface methodology, is used to predict the strongest red emission of Y4GeO8∶Bi3+,Eu3+ samples. The concentrations of Bi3+ and Eu3+ of the optimal sample were predicted to be 31.03% and 67.36%(in mole ratio), respectively. The optimal sample was prepared and photoluminescent properties were measured and characterized. Y4GeO8∶31.03%Bi3+,67.36%Eu3+ has strongest red emission. The difference between the intensity of experimental value and theoretical value is very small. The color coordinate of the as-prepared sample is (0.645 7, 0.349 0), which is very close to the color coordinate of standard red light (0.670 0, 0.330 0). The luminous color of the sample is pure, and the calculated color purity reaches 98%. What’s more, the internal quantum efficiency of the sample is as high as 72.5%. In a word, this paper provides an approach for searching the optimal doping concentration of phosphors with the strongest luminescence directly, which can be used in exploring all types of co-doped phosphors.
Key words: Y4GeO8∶Bi3+,Eu3+ phosphors; response surface methodology; luminescent intensity
1 Introduction
In the field of solid-state lighting, white light emitting diode(W-LED) has attracted extensive attention because of its high efficiency,no pollution and long service lifetime[1-4]. Generally, W-LED can be made of blue light chip and yellow phosphor, YAG∶Ce3+. However, the lack of red light leads to low color rendering index and high color temperature. In this regard, some researchers have proposed a feasible method for fabricating W-LED using ultraviolet(UV) chip and red, green and blue phosphors[5-6]. No matter which method is used to prepare W-LED, the red-light component is very important.
At present, some researchers are committed to exploring red phosphors[7-8]. For example, Yueetal. reported red-emitting Sr3La(AlO)3(BO3)4∶Eu3+phosphors with high color purity of 92.4%[9]. Guoetal. synthesized red-emitting Na3Sc2(PO4)∶Eu3+phosphors with quantum efficiency of 49%[10]. Wangetal. prepared red-emitting Gd2InSbO7∶Eu3+phosphors with Commission Internationale de L’Eclairage(CIE) of (0.629 0, 0.371 0)[11]. All the red phosphors studied above have good luminescent properties. Usually, researchers change the concentration of doped ions by the control variable method to seek the strongest luminescence. But this traditional method cannot find the strongest luminescence directly. Therefore, some researchers want to explore whether there is a direct way to find the strongest luminescence. Some researchers have found that the response surface methodology(RSM) can be used to determine an optimal value of some problems. And RSM has the advantages, such as displaying the relationships between independent and dependent variables, including error analysis, and saving time and low cost[12-14]. For instance, Lietal. predicted the best conditions to reach the maximum relative density of calcia partially stabilized zirconia by RSM[15]. Luoetal. studied the effects of extraction temperature, extraction time, ratio of water and their interaction on the yield of urea dioxide total polysaccharide by RSM[16]. Theoretically, most of the methods are universal. In other words, RSM is also feasible in the field of luminescent materials.
Due to their stable properties and high solubility of rare earth ions, germanate phosphors have stimulated the interest of researchers in recent years[17-19]. For doped ions, Eu3+is a very excellent activator for red emission, but its intensity is very weak[20-23]. It is necessary to introduce a sensitizer to enhance its luminous intensity[18]. Bi3+is an excellent sensitizer[24-25]. The co-doping of Bi3+and Eu3+can improve the luminous intensity of phosphors[26-28]. Therefore, the phosphor Y4GeO8∶Bi3+,Eu3+was selected as an example to optimize by RSM.
The purpose of this study is to determine the optimal doping concentrations of Bi3+and Eu3+in Y4GeO8∶Bi3+,Eu3+phosphors through uniform design and RSM. Through simulation, the ions concentrations of Bi3+and Eu3+are 31.03% and 67.36%(in mole ratio), respectively. The CIE, color purity and quantum efficiency of Y4GeO8∶31.03%Bi3+,67.36%Eu3+phosphors were further studied. The color purity of the optimal sample is as high as 98%, and its internal quantum efficiency is 72.5%.
2 Experiments
2.1 Sample Preparation
A series of Y4GeO8∶Bi3+,Eu3+phosphors were synthesized by solid-state reaction method. Firstly, the basic materials Y2O3(99.99%), GeO2(99.999%), Bi2O3(99.99%), Eu2O3(99.99%) and H3BO3(99.8%) were weighed conforming to the stoichiometric ratio, in which H3BO3was used as the cosolvent. Secondly, basic materials were ground in a mortar for 30 min. Alcohol was added during the grinding process to help the raw materials mix evenly. The uniformly blended material was then placed in an alumina crucible and sintered for 5 h at 1 400 ℃. Finally, after cooling, the sintered sample was ground into powder for further characterization.
2.2 Characterizations
X-ray diffraction(XRD) patterns were characterized by Rigaku MiniFlex/600 using Cu Kα1 radiation. An Edinburgh FS5 spectrofluorometer with a 150 W Xe lamp was used to examine the samples’ excitation and emission spectra. Samples with the same mass were added into the same sample holders. For spectra measurement, the position of the samples remains unchanged, and the spectrometer parameters remain unchanged for better comparison. Internal quantum efficiencies and temperature-dependent photoluminescence spectra were obtained using FS5 spectrofluorometer with a TCB1402C temperature controller(China) and a SC-30 integrating sphere, respectively.
2.3 Uniform Design and RSM
Uniform design can narrow the experimental range of RSM according to the experimental results. So U9(92) test table was used to design the experiment. RSM was used to determine the best combination of experimental parameters(concentrations of Bi3+and Eu3+) to obtain the strongest luminescence. RSM needs to be reflected in the coding space, so central composite design(CCD) was used to encode the experimental parameters. The data obtained by RSM were analyzed by variance, and the obtained data were judged by T-test and F-test. F-test was used to determine the credibility of the RSM’s equation. T-test is used to determine whether the equation is loss of fitting[12-16].
3 Results and Discussion
3.1 Results and Analysis of Uniform Design
The U9(92) uniform design table is shown in Tab.1. According to the results reported in the literature, the doping concentrations ranges of Bi3+and Eu3+ions are preliminarily selected as 10%-60% and 20%-120%, respectively[18]. Nine samples were uniformly designed according to U9(92), and the doping concentrations of Bi3+and Eu3+ions in each sample are located in column 2 and column 3 of Tab.1, respectively. The integrated intensities of photoluminescence(PL) spectra in Fig.1 are calculated and analyzed. The integrated section is 560-800 nm. The results are presented in the fourth column(Y) of Tab.1. Comparing the results of the samples, it can be inferred that the optimal doping concentrations ranges of Bi3+and Eu3+are 10%-50% and 35%-95%, respectively.
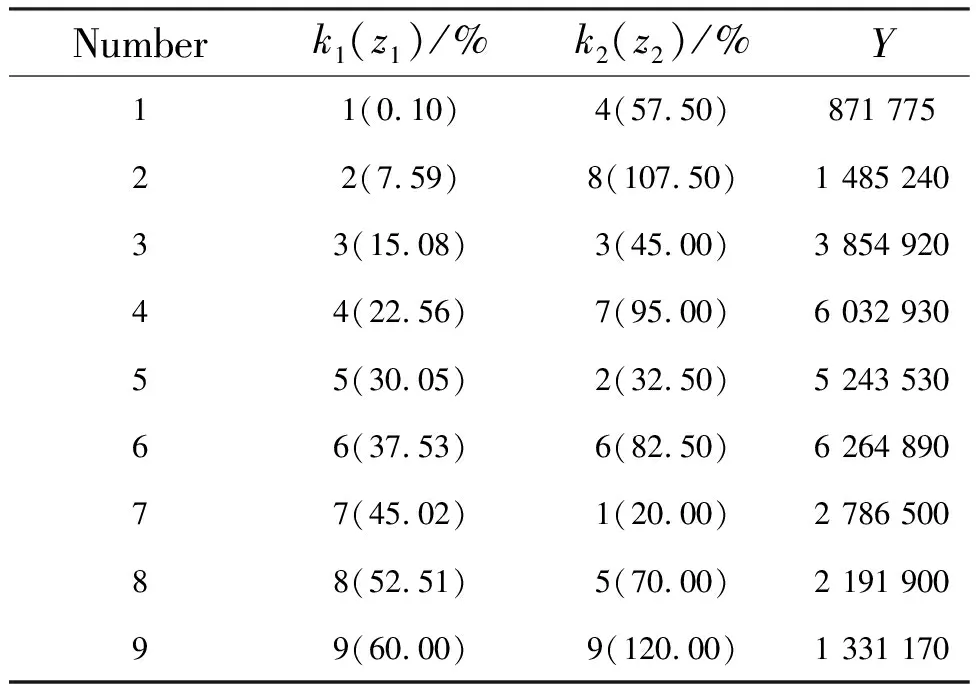
Tab.1 Uniform design table of nine samples, including the concentrations of Bi3+ and Eu3+ and the integrated luminous intensity, where z and k represent the concentration of ions and the serial number of ions in the uniform design, respectively
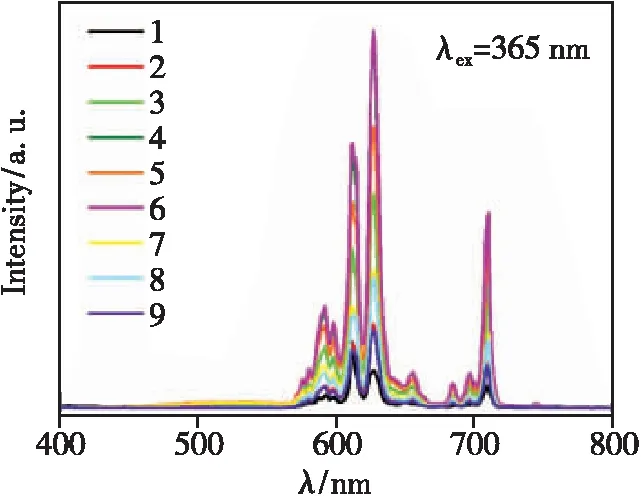
Fig.1 Emission spectra of samples designed by uniform design(λex=365 nm)
3.2 Results and Test of RSM
A mathematical model, quadratic polynomial, is established based on the Tab.3. The coefficients of each factor of the quadratic polynomial are given in the row of“bj”, and the quadratic regression equation of the coding space can be obtained as follow[30]:

Tab.3 RSM table containing the concentrations of Bi3+ and Eu3+, the corresponding samples’ integrated intensity and the corresponding coefficients(r=1.414)
Y=7504884+377659.305k1+169978.18k2-
(1)
Tab.4 shows the variance analysis of the F-test and T-test for the Eq.(1). The sum of squares and degrees of freedom can be obtained according to Tab.4[29]. From the sum of squares and degrees of freedom, we can further judge whether the Eq.(1) is misfit and credible. The calculation is given by the following formulas:

Tab.4 Table of variance analysis via T-test and F-test, in which SR, Sr, Slf, Se and S represent the sum of residual squares, the sum of regression squares, the sum of mismatch squares, the sum of error squares and the sum of total squares, respectively
whereFlf,Frare the loss of fitting test and the degree of confidence test, respectively. It can be seen from the test results that the Eq.(1) does not loss fitting, and the degree of confidence reaches 99%, which proves that the regression model is consistent with the actual situation[12,14,29-30]. The doping concentrations of Bi3+and Eu3+ions corresponding to Y4GeO8∶Bi3+,Eu3+phosphors with the best red luminous intensity can be obtained by converting Eq.(1) to real space.

Fig.2 Emission spectra of 13 samples in Tab.3 designed by RSM(λex=365 nm)
By converting the coding space equation into natural space using the formula in Tab.2, the binary quadratic regression equation between the doping concentration and luminescence intensity of Bi3+and Eu3+in natural space can be obtained. That is, replace the variablekin Eq.(1) with the variablezaccording to the formula in the last row of Tab.2. The conversion result is as following:

Tab.2 illustrates the conversion of experimental parameters between coded space and real space, where z and k represent the concentrations of ions in real space and coding space, respectively[29-30]. Thirteen samples were designed based on Tab.2. The concentrations of Bi3+ and Eu3+ are listed in columns 3 and 4 of Tab.3, in which the values in brackets and not in brackets represent the concentration in natural space and coding space, respectively. After thirteen samples were prepared, their PL spectra were measured. Fig.2 presents that the luminous intensity of each sample is different. The integrated luminous intensities are calculated according to spectra, and the results are shown in the last column of Tab.3.
Y=-12595306.02+799236.47z1+229254.0816z2-
According to the Eq.(4), the ions doping concentration corresponding to the sample with the strongest luminescence can be predicted by genetic algorithm.The concentrations of Bi3+and Eu3+of the optimal Y4GeO8∶Bi3+,Eu3+sample(labelled as Optimal-YGO) are 31.03% and 67.36%, respectively, and the predicted strongest luminescence intensity is 7 528 268. The 3D graph of the Eq.(4) shows the
intensity of the samples more intuitively, as indicated in Fig.3. We can infer the relationship between the luminous intensity of samples and the concentrations of Bi3+/Eu3+. Obviously, when the concentration of one ion is fixed, the luminous intensity will first increase and then decrease with the increase of the concentration of another ion. As shown in the figure, it reveals that the change of concentration of Bi3+has a greater impact on the luminous intensity than Eu3+.

Fig.3 The relationship between luminous intensity and concentrations of Bi3+/Eu3+, where z1/z2 represents the concentrations of Bi3+/Eu3+ and y represents the luminous intensity.
3.3 Characterization of Optimal-YGO Sample
The results of powder XRD patterns of the Optimal-YGO and the standard patterns of Y4GeO8(JCPDS No.21-1446) are presented in Fig.4. The peaks of the sample are essentially consistent with those of the standard card, indicating that the incorporation of Bi3+and Eu3+has little affected the structure of the matrix, and red phosphor is successfully synthesized.

Fig.4 XRD patterns of the Optimal-YGO and the standard card of Y4GeO8(JCPDS No. 21-1446)
The PL spectra of Optimal-YGO were measured in order to further investigate its properties. Fig.5(a) is the excitation spectra(λem=627 nm) and the optimum excitation of the sample is 365 nm. Fig.5(b) is the corresponding emission spectra of the sample. It can be seen that the strongest emission of the sample under the excitation of 365 nm is 627 nm. A series of emission peaks of 565-750 nm come from5D0→7FJ(J=0-4) transitions of Eu3+, respectively[31-32]. After calculation, the integral intensity of the emission spectrum is 7 520 120. Compared with the Eq.(4) simulation results, the error range is small. This proves that the RSM is highly reliable.

Fig.5 (a)Excitation spectrum of Optimal-YGO(λem=627 nm). (b)Emission spectrum of Optimal-YGO(λex=365 nm).
After processing the measured emission spectra data, it is concluded that the CIE of the optimal sample is (0.645 7, 0.349 0). The internal quantum efficiency(IQE) of this sample is as high as 72.5%. Tab. 5 lists some comparison results of as-prepared samples using the control variable method, and Fig.6 shows the corresponding data[18]. The IQE, external quantum efficiency(EQE) and absorption efficiency(Abs) can be given by the following equation[33]:
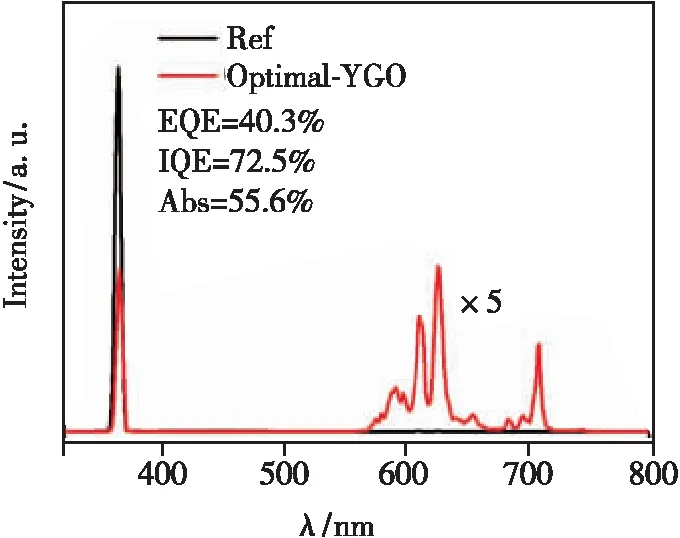
Fig.6 The IQE, EQE and Abs of Optimal-YGO under 365 nm excitation.

Tab.5 Comparison of CIE, IQE, EQE and Abs of sample Y4GeO8∶25%Bi3+,65%Eu3+ and sample Optimal-YGO under 365 nm excitation, the third line is the CIE of the standard red light
(5)
(6)
(7)

The color purity(Pcolor) of the sample can be studied by the following Eq.(8) to further investigate the quality of red emission of the sample[34-35]:
(8)
where (x,y), (xi,yi) and (xd,yd) represent the chromaticity coordinates of the light source under test, equal-energy reference illuminant, and dominant-wavelength point, respectively. In this work, (x,y)=(0.645 7, 0.349 0), (xi,yi)=(0.333, 0.333) and (xd,yd)=(0.650 7, 0.349 3). As a result, the color purity of YGO is about 98%, which is excellent compared with some reported phosphors, such as Sr3La(AlO)3(BO3)4∶Eu3+(92.4%) and Na3Sc2(PO4)3∶Eu3+(87%).
The thermal stability of the optimal sample Optimal-YGO was characterized by temperature-dependent emission spectra. Fig.7(a) summarizes the change of the spectra of the sample with temperature. It can be seen that as the temperature rises, the sample’s spectral intensity decreases. The normalization curve of the change of spectral intensity of the sample with the change of temperature is presented in Fig.7(b). From the figure, the spectral intensity at 443 K is reduced to 50% of that at 293 K.

Fig.7 (a)Temperature-dependent emission spectra of Optimal-YGO(λex=365 nm). (b)Normalized curve of luminous intensity with temperature.
Fig.8 displays the change of sample color coordinates with temperature. It can be seen that the color change of the sample is not obvious with the change of temperature. The insert shows the change of specific color coordinates of the sample.

Fig.8 CIE chromaticity diagrams of Optimal-YGO with temperature(Insert is specific data of color coordinates)
4 Conclusion
In this work, we successfully predicted the sample with the strongest luminescence through RSM more directly. The optimal concentrations of Bi3+and Eu3+were 31.03% and 67.36%, respectively. The optimal sample was successfully prepared. According to the measurement and calculation, the CIE of Optimal-YGO is (0.645 7, 0.349 0), the color purity is 98%, and the IQE is 72.5%. The above results not only show that Optimal-YGO has great application potential in the preparation of UV excited W-LED, but also show that RSM can predict the optimal doping contents of co-doped phosphors with the strongest luminescence.
Response Letter is available for this paper at:http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL. 20220021.
杂志排行
发光学报的其它文章
- A Simple Method to Enhance Performance of Inverted Planar Perovskite Solar Cells by Using PEDOT∶PSS Doped with DMSO as Hole Transport Layer
- 低温808 nm高效率半导体激光器
- Sn2+-Mn2+共掺杂Gd2O3-Al2O3-SiO2玻璃光致发光性能与能量传递
- 硫化锌电致发光材料在智能可穿戴领域研究进展
- 电子阻挡层Al组分对GaN基蓝光激光二极管光电性能的影响
- High-efficiency Blue Phosphorescent OLEDs Based on Mixed-host Structure by Solution-processed Method
