基于井下巷道网络与定位设备数据联合拓扑的井下精确定位系统实时定位纠偏算法

周 翔，韩燕南，周嘉欣

（1.中煤科工集团常州研究院有限公司，江苏 常州 213000；2.天地（常州）自动化股份有限公司，江苏 常州 213000）

人员精确定位对于实时监控井下人员数量、人员动态分布、生产指挥调度等方面具有重要意义[1-2]。在煤矿井下，由于定位接收器本身的系统误差，以及复杂的井下巷道对于定位信号的反射、遮挡等因素的影响，导致定位测量数据与真实值存在偏差，这就造成在定位系统中出现人员偏离巷道的情况，无法准确显示人员当前所处巷道位置，因此需要对出现定位偏移问题的人员进行纠偏处理。地图匹配是目前常用的定位纠偏方法[3-4]，常见的地图匹配算法包括最短距离[5]、投影[6-8]、基于网络拓扑结构[9-12]、基于隐马尔可夫模型[13]以及基于D-S 证据推理[14-16]等地图匹配算法。最短距离地图匹配是一种基础的匹配方法，逻辑简单、速度快、实时性好，但匹配准确率较低且稳定性差[3,5]；投影地图匹配计算速度快，实时性好，在一定程度上可以提高目标的定位精度，但在道路网络复杂的情况下，匹配精度和稳定性均会降低[7-8]；基于网络拓扑关系的地图匹配算法准确率和可靠性高，实用性强，适用于复杂的道路网络环境，但缺点在于计算耗时较大[9-10]；基于隐马尔可夫模型的地图匹配算法将车辆GPS 轨迹点位置作为HMM中的观察变量，将车辆实际所在位置作为HMM 中的隐藏状态变量，通过实际数据训练模型再进行真实位置的预测，适用于相对简单的道路网络场景中[13]；基于D-S 证据推理的地图匹配算法不使用历史轨迹点信息，单个点匹配错误不会对下一个定位点的匹配产生太大影响，但随着道路越来越密集会降低匹配结果的准确率[14-16]。

提出了一种基于井下巷道网络与定位设备数据联合拓扑的实时定位纠偏算法，首先构建出巷道网络与定位设备之间的拓扑关系，并基于拓扑关系，根据人员定位信息快速准确定位其所在巷道，再利用纠偏计算模型对实现人员实时定位坐标进行纠偏解算，实现具有实时性的人员定位纠偏效果。

1 井下定位纠偏算法

1.1 算法基本思路

算法思路示意图如图1。

图1 算法思路示意图Fig.1 The design idea of algorithm

假设人员1 根据定位设备的测量结果被定位在4 条巷道中间，距离巷道BE 最近，如果根据距离最近原则来定位，容易将人员1 定位在巷道BE 上，但如果人员1 实际由定位器1 定位，而定位器1 与巷道AB 存在唯一确定关系，所以人员1 的真实位置应该在巷道AB 或者相邻巷道BC 上。如果人员1 由定位器2 定位，根据定位器2 和巷道的对应关系可知，人员1 的真实位置应该在巷道DE 上。因此实现井下人员实时位置纠偏的关键点在于如何确定巷道网络与定位设备之间的唯一映射关联，以及高效的纠偏计算模型。

1.2 算法设计描述

根据算法基本思路的分析，设计的实时定位纠偏算法主要包括井下数据拓扑关系构建、巷道定位和纠偏计算3 个部分。

1）井下数据拓扑关系构建。井下数据包括巷道中线点数据、巷道中线数据和定位设备数据。设计的井下数据拓扑关系有2 类：①巷道网络拓扑结构：利用中线点数据和中线数据计算出巷道网络；②巷道-设备拓扑关系：利用中线数据和定位设备数据进行拓扑计算，确定定位设备与巷道的唯一映射关系。通过构建出的拓扑关系将离散的定位设备数据和巷道数据重新组织关联，这样既可利用巷道ID 唯一确定定位设备，又可利用设备ID 唯一确定巷道，便于加速后续的巷道定位计算。井下数据拓扑结构如图2。

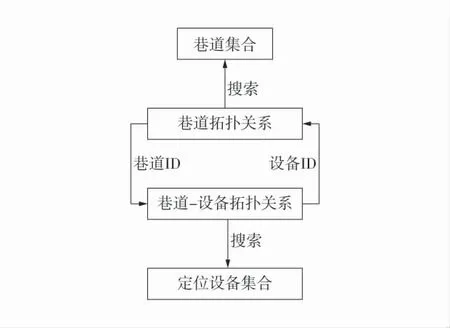
图2 井下数据拓扑结构Fig.2 Topology of mine and equipment data

2）巷道定位。准确定位人员所在巷道是保证纠偏计算准确率的前提。实现巷道定位需要构建人员的潜在定位巷道，再根据人员的定位信息从潜在定位巷道集合筛选最佳定位巷道。巷道定位流程如图3。

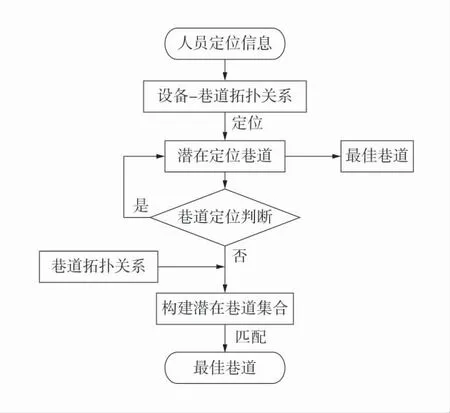
图3 巷道定位流程Fig.3 The flow of mine positioning

3）纠偏计算。纠偏计算的核心在于建立空间坐标纠偏解算模型，该解算模型是将定位设备对人员的测距信息、井下数据拓扑关系和巷道定位结果作为输入参数，由模型自动计算出人员位置纠偏坐标，以代替误差较大的原始定位坐标，由此实现对偏离巷道人员的纠偏。

2 算法设计及实现

算法的设计由井下数据拓扑关系构建和坐标纠偏解算2 部分组成。算法流程设计如图4。

图4 算法流程设计Fig.4 The design flow of algorithm

具体设计思路为：在构建井下数据拓扑结构阶段，分别计算出巷道拓扑网络和巷道-设备拓扑关系，利用这2 个拓扑结构将离散的数据组织关联；在坐标纠偏解算阶段，先利用巷道拓扑网络和巷道-设备拓扑关系确定人员的最佳定位巷道，再将人员测距信息、测距信号偏离量和定位巷道的两中线点作为参数输入纠偏解算模型中计算出纠偏坐标，最终完成纠偏过程。

2.1 井下数据拓扑关系构建

1）巷道网络拓扑关系。每条巷道由相互离散的中线点构成，因此可利用巷道中线点之间的邻接关系构建巷道网络拓扑结构。构建中线点之间邻接关系首先需要计算出井下巷道之间的相交点，合并交点，并且为每个巷道中线点赋值唯一标识，再根据巷道网络之间的相交关系，将每个中线点与其所有邻接点的唯一标识一一关联，完成巷道网络拓扑结构的构建。巷道网络拓扑关系模型如图5，使用字典存储这类拓扑关系模型，通过中线点的坐标或者ID 可快速查找与当前中线点存在邻接关系的所有中线点。

图5 巷道网络拓扑结构Fig.5 Topological structure of mine network

2）巷道-设备拓扑关系。利用定位设备数据与巷道数据构建出巷道-设备拓扑关系，确定设备与巷道之间的唯一映射。通过在巷道-设备拓扑关系网络中匹配人员定位数据中的定位设备信息可快速定位出人员位置纠偏的最佳巷道。巷道网络-设备拓扑结构如图6。

图6 巷道网络-设备拓扑结构Fig.6 Topological structure of joint mine network and equipment

2.2 坐标纠偏计算流程

实时定位纠偏算法的实现流程如下：

第1 步：人员初始坐标偏移差判断。人员定位偏移差如图7。

图7 人员定位偏移差Fig.7 Calculation of personnel positioning deviation

因为每条巷道都是由2 个相互离散的巷道中线点构成的，所以选择定位巷道中的其中1 个中线点作为计算基准点S，另1 个关联中线点为P，则通过式（1）计算出人员T 初始坐标与巷道中线的偏移角度θ，然后利用偏移角度θ 计算出人员与巷道中线的偏离值Dc，如果Dc小于巷道半径距离r，则将当前的人员实时位置直接投影至巷道中线上，否则进入第2 步。

第2 步：测距偏离计算。测距偏离计算如图8。

图8 测距偏离计算Fig.8 Calculation of distance measurement deviation

由于纠偏的结果是将人员定位至巷道的中线上，而在实际中，定位设备被安装在巷道墙壁一侧，因此测距信号相对于巷道中线存在一定夹角，因此在纠偏计算前需要分别计算出定位设备在巷道中线上的投影坐标，以及人员测距相对于巷道中线的偏移量。设D 为测距，S、P 分别为两测距方向所对应的两中线点，R 为定位设备，R 在由点S 和P 构成的巷道上，θ 为测距信号与巷道的偏离角（人工配置），式（3）可计算出定位设备R 的投影坐标Rp，式（4）计算得到测距偏离量Dp。

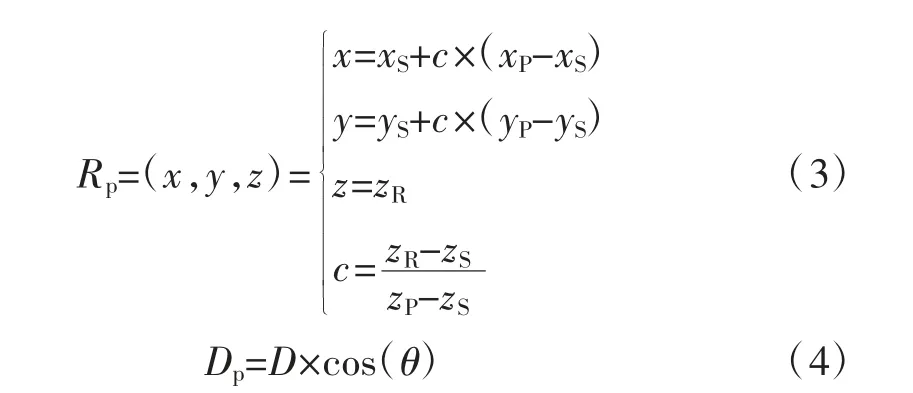
第3 步：巷道定位判断。巷道定位判断如图9。

图9 巷道定位判断Fig.9 Judgment of mine positioning

判断人员测距偏离量Dp是否超出定位设备与测距方向中线点距离的范围。图9 中黑色虚线框内为与测距方向S 相关联的巷道中线点集合。式（5）中的S 是测距方向的中线点，Rp为定位设备在巷道中线上的投影坐标，L 为定位设备的投影坐标Rp与测距方向点S 的间距，C 为计算结果值。

第4 步：完成纠偏计算。

3 试验测试

西北某煤矿的井下巷道情况复杂，井下人员初始定位偏离巷道的现象较为严重，对于实时定位纠偏的需求较为迫切，因此被用作试验对象。分别从实时性、巷道定位精度和纠偏坐标精度3 个方面对所提出的实时定位纠偏算法进行试验。

将实时定位纠偏算法以后端服务的方式嵌入公司开发的井下人员精确定位系统中。试验环境如下：①操作系统：Windows Server；②硬件配置：Core i7-10700F 2.9GHz、16GB RAM；③开发环境：C#、VS2019；④开发平台：Windows10。

3.1 实时性试验

对实时定位纠偏算法的实时效果进行测试，实时性试验分成拓扑计算耗时和纠偏计算耗时2 部分。试验对象包括543 个中线点、127 个定位设备和120 个随机定位数据。将算法部署至现场持续运行一段时间得到的实时性试验结果见表1。

表1 实时性试验结果Table 1 Results of real-time tests

试验结果显示，提出的单人实时纠偏算法平均耗时在0.002 5 s 左右，构建数据拓扑关系的耗时在0.188 s 左右，具有较好的实时效果，能够满足井下人员精确定位对于纠偏的实时计算需求。

3.2 巷道定位精度试验

巷道定位精度试验是对算法将人员定位到实际所在巷道上的准确率进行测试。试验的样本数据与实时性实验保持一致。巷道定位精度试验结果见表2。

表2 巷道定位精度试验结果Table 2 Results of mine positioning accuracy experiment

其中，一次定位是指人员被定位在定位设备所在的巷道上，在试验中，这些人员的巷道定位准确率为100%；多次定位为人员被定位在了定位设备所在巷道的周围巷道上，定位准确率约为94%，试验结果显示，每次迭代计算出的潜在定位巷道数量为1 时，定位精度为100%，当潜在定位巷道数量大于1 时，设定位巷道与其余潜在巷道的方位角度差为β，如果β 大于30°，巷道定位全部准确，如果β 小于15°，巷道定位准确率约为86.7%，如果β 介于15°～30°，巷道定位准确率约为94.1%。多次巷道定位情况的试验结果统计如图10。

图10 多次巷道定位情况的试验结果统计Fig.10 Statistics of experimental results of multiple mine positioning

根据试验结果的分析，当人员测距在定位设备范围内或者潜在定位巷道数量为1 时，算法的巷道定位准确率最高，当潜在定位巷道数量大于1 时，且存在于最佳定位巷道的方位夹角过小的巷道时，定位精度有所降低，但定位精度能够保持在85%以上，总体的巷道定位精度较好，该算法在面对多巷道关联的复杂情况下具有一定的鲁棒性。

3.3 定位纠偏精度试验

纠偏前后效果对比如图11。图11（a）为试验煤矿现场的井下人员精确定位系统中人员原始定位效果，图11（b）为人员的原始定位经过算法纠偏后的效果，所有发生定位偏离的人员均已被准确纠偏。根据现场对于实时定位纠偏算法的实验反馈，表明该算法具有较好的稳定性，纠偏效果明显，能够保持较高的准确率和实时性效果。

图11 纠偏前后效果对比Fig.11 Comparison of the effects of personnel positioning correction

4 结 语

针对煤矿井下人员定位易受硬件系统测算误差以及复杂巷道条件的影响，从而产生定位偏移的问题，研究并实现了一种基于井下数据拓扑结构的实时定位纠偏算法。试验结果表明：该算法的拓扑构建耗时低于0.2 s，平均纠偏计算耗时约为0.002 5 s，对坐标偏离的人员巷道定位准确率超过90%，坐标纠偏计算平均误差较小，具有较高的纠偏准确率和实时性，同时在复杂井下巷道条件下表现出良好的鲁棒性，能够满足井下人员实时精确定位的需求。