基于模糊专家系统与IDE算法的UCAV逃逸机动决策
2022-05-23谭目来丁达理吕丞辉
谭目来, 丁达理, 谢 磊, 丁 维, 吕丞辉
(空军工程大学航空工程学院, 陕西 西安 710038)
0 引 言
随着现代战争中无人机的广泛运用,未来战场使用无人机进行制空权作战成为可能。为提高无人作战飞机(unmanned combat air vehicle, UCAV)空战效能,对UCAV的自主空战机动决策显得尤为重要。当前,自主空战决策方法主要可分为3类:基于机动动作库的博弈论方法;基于优化理论的机动决策方法;基于人工智能的机动决策方法。
基于机动动作库的博弈论方法通过建立机动评价函数,得到机动动作得分博弈矩阵,从而选出最优机动动作,但其机动动作固化,很难做到对当前空战状态自适应。
基于优化理论的机动决策方法包括动态规划算法、智能优化算法、统计理论等。但基于优化理论的机动决策方法得到的机动轨迹战术性较差,轨迹不易被认同。
基于人工智能的机动决策方法主要包括神经网络法和强化学习法。神经网络法决策实时性好,但需要大量样本训练,样本数据的产生不够真实。强化学习法需要样本少,但训练时间长。
为同时具备机动轨迹战术性和对空战状态自适应,本文提出一种基于模糊专家系统与改进差分进化算法(improved differential evolution, IDE)相结合的UCAV逃逸机动决策方法,其框架如图1所示。最为关键的机动决策过程为:首先,根据飞行员空战知识提取,根据双方态势建立模糊专家系统,输出模糊机动动作,根据要达到的模糊动作,对当前控制量的变化量的取值区间进行约束,在取值区间内根据双策略竞争的可选外部存档差分进化算法(external archiving differential evolution algorithm with dual strategy competition, DSC-JADE)进行寻优,得到下一时刻的控制量。其中,机动决策整体评价函数为通过非参量法建立的指标函数。此方法能缩小寻优范围,提高机动决策的实时性,并且得到的飞行轨迹可用空战知识解释。
1 滚动时域机动决策模型
1.1 基于滚动时域的最优控制模型
滚动时域控制(receding horizon control, RHC)是20世纪70年代提出来的一种控制方法,滚动优化把整个RHC任务过程分为一个个相互重叠(单步预测时是不重叠的)但不断向前推进的优化区间,称为滚动时域。在某一滚动时域的开始,用系统的当前状态作为初始条件,在线求解该有限时域开环最优控制问题,得到最优控制序列。RHC原理如图1所示。
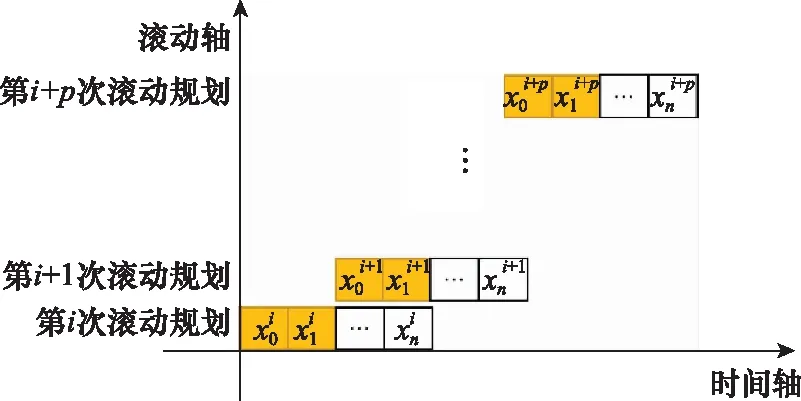
图1 RHC原理
将机动决策问题采用滚动时域控制离散化后得到其数学描述为
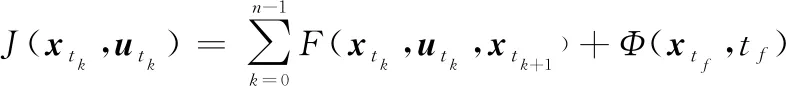
(1)
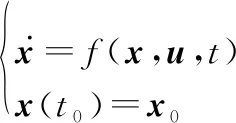
(2)
()∈
(3)
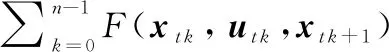
1.2 系统状态方程描述
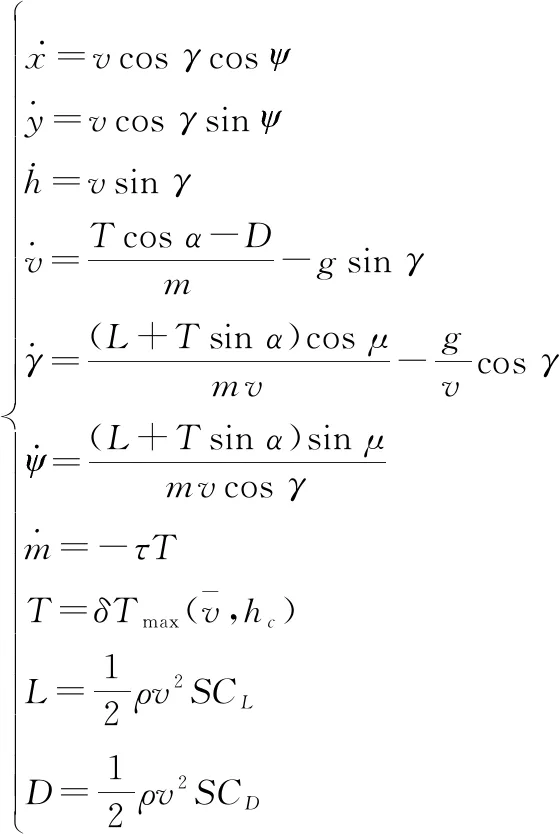
(4)
式中:为重力加速度;,,分别表示发动机推力、空气阻力、升力;=1225-9300为空气密度;为UCAV参考截面积;,分别表示升力系数和阻力系数;为燃料消耗系数;为发动机最大推力。
控制量:=[,,],,,分别表示迎角、航迹滚转角和油门设置。

为区别追击机与UCAV,分别以下标和表示双方。
本文采用F-4“鬼怪式”战斗机的相关参数及气动数据,以保证决策的真实性和高可靠性。
在文献[14]中,采用了以、、即切向过载、法向过载和滚转角为控制量的三自由度模型,其相较于=[,,]为控制量的模型而言,首先后者更贴近飞行员对飞机的控制,是相对于过载模型更底层的控制输入,其次过载模型难以对过载变化进行合理的约束,即过载变化约束不仅和=[,,]等有关,且与推力、升力、阻力等因素有关,不是固定不变的值,因此难以设置过载变化率约束,相比较而言,=[,,]模型的变化率Δ=[Δ,Δ,Δ]的约束可设置为定值。
1.3 指标函数建立
在本文中,由于讨论的是逃逸机动决策,因此只讨论在不利被尾追态势初始条件下,且UCAV以逃逸为主要目的情况下决策因子指标函数的建立。
如果使用以往建立的态势决策因子,会导引UCAV完成对攻击机的攻击占位,主动接近敌机,达不到逃逸的目的。因此,需要建立全新的态势决策因子计算公式,使UCAV尽量保持在导弹攻击区外,且尽量远离攻击机。
131 角度态势决策因子
根据文献[15]可知,在以空空导弹为机载武器的情况下,若UCAV处于雷达扫描探测区中心区域时,常使用直线规避机动。若UCAV处于攻击机雷达扫描探测区侧翼时,常采用正切规避机动。
据此对追击机的雷达天线调整角进行划分,图2为UCAV与追击机相对态势图,当≤30°时,UCAV采用直线规避机动最优,当>30°时,UCAV采用正切规避机动最优。由于正切规避机动未考虑攻击机速度方向,因此对其做出改进,使UCAV速度方向垂直于攻击机速度方向时为UCAV最优机动方向。
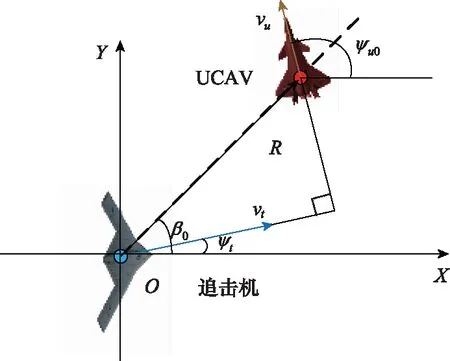
图2 qt>30°时UCAV水平面最优航迹偏角示意图

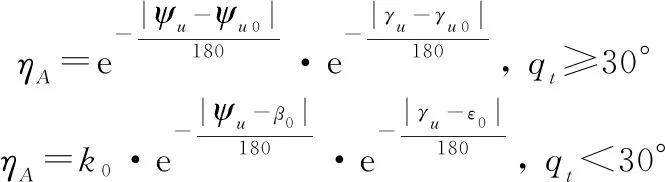
(5)
式中:为目标线矢量的航迹偏角;为目标线矢量的航迹倾角;为压缩系数,即UCAV处于雷达扫描探测区中心区域的角度态势值应小于在侧翼的态势值。
132 距离态势决策因子
取UCAV在导弹攻击范围内时,距离态势决策因子值为0,距离大于导弹最大发射距离时越远值越大,距离小于导弹最小发射距离时越靠近追击机值越大。
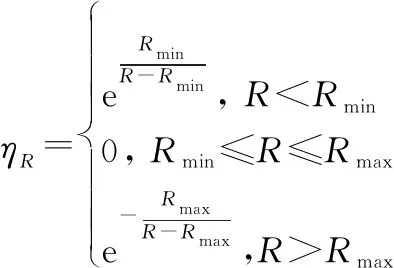
(6)
其中,导弹攻击距离解算由文献[16]确定,即

(7)
式中:和为UCAV相对追击机的离轴方位角和进入角。
133 高度态势决策因子
根据以红外空空导弹为武器的空战形式,UCAV应尽量避免处于追击机最佳攻击高度差附近,同时,UCAV应保持一定的飞行高度,据此建立高度态势决策因子计算函数:
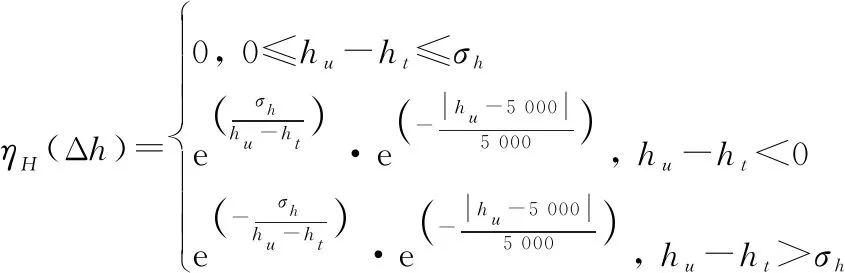
(8)
式中:为追击机攻击目标最优高度差。
134 速度态势决策因子
在UCAV处于逃逸态势下,其速度要尽可能大于追击机,据此建立速度态势决策因子计算函数:
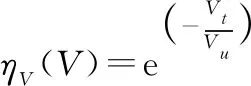
(9)
135 机动决策整体评价函数
=[04,04,01,01]·[,,,]
(10)
其中,系数由文献[17]中的不利态势确定。
假设每一次决策之间的时间是固定的,对于每一次决策,则其任意时刻机动决策求解变为
(,,+1)=(+1)-()=
(,+1,,)-(,,,)=
((,,+Δ,),,)-(,,,)
(11)
式中:(+1)为+1时UCAV的态势值;()为时UCAV的态势值。由于+1时刻UCAV态势值由UCAV状态,+1和追击机状态,计算得到,而,+1由状态方程(,,+Δ,)计算得出,因此决策过程即为对控制量变化率Δ的求解。整个决策过程要使性能指标( , )最大,即为求解控制量变化率序列Δ=[Δ,Δ,Δ](=0,1,…,-1),使其最大。
2 模糊专家系统

2.1 机动动作库
本文采用文献[20]中对基本机动动作库进行拓展之后的拓展机动动作库,如图3所示。由于本文采用的模型与其不同,因此不能应用其建立的控制算法,而是将控制变量和飞行动作之间进行解耦,再根据当前状态确定控制量变化率的正负,达到对寻优范围的约束,从而能够飞出想要的机动动作。由于篇幅有限,在此不加以赘述。
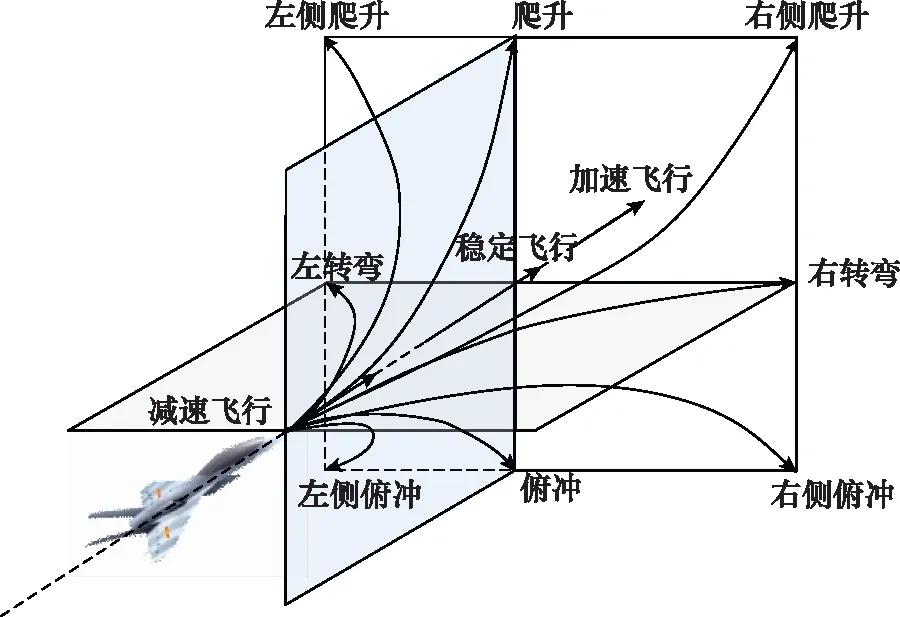
图3 拓展机动动作库
2.2 基于模糊推理的专家系统
当前专家系统主要应用于故障检测方面,而在机动决策方面有关文献较少,且对于专家系统的建立也语焉不详,在文献[10]中,采用滚动时域决策作为专家系统失效时的补充,但对于机动决策的专家系统知识库的建立没有说明,而是简单搭建了框架。在本文中对于知识库的建立给予详细说明。
221 模糊专家系统整体结构
根据在专家系统中知识表达方式的不同,目前的专家系统大致可以分为基于规则的专家系统、基于框架的专家系统、基于模型的专家系统3种情况。
产生式规则是专家系统中常用的知识表示方法,又称为规则表示法,通常用于表示具有因果关系的知识,其基本形式如下:If P, then Q,或者可表示为 P→Q。其中,P代表条件,即前件,如前提、原因等;而Q代表结果,即后件,如结论、后果等,其含意为如果前提P被满足,则可以推出结论Q。亦称为If-Then规则。
文献[22]一文指出,对于复杂系统难以用结构化数据来表达,如果全部用规则的形式来表达,不仅提炼规则相当困难,并且规则库也相当庞大和复杂,容易产生组合爆炸。针对这一情况,引入模糊数学,首先对输入参数进行模糊处理,同时将单一专家系统解耦为多个小规模专家系统,建立了如图4所示的基于模糊推理的专家系统结构图。
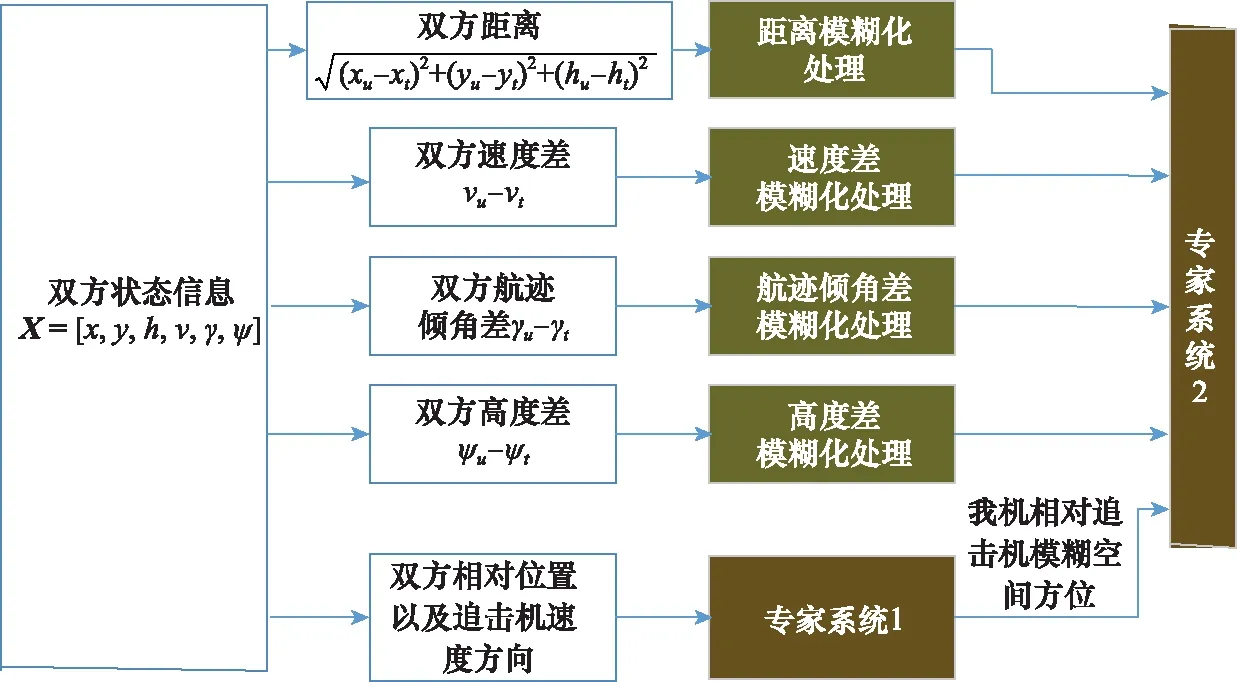
图4 基于模糊推理的专家系统结构图
其中,专家系统1用于根据双方坐标以及追击机航向确定我机相对于敌方模糊的方位。考虑到我机相对敌机处于不利态势,模糊输出分为正前方、左前方、右前方、正上方、左上方、右上方、正下方、左下方、右下方。首先需要计算追击机与我机之间的视线角,具体的设计如表1所示。

表1 专家系统1设计
2.2.2 基于飞行经验的知识库建立
在当前的机动决策方法中,少有对飞行员空战战术知识的利用,这也导致机动决策的结果不能被飞行员所认可和解释,对此,通过对公开的战术书籍和项目学习以及和与飞行员现场交流,建立基于飞行员空战战术知识的知识库,在当前空战态势满足If-Then规则时,输出将要采取的机动动作。
(1) 输入输出变量确定
专家系统2的输入变量为模糊化后得到的速度差、航迹倾角差、高度差和模糊空间方位,即:IL={LR、Lv、Lγ、Lh、LW},其中LR、Lv、Lγ、Lh的模糊语言为[S、M、L],分别表示输入的小、中、大,LW的模糊语言为[1,2,3,4,5,6,7,8,9],分别表示我机相对敌机所处的空间方位序号。
输出变量为OL={DZ},DZ为机动决策得到的机动动作,模糊语言为[1,2,3,4,5,6,7,8,9,10,11],分别代表所选机动动作序号。
(2) 典型战术知识获取
典型空战战术描述:盘旋爬升俯冲反击。
使用时机:我机处于能量优势,追击机处于角度优势,双方距离较近。
基本方法:在初始处于角度劣势时,将己方能量优势转化为高度优势,采取盘旋爬升的方式(时刻1),当盘旋到比较陡直的时候,追击机的角度增加速度缓慢,爬升角也稳定下来(时刻2),此时采取跃升的方式,而追击机可以调整航迹偏角和滚转角,使我机处于其前上方(时刻3),如果此时追击机仍然使它的机头向上并持续转弯,我机可继续爬升以取得最大限度的高度优势,并尽可能减小过载,到达跃升顶端时,机头向下俯冲,直接指向目标并开火射击(时刻4)。如图5所示。
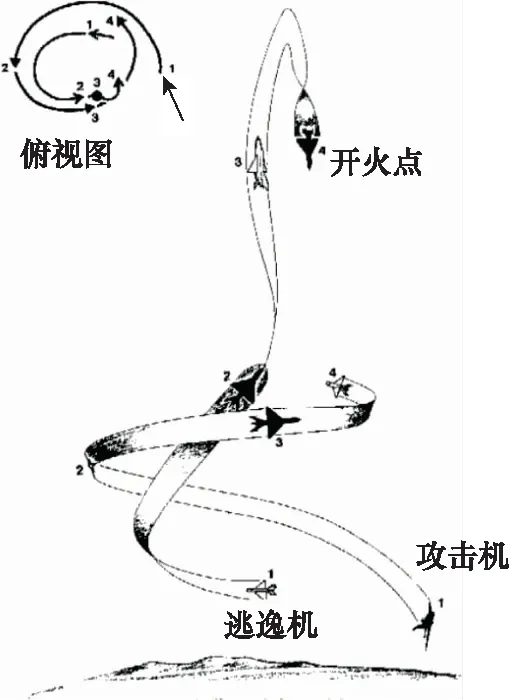
图5 典型空战战术图
If-Then规则获取如表2所示。

表2 If-Then规则获取表
通过对典型战术知识的规则提取,即可建立完备的专家系统。
3 基于DSC-JADE算法的机动决策
带边界约束的优化问题在现实世界是非常普遍的,在文献[26]中指出其普遍形式如下所示:
(),=(,,…,)

(12)

3.1 原始标准算法
初始化。和其余群智能优化算法一样,首先初始化种群:

(13)
式中:,,0是第0代第个个体的第个元素,=1,2,…,NP,=1,2,…,,NP为初始种群数,为变量的维度。
变异操作。对于种群中每个个体,差分进化算法的变异向量的产生方法表示为DE。其中,表示当前被变异的向量是随机的还是最优的,表示差向量的个数。
DE/rand1:,+1=1,+(2,-3,)
(14)
式中:1、2和3在种群中随机选择且1≠2≠3;缩放因子用于控制偏差的放大作用,且0≤≤2。
除此之外,偏差向量还可以由其他的方式产生。
DE/best1:,+1=best,+(1,-2,)
DE/current-to-best/1:
,+1=,+(best,-,)+(1,-2,)
DE/best2:,+1=best,+(1,-2,+3,-4,)
DE/rand/2:,+1=5,+(1,-2,+3,-4,)
(15)
交叉操作:交叉因子CR用于控制交叉概率。

(16)
选择操作。差分进化算法按照贪婪策略,从实验种群中选择个体作为下一代种群中的个体,具体的选择方式为

(17)
3.2 双策略竞争的JADE算法
JADE算法是2009年由Zhang等提出的一种DE算法的变体,近年来优秀的算法都是以JADE为基础改进的,其相对于原始DE算法的优势如下:
(1) JADE算法最大的优势在于通过使用可选的外部存档实施新的变异策略DE/current-to-pbest,外部存档利用历史数据提供进度方向信息。
无外部存档的变异策略:
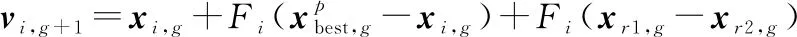
(18)
有外部存档的变异策略:
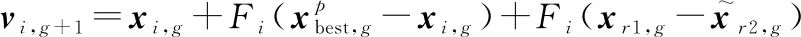
(19)

为平衡初期算法的全局搜索能力,本文加入另一变异策略进行竞争:

(20)
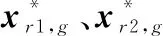
在文献[29]中提出了策略竞争的机制,初始时刻策略选择的概率和概率相同,之后根据策略是否成功来更新选择概率,交叉后生成的个体比原个体更优即为策略成功。

(21)
式中:为策略1成功次数;为策略2成功次数;为正常数,防止选择概率的显著变化。为避免搜索过程退化,若这两个选择概率低于阈值,则重置为初始值。
(2) 以自适应方式更新控制参数,CR来提高优化性能。
CR根据均值为,标准差为01的正态分布产生,根据均值为,标准差为01的柯西分布产生。初始设置为05,初始也设置为05。
将每一代成功的个体的CR值存储起来,即为,同样的将每一代成功的个体的值存储起来,即为。
在每一次迭代后,更新和的值为
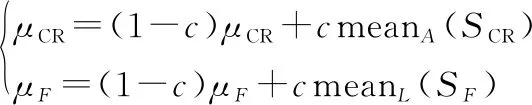
(22)
式中:是权值,设置为0.5;mean指计算算术平均数。mean的定义如下:
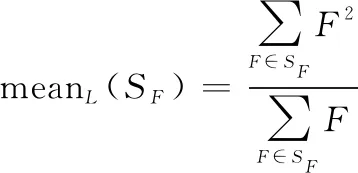
(23)
DSC-JADE伪代码如算法1所示。

算法 1DSC-JADE算法伪码1.Begin2.μCR=0.5,μF=0.5,A=⌀,q1=0.5,q2=0.53. 初始化种群4. While G≤Gmax do5. SCR=⌀,SF=⌀6. for i=1 to NP do7. CRi=rand ni(μCR,0.1),Fi=rand ci(μF,0.1)8. 根据q1,q2的值选择变异策略生成vi,g+19. for j=1 to D do

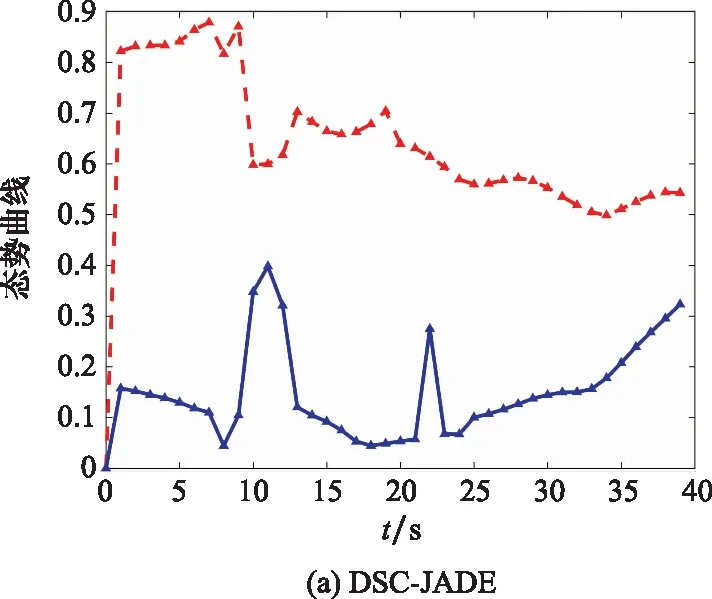
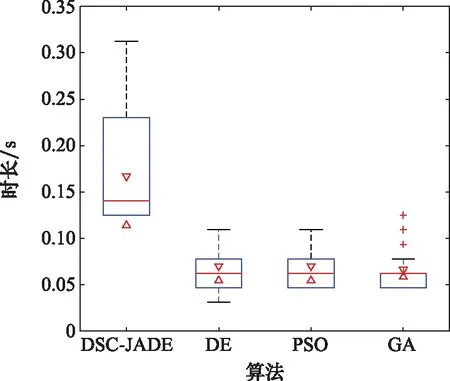
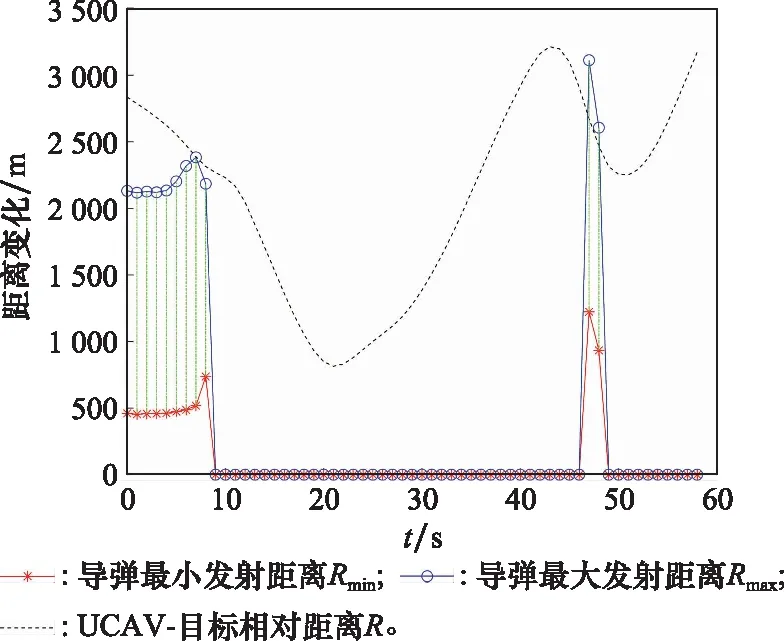
10. if rand [Δmax,Δmax,Δmax]=[5°,30°,05] [Δmin,Δmin,Δmin]=[-5°,-30°,-05] 双方控制量限制范围为 [,,]=[34°,180°,1] [,,]=[-15°,-180°,015] 我机与追击机初始控制量都是[,,]=[0,0,05],仿真每步时长设置为1 s,追击机采用文献[30]中的试探机动决策的方法,由于本文篇幅原因,在此不加以赘述。 本文建立的机动决策框如图6所示。 图6 基于模糊专家系统与DSC-JADE算法相结合的UCAV逃逸机动决策框图 为验证采用的DSC-JADE算法在求解控制量变化率问题上的实时性,以时刻机动对抗双方状态为条件,对专家系统决策后输出的机动动作对应的控制量变化率范围为寻优范围,进行寻优比较,寻找使得目标函数值最大的控制量变化率,并与蚁群算法(ant colony optimization, ACO), 粒子群优化(particle swarm optimization, PSO)算法、遗传算法(genetic algorithm, GA)、DE等算法进行性能比较,最大迭代次数都为50,种群规模NP都为100,其余各算法参数设置如表3所示,仿真步长为40,得到40次寻优算法所用时间以及双方机动轨迹和态势曲线如图7和图8所示。 表3 算法参数设置表 图7 采用DSC-JADE算法机动决策双方机动轨迹图 图8 采用DES-JADE、DE、PSO、GA算法得到的双方总体态势变化曲线 ACO中,为信息素的相对重要程度,为启发式因子的相对重要程度,为信息素挥发系数;PSO中,为粒子的个体学习因子,为粒子的社会学习因子,为惯性因子;GA中,为交叉概率,为变异概率。 从仿真结果(见图9)来看,经过40个步长的仿真,采用DSC-JADE算法的UCAV最终态势值相较于其余算法最大,为0.323 1,比较来看DSC-JADE算法明显具备更好的寻优性能。从算法使用时间来看,DSC-JADE算法每步寻优所用时间中位数为0.141 2 s;相较于其余算法寻优所用时间略长,但相较于1 s的决策周期而言是可接受的,且能更好地寻找到全局最优点,避免陷入局部最优。 图9 算法所用时长箱线图 为体现所建立专家系统的有效性,将逃逸机采用专家系统其逃逸机不采用专家系统进行对比,为体现一般性,进行100次蒙特卡罗仿真,对比优胜率,同时文中各选取其中一组具有代表性的仿真实验进行描述。 仿真终止条件:由于真实近距空战对抗训练中,对于追击科目而言,通常会设置时间限制,因此设定时间大于60 s时仿真终止,宣布逃逸机逃逸成功;若攻击机连续3 s位于导弹攻击区内,判定UCAV被攻击机发射的红外空空导弹击中,宣布追击机胜利;设定空战区域高度大于1 000 m,飞行高度小于1 000 m时超出空战范围,仿真结束。 (1) 包含决策过程的追击机对抗不含专家系统的UCAV如图10~图12所示。 图10 包含决策过程的追击机对抗不含专家系统的UCAV机动轨迹图 图11 追击机对抗不含专家系统的UCAV双方总体态势变化曲线 图12 追击机与不含专家系统相对距离和导弹可发射距离变化曲线 可以看到,当UCAV不采用专家系统时,其决策出的机动为爬升机动,但由于寻优范围过大,容易陷入局部最优,导致没有采用最大过载进行爬升,在21~24 s时在追击机导弹发射区域内,导致被追击机击中。 (2) 包含决策过程的追击机对抗含专家系统的UCAV如图13~图15所示。 图13 包含决策过程的追击机对抗含专家系统的UCAV机动轨迹图 图14 追击机对抗含专家系统的UCAV双方总体态势变化曲线 图15 追击机与含专家系统的UCAV相对距离和导弹可发射距离变化曲线 从图13~图15中可以看出,UCAV一开始采用专家系统决策得到的机动动作也是爬升机动,但由于其寻优范围较小,寻优得到的过载值更大,因此在第8 s时躲过了追击机导弹锁定,并在之后决策得到右侧俯冲、俯冲、左侧俯冲、爬升等一系列机动动作,使得UCAV形成较优的态势,经过60 s,追击机没有击中UCAV,UCAV完成逃逸。 图16中,从每步决策所用时长的数据来看,不采用专家系统限制寻优范围,每步时长决策平均值为0.275 1 s,标准差为0.078 4;采用专家系统限制寻优范围,每步决策时长平均值为0.168 4 s,标准差为0.059 8。从表4结果来看,采用专家系统,平均每步决策时长减少约33.4%,且稳定性更好。 图16 采用专家系统与不采用专家系统每步决策所用时长变化曲线 表4 100次蒙特卡罗空战仿真实验结果统计 本文针对UCAV处于不利态势时的逃逸机动决策问题,将DSC-JADE算法引入模糊专家系统进行逃逸机动决策,建立了基于滚动时域的控制量变化率寻优的机动决策模型,相较而言更为贴近UCAV的真实控制,且改进算法相对其余群智能算法能迅速完成控制量变化率寻优,在全局最优的搜索能力上有所提升;为将空战知识运用到机动逃逸中去,将寻优范围运用专家系统进行限制,以达到想要的机动动作,并大大提高决策的实时性。最后仿真结果显示用专家系统决策实时性提升约33.4%,逃逸成功率提升29%,且得到的机动轨迹更符合战术知识。4 仿真分析

4.1 算法的性能比较


4.2 对比实验

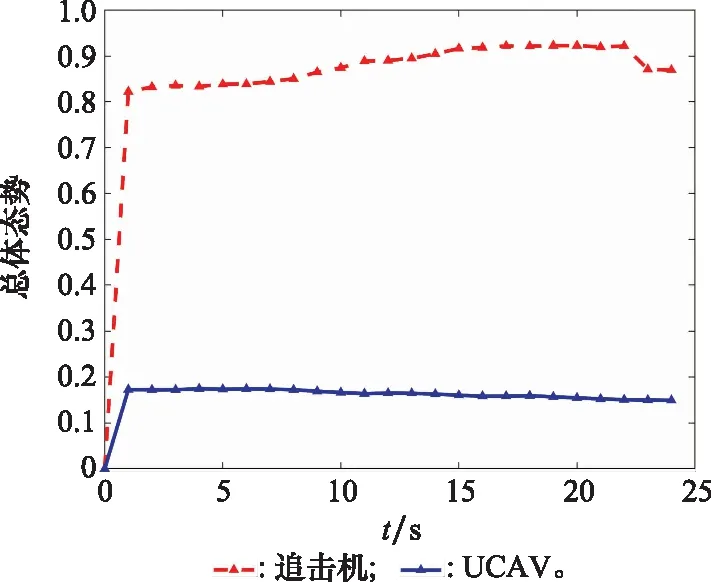
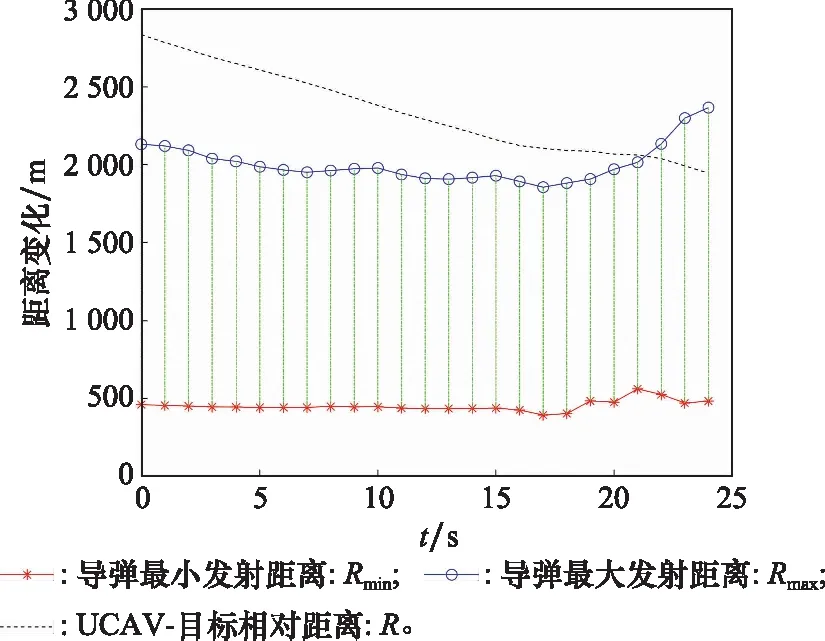
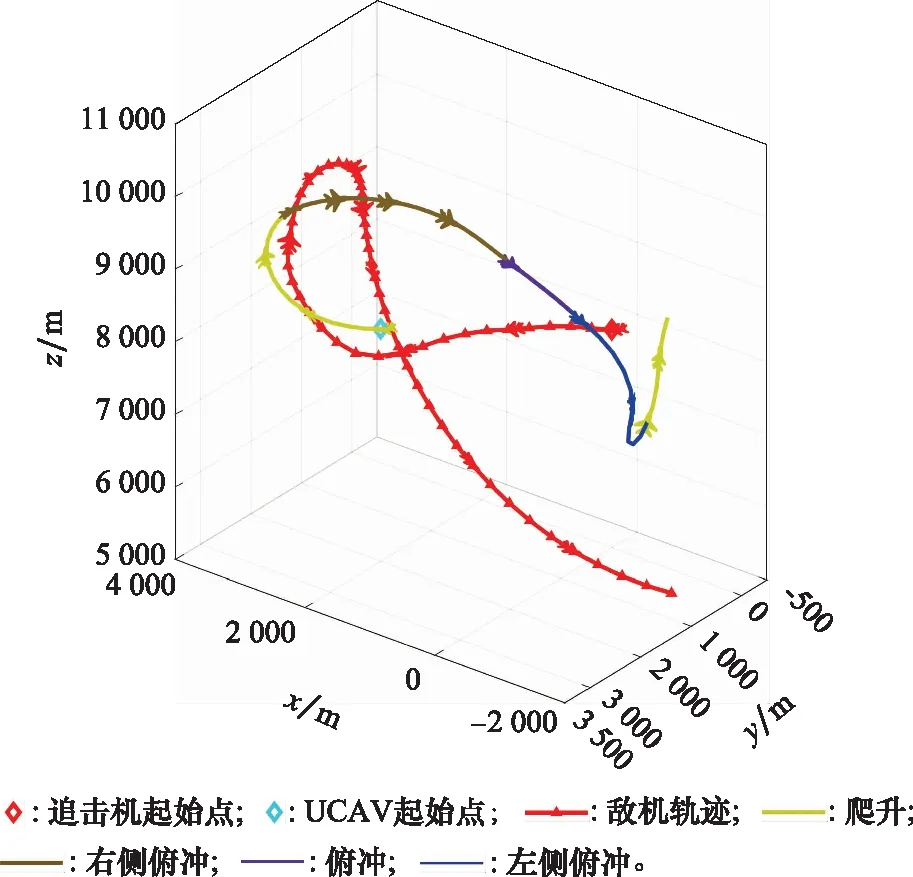



5 结 论
