基于灰关联分析和时空偏好特征的兴趣点推荐算法

陈江美, 张文德

(1. 福州大学经济与管理学院, 福建 福州 350108; 2. 福州大学信息管理研究所, 福建 福州 350108)

0 引 言

随着移动社交网络的普及与应用,多样化的位置签到及共享功能不断涌现,获取用户的地理信息更为容易,助推了基于位置的社交网络(location-based social network,LBSN)的兴起。例如,目前较为流行的Gowalla、Yelp、Foursquare等移动平台不仅具备社交功能,还为用户提供了诸多与位置有关的服务。LBSN中主要包含了用户与位置属性、社交关系及签到时间等信息,用户可通过“签到”的方式分享其可能喜欢的地点,从而衍生出多样化的位置服务功能。其中,兴趣点(point-of-interest,POI)推荐作为一项重要的服务内容,近年来受到了学者的广泛关注。POI是指用户签到的地点,如景点、电影院等,兴趣点推荐能够有效缓解位置过载问题,从而提升用户在LBSN中的个性化体验,并有助于商家挖掘潜在客户,成为了当前研究的热点问题。

目前,国内外学者对 POI推荐工作已开展大量的研究,并设计不同的推荐策略来改善推荐性能,但仍存在一些局限。首先,用户的偏好存在漂移性,即用户的兴趣可能随时间在动态变化,虽然少数研究将时间纳入POI推荐工作,但性能有待提高。LBSN中的用户签到矩阵十分稀疏,而当前纳入时间的研究主要是利用时间间隙来划分矩阵,加剧了评分矩阵的数据稀疏性。因此,如何合理地挖掘用户的时间偏好是重点。其次,用户的移动行为符合个性化特征,但多数的研究认为用户的地理行为偏向于统一的分布,未充分考虑用户个性化特征,如何更好地实现地理行为的个性化值得研究。最后,LBSN存在海量的异构数据,这些异构数据对推荐结果有着不同程度的影响,如何有效地融合多类型异构数据增加了推荐的难度。

在传统POI推荐工作的基础上,本文针对上述问题,提出了一种基于灰关联分析和时空偏好(grey relational analysis and temporal-spatial information, GRA-TS)的POI推荐算法。本文的贡献主要有以下3点:

(1) 考虑用户偏好动态变化和数据稀疏性问题,提出将时间融入矩阵分解算法中,以刻画用户对POI的时间偏好。同时,将灰色系统理论沿用于此,利用灰关联分析方法度量各时间段的相似度,从而减弱数据稀疏的影响,有效改善推荐性能。

(2) 考虑用户的签到分布符合个性化特征,采用自适应核密度估计方法来模拟用户的空间偏好,从而捕捉用户的空间偏好。

(3) 综合考虑用户的时间偏好和空间偏好特征,通过模拟用户的时空偏好行为,获得用户的综合偏好分数。同时,将本文提出的算法进行数据实验,结果表明了该算法相较于其他基准算法具有更优的推荐性能。

1 研究综述

基于位置的社交网络中蕴含着丰富的信息,目前POI推荐的相关研究主要通过融合上下文信息(如地理信息、时间信息),采用协同过滤算法、矩阵分解算法、深度学习、谱聚类等方法模拟用户的决策行为。在已有的研究中,考虑用户对地理距离较敏感的特性,Ye等人采用幂律分布建模用户的地理行为偏好,将地理信息融入基于用户的协同过滤算法中。但交互矩阵十分稀疏,协同过滤方法难以发挥作用。考虑矩阵分解算法能缓解稀疏问题,文献[6-7]将地理信息纳入加权矩阵分解算法的框架中以挖掘用户的偏好。Zhang等人则考虑用户潜在的地理和社交信息,通过矩阵分解算法联合求解用户的综合偏好。为了进一步挖掘用户的地理行为偏好,文献[9-11]将地理因素结合多种情景信息来模拟用户的签到行为,进而提高推荐质量。

近年来,一些学者在试图改善推荐性能时,将用户签到的时间作为重要的情景信息融入推荐工作中。为了模拟用户的时间偏好,学者们从多个角度进行建模。Yin等人利用协同过滤技术为目标用户在给定时间推荐地点。但协同过滤技术易受稀疏影响,推荐效果不佳。Gao等人将时间所具有的非统一性和连续性嵌入矩阵分解算法中。但由于考虑要素单一,无法全面挖掘用户的偏好。Rahmani等人考虑用户的周期性行为,将时空信息纳入矩阵分解框架中。文献[15]融合空间、社交和时间信息的影响,探究各要素在POI推荐工作中的作用。上述算法虽考虑了时间影响,但主要利用时间划分签到矩阵,造成原本就稀疏的矩阵更加稀疏,导致动态推荐效果不佳。

综上可知,目前大量的基于时空的研究成果仍存在局限性。传统动态推荐的工作鲜少考虑时间特征的影响,造成对用户的时间偏好挖掘不充分,同时忽略了时间戳细化用户签到矩阵后带来的稀疏性影响。另外,上述的工作主要将用户的地理行为建模为统一的距离分布,忽略了用户的个性化行为。为此,本文提出了一种新的基于时空偏好的POI算法,以提高用户的动态个性化推荐效果。

2 灰关联分析方法

灰色系统理论是一种能处理贫信息问题的方法。灰关联分析是灰色系统理论中一种重要的研究方法,通过判断序列曲线几何形状的相近程度以衡量序列间的相似性,对样本数据量及数据的分布规律无特殊要求,可有效处理复杂贫信息系统的数据。因此,本文将灰关联分析理论运用到推荐系统领域中,用来度量数据稀疏条件下的相似度。

2.1 灰关联度

灰关联系数:设={()|∈}为参考序列,={()|∈}为对应的比较序列,={1,2,…,},={1, 2,…,},称

((),())=

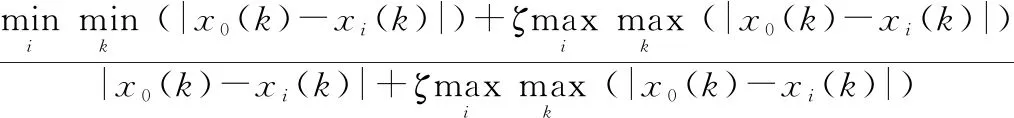
(1)

为参考序列和比较序列在处的灰关联系数。其中,为分辨系数,一般取05。

灰关联度:设存在((),())为非负数,为度量参考序列和比较序列的相似度,称

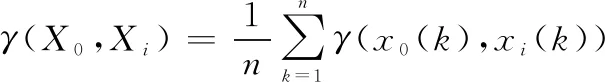
(2)

为第个比较序列的灰关联度。

2.2 灰关联熵与熵关联度

灰关联密度:由定义1可知,((),())为参考序列和比较序列在处的灰关联系数,称

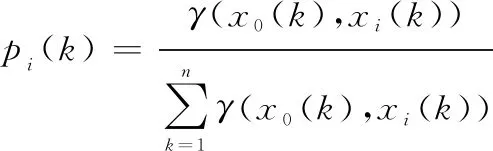
(3)

为第个比较序列在处的灰关联密度。

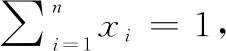
(4)

为第个比较序列的灰关联熵。

熵关联度:设表示第个比较序列的灰关联系数,称

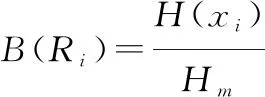
(5)

为第个比较序列的熵关联度。其中，=ln,表示最大熵。

2.3 均衡接近度

传统的灰关联分析方法存在局部异常点的倾向及信息损失的局限,为了克服此缺陷,在灰关联分析方法中引入灰关联熵,利用均衡接近度作为衡量向量之间相似度的标准。

均衡接近度:由灰关联度和熵关联度组合乘积,得

(,)=(,)·()

(6)

式中：(,)表示参考序列和比较序列的均衡接近度。

均衡接近度方法由传统的灰关联分析方法发展而来,灰色系统理论中灰关联度的概念可用于描述向量间的相似性。近年来,相关学者将灰关联分析方法拓展到推荐领域。文献[25]指出传统的相似性度量方法面临数据稀疏性和相关性两大挑战,结合灰关联分析方法提出一种新的协同过滤预测模型。文献[26-27]利用灰关联分析挖掘数据的关联性,进而探索用户间的关系。文献[28]将灰色系统理论应用到社交推荐中,通过优化预测模型,以缓解数据稀疏性和差异性。本文沿用这一思路,将灰色系统理论引入POI推荐领域,并将均衡接近度的概念用到时间相似度之上,以改进传统的余弦相似度方法存在局部异常点的不足,进而提高相似度计算的准确性,改善数据稀疏问题。

3 GRA-TS推荐算法

3.1 算法框架及思想

本文从时间和空间的角度出发,设计出统一的POI推荐算法框架,如图1所示。本算法主要思想是将用户签到的时间特征细化,分解带有时间戳的用户评分矩阵,利用处理小样本的灰关联分析方法度量时间相似度,进而降低稀疏性的影响。同时,运用自适应核密度估计方法个性化地建模用户的空间偏好。最终,提出了一种GRA-TS算法,在第32～第34节将给出详细的模型描述。

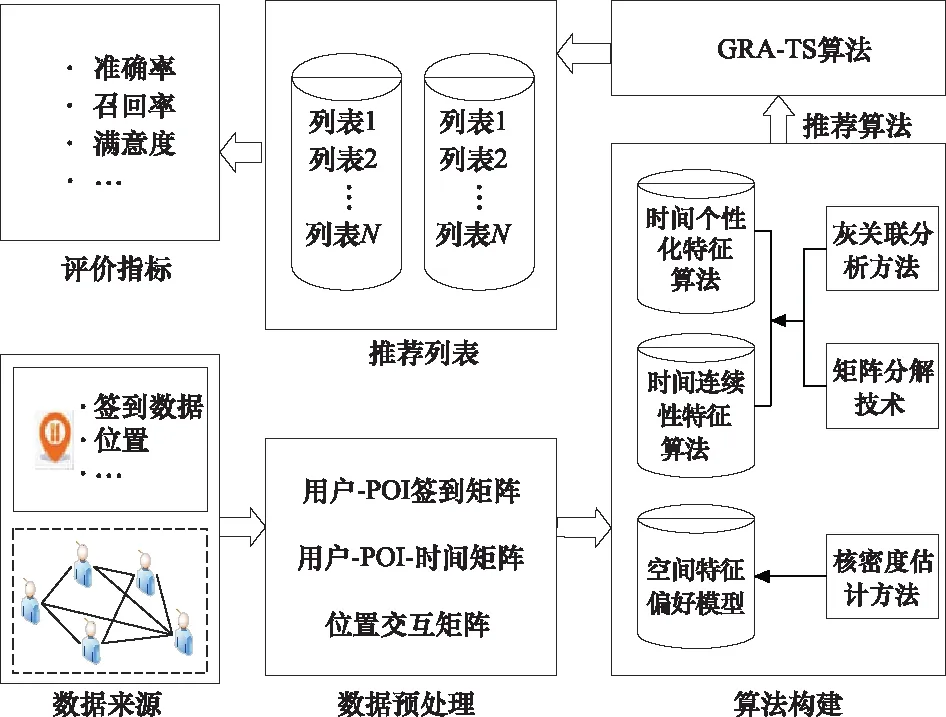
图1 GRA-TS算法的框架结构图

3.2 引入时间特征的矩阵分解算法

与协同过滤算法建模时间偏好相比,矩阵分解算法具有更好的可扩展性与缓解稀疏性的能力。鉴于用户的签到行为受时间影响,本节将时间的个性化和连续性特征融入矩阵分解算法框架中,结合灰关联分析方法,以描述用户对POI的时间偏好。

321 时间个性化特征建模

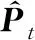
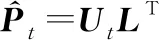
(7)

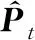
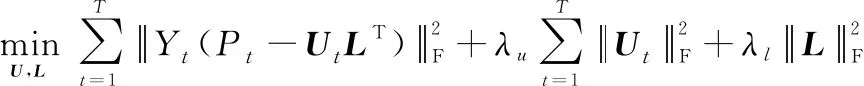
(8)

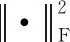
322 时间连续性特征建模

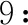
(9)

式中：(,-1)表示时间段和-1的相似度;()表示用户在时间间隔内的签到偏好。为了简化损失函数,当=1时,令=-1,则-1=,将其转化为矩阵形式如下:

(10)

式中：表示个用户间的对角时间系数矩阵,表达式如下:

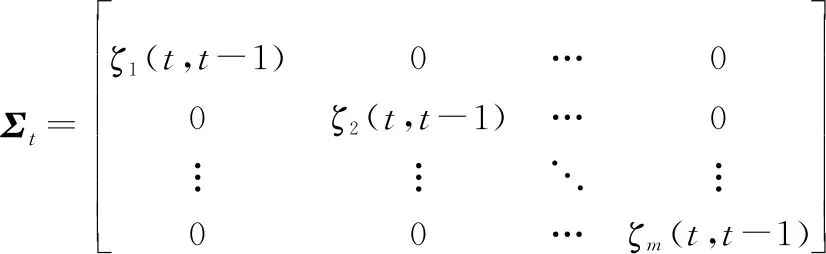
(11)

323 灰关联分析度量相似度

灰关联分析方法可用于衡量向量间的关联程度,借助灰色理论中“接近度”的思想,利用均衡接近度方法计算用户签到POI各时间段间的相似度。因此,利用式(6)均衡接近度方法对式(9)中的时间相似度进行求解如下:

(,-1)=(,-1)

(12)

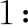
324 统一的时间偏好特征

本节综合考虑上述时间个性化和连续性特征,并建立统一的时间偏好函数。由于式(8)和式(10)中的同为用户特征偏好矩阵,若单独对两个优化函数求解很难满足统一性要求。鉴于此,本节将两个矩阵分解的优化函数联合求解如下:

(13)

式中:为调整时间正则化的参数。

本文利用变更最小二乘法(alternative least square, ALS)对目标函数进行优化,当求解一个隐特征向量时,固定其他变量。其中矩阵和为待求解参数,训练过程中其更新公式如下:

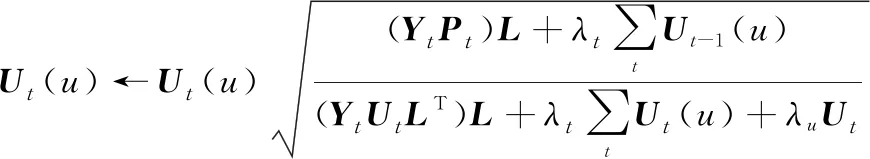
(14)

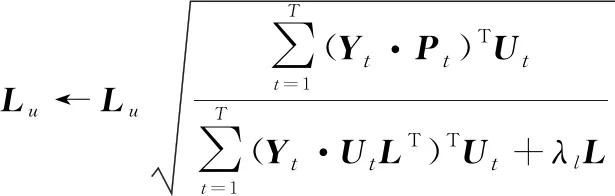
(15)

通过优化式(14)和式(15),可求解参数矩阵和,并将其代入式(7)计算得到预测矩阵中的各元素值, 将其定义为用户的时间偏好特征预测值。

3.3 引入空间信息的个性化推荐算法

用户的空间偏好通常指用户的决策受地理位置信息的影响程度,考虑地理位置对用户的签到行为具有重要作用,本文利用自适应核密度估计方法来建模用户的空间偏好,以实现个性化推荐。设={,,…,}表示用户已签到POI集合,其中∈,(,)表示POI的经纬度坐标。同时,考虑用户的空间偏好特征,利用核密度估计方法捕捉用户的地理偏好,并将高斯分布作为核函数,获得用户对未签到POI的预测函数为

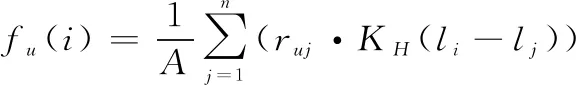
(16)

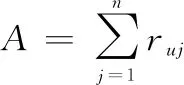
(17)

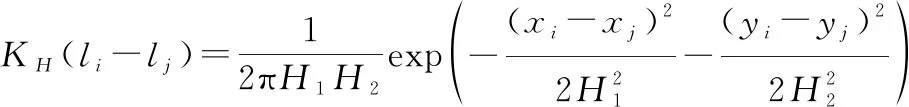
(18)

式中:表示用户签到POI的总次数;表示用户对POI的访问次数;(-)表示包含两个全局固定带宽(,)的核函数。(,)的公式如下:

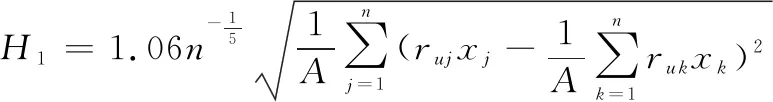
(19)

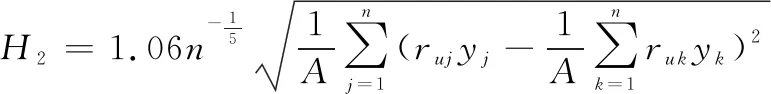
(20)

为实现个性化推荐,本文并非直接利用式(16)的()值来描述用户的空间偏好,而是用来决策每个被签到POI的自适应带宽:

=(())-

(21)

式中:表示敏感参数,值越大意味着对()越敏感;表示几何平均数,的表达式如下:

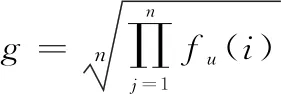
(22)

最终,根据式(19)和式(20)的固定带宽值(,)和式(21)的自适应带宽值,预测用户在未签到POI上的自适应核估计的推荐概率分布如下:

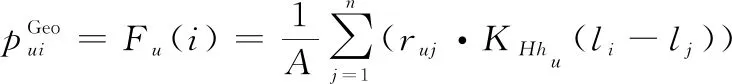
(23)

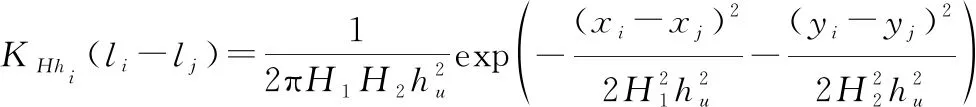
(24)

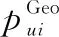
3.4 融合时空特征的算法优化

(25)

因此,将式(25)与式(23)中度量用户的空间偏好的算法相结合,建立最终的统一优化算法GRA-TS,获得用户未签到POI的最终预测偏好如下:

(26)

4 数据实验与分析

4.1 数据集介绍

本文实验的数据集来自Foursquare网站,该网站是一个基于用户地理位置的社交网站,采用其发布的真实公开的Foursquare数据集来评估所提算法的性能,其包含的具体内容如表1所示。

表1 数据集统计

为了评估算法的精度,先进行数据预处理,过滤掉一些发生次数较少的异常数据,分别删除访问频率少于10个POI的用户和被访问频率少于10个用户的POI。

4.2 度量指标

为了验证本文算法的有效性,将实验中用户签到数据按8∶2的比例随机分成训练集和测试集。根据top-的推荐排序,为每个用户推荐得分最高的前个POI,并对生成的POI推荐列表进行评估。本文主要是对算法的基本性能作对比,重点是找出通过训练算法生成的POI列表总数中有多少是目标用户在测试集中实际签到的POI。准确率precision@与召回率recall@是top-推荐中的两个基本指标。为此,在对比实验部分采用这两个基本指标进行算法的评估,公式如下:

(27)

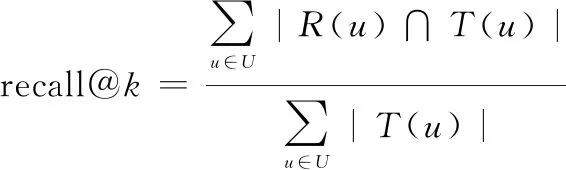
(28)

式中:()表示训练集通过本文算法训练生成的POI推荐列表;()表示测试集中用户对POI的签到列表。

4.3 实验对比与算法评估

为了评估算法的性能,选取了5种基准算法与本文提出的GRA-TS算法进行比较。

(1) LRT算法:基于时间效应的POI推荐算法,考虑时间非统一性和连续性两大特征,将其分别纳入矩阵分解算法,综合求解获得用户的最终偏好。

(2) SCGT算法：融合社交、分类、地理与时间信息的POI推荐算法利用固定带宽的核密度估计捕捉用户的地理偏好,并结合社交信息提出统一的推荐模型。

(3) iGSLR：融合地理与社交影响的位置推荐算法，采用固定带宽的核密度估计方法模拟用户的地理行为,利用协同过滤建模用户的社会影响力,通过融合获得最终的用户偏好。

(4) PRUG：基于用户兴趣和地理因素的POI推荐算法，利用自适应核密度估计与朴素贝叶斯算法捕捉用户的空间偏好,结合用户的偏好生成统一的模型。

(5) STACP：基于时空偏好的POI推荐算法，考虑用户签到行为的周期性,利用矩阵分解框架建模时空信息的影响,求解获得用户的潜在偏好。

其中,LRT与STACP是两种基于时间因素的算法,可有效地研究动态推荐的效果。而SCGT、iGSLR、PRUG及STACP分别采用了不同的地理建模方式来挖掘用户的偏好,有利于充分探究个性化推荐问题。同时,这些算法结合了一种或多种情景信息,有助于研究时空信息对推荐工作的影响,进而验证本文算法的有效性。因此,将上述5种算法作为本文的对比方法。

在实验的参数设置部分,依据文献[13]中的最优参数的选取,将本文算法中的正则化参数、和分别设置为2,2,1,经过实验测试适用于本文的算法,并应用于以下实验。对敏感参数,通常将值取为0.5,经验证此时用户的地理偏好得分最佳。

4.3.1 相似度优化对推荐性能影响

为了探究灰关联分析方法度量时间相似度对推荐结果的影响,本节将基于GRA的时间影响模型(GRA-temporal, GRAT)算法与基准算法LRT进行对比。其中,GRAT是本文算法的一部分,主要利用矩阵分解算法描述时间的个性化和连续性特征,与LRT相比,GRAT算法采用均衡接近度方法刻画时间段间的相关性,而非运用传统的余弦相似度度量方法。

本实验选取为5、8、10、12、15和20,分别对比两种算法在Foursquare数据集上的推荐精度和召回率的变化情况,并将实验中的参数设为最优值。从图2(a)和图2(b)看出,GRA算法的推荐准确率和召回率相较于LRT有显著的提高,表明了均衡接近度方法在度量时间相似度方面较余弦相似度方法具有更突出的效果,说明了本文相似度优化的有效性。灰关联分析方法能改善推荐性能的原因归结两点:① 传统的相似度方法易遭受局部异常点影响,造成数据损失而影响推荐质量,而均衡接近度方法可以减弱局部异常点的影响;② 均衡接近度方法能处理贫信息问题,本算法利用时间划分矩阵造成了严重的稀疏问题,将灰关联分析方法沿用于此,并采用矩阵分解算法能有效改善数据稀疏性。因此,实验结果表明了利用均衡接近度来计算相似度能改善推荐性能。

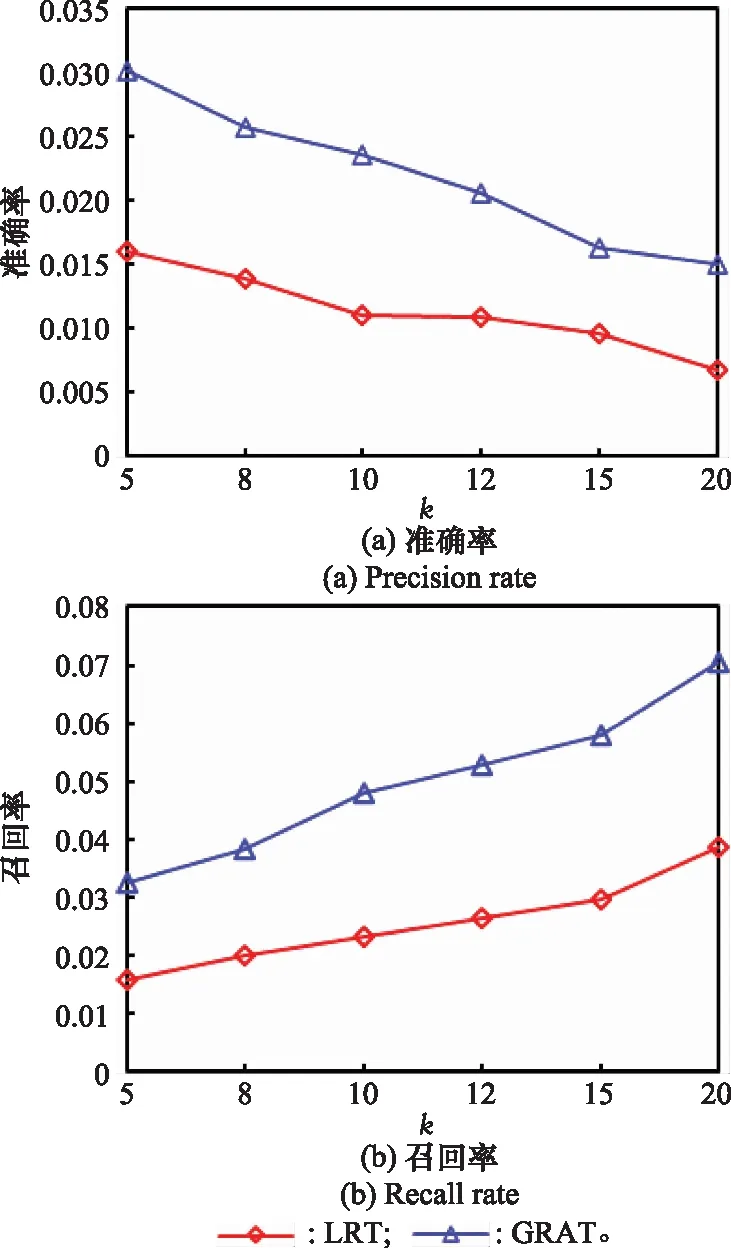
图2 相似度优化前后的推荐准确率和召回率

4.3.2 地理因素影响

为了研究基于幂律分布的地理因素在预测用户偏好上的影响,同时探究采用自适应核密度估计方法捕捉用户地理偏好的有效性,将本文提出的GRA-TS算法与GRAT算法、基于灰关联分析与幂律分布(grey relational analysis-power law distribution, GRAP)的算法进行对比。其中,GRAT算法是本文算法的一部分,与GRA-TS算法相比,此算法未考虑地理因素的影响。GRAP则利用幂律分布来模拟地理行为影响。实验比较为5、8、10、12、15和20时,3种算法在数据集上的准确率和召回率变化情况,如图3所示。

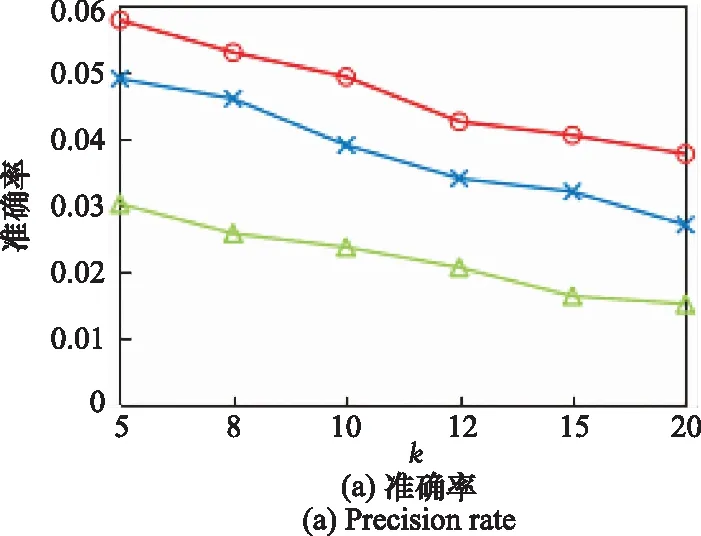
图3 融合不同地理信息的算法性能对比

由图3看出,未考虑地理因素的GRAT算法的推荐准确率和召回率低于其他两种算法,说明地理信息在本文的推荐工作中具有重要意义,是影响推荐策略的主要因素之一。GRAP算法与本文所提的算法相比,显然看出GRA-TS算法的推荐性能更优。GRAP利用幂律分布捕捉用户的地理偏好,性能优于GRAT算法,但其将用户的移动行为视作统一的分布,忽视了用户个性化行为的影响。GRA-TS算法利用自适应核密度估计方法描述用户个性化的签到行为,表现出最好的推荐性能,说明了本文对地理建模的合理性。

4.3.3 算法的性能对比与分析

在Foursquare数据集的基础上,将本文算法的参数设定为=2、=2和=1时推荐性能最佳,并根据其他5种文献设置的参数值,使各算法的推荐效果最优。实验将6种算法进行比较,对比结果如图4所示,其描述了各算法在POI推荐列表长度为5、8、10、12、15和20时的推荐性能。从图4看出,本文提出的GRA-TS算法的性能最优。同时,值的增加有易于用户挖掘更多的POI,因此各算法的推荐准确率在逐渐降低与召回率在逐渐升高。由图4(a)和图4(b)可见,GRA-TS算法的推荐准确率和召回率在相同条件下均优于其他5种算法,特别相较于LRT的性能有显著提升。考虑LRT只纳入时间信息,且算法遭受严重的数据稀疏问题,因此推荐的性能最低。SCGT与iGSLR采用固定带宽的核密度估计函数建模地理影响,并融合社会影响力,初步考虑了不同用户的地理行为偏好,但两种算法易受到数据稀疏影响。STPACP将用户的时空偏好嵌入矩阵分解框架,与SCGT与iGSLR相比,矩阵分解分解算法能缓解稀疏问题,但未充分挖掘用户签到的时间特征,性能有待提高。PRUG融合了核密度估计和朴素贝叶斯算法描述用户的地理偏好,结合了用户偏好影响,性能优于上述4种算法,但未考虑用户的动态偏好,结果次优。与上述5种算法对比,本文提出的GRA-TS算法考虑了时间的个性化和连续性特征,进而描述用户的时间偏好,并运用灰关联分析度量时间相关性,缓解了数据稀疏的影响,提高了动态推荐效果。同时,利用自适应核密度估计方法捕捉用户的移动行为偏好,有效地实现个性化推荐,增强了推荐的时空特征关联。综上,GRA-TS算法的推荐性能最佳,表现出最好的推荐性能。

图4 6种算法在Foursquare上的推荐性能

5 结 论

为了提高动态推荐与个性化推荐的效果,本文提出了一种基于GRA-TS的POI推荐算法。该算法将用户签到的时间特征细化,把灰关联分析与矩阵分解算法相结合,利用灰关联分析计算时间相似度,减少了数据稀疏的影响,有效地提高了动态推荐的效果,为应对推荐系统的稀疏性问题提供了新的方法。还采用了自适应核密度估计建模用户的地理行为,增强了个性化体验。实验结果表明,本文提出的算法在推荐准确率和召回率方面均优于其他基准的推荐算法。在未来的工作中,将进一步挖掘更多的情景信息来提高推荐性能。同时,将异地问题作为突破重点,进一步深入完善模型。