基于短波通信的OTFS波形应用研究

武晓静，肖 悦

(电子科技大学 通信抗干扰技术国家级重点实验室，四川 成都 611731)

0 引言

短波通信[1-2]使用3～30 MHz频段的电磁波调制信息，经过电离层反射到达接收端，从而不受中继制约，抗毁性强，可应用于各种远距离通信场景。因而，很多国家将其列为应急、军事领域的重要通信手段。以美国为例，在陆空联络、舰队编组以及特种作战中大量应用短波通信，并提出一系列标准和体制[3-4]，在世界范围内得到广泛关注和研究。

短波通信可支持单载波和多载波体制[5]，其中单载波具有较低的峰均功率比，接收端在时/频域结合均衡算法以对抗多径衰落，在短波电台中得到广泛应用；多载波以正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)为代表，能够高效地对抗频率选择性衰落，且有利于融合多天线技术，提升短波通信的数据率和可靠性。另一方面，短波通信带宽受限，电离层受天气影响快速变化，信号将面临多普勒效应引起的频率扩展和载波间干扰(Inter-Carrier Interference，ICI)，影响传统单/多载波体制的检测性能，导致短波电台的传输能力下降。

近期，正交时频空(Orthogonal Time Frequency Space，OTFS)[6]以其对抗多普勒扩展的能力，成为面向6G[7]的候选波形，引起了学术界的广泛关注。OTFS变换使每个时延-多普勒(Delay-Doppler，DD)域的调制符号经历相近的衰落[8]，且被充分扩展到整个时频(Time-Frequency，TF)域，从而对抗衰落和干扰。同时，OTFS可沿用OFDM的结构，仅需在发射端添加预处理模块，从而与OFDM波形兼容，利于设备更新换代。

为了克服多普勒扩展对短波通信的影响，降低短波电台对多普勒效应的敏感性，本文首次将OTFS波形应用于短波通信，在TF域采用块最小均方误差(Block Minimum Mean Square Error，Block-MMSE)均衡[9]，达到和DD域MMSE均衡方法[10]一致的性能，并降低了系统的实现复杂度。通过计算机仿真，对于OTFS、OFDM和单载波波形的误比特率(BER)性能进行了验证，揭示了短波信道下OTFS波形的特征和优势，为新波形在短波通信中的应用提供了借鉴。

1 短波信道

当信号带宽有限且限于较短时间时，短波信道基本稳定，可以近似为静态模型。在现有研究中，Watterson提出的高斯散射增益抽头延迟线模型[11]能较好地模拟短波信道的特性且计算复杂度低，因此被广泛使用。国际电信联盟无线电通信组(ITU-R)[12]将该模型简化为由两个功率相同的独立衰落路径组成的模型，其中衰落过程的包络为瑞利分散式，即两条路径服从独立的瑞利分布。

在信号传输方面，单载波频域均衡(Single Carrier Frequency Domain Equalization，SC-FDE)和OFDM系统在发射端通过添加循环前缀(Cyclic Prefix，CP)将线性卷积转换为循环卷积以减轻码间干扰(Inter-Symbol Interference，ISI)，移除CP后的接收端时域信号可以表示为：

(1)

式中，L为信道抽头个数，M为FFT长度，〈·〉M表示对M求模，m=0,1,…,M-1，s(m)和r(m)是第m点处的时域发送和接收信号，w(m)表示该点处均值为0、方差为N0的加性高斯白噪声，h(m,l)是第l个抽头在第m点处的单位冲击响应。将式(1)表达为如下矩阵形式：

(2)

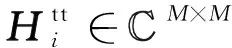
2 传统SC-FDE和OFDM系统

传统单载波频域均衡和多载波OFDM系统的原理框图如图1和图2所示。二者在结构上的主要区别是IFFT模块的位置。

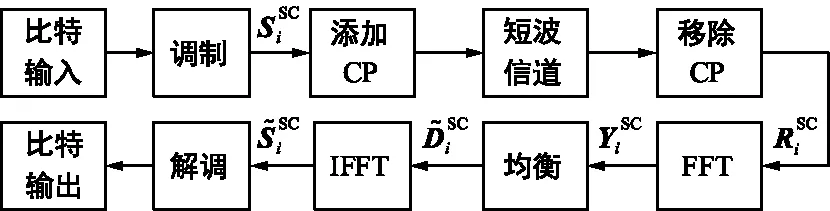
图1 传统SC-FDE系统框图Fig.1 Conventional SC-FDE system block diagram

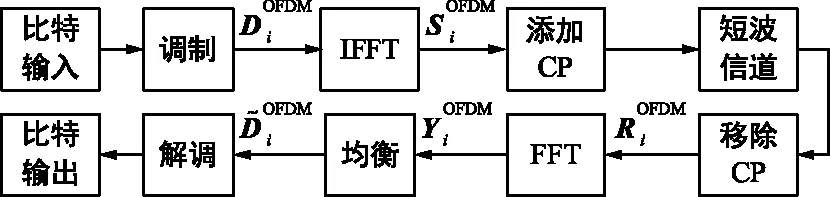
图2 传统OFDM系统框图Fig.2 Conventional OFDM system block diagram

两种系统在接收机均通过快速傅里叶变换(Fast Fourier Transform，FFT)将时域接收信号转换到频域以进行频域均衡。当脉冲响应不变时，不存在ICI，两系统FFT后得到的频域接收信号可写为：

Y(k)=g(k)D(k)+W(k),k=0,1，…,M-1，

(3)

SC-FDE体制利用MMSE进行一阶频域均衡：

(4)

OFDM体制则利用迫零(Zero Forcing，ZF)运算进行一阶频域均衡恢复频域的各点信号：

(5)

无论对于SC-FDE还是OFDM波形体制，多普勒效应会破坏子载波间的正交性，从而引入ICI，造成性能损失。

3 OTFS系统

OTFS波形信号在DD域内传输。发射机首先将待传输的星座符号映射到DD域，再通过逆辛傅里叶变换(Inverse Symplectic Finite Fourier Transform，ISFFT)将信号变换到TF域，最后利用海森堡变换(Heisenberg Transform)转到时域发送。接收机对应执行发射机的逆过程，信号从DD域到时域之间的转换使得每个DD域的数据符号具有与时间无关的相似衰落，从而减少衰落和干扰，获得更好的性能。

3.1 系统模型

基于OTFS波形的短波通信建模为图3所示。

图3 基于OTFS波形的短波通信系统模型Fig.3 HF communication system model based on OTFS waveform

在发送端，将调制后的符号复用在N×M的DD域帧中，得到DD域符号，记为x[k,l]，k=0,1,…,N-1;l=0,1,…,M-1;N和M分别是沿多普勒和时延维度的资源数量。经过ISFFT到TF域网格中，得到TF域符号表示如下：

(6)

DD域符号矩阵表示为X∈M×N，变换后的TF域矩阵式如下：

(7)

接着对信号进行传统的时频处理，其中时域采样周期为T，频域间隔为Δf，则TF域信号X[n,m]占据带宽MΔf，持续时间为NT，经海森堡变换转为时域信号：

(8)

式中，gtx(t)为发送脉冲，当其为矩形脉冲时，此变换相当于OFDM变换。时域发送信号的矩阵表示为：

(9)

在每个时域符号前加入CP，即完成发射端OTFS调制过程。

发射信号通过短波信道，信号到达接收端后，首先移除CP。随后，利用维格纳变换(Wigner Transform)，通过两步运算将时域信号转换到TF域。首先计算互模糊函数：

(10)

式中，grx(t)是接收脉冲，下一步进行采样，得到TF域接收信号：

Y[n,m]=Y(t,f)|t=nT,f=mΔf。

(11)

当接收脉冲为矩形脉冲时，信号处理方式等效于OFDM解调，即FFT处理：

Y=FMR，

(12)

其中，R和Y为接收的时域和TF域信号矩阵。

经过均衡后，得到接收端TF域的符号，均衡流程将在后文中具体描述。再利用辛傅里叶变换(Symplectic Finite Fourier Transform，SFFT)得到DD域接收信号：

(13)

(14)

3.2 DD域MMSE均衡

OTFS针对高多普勒场景，此时时域的信道脉冲响应变化快，无法视作恒定，会引起较大的ICI，传统一阶频域均衡不再适用。从线性均衡处理出发，OTFS可直接在DD域进行MMSE均衡[10]，接收机流程如图4所示。

将发射机的时域符号写为向量形式：

(15)

r=vec(R)=Htts+n=HttAx+n，

(16)

其中，

(17)

利用MMSE方式均衡接收到的时域信号，得到DD域的估计结果：

(18)

其中，

Gtd=[(HttA)H(HttA)+N0IMN]-1(HttA)H。

(19)

3.3 Block-MMSE均衡

式(17)为准对角矩阵，故可以分为N块进行检测，从而降低计算复杂度。此外，直接均衡到DD域难以实现分块，因此，可以首先均衡到TF域，再通过SFFT变换到DD域。通过Block-MMSE均衡[9]可实现上述操作。

根据式(2)，移除CP后的时域接收信号的第i列Ri可以表示为：

(20)

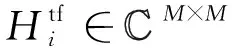
(21)

利用MMSE均衡得到TF域检测信号矩阵：

(22)

其中，

(23)

4 仿真结果分析

为了验证OTFS、单/多载波等不同信号体制的传输性能，通过Matlab仿真对不同波形经过短波信道的误码率进行了验证。根据ITU-R F.1487[12]给出的标准短波信道高斯散射模型，将信道建模为独立的两径等功率衰落，考虑多普勒效应的影响，选定3种不同频率扩展条件的信道模型：iturHFMM(信道0，最大多普勒偏移为0.5 Hz)、iturHFMD(信道1，最大多普勒偏移为1 Hz)和iturHFHM(信道2，最大多普勒偏移为10 Hz)。此外，考虑到传输时延影响，分别采用了5.12 s和1.28 s的交织方案。其他仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

在短波信道条件下，传统SC-FDE和OFDM波形的仿真结果如图5所示，对于多普勒扩展相对较低的信道0和1，OFDM的误码率性能较好。但对于高多普勒扩展的信道2，由于引入了较强的ICI，即使考虑低码率的编码和长交织仍不能有效恢复信号，因此后续仿真考虑基于Block-MMSE均衡的OFDM波形作为性能基线。

(a) 传统SC-FDE

对于多普勒扩展相对较高的信道1和2，在Block-MMSE均衡，图6给出了未编码的OFDM和OTFS波形的BER性能对比。从仿真结果可以看出，在不考虑编码的前提下，OTFS波形能够克服多普勒效应的影响，极大地改善信号检测性能。

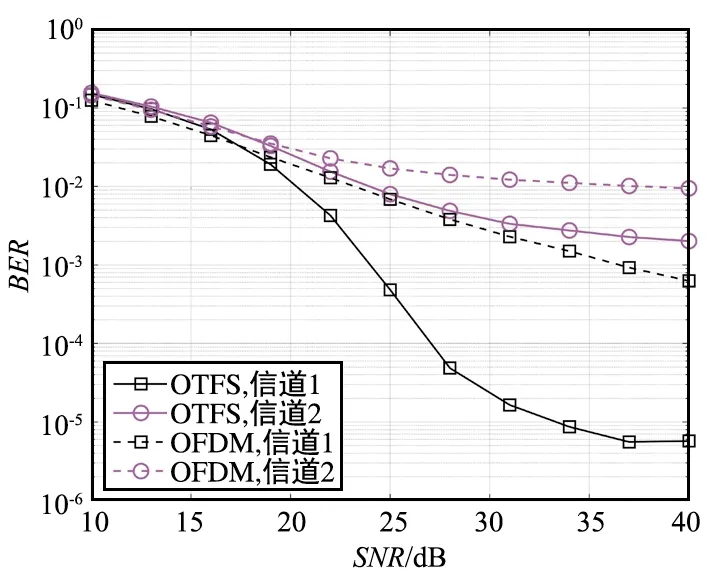
图6 未编码OFDM和OTFS波形的BER性能曲线Fig.6 BER performance curve of uncoded OFDM and OTFS waveforms

最后，针对有较高多普勒扩展的信道1和2，在考虑编码和交织的前提下，基于Block-MMSE均衡，两种波形的性能对比如图7所示。可以看出，基于信道1，低码率编码和长交织可以赋予OFDM波形足够增益，其性能接近甚至优于OTFS波形。但对于高多普勒扩展的信道2条件，OTFS波形能够取得显著的性能优势。此外，随着码率的增长和交织长度的降低，OTFS波形对短波信道传输的性能改善作用也愈发突出,这证明了OTFS波形适用于高多普勒效应的短波通信场景。

(a)1/2码率

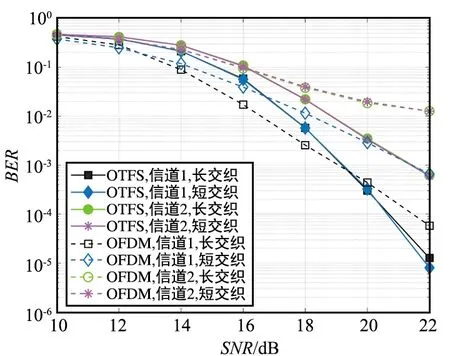
(b)3/4码率图7 编码交织后OFDM和OTFS波形的BER性能曲线Fig.7 BER performance curve of OFDM and OTFS after adding coding and interleaving module

此外，对比图5(b)、图6以及图7(a)中的OFDM相关性能曲线，采用Block-MMSE均衡时，信道1中相对传统一阶均衡性能得到提升，信道2中能够实现信号恢复而传统均衡下完全出错，故OFDM系统可在复杂度和性能之间权衡并选择合适的均衡方式。

5 结论

在短波信道下，多普勒扩展会引入载波间干扰，影响传统单/多载波体制的信号检测性能。针对这个问题，本文提出将OTFS波形应用于短波信道，通过计算机仿真，验证了OTFS波形在高多普勒扩展下的性能优势，揭示了新波形在短波信道中的应用潜力。后续工作将集中于在时延-多普勒域充分挖掘分集增益，以进一步提升短波通信性能。