一种确定水驱气藏动态储量及水体能量的新方法
2022-05-22成良丙吕昌盛杨永兴兰正凯
薛 婷 吉 雨 成良丙 吕昌盛 杨永兴 兰正凯
(1. 中国石油长庆油田公司勘探开发研究院,陕西 西安 710018;2. 低渗透油气田勘探开发国家工程重点实验室,陕西 西安 710018;3. 中国石油吉林油田公司勘探开发研究院,吉林 松原 138000;4. 中国石油长庆油田公司油气工艺研究院,陕西 西安 710018;5. 中国地质大学(武汉)资源学院,湖北 武汉 430000;6. 南京特雷西能源科技有限公司,江苏 南京 210000)
0 引 言
水驱气藏作为国内外油气田开发过程中较为常见的一类气藏,对此已经形成了一套较为成熟的开发理论与现场实践经验,主要通过控制生产压差延缓水体提早锥进,延长气藏无水开采期。但水驱气藏见水是阻止不了的趋势,产水不仅增加了地层渗流特征的复杂性,也给动态分析过程中动态储量计算及水体能量评估带来了挑战[1‐8]。近年来,国内外学者对水驱气藏动态储量计算以及水体能量评估进行了较为深入的研究,研究方法主要基于3 种不同的原理:一是基于物质平衡原理的方法,以R. J. Schilthuis[9]、 A. F. Van Everdingen 等[10]和M.J.Fetkovich 等[11]学者提出的物质平衡法为代表,仅需要生产动态资料以及地层压力测试值,计算过程较为简单,该类方法在常规气藏中运用较为广泛,但在水驱气藏中运用存在局限性;二是基于不稳定试井的方法,最为典型的即为弹性二相法[12],即利用不稳定压力进行外推得到动态储量及水体能量;三是基于经验及开发规律的方法,包括累计产量法[13]以及J.J.Arps[14]曲线拟合等方法。近年来,大量学者将以上方法进一步优化完善应用于现场实际。常宝华等[15]基于缝洞型油气藏裘比公式,利用无因次原理,拟合生产动态曲线,得到水体能量强弱参数;田冷等[16]利用3 种方法对比得到特定区块含水气藏的动态储量及水侵量;杜凌云等[17]基于物质平衡原理求解动态储量及水侵量的方法建立集成模型,通过最优化原理得到同时满足以上3种方法的目标参数。但是以上研究方法大多需要地层压力等较难准确获取的参数并且经过复杂的水侵量计算,不能广泛地应用于生产实际[18−19]。本文基于岩心相渗曲线,建立最优化模型,结合生产动态资料计算出动态储量与水体能量2 个参数,避免了大量的地层压力测试环节,通过实例计算验证了新模型的准确性,分析了水体能量对动态储量的影响,为水驱气藏开发理论研究与现场实践提供了新的方法。
1 水驱气藏物质平衡理论模型
气藏开发过程中,气相、水相以及岩石骨架始终能够满足物质平衡原理,当开发到某一阶段时,气藏剩余的天然气体积、目前存在的水相体积以及压力降低过程中岩石骨架和地层水膨胀的体积构成了气藏原始孔隙体积,可通过数学模型表达,即
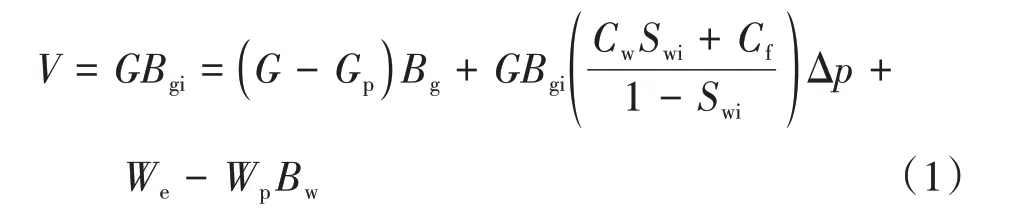
式中:V——气藏原始孔隙体积,m3;G——任一气藏动态储量或任一单井控制储量,m3;Bgi——原始压力条件气体体积系数;Gp——当前生产条件下气藏累计产气量,m3;Bg——任意压力条件下气体体积系数;Cw——地层水压缩系数,MPa−1;Swi——气藏束缚水饱和度,%;Cf——岩石骨架压缩系数,MPa−1;Δp——气井或气藏的生产压差,MPa;We——气藏目前水侵量,m3;Wp——某一压力条件下累计产水量,m3;Bw——地层水体积系数。
式(1)两边同除以GBgi得到
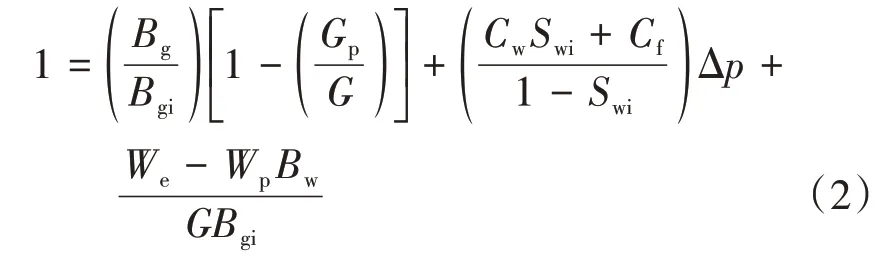
在气藏开发过程中,考虑到天然气的压缩性,结合气体状态方程,将气体体积系数的表达式代入
式(2)中转化得到用压力形式表示的物质平衡方程,即
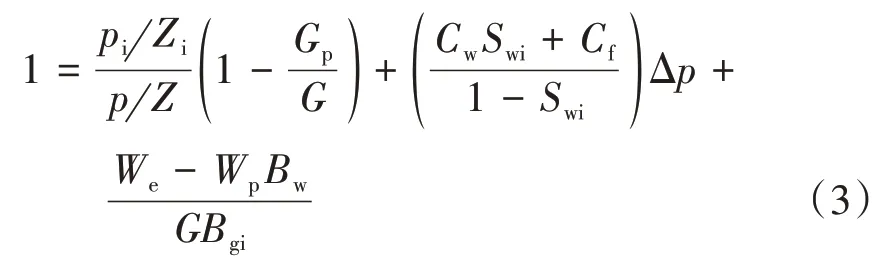
式中:pi——原始地层压力,MPa;Zi——气藏原始条件下气体偏差因子;p——任一压力条件下的地层压力,MPa;Z——任一压力条件下的气体偏差因子。
不考虑水驱气藏存在异常高压或异常低压的情况,一般情况下岩石与束缚水的膨胀作用相对于气体的膨胀作用可以忽略不计,因此,式(3)可简化为
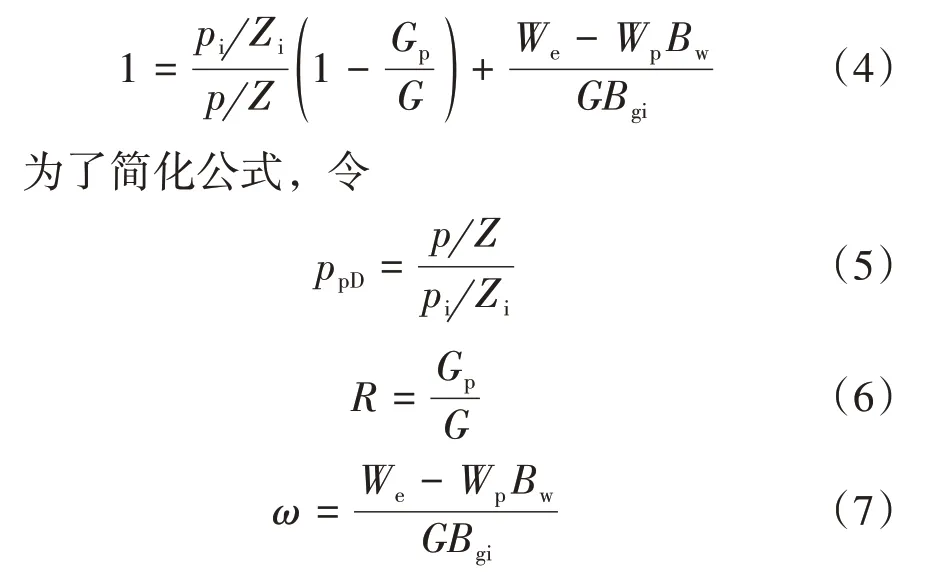
式中:ppD——无因次拟压力;ω——气藏存水体积系数;R——气藏采出程度,%。
因而式(4)可以简化为

其中n作为气藏水体能量强弱的表征,对于定容封闭气藏,气藏不存在水侵,n值趋近于无穷大(n→∞);对于刚性水驱气藏,气藏亏空的能量均由水的入侵来弥补,刚好达到采出与补充相等,n值为1;对于弹性水驱气藏,水体入侵仅能够补充一部分能量,气藏压力呈现缓慢下降趋势,在实际气藏开发过程中,水体能量参数n越大,水体能量越弱。
当气藏水侵后,在气井井口表现为气水同产,定义气水黏度比μR=μg/μw,气藏或气井的含水率可以表示为
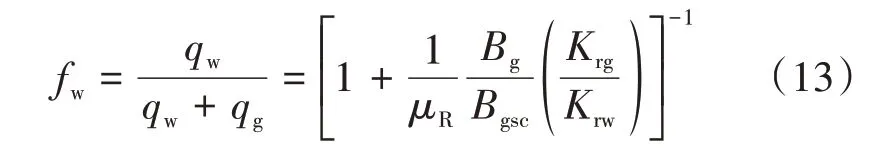
式中:fw——气水同产条件下气井含水率,%;qw——单井日产水量,m3;qg——单井日产气量,m3;μg——任一压力条件下天然气黏度,mPa·s;μw——任一压力条件下地层水黏度,一般为常数,mPa·s;Bgsc——标况下气体体积系数;Krg——气相相对渗透率;Krw——水相相对渗透率。
式(13)中气水两相相对渗透率比值Krg/Krw与气井含水率fw的关系可表示为
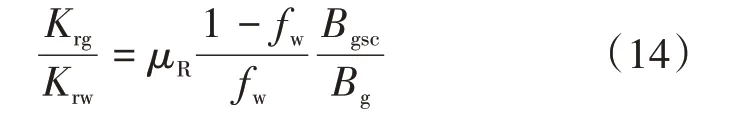
同时,气水两相渗流过程中,气相相对渗透率Krg随着气藏含水饱和度Sw的增大而减小,而水相相对渗透率Krw随着气藏含水饱和度Sw的增大而增大。
目前已有学者基于经验方法,总结了大量油气田开发的相关数据[20],获取了气、水两相相渗曲线与含水饱和度的关系,但是类似方法针对性不强,为了区别于不同气藏渗流特征,可以采用数据拟合的方式,得到气水两相相对渗透率比值Krg/Krw与含水饱和度Sw的理论关系式,即

同时,利用式(12)可以得到含水饱和度的表达式为
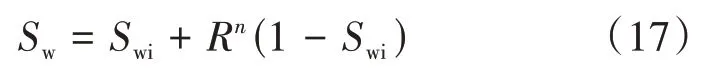
因为R=Gp/G,所以式(17)可以表示为Sw=Swi+(Gp/G)n(1−Swi),将该表达式代入式(16),f(Sw)可以表示为f(Gp,n,G),其表达式为
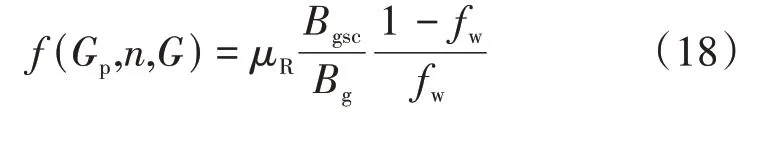
根据累计产气量与累计产水量分别对时间求导数,可以得到日产气量、日产水量,即qgsc=dGp/dt,qw=dWp/dt,因而,气井含水率fw与日产气量qgsc和日产水量qw关系式可表达为
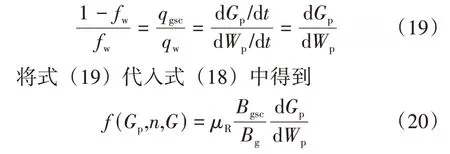
对式(20)利用分离变量法,采用定积分的方式可以得到
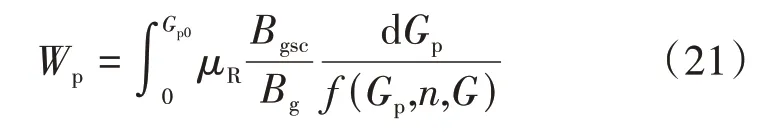
式中Gp0——某一时间段的累计产气量,m3。
2 水驱气藏动态储量及水体能量参数求解
结合气水相渗曲线以及式(21)即可得到水驱气藏动态储量及水侵强度指数综合数学模型,针对该模型要拟合的参数为动态储量G和水侵强度指数n,其求解步骤为:
(1)利用拟合方法拟合实验测试的气、水两相相对渗透率数据与含水饱和度的理论关系,得到其解析式,即Krg/Krw=f(Sw),并将其代入式(17)及式(18)中,可以得到目前单井的累计产气量Gp、动态储量G以及水体能量指数n的关系式f(Gp,n,G)。
(2)将单井的累计产气量Gp、累计产水量Wp作为已知参数,通过不断调整模型中的参数G、n的大小来与已知参数自动拟合,拟合一个最优的参数值,能够保证理论值与实际值的差距最小,即建立最优化求解方程式为
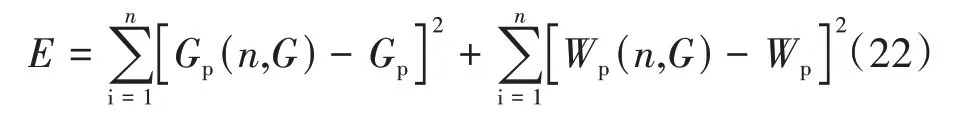
(3)在自动拟合过程中,需要给定参数G与n一个上下限值,给定上下限越合适,计算的时间越短。
3 应用实例
以气田中某水驱气藏生产井A 为例,该井目前油压34 MPa,气藏中部深度6 709 m,地层水黏度为0.8 mPa·s,目前地层压力条件下气体黏度为0.035 mPa·s,该井储层岩石测试相渗曲线如图1 所示,气藏束缚水饱和度为21%,其相关生产动态资料如表1 所示。
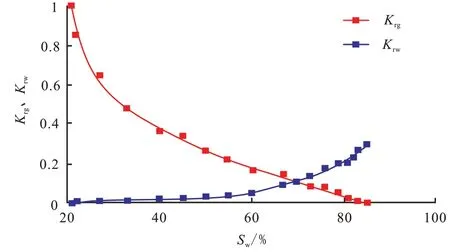
图1 A井储层相渗曲线Fig 1 Relative permeability curves of Well A

表1 单井生产动态资料Table 1 Production performance data of single well
利用已知生产井A 井的生产动态数据及相渗曲线拟合表达式,代入式(21)中,建立最优化求解模型,当单井理论累计产气量和理论累计产水量与实际生产值的误差最小时,对应的值即为单井动态储量及水体能量参数值,拟合得到单井控制储量G为11.2×108m3,水体能量参数n为2.5,其结果与物质平衡法等4 类经典方法对比,本文模型计算结果与4 类经典方法计算结果基本一致(表2),水体能量参数保持在2.5~3.0,验证了本文模型的准确性。

表2 本文方法与经典方法计算结果对比Table 2 Results comparison between new method and classical method
与前人研究的4 类方法相比,本文方法计算更为简单,仅需要矿场资料及岩心数据等参数,避免了复杂的地层压力测试过程,矿场普适性更好。
利用最优化模型求解得到的水体能量参数及动态储量,并将其代入式(21)中,对比理论拟合曲线与实际生产动态数据,如图2 所示,两者能够达到较好的拟合。
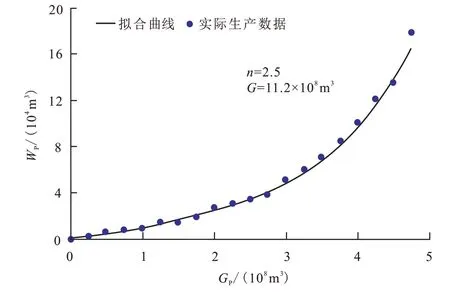
图2 A井单井控制储量及水体能量拟合Fig.2 Solution of reserves controlled by single well andwater energy of Well A
根据拟合的单井控制储量及水体能量参数,可以根据公式We=WpBw+GBgiRn进一步求得目前水侵量We为53.79×104m3。
为了进一步验证水体能量对水驱气藏动态储量的影响,当动态储量一定时,考虑不同水体能量大小的影响,如图3 所示。当水体能量参数较大即水体能量较弱时,在达到一定累计产气量的条件下,较小的产水量就可达到较大的动态储量;而当水体能量参数较小(水体能量较强)、累计产气量一定时,需要较大的产水量才能达到相同的动态储量,表明水体能量越强,气井见水后由于水封气的作用,气藏动态储量或单井控制储量均减小,影响最终采收率,体现了控水对含水气藏开发的重要性。
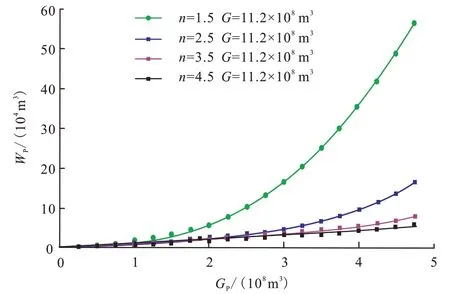
图3 不同水体能量对水驱气藏动态储量的影响Fig.3 Influence of different water energy on gas reservoir dynamic reserves
4 结 论
(1)利用水驱气藏物质平衡原理,定义了水体能量参数,并结合两相渗流条件下含水饱和度对气水两相渗流的影响,推导了累计产气量以及累计产水量的数学模型,并根据其未知数特性,建立了确定动态储量及水体能量的最优化模型。
(2)应用实例表明,新方法能够直接求解出动态储量及水体能量参数,与4 种经典的方法对比,结果基本一致,但是本文方法不需要压力测试数据及复杂的水侵量计算,更具有矿场适用性。敏感性分析表明,水体能量的增大能够使得水封气现象较为明显,进而降低气藏动态储量。
