考虑弹-筒柔性的潜载导弹弹射多体动力学分析方法

张子豪,王汉平

(北京理工大学 宇航学院,北京 100081)

0 引言

潜射弹道导弹具有隐蔽性好、生存力强、突防性佳、射程远、破坏性大等特点,是大国博弈的镇山之宝,一直深受青睐,其发射方式一般采用燃气-蒸汽式垂直弹射。在垂直弹射过程中,其弹道过程通常分为入水段、水弹道、出水段、空中段,其中前3 个阶段为潜射导弹所独有,也是关系其发射成败的关键。导弹和发射筒之间借助多圈适配器、密封环支撑,当导弹弹射入水时,导弹惯性较大,弹射过程中所受到的弹射力、重力、附连水惯性力以及水动阻力将导致较大的轴向载荷,对弹体刚性以及横向振动会产生不可忽视的影响。另外,由于载体运动以及导弹相对载体的运动,导弹还受横向流、波浪、适配支撑等条件影响,最终弹体和发射筒之间会产生相对旋转运动,因此水下弹射发射过程的动力学问题是一个复杂多场耦合且高度非线性的问题。

目前国内针对该问题的研究有两种思路:其一是对流体作用进行简化处理,列出导弹运动过程的显式方程,并结合计算流体动力学(CFD)软件的用户自定义函数(UDF)开发进行仿真分析;其二是对弹体与发射筒的接触作用进行简化处理,基于有限元技术开展流体与固体耦合的仿真研究。文献[5 -14]采用多相流模型,在考虑空化的条件下运用UDF 和动网格技术对弹体运动过程进行了数值仿真,并讨论了波浪、横向流等因素对弹体姿态的影响,但这些研究都只将发射筒简化为一种约束,没有考虑实际弹体和发射筒间复杂的相互作用;文献[15-17]利用牛顿定律列出了导弹的运动学和动力学方程组,并编程进行了仿真计算,但对水动力载荷及弹体与适配器间作用力的简化过于简单,与实际物理过程相差较大。文献[18 -19]对水动力和附连水惯性力进行了较为详细的表达,但是没有考虑发射筒和弹体之间的相互作用,只是简单认为发射筒对弹体施加了支撑力和摩擦力。程载斌等使用任意拉格朗日-欧拉(ALE)模型对导弹无攻角潜射过程进行了仿真,该模型无法适用于有攻角的情形,而实际的潜射状态攻角是一个无法回避的因素。刘传龙等使用切片法在考虑适配器作用的条件下进行了流体与固体耦合计算。裴譞等考虑了气密环的柔性与刚性弹体的耦合作用,研究了气密环的抗压刚度和结构尺寸对弹体出筒过程中横向振动的影响。尚书聪等面向不同艇速下适配器和气密环-减震垫两种横向支撑方式开展了对比仿真,研究了支撑方式对弹体姿态的影响,但模型中只考虑了适配器的抗压刚度,忽略了适配器抗弯刚度。

综上所述可知,已有研究均没有考虑发射筒的柔性影响。而弹体的柔性变形也将导致弹体的应力刚化,且发射筒柔性和弹体柔性将会产生交互耦合作用,这也是上述研究尚未涉及的问题。关于弹体与定向器间的相互作用,文献[24 -26]基于Euler-Bernouli 理论建立了柔性梁的偏微分方程,并自编程实现了移动物体作用下柔性梁振动的仿真研究,但是模型过于简单,与实际应用相去甚远。近年来,多体动力学仿真软件虽然具备了处理刚体与刚体、柔性体与刚体以及双柔性体之间接触建模的能力,但当复杂柔性体参与接触时,收敛性、稳定性较差,而且计算量巨大,直接制约了其应用范围。针对此问题,比较通用的方法是借助特定开发以简化接触建模,在保证精度和稳定性的同时大幅度降低计算量。Ambrogi 等基于ADAMS 平台开发了一种柔性点线高副,在卡车通过柔性桥梁的耦合模型中进行了验证,但是并未公开算法细节。王林鹏等基于三次样条曲线开发了一种柔性点线高副,并对移动导弹激励下的弹体发射架耦合振动模型进行了仿真分析,但该算法在由型值点坐标换算控制点坐标的过程中需要求解大型代数方程组,计算量较大。窦建中等开发了一种基于Hermite 插值函数的柔性点线高副,该算法省去了样条曲线繁琐的计算,但是应用对象是刚性弹体定向钮与柔性梁间的点线约束,而非双柔性结构。

本文面向潜射导弹弹体和发射筒的双柔性结构,提出一种高效、实用的动力学建模分析方法,采用修正的Craige-Bampton 法构建两结构的柔性,并基于Hermite 插值函数构建柔性点线高副,以实现柔性弹体与柔性发射筒间基于适配器的接触约束关系。基于Hermite 形状函数实现了适配器对发射筒的载荷等效作用、水动力以及附连水惯性力对弹体的等效简化处理,构建了同时考虑弹体和发射筒柔性的潜载导弹垂直弹射发射动力学模型,并以某算例进行了仿真校验,验证了该方法的有效性和优越性。

1 弹射发射动力学建模

某型导弹弹体通过4 圈适配器与发射筒相接触来实现适配导向约束,在发射起始时刻,导弹、发射筒和潜艇均以相同速度匀速航行。假设潜艇航行速度与洋流速度在同一平面,于是潜射导弹的弹射发射运动也可看作是一个平面运动。基于发射筒固连坐标系进行弹射发射动力学建模:原点位于发射筒筒底中心,导弹初始轴向为发射筒固连坐标系的轴方向,法向作为发射筒固连坐标系的轴方向,同时轴方向也是坐标系的运动方向。全局坐标系的方向与发射筒固连坐标系方向一致。弹体和发射筒的参数都按实际参数设置,导弹的速度按照实际测得的数据进行加载驱动。弹体和发射筒均按柔性体处理,弹体和发射筒之间的接触适配导向关系则通过柔性点线高副实现,其中柔性线以发射筒节点为型值点构造,弹体与适配器接触部位设置哑物体,哑物体中心就是点线高副中的点(本文仅阐述建模仿真的思路,在此忽略洋流的影响)。图1 所示为坐标系示意图,图2 所示为导弹结构及适配器分布图。图2 中,为弹体长度,为支撑面到弹尾距离,、、、分别为后适配器、第3 圈适配器、中适配器、上适配器到支撑面的距离。

图1 坐标系示意图Fig.1 Schematic diagram of coordinate systems

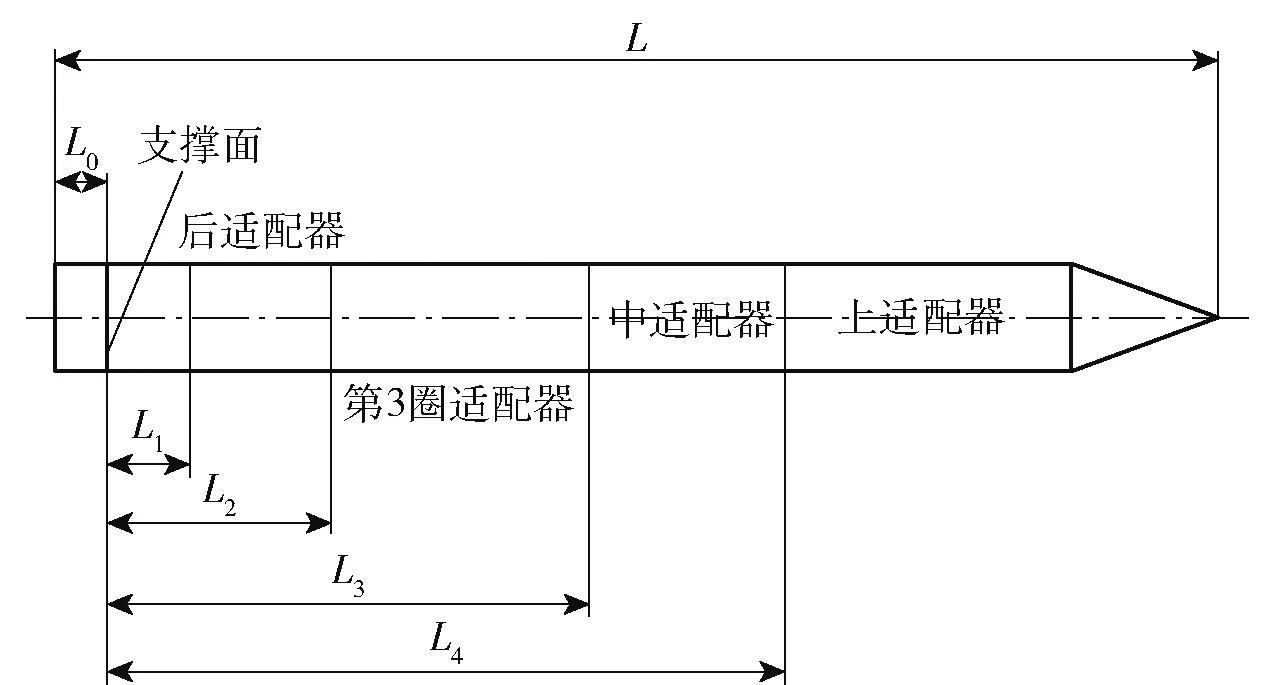
图2 导弹结构及适配器分布图Fig.2 Missile structure and adapter arrangement

1.1 发射筒和弹体的柔性化

弹体按离散质量点和等效梁相连接的方式进行简化,划分为41 段,梁参数由弹体截面半径、当量厚度、截面当量弹性模量以及截面当量剪切模量予以等效;发射筒按梁单元模型予以简化,其参数按发射筒的材料属性及截面参数予以赋值。将两部件用修正的Craige-Bampton 法进行柔性化处理,保留前20 阶固定界面的正交模态,并记录发射筒节点的初始坐标和对应的初始斜率,作为柔性线的初始型值点。其中,弹体的保留节点在4 圈适配器的挂接位置,发射筒的保留节点为发射筒在潜艇舱段中的悬挂处。

1.2 适配器作用的简化

整圈适配器的力学性能表现为抗压和抗弯刚度。适配器的变形情况可用其与弹体、发射筒相接触的两点与间相对位置关系来表示:dr为适配器的压缩量,在坐标系中适配器的初始厚度方向与全局坐标系轴方向重合,因此就是整圈适配器的弯曲角度,按线性处理,则有

式中:F为沿方向的抗压力;M为垂直平面与反向的抗弯力矩;为抗压刚度,k为抗弯刚度,可通过实验数据拟合得到。图3 所示为适配器作用示意图。图3 中,x、y分别为适配器与弹体接触截面的轴向和法向,x、y分别为适配器与发射筒接触截面的轴向和法向。表1 所示为各适配器刚度。

表1 各圈适配器抗压刚度和抗弯刚度Tab.1 Compressional and flexural stiffness es of adapters

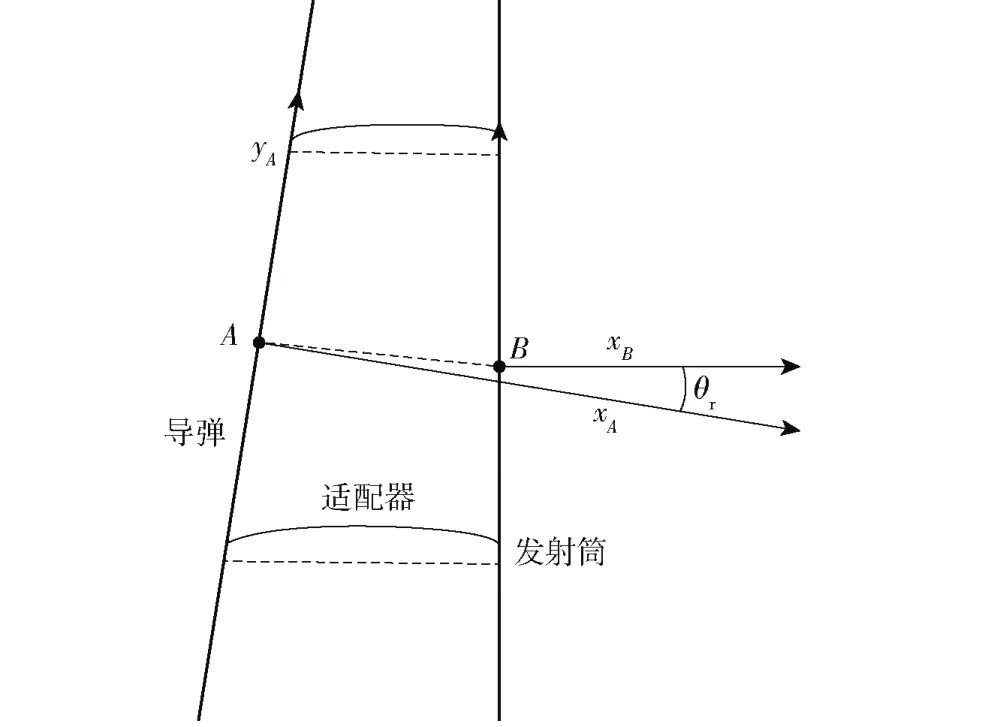
图3 适配器作用示意图Fig.3 Adapter force between missile and canister

1.3 发射筒和弹体基于4 圈适配器的接触约束

发射筒和弹体之间的真实状态是借助4 圈适配器的接触适配实现支撑和导向约束,在建模时按GForce 力元予以等效处理。简单起见,仅以某一适配器为例对模型进行阐述(见图4):由于动力学仿真ADAMS 软件中基于模态中性文件的柔性体不支持浮动Marker,按柔性体处理的弹体和发射筒均不能直接用作力的反作用物体,必须先在弹体与适配器的接口位置(即弹体的保留节点)处构建一个体积、惯性均非常小的哑物体1,并将其固定在弹体上,从而借助哑物体就可将适配器的载荷传递到弹体上,并且也可借助该哑物体来检测弹体适配器位置(即点)处的绝对位移和相对偏角。发射筒的节点坐标和对应位置处偏角可以实时提取,用以刷新柔性线,柔性线的动态变化就表征了发射筒的动态特性。建立哑物体2,哑物体2 与柔性线之间是点线高副约束(PTCV Joint),哑物体2 对应于适配器与发射筒的接触适配点,即点(初始状态与哑物体1 重合)。在哑物体1 与哑物体2 之间是在面约束(Inplane Joint),将哑物体2 约束在过哑物体1 中心且垂直于弹体轴线的平面上。提取哑物体1 与哑物体2 间的相对位移dr和相对转角,即可利用自定义的Gforce 力元将适配器的作用力等效加载到发射筒和哑物体1 上。

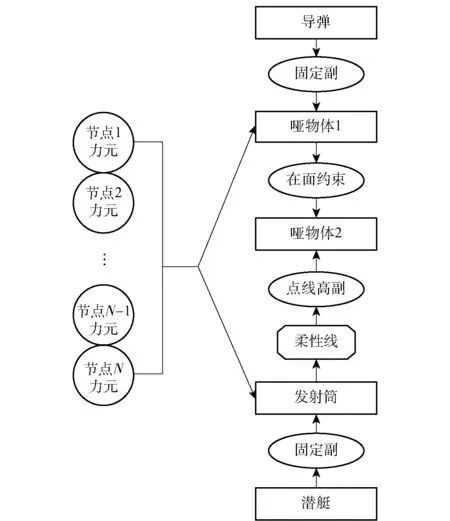
图4 弹体、适配器及发射筒间的力学模型拓扑结构Fig.4 Topological structure of mechanical model of missile,adapter and canister

1.3.1 柔性线的实现

柔性线的实现参考文献[28 -29],通过CBKSUB 子程序实时提取发射筒节点的坐标及对应点的偏角数据,利用公共变量将坐标及偏角数据传递给CURSUB 子程序,在CURSUB 中用Hermite 插值函数定义柔性线。图5 所示为弹体、发射筒间适配环节的数据流。

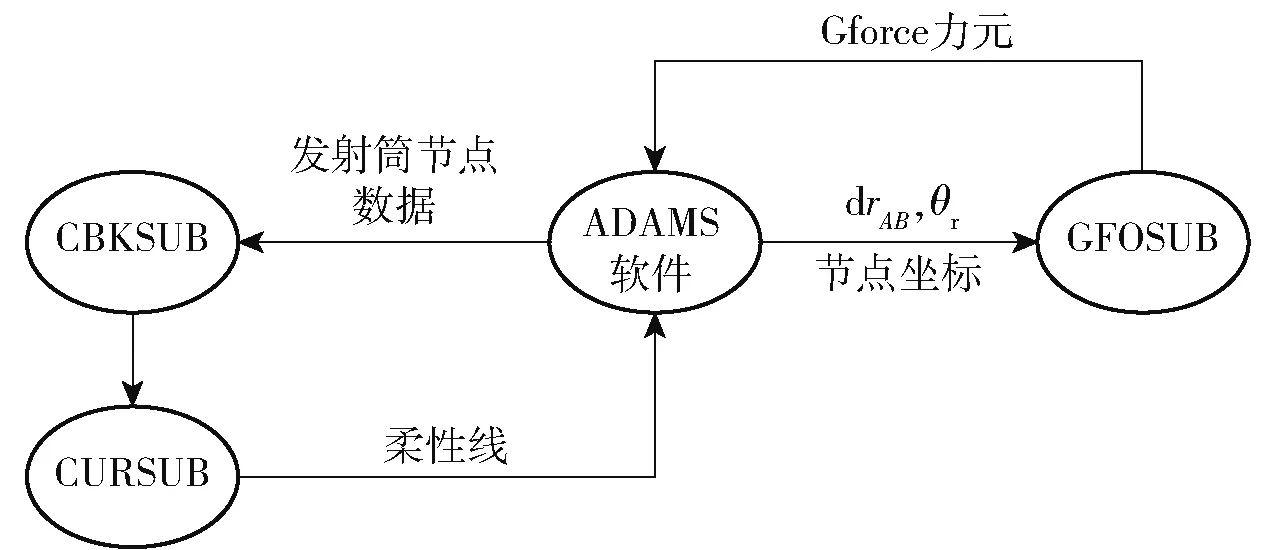
图5 弹体、发射筒间适配环节的数据流Fig.5 Data flow diagram of contact between missile and canister

1.3.2 载荷的加载

有关载荷加载,以前述适配器为例,需要在柔性发射筒的每个节点处都建立一个按GFOSUB 定义的GForce 力元。在GFOSUB 子程序中,首先提取dr与,计算适配器的抗压力和抗弯力矩。之后提取该节点坐标,根据坐标来判定该节点是否受力,如果受力,则从能量角度利用Hermite 形状函数将适配器作用力等效分配在发射筒跨越哑物体2 的邻近两节点上(见图6)。图6 中,F为施加在节点上沿全局轴方向的作用力,F为沿全局轴方向的作用力,为垂直平面的力矩,F为力F在全局坐标系下轴方向投影,F为力F在全局坐标系下轴方向投影。形函数表达式为

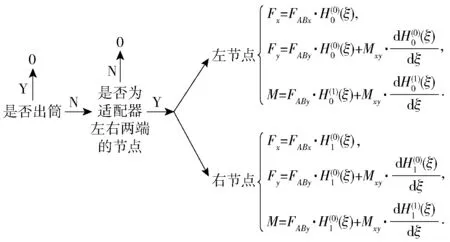
图6 载荷加载逻辑图Fig.6 Logic diagram of adapter loading

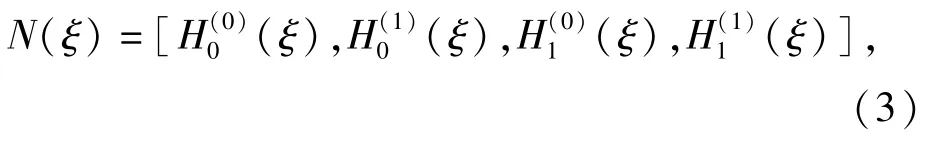
式中:为无量纲参数,

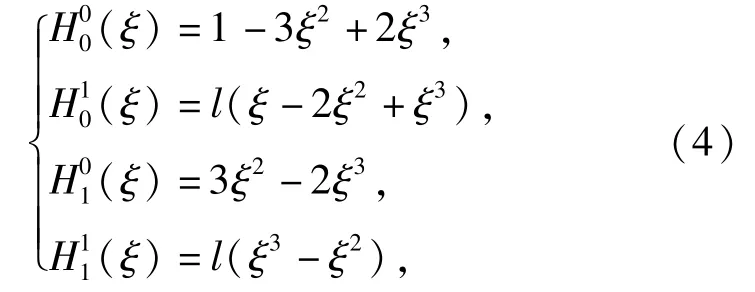
为有限段的长度。

1.4 弹体水动力、附连水惯性力的定义及加载

对弹体作用力的加载是在单元局部坐标系Oxy中开展的,表示第个节点,x轴为单元轴,y轴为单元法向。使用Gforce 力元进行加载,受力物体为弹体,施力物体为大地,将水动力及附连水惯性力的分布等效简化为单元两节点的集中力。

1.4.1 水动力的定义

1.4.1.1 整弹的水动力

水动力和水动力矩是与导弹姿态密切相关的。其中入水过程导弹所受横向阻力为

式中:为入(出)水深度占全长的比例;为导弹质心速度与轴向的夹角(攻角);为弹质心速度;ξ()为横向水动力入水系数;C(,)为横向水动力系数;为海水密度;为导弹的参考面积。

入水过程中,由横向阻力产生的水动力矩为

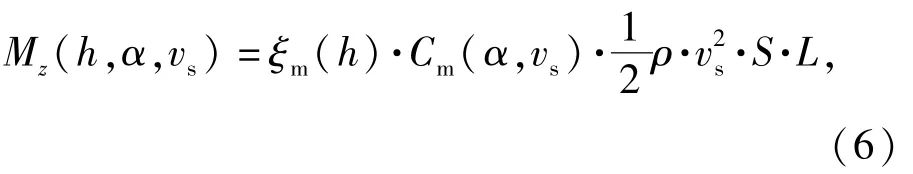
式中:()为俯仰水动力矩入水系数;(,)为俯仰水动力矩系数。

入水过程轴向水动阻力为

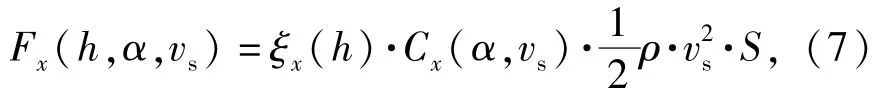
式中:ξ()为轴向水动力入水系数;C(,)为轴向水动阻力系数。

在出水过程导弹所受横向阻力为

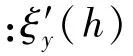
出水过程中,轴向水动阻力为

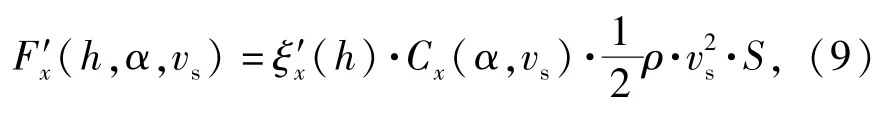
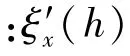
1.4.1.2 水动力的分布

在入水段,横向水动力在轴向方向上的分布为

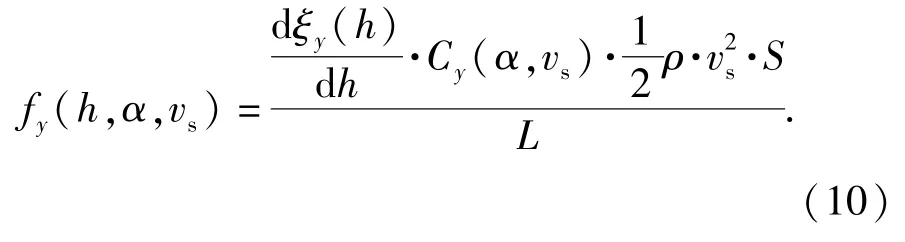
水动力矩的产生主要是由于水动力载荷的轴向分布引起,因此在考虑横向水动力载荷的轴向分布之后自然就包含了水动力矩载荷。

入水段轴向阻力在轴向的分布为

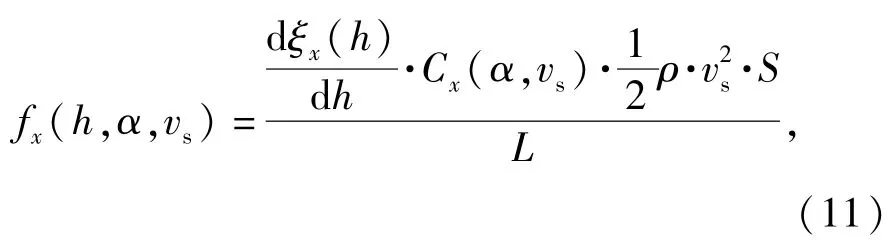
在出水段阶段,横向水动力在轴向的分布为

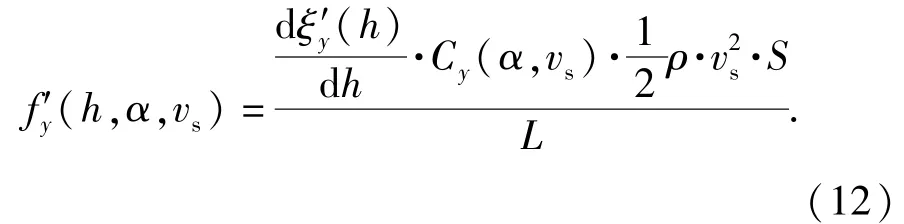
出水段轴向阻力在轴向方向上的分布为

考虑到艇体的横向速度,弹体的攻角和速度模的平方表达为

式中:v、v、θ分别为发射筒坐标系下单元的横向速度、轴向速度、角位移。

1.4.2 附连水质量惯性力的定义

入水过程中轴向附连水惯性力为

入水过程中横向附连水惯性力为

式中:λ(,)、λ(,)分别为轴向和横向附连水质量的入水系数;a、a分别为当地节点在其局部坐标系中的轴向、横向加速度。

入水过程中轴向附连水质量惯性力在轴向的分布为

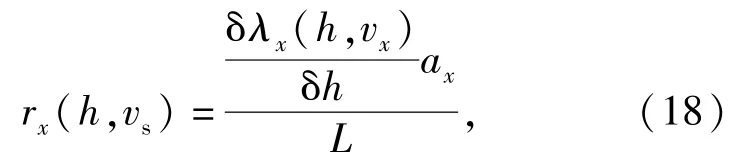
入水过程中横向附连水质量惯性力在轴向方向上的分布为

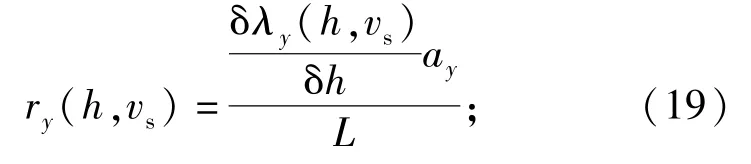
出水过程中轴向附连水质量惯性力为

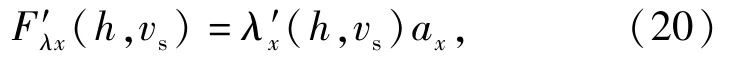
出水过程中横向附连水质量惯性力为

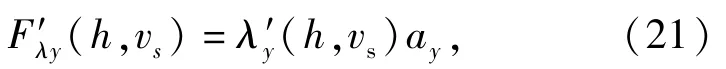
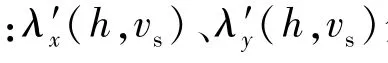
出水过程中轴向附连水质量惯性力在轴向的分布为

出水过程中横向附连水质量惯性力在轴向的分布为

1.4.3 分布力加载

弹体有限段的划分利用1.1 节柔性化处理时进行的分段。有限元变形的描述仍采用Hermite 插值函数,但是坐标系使用有限段局部坐标系,形函数同(3)式。

假设单元12 段和23 段上节点1、节点2 和节点3处的分布力大小分别为、、,而节点处的分布力f的表达式在入水段为

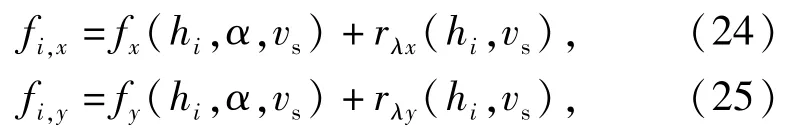
而在出水段则为

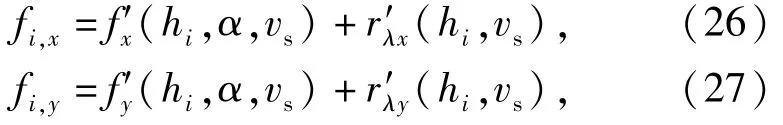
式中:h为对应于节点的入(出)水高度比。

将分布力按线性分布予以近似,则在12 段上单元分布力表达式为

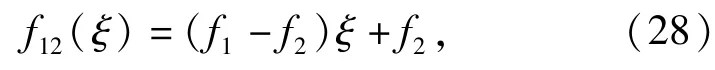
在23 段上,单元分布力表达式为

图7 为有限元示意图,其中,、分别为23 单元、12 单元实际入水部分占有限段长度的无量纲参数。

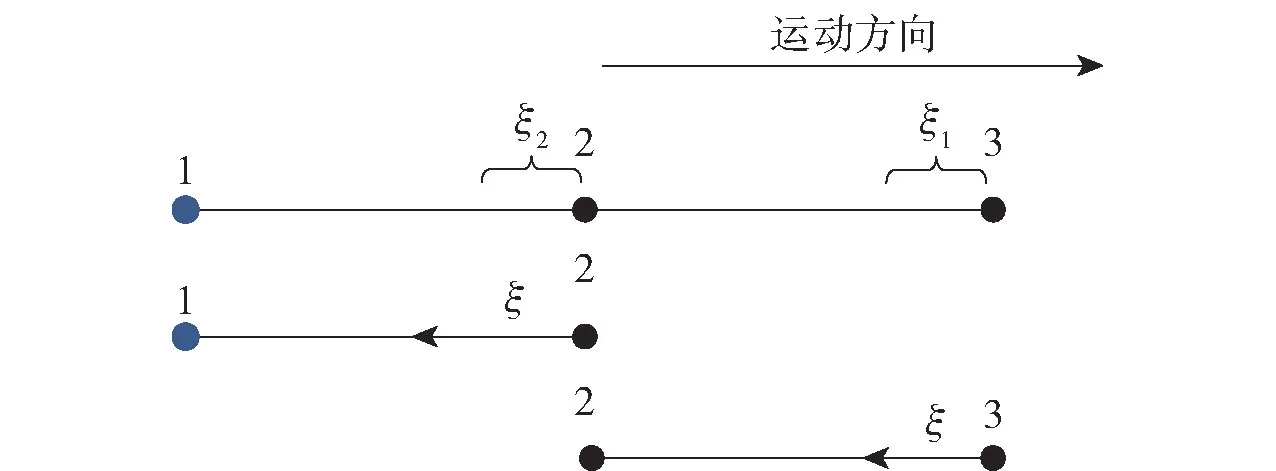
图7 有限段示意图Fig.7 Schematic diagram of finite element

把发射筒筒口坐标和作为研究对象的该有限段节点坐标、、进行比较,根据比较结果得出该有限段所处的位置。图8 展示了有限段位置的4 种情况,其中(1)、(2)、(3)、(4)分别表示两个单元都入水、右单元入水、左单元部分入水、右单元部分入水;两个单元都在筒内。

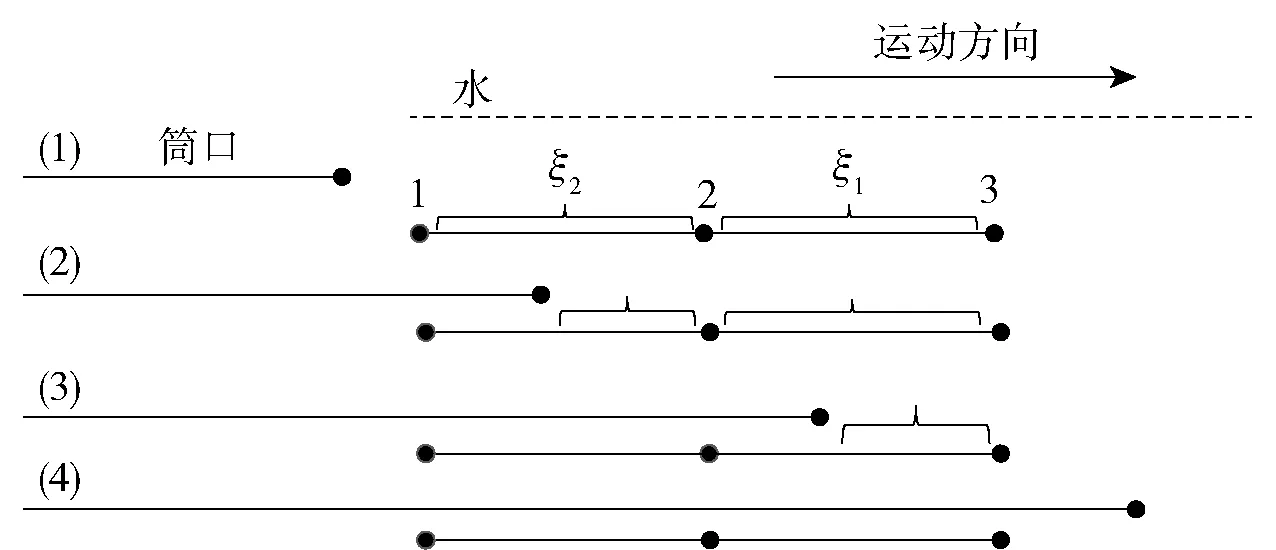
图8 不同位置有限段示意图Fig.8 Schematic diagram of finite elements in different positions

根据所处位置,、的计算方式如下:

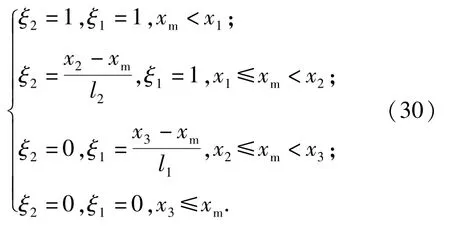
式中:、分别为12 段和23 段的长度。

根据1.3.2 节中利用Hermite 形状函数对有限段变形的描述,可计算出入水段节点2 处等效的集中力与集中力矩:

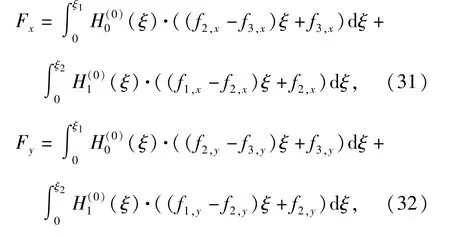
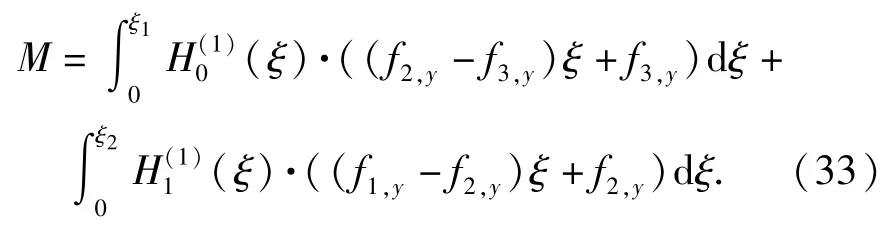
使用GFOSUB 子程序定义GForce 力元,即可完成载荷的加载。

2 仿真校验

对所有数据都进行无量纲化处理,处理方式如下。

无量纲时间为

式中:为弹体出筒时刻速度。

无量纲力为

式中:为弹体质量;为重力加速度。

无量纲力矩为

无量纲位移为

无量纲速度为

无量纲角度为

式中:为弹体俯仰角;为弹体出筒时刻质心的角速度。

无量纲角速度为

式中:为俯仰角速度。

初始时刻弹体与发射筒重合,计算时采用实测的速度-时间历程作为导弹的驱动,艇速为3.5 kn,仿真计算导弹入水、水弹道、出水的全过程,结果如图9～ 图12 所示,关键时间节点导弹姿态如表2所示。

由图9 可知,弹体在推力作用下加速离筒。由图11、图12 结合表2 可以看出,随着弹体入水体积的增加,弹体受到的水动力载荷会不断增加,导致姿态变化,随着出筒过程中适配器的脱离,弹体运动更加自由,姿态变化会进一步加剧;出水后,随着出水体积的增加,弹体的姿态变化会变缓。

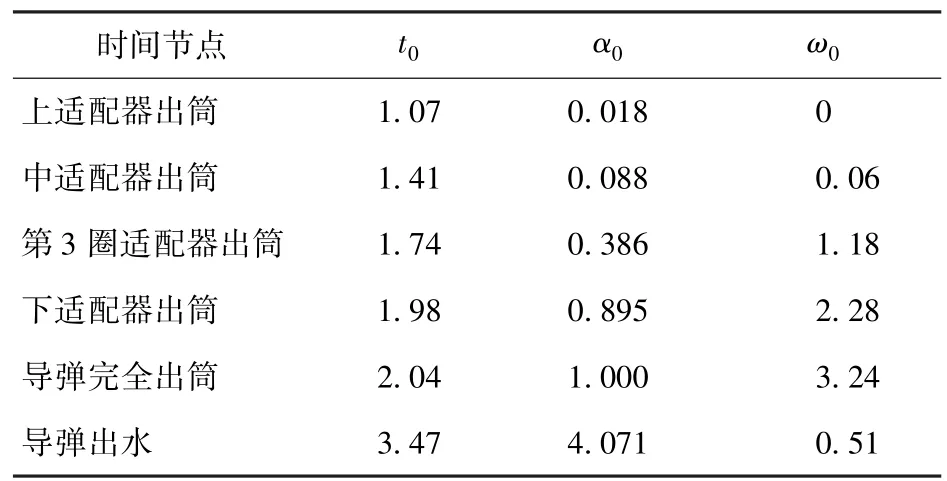
表2 关键时间节点的导弹姿态Tab.2 Missile attitude at critical time

图9 全过程仿真弹体质心速度-时间历程Fig.9 Velocity-time curve of the center of mass of missile (whole trajectory)

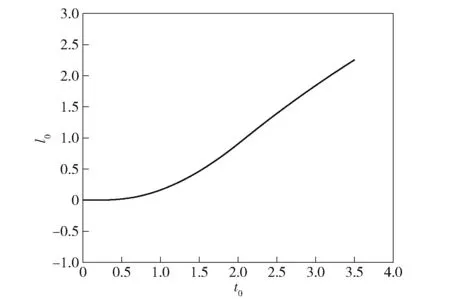
图10 全过程仿真弹体质心位移-时间历程Fig.10 Displacement-time curve of the center of mass of missile(whole trajectory)

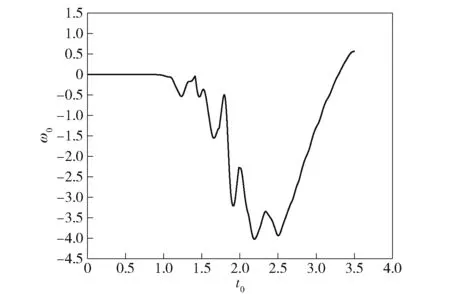
图11 全过程仿真弹体质心俯仰角速度-时间历程Fig.11 Pitch angular velocity-time curve of the center of mass of missile(whole trajectory)

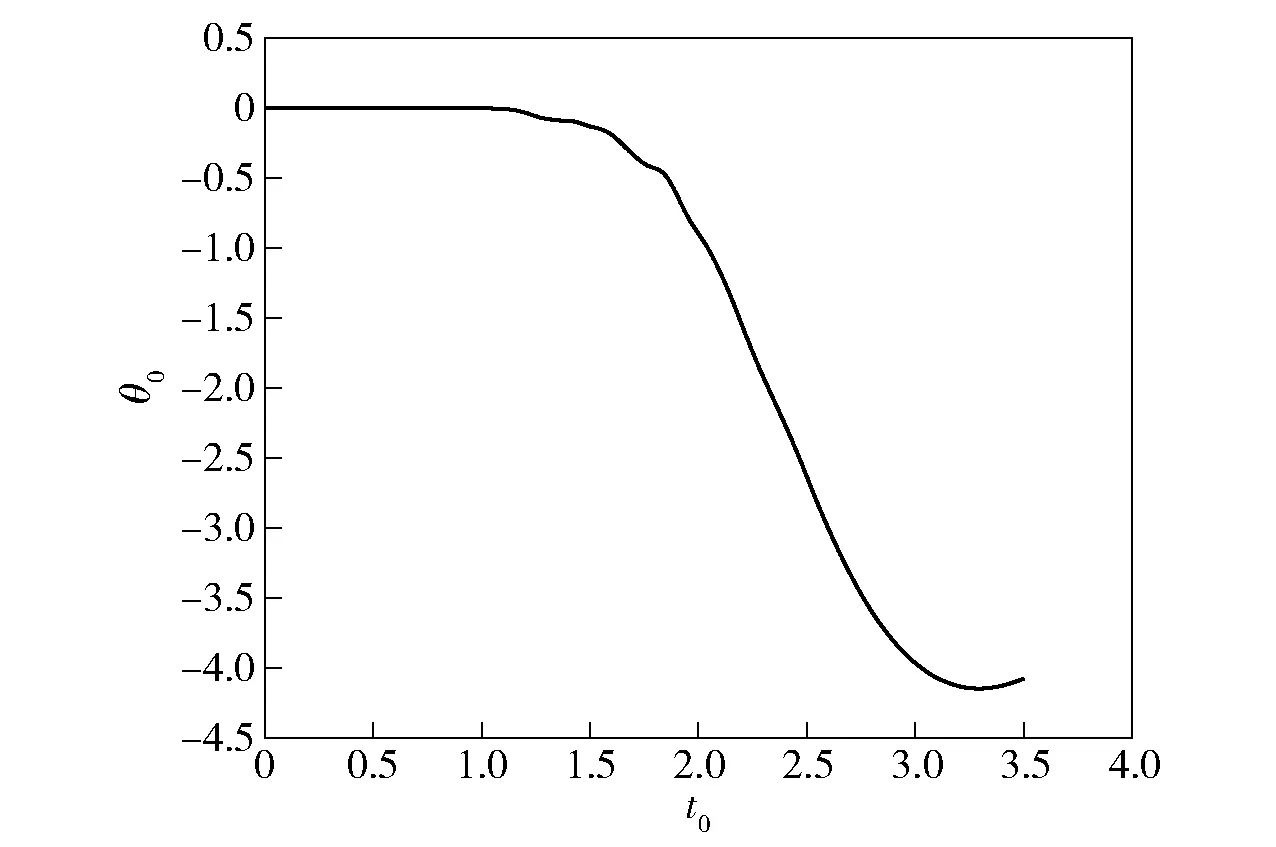
图12 全过程仿真弹体质心俯仰角-时间历程Fig.12 Pitch angle-time curve of the center of mass of missile(whole trajectory)

将仿真数据与实验结果进行对比可知,实验测得的数据只有的前2.26,包括入水段和水弹道的一部分,截取柔体仿真数据的前2.26,并附上刚体仿真数据。对比结果如图13、图14 及表3 所示。

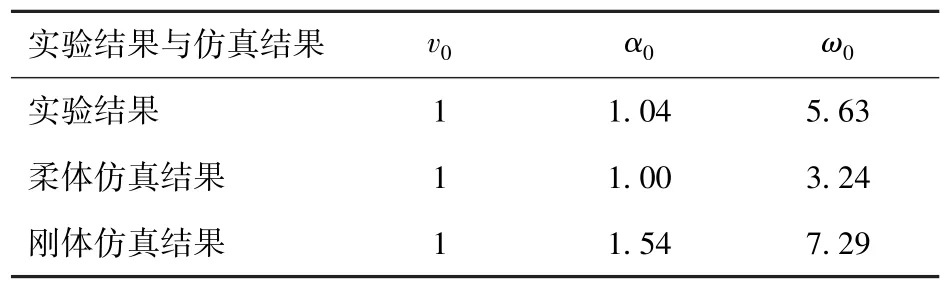
表3 出筒时刻弹体运动信息对比Tab.3 Comparision of attitudes of missiles out of cainster

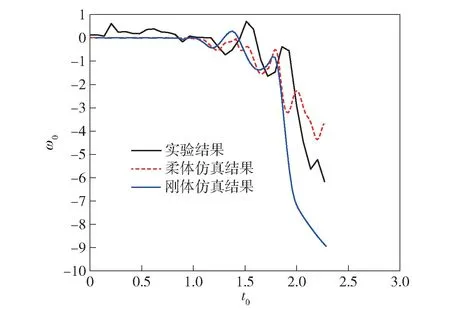
图13 俯仰角速度-时间历程对比Fig.13 Simulated and experimental pitch angular velocity-time curves

由图13、图14 可以看出:柔体仿真曲线与实验曲线吻合良好,从而证明了仿真模型的有效性。对比柔体仿真与刚体仿真,柔体仿真平均误差和最大误差是刚体仿真的0.2 倍。相比刚体模型,柔体模型的结果与实测数据更加接近。值得一提的是,柔体仿真占用计算资源并不多,本算例用笔记本电脑I5 六核处理器10 min 完成计算,与刚体模型的计算量接近。

图14 俯仰角-时间历程对比Fig.14 Simulated and experimental pitch angle-time curves

仿真给出了四圈适配器的受力(见图15),中适配器受力状况最为恶劣,受到的最大无量纲载荷为0.078,后适配器的受载方向与前3 个相反,符合实际弹体产生俯仰角后适配器的变形情况。图16 和图17 分别为全过程俯仰角、俯仰角速度随时间变化曲线。

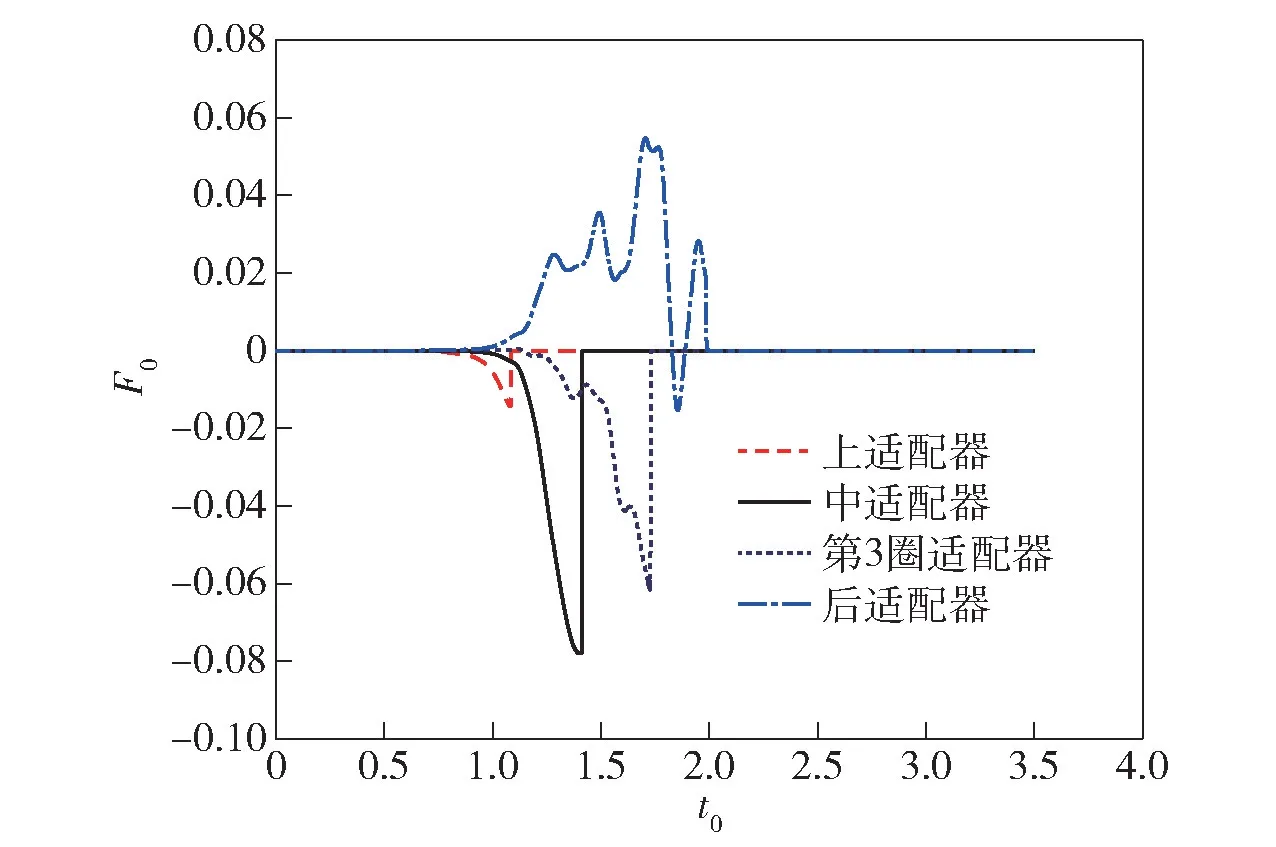
图15 全过程适配器载荷-时间历程Fig.15 Curves of load on adapters (whole trajectory)

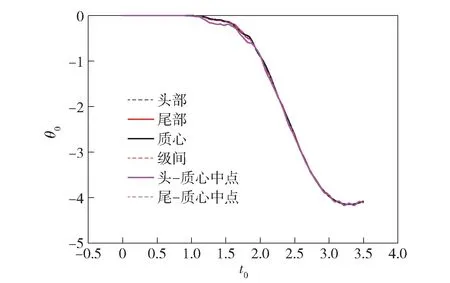
图16 全过程俯仰角-时间历程对比Fig.16 Comparison of pitch angles at the center of mass,head and tail of missile (whole trajectory)

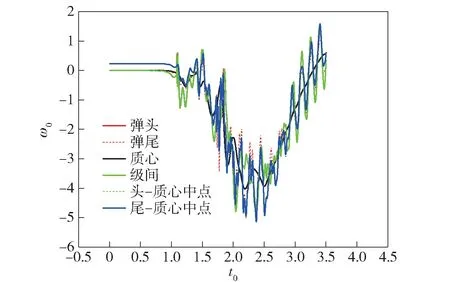
图17 全过程俯仰角速度-时间历程对比Fig.17 Comparison of pitch angular velocities at the center of mass,head and tail of missile (whole trajectory)

由图16、图17 可以看出,弹体不同位置处的运动情况是有明显差异的,证明柔体仿真是有必要的。结合图11、图13、图16、图17 可以看出,柔体仿真相比传统刚体仿真不仅可以捕捉弹体不同位置的运动状态,还可以提供丰富的振动特性。弹体柔性是由固定界面模态综合法计算出的前20 阶模态表达的。

为了验证本文方法的适用性,分别对航速为1.5 kn、2.5 kn、3.5 kn 进行仿真,研究潜艇航行速度对俯仰角和俯仰角速度的影响,仿真结果如图18、图19 所示。

由图18 可以看出,航行速度对弹体出筒姿态有较大的影响,随着航行速度的增加,弹体的俯仰角速度和俯仰角会显著增加,但是曲线的变化趋势基本相同。

图18 全过程俯仰角-时间历程对比Fig.18 Comparison of pitch angles in different simulation cases (whole trajectory)

由图11、图13、图19 可知:前2.5 弹体有明显的振动,这是由适配器的脱离引起载荷剧变所致;后半段弹体已完全出筒,部分出水,随着水动力载荷的减小,响应幅值减小,表现为俯仰角速度曲线的相对平滑。从图19 中可以看出,质心的振动不如其他位置振动明显,可见弹体振型叠加后在质心位置有相互削弱甚至抵消的效果。

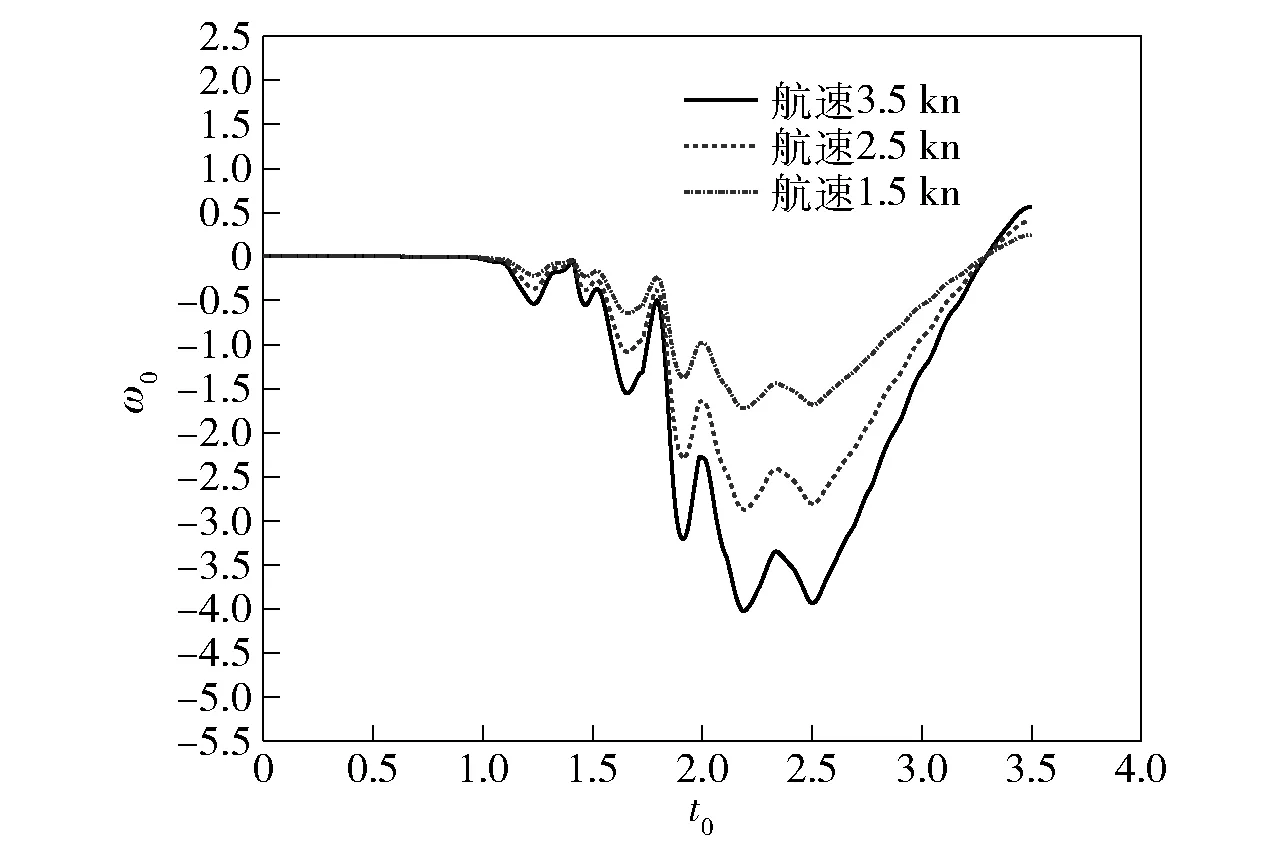
图19 全过程俯仰角速度-时间历程对比Fig.19 Comparison of pitch angular velocities in different simulation cases(whole trajectory)

3 种航速下适配器的受载极值都发生在适配器中(见表4)。从表4 中不难看出,随着航行速度的增加,适配器的载荷会显著增加,但各圈适配器受载时间历程的趋势相近,且后适配器的受载方向与前3 圈适配器相反。

表4 各工况适配器载荷极值Tab.4 Max load on adapters in different conditions

3 结论

本文针对潜载导弹弹射发射提出了一种可以同时考虑发射筒、弹体柔性的动力学快速分析方法。将柔性点线高副模型拓展应用于潜射导弹的垂直弹射发射动力学建模,模型中同时考虑弹体和发射筒的柔性,基于Hermite 形状函数对适配器的抗压力和抗弯力矩进行等效分配,并编程加载到发射筒中跨越适配点的邻近两节点。基于Hermite 形状函数及弹体所受水动力、附连水惯性力的线性分布,假设对水动力、附连水惯性力进行等效加载,实现了潜射导弹垂直弹射发射动力学分析。针对某潜射弹的动力学仿真结果表明仿真姿态与实验数据吻合较好,验证了建模方法的实用可信,且模型简洁、稳定、高效,为潜载弹的弹射发射建模提供了一种新思路,为拓展柔体之间接触的简化建模提供了新途径。得出如下主要结论:

1) 在水动力、附连水惯性力的单元线性分布假设基础上,采用Hermite 形状函数和有限元理论将分布的水动力和附连水惯性力向弹体节点等效简化的处理方法,具有足够的精度,满足使用要求。

2) 将弹体在适配器位置处相对于发射筒的运动位移及姿态变化所计算得到的适配器力和力矩,用Hermite 形状函数向发射筒跨越适配器点的最邻近两节点予以等效简化,算法可信,结果合理。

3) 弹体不同位置的运动角度差异明显,表明弹体在运动过程中存在高频振动,也进一步表明柔体仿真十分必要。

4) 本文仿真方法相比刚体仿真计算结果更接近实验数据,相对于传统有限元方法仅需很少的计算资源。

5) 潜艇行速度研究结果表明:潜艇航行速度会显著影响导弹姿态以及适配器的受载大小,但导弹的姿态历程趋势相同,仅影响具体的量值,速度越大,姿态偏差越大。