全波形矩张量反演方法及其在矿山微震监测中的应用
2022-05-22简筝马举刘晓勇国栋
简筝 马举 刘晓 勇国栋
摘要:微震事件被动监测技术和震源定位技术大大提高了人们对岩体破裂和断层活动的理解。针对某矿山微震事件频发、岩体垮落严重等问题,采用一种新的包含频域拟合和时域拟合的全波形矩张量反演路线,探寻适合该矿山三维监测网络下的微震事件矩张量反演方法,确保能够快速计算矿山微震事件的矩张量参数及断层面解,能够对矩张量进行快速分解并识别岩体的破裂类型。根据计算,该矿山在不同带通滤波器下反演所得的全波形矩张量分解出的双力偶断层面解是一致的,均以剪切为主。
关键词:微震监测;全波形;矩张量;反演;剪切
引 言
微震事件是指发生在较小空间尺度(几米至几千米范围内)上的非常弱小的地震事件,该类事件既可由构造应力引发,也可由人为因素导致的应力改变引发[1]。在地震学中,微震事件被定义为未能被人体感知到的地震事件,一般指矩震级(MW)在4级以下的地震事件[1]。
根据GIBOWICZ等[1]的描述:全球已观测到的矿山微震事件大致可分为2个大类:一类与矿山的开采活动直接相关,如与采场的破裂变形相联系的微震事件;另一类和大的地质间断面的运动相联系。这种分类方法的重要意义在于由开采活动直接诱发的微震事件在很大程度上与采矿导致的岩体破坏的能量改变相关,也就是说由开采导致的微震响应直接与开采尺度成正比。但是,对于由开采活动间接触发的微震事件而言,岩体已经处于不稳定状态,一个很小的扰动能量即可触发并导致大尺度能量释放和大范围的岩体破坏,造成较大震级的微震事件发生。
微震事件的被动监测技术和震源定位技术大大提高了人们对岩体破裂和断层活动的理解[2-6]。依据微震监测技术,目前已经可以准确分析矿山的地震灾害,包括获知微震事件的震级信息[7],频度-震级信息(b值分布特征),视应力及岩体破裂特征[8],震级-时间历史分布特征[9],震源位置及聚类分布特征,事件S波能量与P波能量比值分布特征等。
但这些研究还不足以提供震源处岩体的断裂机制,还不能有效分析断裂的发育过程,不能分析出哪些微震事件由开挖过程直接诱发,哪些事件是在开挖过程中由应力转移触发断层的活化导致,也不能得出应力场的分布规律及岩体破裂面的产状信息。本文以微震事件全波形信息为基础,以矩张量反演为技术手段,分析矿山微震事件的震源机制及导致微震事件的地质力学条件,确定微震事件的诱发机理及其发育过程,以期为矿山治理微震灾害提供技术支撑。
1 力学机理与震源机制
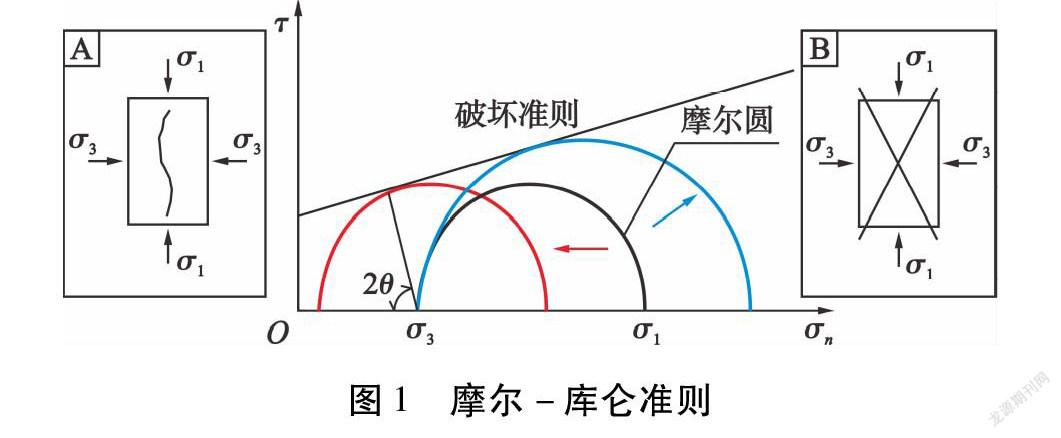
岩体的应力状态可由如图1所示的摩尔-库仑准则表示,图1中黑线半圆(摩尔圆)表示岩石的原始稳定应力状态,该半圆上的点表示不同旋转角度下的正应力(σn)与剪应力(τ)值,如沿水平軸的应力值描述最大主应力(σ1)和最小主应力(σ3)的值,此时的剪应力值为零。该摩尔圆的包络线斜率值与该材料的摩擦系数相关,截距值与内聚力和抗剪强度相关。
当摩尔圆与包络线相切时,岩体发生破坏,该处的应力释放是微震事件地震波的能量源。岩体破坏可能是最大主应力增长导致的,如长期构造应力导致的岩体变形(如图1所示的蓝线摩尔圆),也可能是最小主应力值降低导致的,如水力压裂或岩体开挖导致的岩体破裂(如图1所示的红线摩尔圆)[10]。
纯拉伸条件下的岩体破坏机制(正应力值为负值)如图1-A所示,纯剪切条件下的岩体破坏机制(正应力值为正值)如图1-B所示。由于岩体破坏方式的不同,应力释放过程产生的能量辐射也不同,拉伸破坏释放的能量较少,因此岩体拉伸破坏型微震事件的震级通常较小,事件所辐射出的地震波中高频成分占比相对较大[10]。
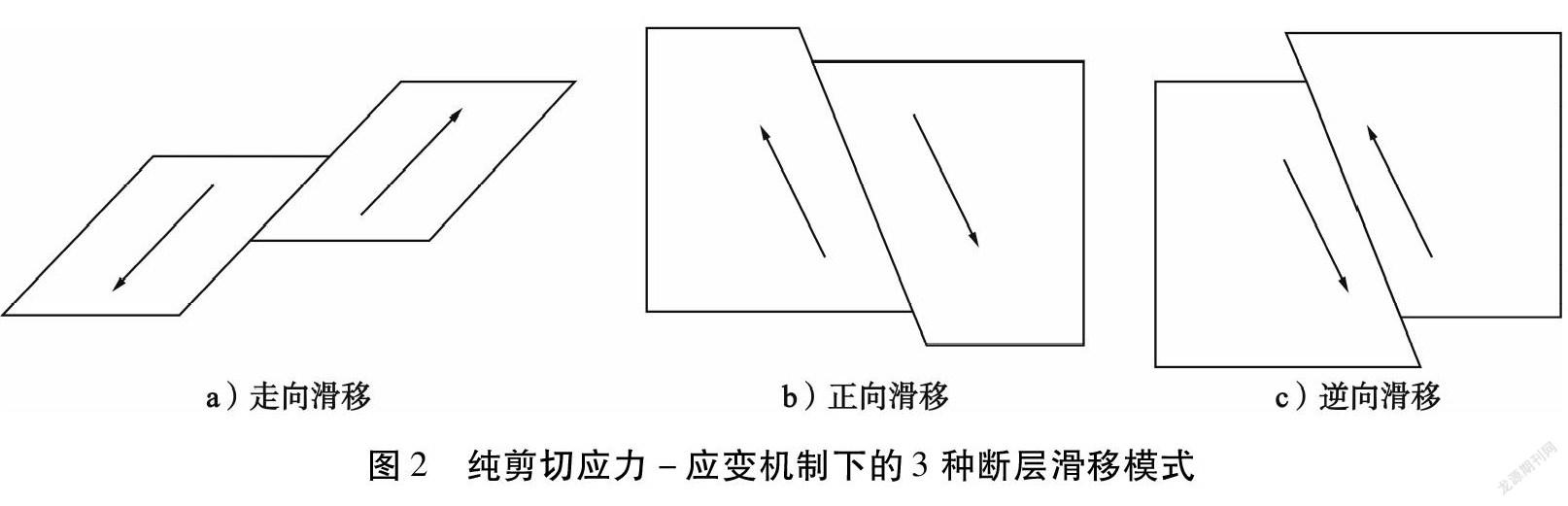
根据主应力之间的比值,纯剪切破坏可以分为3种应力-应变机制:走向滑移、正向滑移和逆向滑移,如图2所示。以σV表示垂直应力,最大水平应力表示为σH1,最小水平应力表示为σH2。当σV>σH1>σH2 时,岩体破坏机理为正向滑移;当σH1>σV>σH2时,岩体破坏机理为走向滑移;当σH1>σH2>σV时,岩体破坏机理为逆向滑移[10]。
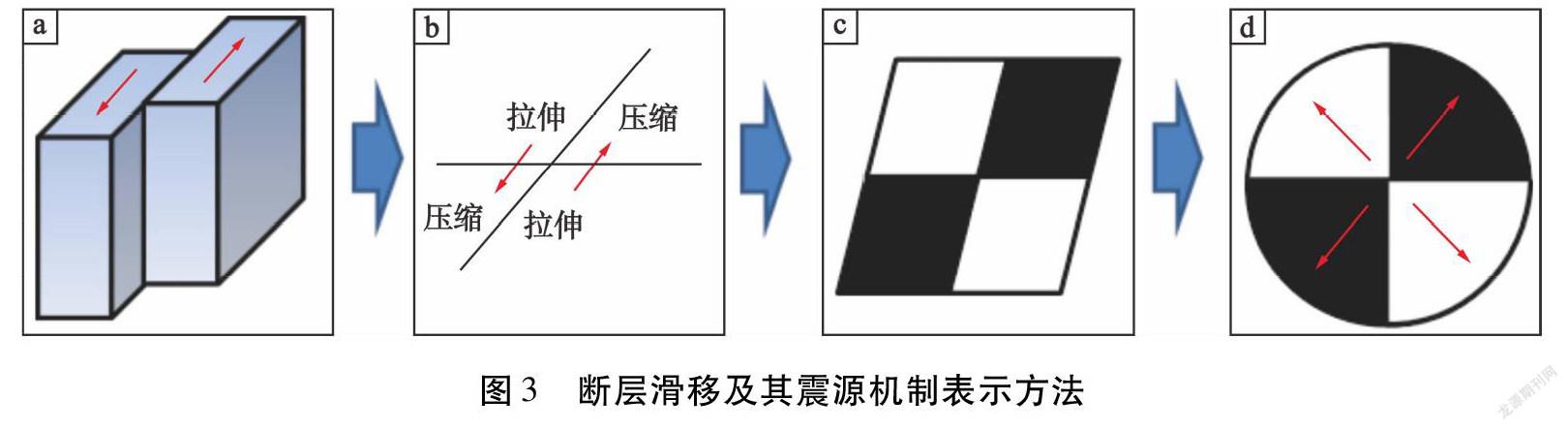
震源机制(Earthquake Source Mechanism)是指震源区在地震发生时的力学过程。走滑断层震源激发模式及其震源机制表示方法如图3所示。当断层发生错动时,上下盘岩体依据其所处断层面的相对位置,或发生压缩变形,或发生拉伸变形。当分别以黑色和白色表示压缩区和拉伸区时,该断层滑移的震源机制可由图3-d表示,因此当根据地震波波形信息得到如图3-d所示的震源机制时,可以反推该震源处的应力-应变变化机制及岩体破裂面的产状信息。
2 全波形矩张量反演方法
随着微震记录数据质量的提高和计算理论的改进,微震学的研究朝着定量解释观测数据的方向发展。微震记录包含震源、传播路径和地震记录仪器响应的信息,是这3种效应的综合结果。不管是研究震源的破裂过程,还是探索地震波在岩体介质中的传播,除了需要对仪器记录时产生的畸变进行修正外,还需要把震源效应与路径效应“分离”开。随着数值计算能力的提高和对地球内部结构了解的深入,当前已经可以准确地计算出路径效应,从而使得从微震记录数据中扣除路径影响及仪器记录引起的波形畸变,进而分离出震源信息成为可能。
矩张量是对震源处等效应力的一种近似表示,通过对该等效应力与震源模型(如断层滑移模型,内爆型岩体变形和岩体体积膨胀变形等)的比较,确定震源处岩体的破坏机理。当使用地震矩张量来表征震源时,通过实测波形与理论波形的拟合,迭代确定最优的震源模型。
首先依据定量地震学理论计算假设震源参数下传感器位置的理论波形及其幅度谱。比较该理论幅度谱与实测波形的理论谱,并计算二者之间的不拟合度(M):
2022年第4期/第43卷 采矿工程采矿工程 黄 金
M=∑i(usyni-uobsi)2∑i(uobsi)2(1)C27037F3-CB87-4007-87C0-DB3D95C9EE0D
式中:usyni为理论波形幅度谱第i采样点的幅值;uobsi为实测波形幅度谱第i采样点的幅值。
同时计算相对不拟合度(RM):
RM=M-BMBM(2)
式中:BM为最优解时的不拟合度(相对于每一个需要求解的震源参数)。
由式(2)可知,相对不拟合度为正值,当相对不拟合度接近零时,反演得到理论最优解,同时相对不拟合度也是评价反演是否稳定的一个重要指标。
2.1 频域波形拟合
根据上述不拟合度,应用Levenberg-Marquardt方法进行迭代计算,计算过程如图4所示。在频域内的反演将首先假设震源为双力偶模型,确定反演包括走向、倾角、滑移角、标量地震矩和震级在内的震源参数;然后计算在全波形矩张量反演下的震源矩张量元素及其分解结果,如图5所示。
2.2 时域波形拟合
频域拟合反演结束后,为消除P-T轴的不确定性,进行时域波形拟合的反演计算。在时域进行反演时,使用与频域反演时相同的数据斜坡化和带通滤波器参数。为进一步提高震源位置的精度,在进行时域波形拟合时,在频域计算结果的基础上,在该震源周围搜寻其他可能的震源位置,通过比较时域内的波形,确定最终震源位置,如图6所示。
3 工程应用
某地下铁矿是世界上最大的地下开采矿山之一,矿体走向长约4 km,厚度约80 m,矿体倾角约60°。随着采矿活动向深部发展,该矿山自2007年起微震活动增多,当前采矿活动主要集中于1 022~1 079 m,相对地表深度为785~845 m。矿山开采范围内正在运行的微震监测传感器共204个,其中87个为三分量传感器,这些传感器分为4.5 Hz和14 Hz 2種。
根据该矿山现场安全监测的需求,选取33个采场范围内的1次微震事件进行矩张量反演和震源机制分析,微震事件的基本震源参数如表1所示(该数据由IMS微震监测系统提供)。
在矩张量反演过程中需要使用带通滤波器对波形进行滤波处理,尤其是在频域拟合中,为尽量多地拟合频谱曲线的平滑部分,需要使带通滤波器越低越好,同时也要兼顾数据本身的准确度,因此所使用的带通滤波器的低频部分需要大于传感器的自振频率。鉴于该矿山微震监测传感器的自振频率均低于或等于14 Hz,因此本文将采用的带通滤波器的低频部分设置为15 Hz。
如上所述,考虑到需要尽量多地拟合频谱曲线的平滑部分,则所使用的带通滤波器的高频部分不能大于该事件的拐角频率,该微震事件的最低拐角频率为71.7 Hz(如表1所示),因此本文将带通滤波器的高频部分上限设为35 Hz。
为探寻最适合该矿山微震事件的带通滤波器,本文将在下列范围内逐一进行矩张量反演:15~20 Hz、15~25 Hz、15~30 Hz、15~35 Hz、18~25 Hz、18~30 Hz、18~35 Hz、21~25 Hz、21~30 Hz、21~35 Hz、24~30 Hz和24~35 Hz。
在矩张量反演过程中,仅带通滤波器这一唯一变量,其他影响因素的参数值保持固定。其中,全波形矩张量反演的时间窗长度为0.5 s,该时间窗开始于P波到时前0.2 s。断层面走向角度按5° 间隔从0°~360°迭代,断层面倾角按5° 间隔从0°~90°迭代,滑移角按5°间隔从-180°~180°迭代。
该矩张量反演依次在频域和时域内进行,均进行双力偶点源模型反演和全波形矩张量反演,频域和时域均采用相同的带通滤波器。
反演所用格林函数速度模型为:P波波速vP=5 500 m/s,S波波速vS=3 107 m/s,其在水平方向和竖直方向的空间采样率均为10 m,时间采样率为200 Hz,该格林函数数据库允许计算最大震源深度500 m,最大震中距5 000 m范围内的位移场。不同带通滤波器下的全波形矩张量反演结果及其分解所得的双力偶震源机制如图7所示。
由图7可知:事件在15~30 Hz带通滤波器下频域拟合反演稳定,断层面走向-倾角-滑移角及其不拟合度曲线在最优解两侧均匀分布,且15~30 Hz带通滤波器带宽较大,此时的不拟合度较小,因此15~30 Hz可作为最可靠的带通滤波器。同时,在不同带通滤波器下反演所得的全波形矩张量分解出的双力偶断层面解是一致的,均以剪切为主。
4 结 语
本文针对某铁矿微震事件频发、岩体垮落严重、支护系统破坏等问题,采用了一种新的包含频域拟合和时域拟合的全波形矩张量反演方法,旨在探寻适合该矿山三维监测网络下的微震事件矩张量反演方法,确保该方法能够快速计算矿山微震事件的矩张量参数及断层面解,计算结果与双力偶断层面解一致。
[参 考 文 献]
[1] GIBOWICZ S J,KIJKO A.An introduction to mining seismology[M].San Diego:Academic Press,1994:15-46.
[2] HASEGAWA H S,WETMILLER R J,GENDZWILL D J.Induced seismicity in mines in Canada—An overview[J].Pure and Applied Geophysics,1989,129(2):423-453.
[3] ORTLEPP W D.Invited lecture:the design of support for the containment of rockburst damage in tunnels—An engineering approach[C]∥KAISER P K,MCCREATH D R.Proceedings of rock support and underground construction.Rotterdam:Balkema,1992:593-609.C27037F3-CB87-4007-87C0-DB3D95C9EE0D
[4] LYNCH R A,WUITE R,SMITH B S,et al.Microseismic monitoring of openpit slopes[C]∥POTVIN Y,HUDYMA M R.Controlling seismic risk-rockbursts and seismicity in mines.Perth:Australian Centre for Geomechanics,2005:581-592.
[5] TRIFU C I,URBANCIC T I.Fracture mechanism for earthquakes:observations based on mining induced seismicity[J].Tectonophy-sics,1996,261(3):193-207.
[6] ANDRIEUX P P,SIMSER B P.Ground stability-based mine design guidelines at Brunswick Mine[C]∥HUSTRULID W A,BULLOCK R L.Underground mining methods hand book.Littleton:Society for Mining,Metallurgy and Exploration,2001:207-214.
[7] HEDLEY G F.Rockburst handbook for ontario hardrock mines[M].Canmet:Special Report,1992:296-305.
[8] MARTIN R H.Analysis and interpretation of clusters of seismic events in mines[D].Crawley:University of Western Austrlia,2008.
[9] 曹安業.采动煤岩冲击破裂的震动效应及其应用研究[D].徐州:中国矿业大学,2009.
[10] RIE K,NORI N,DAVID L.Introduction to microseismic source mechanisms[J].The Leadinge Dge,2015,8(1):875-880.
Fully waveform moment tensor inversion method and
its application to mine micro-seismic monitoring
Jian Zheng1,Ma Ju1,Liu Xiao2,Yong Guodong2
(1.School of Resources and Safety Engineering,Central South University;
2.Shandong Jinzhou Mining Group Co.,Ltd.)
Abstract:Passive monitoring techniques and source localization techniques for micro-seismic events have greatly improved the understanding of rock mass rupture and fault activity.In light of frequent micro-seismic events and severe rock body caving in a mine,a new fully waveform moment tensor inversion route incorporating frequency-domain fitting and time-domain fitting is used to seek the suitable moment tensor inversion method for the three-dimensional monitor-ing network of this mine,which ensures that the moment tensor parameters and fault solutions of mine micro-seismic events can be rapidly calculated,and that the moment tensor can be quickly decomposed and the fracture types of rock mass can be identified.According to the calculations,the dual force even fault facet solutions from the full moment tensor decomposition obtained by the inversion under different filters are consistent and all of them are shear-dominated.
Keywords:micro-seismic monitoring;fully waveform;moment tensor;inversion;shearC27037F3-CB87-4007-87C0-DB3D95C9EE0D
