南水北调工程陶岔站时差法流量计推流技术研究

邓山 赵昕 张莉 吴琼 左建

摘要：陶岔水文站为南水北调中线工程源头陶岔渠首水量计量断面，为提高陶岔站超声波时差法流量计的流量测验精度，对时差法流量计算原理及推流方法进行了研究，提出了基于多元回归的多声路时差法断面平均流速计算方法，并以实测流量为率定样本，验证了该方法的适用性。同时，基于走航式ADCP测验资料，分析了陶岔站垂线流速分布规律及最优幂指数，以及幂指数对ADCP流量测验精度的影响。结果表明：基于多元回归的多声路时差法断面平均流速计算方法能进一步提高陶岔站流量监测的精度;陶岔站垂线流速分布符合冪函数分布，最优幂指数为0.120 8，在用走航式ADCP进行流量测验时，建议采用该系数，可减小单次流量测验误差1%～2%。研究成果可为流量在线监测推流方法的选择及推流精度的提高提供参考。

关 键 词：流量在线监测; 超声波时差法; 流速分布; 多元回归; 陶岔水文站; 南水北调工程

中图法分类号： P332

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.04.014

0 引 言

南水北调工程是实现中国水资源优化配置，促进经济社会可持续发展，保障和改善民生的重大战略性基础工程。陶岔渠首枢纽工程是南水北调中线输水总干渠的渠首引水工程，其设计流量为350 m3/s，加大流量可达420 m3/s[1]。

随着南水北调中线工程的正式运行，对水量的配置、监控、调度、管理和考核提出了更高要求。水量的精确计量不仅关系到工程的运行管理，也决定着沿线城市用水管理的精细化程度。目前，常规的流量测验方法主要有转子式流速仪、走航式ADCP等，测验精度高，但人工工作强度大、间隔时间长，无法实现实时、在线监测。为此，在渠首工程闸下1+400 m处的陶岔水文站，安装了四声路超声波时差法流量计，实现了流量在线监测，为南水北调中线工程引调水控制、计量提供了精确的数据支撑。

由于时差法流量计实际测得的是流速，如何将流速转化为流量是关键也是难点所在，涉及到比测方案及代表流速关系的建立。目前，国内对超声波时差法流量计的研究主要集中在管道测流方面[2-3]，在明渠上的应用研究及流量计算方法的研究较少。王慧[4]研究了小波变化与傅里叶变换对时差法数据处理的效果，刘正伟等[5]

研究了时差法在牛栏江-滇池补水工程中的应用，韩继伟等[6]

研究了虚拟垂线流速时差法流量计算方法，赵德友[7]

研究了运河水文站流量自动监测系统建立与实现技术。但是关于时差法流量计算原理、比测方案本身的精度及代表流速关系拟合方法的研究相对较少。基于此，本文对时差法测流原理、流量计算方法等进行了详细阐述，提出了基于多元回归的多声路时差法断面平均流速计算方法;然后，以陶岔站为例，以实测流量为率定样本，分析了陶岔站超声波时差法测验精度及该方法的适用性;同时，研究了陶岔站垂线流速分布规律，计算了幂函数流速分布指数，以及幂指数对该站ADCP流量测验精度的影响。研究成果可为明渠及河道流量在线监测推流方法的选择及测流精度的提高提供参考。

1 原理及方法

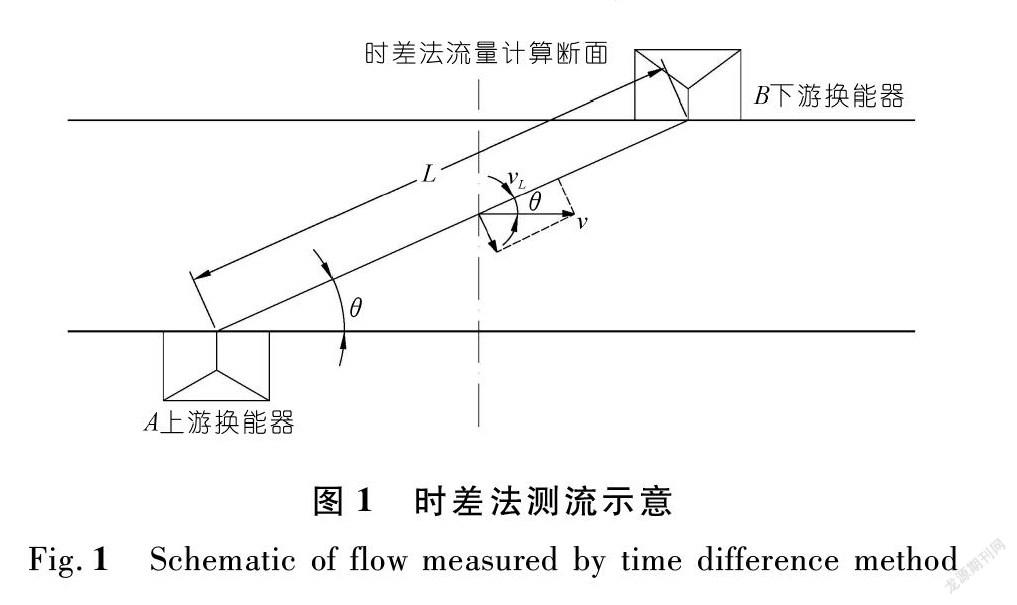
1.1 时差法测流原理

超声波时差法流量计是利用声波传播的特性，基于流速面积法原理制造出的测流仪器，其常规布置方法如图1所示。在河流两岸水下A、B处安装一对换能器，其距离为L，声波顺水流传播时，实际传播速度为声速c加上水流速度在AB方向的分量vL，传播时间T1=Lc+vL;逆水传播时，实际传播速度为声速c减去水流流速分量vL，传播时间T2=Lc-vL。

测出声波顺水和逆水传播的时间差就能测得水流速度，如式（1）～（2）所示。

vL=L2（1T1-1T2） （1）

v=vLcosθ=L2cosθ（1T1-1T2） （2）

1.2 时差法流量计算原理

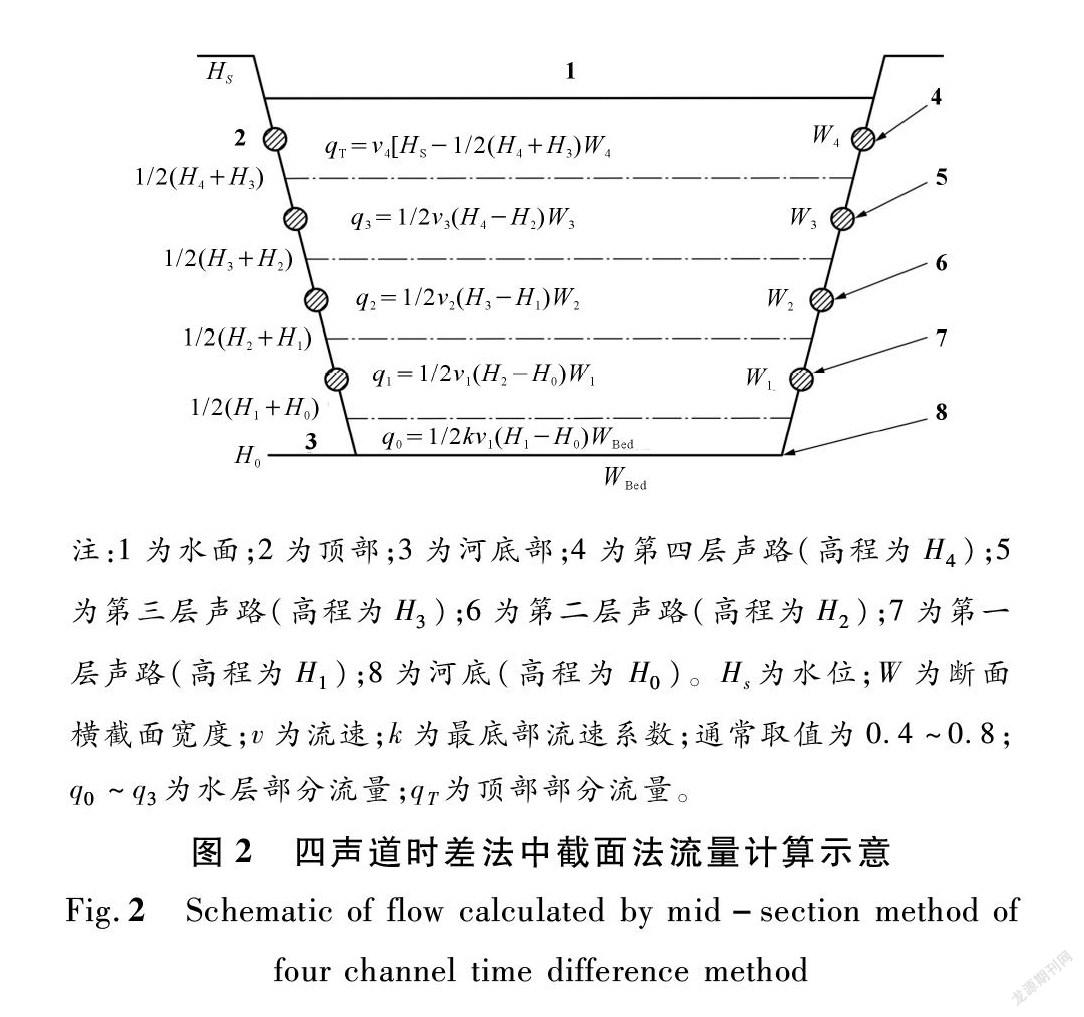
时差法是采用流速面积法计算流量，分为单声路系统和多声路系统。陶岔水文站采用的是四声路系统，其流量计算方法主要有中截面法和平均截面法[8]，两方法计算原理类似，其中中截面法计算示意如图2所示。由图2，可计算总流量q为

q=q0+q1+q2+q3+qT（3）

注：1为水面;2为顶部;3为河底部;4为第四层声路（高程为H4）;5为第三层声路（高程为H3）;6为第二层声路（高程为H2）;7为第一层声路（高程为H1）;8为河底（高程为H0）。Hs为水位;W为断面横截面宽度;v为流速;k为最底部流速系数;通常取值为0.4～0.8;q0～q3为水层部分流量;qT为顶部部分流量。

时差法系统可自行设置经验系数k，故最终流量为

Q=kq （4）

1.3 基于多元回归的关系拟合方法

时差法测流系统默认的算法通常情况下能测出较为可靠的流量数据，但也存在系数经验性较强，部分情况下测流精度不高等问题。因此，本文提出了基于多元回归的多声路时差法断面平均流速计算方法，通过实测流量计算出断面平均流速，与时差法测得的四层流速建立多元回归关系，再用此关系推算实时流量[9]。

断面平均流速与时差法流速关系拟合公式如下：

v平=a1v1+a2v2+a3v3+a4v4+b （5）

式中：v平为断面平均流速，v1～v4为时差法各水层流速。

考虑水文测验的数据特点，拟合时采用相对误差平方和最小为损失函数，即：

fx=min{ni=1xi′-xixi2} （6）

式中：xi′为拟合值，xi为实测值。

1.4 垂线流速分布规律

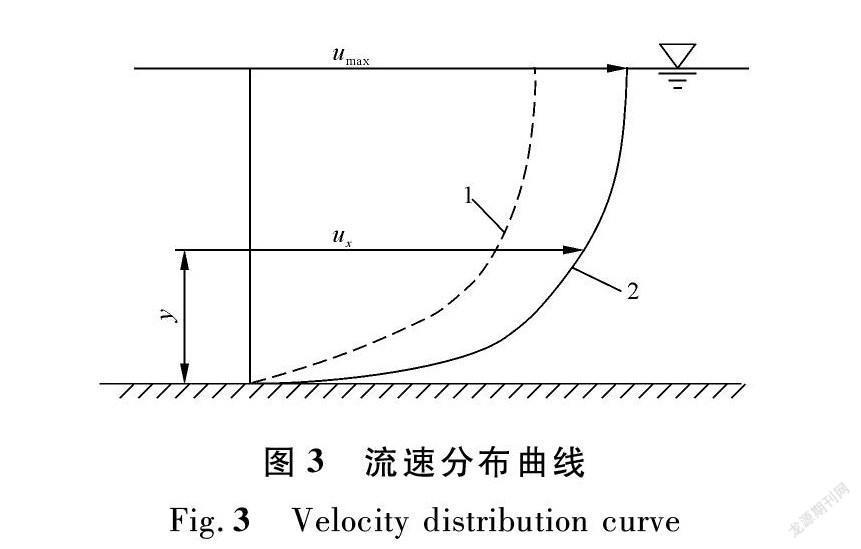
天然河道中的垂线流速常有一定的规律，一般水面流速大于河底，且呈一定的形状。许多学者经过试验研究导出了一些经验、半经验的模型，如抛物线模型、幂函数模型、双曲线模型、椭圆模型及对数模型等[10-11]。在大量水文测验的实践中发现幂函数流速分布与天然河道的垂线流速分布情况最为接近，且应用最广。幂函数公式如下：

uxumax=yr0b（7）

式中：b为指数，其值与雷诺数有关，对于明渠，b常取为1/5～1/8;ux为任意一点的流速;umax为垂线最大流速;r0为水深（见图3）。

在采用走航式ADCP进行流量测验时，在断面的顶部、底部和岸边会存在盲区，只能依靠关系系数进行推算。其中顶部、底部盲区一般采用幂函数关系，默认幂指数为0.166 7。若不进行垂线流速分布规律分析，会带来一定的插补误差，影响ADCP流量测验精度。因此，本文利用陶岔站实测ADCP流量数据对该站垂线流速分布规律进行了研究，并计算了优化指数对流量的影响。

2 应用实例

2.1 陶岔水文站测验情况

陶岔水文站为南水北调中线工程水情控制基本水文站，始建于2002年8月，位于河南省淅川县九重乡陶岔村，2014年1月1日下迁340 m，至渠首闸上140 m。为做好陶岔渠首水情控制、水资源监督管理服务等任务，2019年6月将测流断面迁至闸下1+400 m处，建设了水位、流量、雨量等水文测报设施，架设水文缆道1座、安装超声波时差法流量计1套。

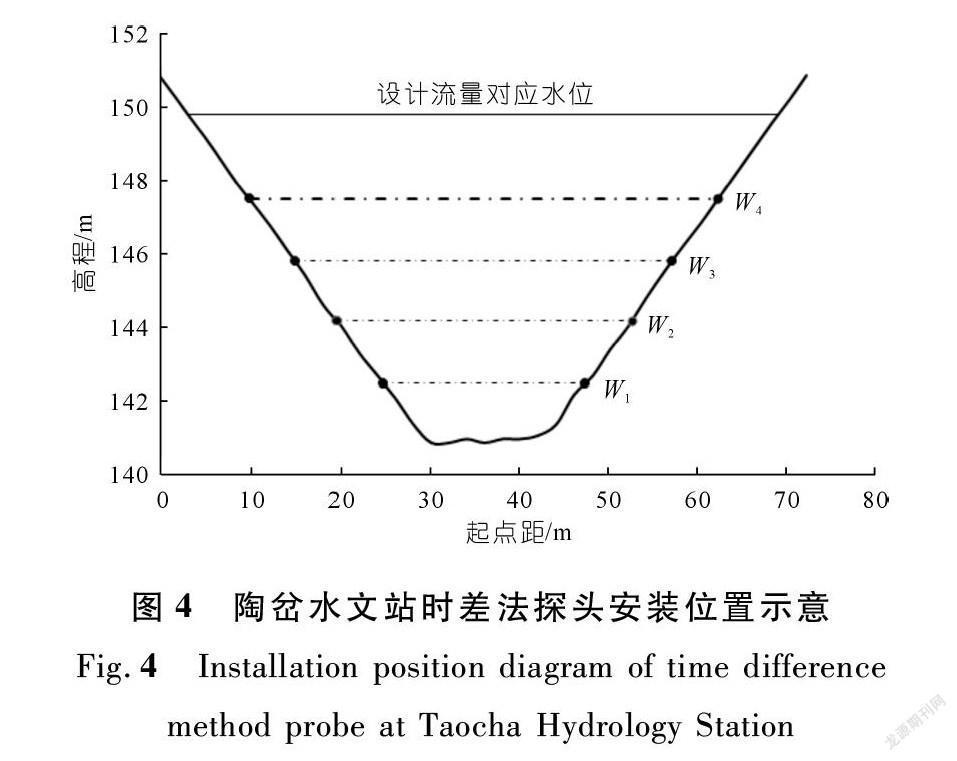
陶岔水文站时差法测流系统为德国Quantum有线时差法系统，采用四层换能器系统。根据断面及实测流量资料分析[12]确定四层换能器的安装高程（见图4）分别为142.5，144.2，145.8，147.5 m。于2019年10月完成调试，投入运行。

采用转子式流速仪法和走航式ADCP法进行比测，比测时间为2019年10月26日至2020年5月27日，共收集实测流量35次，其中流速仪法8次，走航式ADCP法27次。比测范围172～420 m3/s，基本涵盖了陶岔站输水量级范围，资料代表性较好。

2.2 关系拟合方案制定

（1） 断面面积计算。

由于测流断面与时差法流量计算断面往往并不重合，同时走航式ADCP法存在航迹线不是严格直线、盲区插补误差以及ADCP本身的测深误差等，这些都会导致面积测量存在误差，造成ADCP测得断面面积与时差法采用的断面面积不一致，经分析计算，陶岔站这种面积误差为2%～3%。由于陶岔站位于南水北调工程输水渠道，河段为固化渠道、无冲淤变化，断面稳定，且水文站定期实测大断面，故分析时应统一采用水位查大断面计算断面面积，以消除断面面积不一致带来的流量计算误差。

（2） 断面平均流速计算。

按照规范要求对实测流量资料进行处理，计算出实测流量。实测流量除以时差法计算的断面面积得到断面平均流速：

v-=Q实测/A时差法（8）

（3） 时差法分层流速处理。

将每次测流时间内的时差法流量计测得的各层流速分别进行平均，得到相应的平均流速v-1，v-2，v-3，v-4。

（4） 进行关系拟合。

将断面平均流速和对应的时差法分层流速按照公式（5）进行关系拟合，采用非线性规划进行求解。为防止过拟合，本次随机挑选27组数据进行拟合，预留8组数据进行检验。

2.3 结果分析

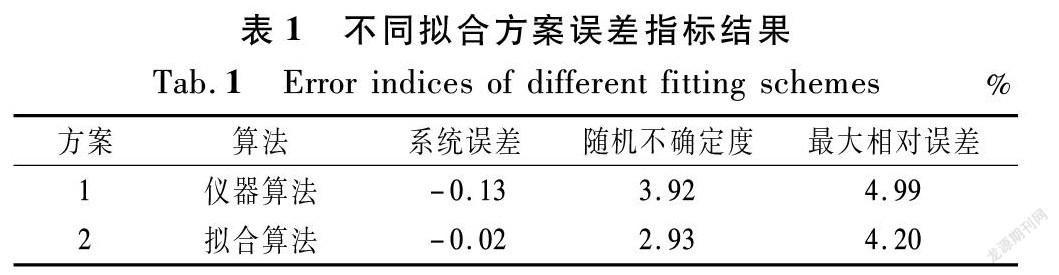
（1） 拟合精度评价。按照制定的方案进行关系拟合，计算出的拟合结果如式（9）所示，具体拟合计算误差统计结果如表1所列。

v平=0.013v1+0.265v2+0.67v4-0.05（9）

从表1可以看出，时差法流量计的精度较高，采用本文提出的拟合方法能进一步降低流量计算的系统误差及随机不确定度，单次流量推算误差均在±4.2%以内，能有效提高流量测验精度。

（2） 成果检验。

本次研究随机预留了8组数据作为检验样本，检验结果如表2所列。结果表明：本文提出的拟合方案检验误差均不超过3.0%，整体精度优于仪器自带方案，能够满足水文测验精度要求。

（3） 流量过程推求。

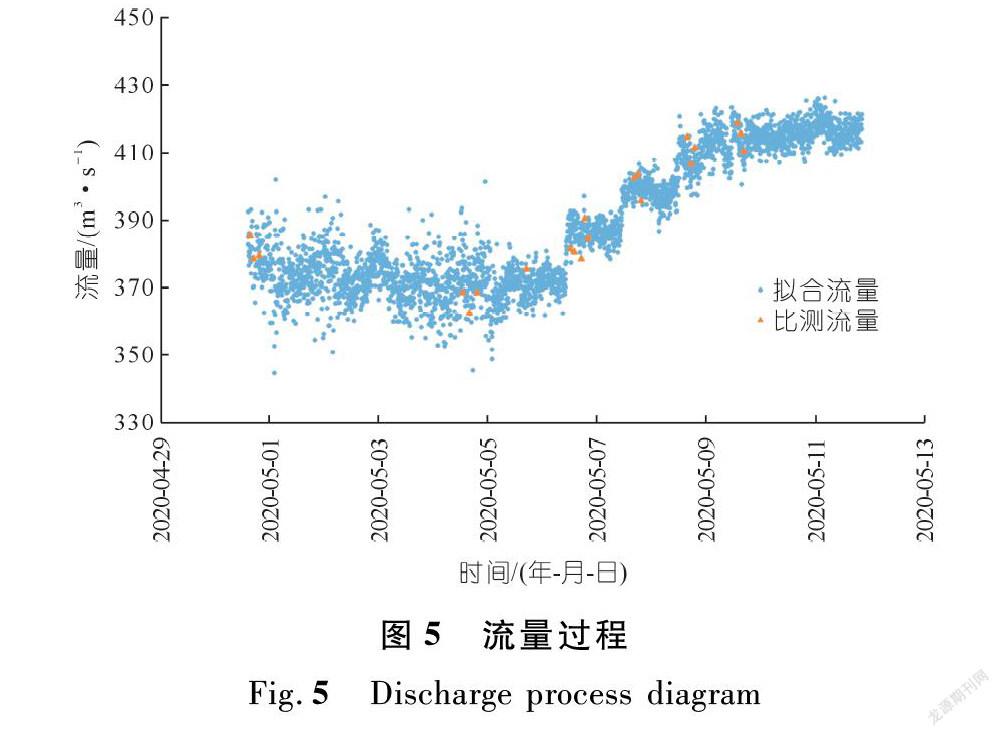
采用断面平均流速拟合公式（9），结合断面数据，计算出2020年5月1日至12日每5 min的流量过程，如图5所示。

从图5可以看出，虽然由于水流紊动影响，5 min流量存在一定程度的跳动，但流量过程合理，与比测流量吻合程度较好，表明推算的流量精度较高。

2.4 垂线流速分布規律研究

提取出各次ADCP测验成果的点流速数据，计算相对水深和流速，通过重心拟合分布曲线，计算出拟合程度最好的幂指数[13-14]，各测次拟合结果如表3所列。

以各次拟合幂指数的均值0.120 8作为陶岔站垂线流速拟合的幂指数。经对比，ADCP流量计算时，幂指数0.120 8与默认幂指数0.166 7推算的流量值两者之差约占总流量的1%～2%。为提高流量测验精度，建议陶岔站用ADCP进行流量测验时，将幂指数设置为0.120 8，并定期进行分析验证。

3 结 论

本文对超声波时差法的测流原理、流量计算方法进行了研究，在常规流量计算方法的基础上，提出了基于多元回归的多声路时差法断面平均流速及流量计算方法;然后以陶岔站为例，制定了其代表流速关系拟合方案，分析了其拟合精度及推流精度，并研究了陶岔站的垂线流速分布规律，计算了最优幂指数及其对流量大小的影响，得到如下结论。

（1） 在用ADCP进行超声波时差法比测率定时，应注意两者所用断面面积的一致性，对于固化渠道，定期测验大断面的前提下，建议分析时统一采用水位查大断面计算断面面积，以减小断面不一致带来的流量计算误差。

（2） 本文提出的基于多元回归的多声路时差法断面平均流速计算方法能进一步提高陶岔站流量监测的精度，满足南水北调工程水量计量的要求。该方法可作为时差法等在线监测设备的代表流速关系拟合方法，相比传统的线性拟合方法能较明显地提高拟合精度，具有较大的实用价值。

（3） 陶岔站垂線流速分布符合幂函数分布，幂指数为0.120 8，在用走航式ADCP进行流量测验时，建议采用该系数，可减小单次流量测验误差约1%～2%，在进行流量测验时应采用分析计算值。

研究成果可为超声波时差法流量在线监测应用中代表流速关系的拟合计算提供参考，对于人工渠道及天然河道的流量在线监测均有一定的应用价值。

参考文献：

[1] 张娜，胡石华，曾思栋，等.南水北调中线扩大供水满足二期需求可能性研究[J].人民长江，2015，46（增2）：39-41.

[2] 贾惠芹，王成云，党瑞荣.流体流速对超声波流量测量精度的影响及校准[J].仪器仪表学报，2020，41（7）：1-8.

[3] 杜晓泽，刘胜祥.时差法超声波流量计流量系数影响因素分析[J].工业计量，2019，29（2）：14-15，38.

[4] 王慧.时差法超声波流量计数据处理方法的研究[D].大连：大连理工大学，2010.

[5] 刘正伟，张丽花.超声波时差法在流量自动监测中的应用：以牛栏江-滇池补水工程为例[J].人民长江，2016，47（增1）：53-55.

[6] 韩继伟，牛睿平，王岩，等.虚拟垂线流速时差法流量计算方法研究[J].水文，2020，40（1）：52-57.

[7] 赵德友.运河水文站流量自动监测系统建立与实现技术[J].水利信息化，2011（3）：68-72.

[8] Hydrometry-Measurement of discharge by the ultrasonic transit time （time of flight） method：ISO 6416[S].BSI Standards Publication，2017.

[9] 邓山，胡立，左建，等.H-ADCP代表流速与断面平均流速拟合精度研究[J].人民长江，2020，51（10）：100-104.

[10] 张坤军，张杰，王佑喜，等.ADCP盲区流速反演模型在钱塘江河口地区的应用[J].人民长江，2017，48（增1）：117-119，151.

[11] 陆虹，胡进华，韩松林.引水明渠二维水流数学模型的建立及应用[J].人民长江，2016，47（22）：98-101.

[12] 刘东生，左建，林云发，等.南水北调中线陶岔渠首段流速分布规律研究[J].水利水电快报，2019，40（1）：48-52.

[13] HUANG H.Estimation of type a uncertainty of moving-boat ADCP streamflow measurements[C]∥River Flow，2016.

[14] MUELLER D S.Extrap：software to assist the selection of extrapolation methods for moving-boat ADCP streamflow measurements[J].Computers & Geosciences，2013，54：211-218.

（编辑：谢玲娴）

Research on discharge calculation by ultrasonic transit time method flowmeter at Taocha

Hydrological Station，canal head of South-to-North Water Diversion Project

DENG Shan1，ZHAO Xin1，ZHANG Li1，WU Qiong1，ZUO Jian2

（1.Bureau of Hydrology，Changjiang Water Resource Commission，Wuhan 430010，China; 2.Hanjiang Hydrology and Water Resources Survey Bureau，Hydrology Burean of Changjiang Water Resources Commission，Xiangyang 441000，China）

Abstract：

Taocha Hydrological Station is the flow measurement section of Taocha canal head，which is the source of Middle Route of South-to-North Water Diversion Project.In order to improve the accuracy of ultrasonic transit time method flowmeter，this paper studied the principle and method of discharge calculation，and put forward the average velocity calculation method of multi-layer transit time method based on multiple regression.The applicability of the method was verified by using the measured discharge as a calibration sample.At the same time，based on the ADCP measurement data，optimal power index of vertical velocity distribution at Taocha Station and its influence on the accuracy of ADCP discharge measurement were analyzed.The results show that the average velocity calculation method of multi-layer transit time method based on multiple regression can improve the accuracy of discharge monitoring at Taocha Station.The vertical velocity distribution at Taocha Station conforms to power function distribution，and the optimal index is 0.1208.It is recommended to use this coefficient when using the navigation ADCP for discharge measurement，which can reduce the error of a single discharge measurement by 1% to 2%.The research results can provide reference for the selection of discharge calculation methods for online discharge monitoring and the improvement of discharge calculation accuracy.

Key words：

discharge online monitoring;ultrasonic transit time method;velocity distribution;multiple regression;Taocha Hydrological Station;South-to-North Water Diversion Project