基于爬山—蚁群—FCM模糊聚类的不良负荷数据辨识

甘迪, 金岩磊, 葛立青，郭鑫溢

(南京南瑞继保电气有限公司，江苏 南京 211100)

近年来，随着我国大力建设智能电网，电力系统涌入了海量的实时数据[1-3]。负荷数据与负荷预测、电力系统状态估计息息相关，但数据测量、传输等环节出现的偶发故障和干扰，使得电力系统出现了与实际值偏差较大的不良负荷数据，干扰电力调度的决策，威胁电力系统的安全稳定运行。有效不良负荷数据辨识有助于提高电力系统分析计算准确度，提升智能用电水平和电网的安全性。

目前数据辨识领域的研究成果较多。文献[4]采用空间密度聚类和异常数据域方法进行负荷异常值识别。文献[5]引入小波阈值去噪和多维核密度估计解决类噪声辨识问题。文献[6]针对风电次同步振荡参数辨识问题，采用加阻尼Rife-Vincent 窗和三点插值法计算复数域下的参数指标并进行参数辨识。文献[7]基于最大测点正常和CPU并行加速，提出一种不良数据辨识模型。在数据辨识研究中，模糊聚类算法[8-10]是解决不良负荷数据辨识的有效方法之一，但通常存在以下方面的不足：(1)聚类数量和聚类中心选取具有偶然性，二者严重影响着聚类性能；(2)需要权衡算法效率和算法质量；(3)由于用电数据规模庞大，目标函数容易陷入局部最优[11]。为克服以上问题，本文尝试将启发式算法[12]与元启发式算法[13]相结合，以FCM聚类算法为基础，采用蚁群算法[14-15]确定FCM聚类算法的聚类数目、聚类中心，并由爬山算法[16]为蚁群算法提供初始解，求解聚类结果，计算负荷可行域上下限，当实际负荷超出可行域上下限时视为不良数据，并采用插值法[17]进行数据修复，实现电力不良数据辨识和修复的功能。

1 FCM负荷曲线聚类

负荷曲线聚类是指利用聚类算法对历史负荷数据进行分类，以数据为支撑，分析不同类型用户的负荷特性，为电力负荷预测、电价制定等提供决策依据[18-20]。FCM算法[21-22]是一种常见的聚类算法，使用隶属度衡量样本点的相似性，该算法可描述如下：

对含有n个样本的样本集，每一个样本都可以用一组特征向量表示，假设这些样本可以被分为c个聚类中心，则算法的目标函数是n个样本到其聚类中心的类内距离加权平方和最小，即

(1)

式中：U为模糊划分矩阵，V为聚类中心矩阵，m为加权指数，取值范围在[1,+∞]，uik为第k个样本属于第i类聚类中心的隶属度，dik为第i类样本中第k个样本到第i类聚类中心的距离。

隶属度[23]满足：

(2)

式(1)随着加权指数m单调递减，但存在拐点m0使得算法的迭代次数随m的取值呈现震荡变化的趋势，在拐点m0附近取到极小值，即：

(3)

依据拉格朗日乘数法，可以求得目标函数取极小值时，隶属度uik和聚类中心vi需满足：

(4)

(5)

以式(1)为目标函数，以式(2)(4)(5)为约束条件，当迭代一定次数后目标函数前后两次迭代误差小于一给定正数时，聚类结束。

2 蚁群算法

蚁群算法(ant colony algorithm, ACA)是一种模拟蚂蚁觅食行为的元启发式搜索算法，在没有任何提示的情况下，蚂蚁通过在路径上释放分泌物——信息素[24-25]，从而找到从巢穴到食物的最短路径。如果路径上出现意外，蚁群能够自适应地寻找到新的最优路径。蚁群算法的优势在于鲁棒性强、记忆性能好、易与其他优化算法相结合等，具有分布式计算、正反馈性、正组织性等特征[26-27]。

蚁群根据信息素和距离来搜索路径，在第t次迭代中，蚂蚁k由节点i选择下一节点j的转移概率满足：

(6)

(7)

式中：qij为路径(i,j)的信息素浓度。α为信息素启发因子，β为期望启发式因子，α越大算法搜索性越弱，β越大代表先验路径信息的作用越大，越接近贪心算法。allowk表示路径搜索下一可到达节点的集合，nij为启发信息，dij为节点i和待选节点j的欧氏距离。

在信息素更新方式的选择上，为提高蚁群算法的搜索效率，本文引入精英蚂蚁系统，该系统通过在当前最优解Tbest更新信息素时释放额外的信息素，实现增强系统正反馈作用的目的。相关信息素更新的计算公式为：

(8)

(9)

式中：w是调整最优解的参数，代表强化项的权重，Lbest是当前最优路径Tbest的长度。

本文引入蚁群算法用于模糊聚类过程中选取聚类数量和聚类中心，克服其偶然性，增大获得最优解的概率。

3 爬山算法

蚁群算法作为一种元启发式算法，其算法效果非常依赖初始解的质量，可以利用爬山算法为蚁群算法产生初始解，提高算法性能。爬山算法是一种寻优速度快的启发式局部搜索算法，从当前节点开始，与周围节点进行比较，若当前节点值最大，则返回当前节点作为“山峰最高点”，反之则用最高的周围节点替换当前节点，如此循环迭代直到到达最高点。

本文采用狼爬山算法为蚁群算法提供初始解，该算法是基于经典Q学习算法[28]框架的一种强化学习算法。设表征状态动作好坏的值函数Q(s,a)，则有：

(10)

(11)

式中：Vφ*(s)为最优目标值函数，φ*(s)为策略，A为动作集。Q函数的更新机制采用SARSA策略，即：

Qk+1(s,a)=Qk(s,a)+αδkek(s,a)

(12)

Qk+1(sk,ak)=Qk+1(sk,ak)+αρk

(13)

式中：α为Q学习率，δk为Q函数误差，ek为状态s在动作a下第k步迭代的资格迹，ρk为在第k步迭代的Q函数误差。随着迭代次数的增加，状态值函数Q(s,a)能够逐步收敛到最优联合动作策略。

狼爬山算法基于虚拟博弈，将Q学习率α视为随迭代动态更新的变量，采用近似均衡的平均贪婪策略，引入两个学习参数αwin和αlose代表智能体的赢和输。设智能体的混合策略集为U(sk,ak)，变学习率为φi，它将在奖励函数R的基础上执行动作ak，从状态sk过渡到sk+1，则其更新律为：

U(sk,ak)←U(sk,ak)+

(14)

(15)

式中：φlose>φwin,avg为平均策略混合值，当该值低于当前策略值时，智能体获胜，选择φwin，否则选择φlose。

然而，爬山算法容易陷入局部最优，形象的说法是爬山是在迷雾中攀爬，其迷雾缺陷如图1所示，如果从B点开始搜索，爬山算法会认为A点是最优解，而错过真正的最优解D；如果从C点开始搜索，则能够得到正确的答案。为解决迷雾缺陷，本文在狼爬山算法的基础上做如下改进：在一定程度上扩大初始状态空间，从更多的起点出发搜索，结果取所有“山峰最高点”的最大值。

图1 爬山算法迷雾缺陷示意图Fig.1 Schematic diagram of fog defect of hill climbing algorithm

4 不良数据辨识与修正

在获得负荷数据的模糊聚类结果后，提取负荷特征曲线为所有聚类中心的采样点连线，并结合聚类后的负荷曲线和特征曲线得到负荷数据可行域，步骤如下：

(1)对历史负荷数据集合M，针对第i种分类，求出该类数据在同一时刻的最大值和最小值，即：

(16)

(2)根据特征曲线vi，计算可行域的上下限，即：

(17)

式中：p为采样点的个数。

当采样点在可行域上下限范围内时，视为负荷数据正常；当超出可行域上下限范围时，视为不良负荷数据。

对不良负荷数据，本文采用插值法进行数据修正。

5 算法流程

本文提出了一种基于爬山-蚁群-FCM模糊聚类的电力不良负荷数据辨识方法，以FCM聚类算法为基础，由爬山算法为蚁群算法提供初始解，根据蚁群算法确定FCM聚类算法的聚类数目、聚类中心，并求解聚类结果。这样做可以将启发式算法与元启发式算法相结合，发挥各自优点，互补缺点，以克服局部最优问题，提高其性能；同时也解决了聚类数量和聚类中心选取具有偶然性的问题。在聚类结果的基础上，计算负荷可行域上下限，当实际负荷超出可行域上下限时视为不良数据，然后利用插值法进行数据修复，实现电力不良数据辨识和修复的功能。其算法流程如图2所示，步骤如下：

图2 算法流程图Fig.2 Algorithm flowchart

步骤1：导入样本数据，用爬山算法确定蚁群算法的初始解。

步骤2：根据初始解，采用蚁群算法确定FCM聚类算法的聚类数据和聚类中心，初始化隶属度矩阵。

步骤3：完成FCM聚类，提取负荷数据特征曲线。

步骤4；根据负荷数据特征曲线，训练生成负荷数据可行域区间。

步骤5：导入待测数据。

步骤6：对待测数据进行不良数据辨识。

步骤7：对不良数据进行修复。

6 算例分析

6.1 模型评价

为验证模型的有效性，有必要建立模型的评价标准。聚类算法是为解决分类问题而提出的，首先应当对分类的准确性进行评价，在分类准确的基础上才做出修复准确的判定。因此，本文设某负荷数据点采集值偏离真实值超过20%为不良负荷数据，并采用精准率PRE、准确率ACC、召回率REC三项常见的分类问题评价指标来评价聚类效果指标，相关计算公式如下：

PRE=nTP/(nTP+nFP)

(18)

ACE=(nTP+nTN)/(nTP+nTN+nFN+nFP)

(19)

REC=nTP/(nTP+nFN)

(20)

式中：n为每类事件的数量，TP和TN均代表正确判别，FN代表漏判，FP代表误判，如表1所示。所有指标取值均在[0,1]之间，取值越大，聚类效果越佳。

表1 混淆矩阵Tab.1 Confusion matrix

在数据修复的模型评价上，则采用传统的平均误差率e评价模型。

6.2 算例有效性验证

本文以某市2020年3月某用电管理平台采集到的某用户电力负荷数据为算例数据，采样周期为15分钟，每天有96个采样点。同时收集该用户侧负荷数据作为真实数据，用于检验不良负荷数据辨识结果的正确性和精确性。

首先进行聚类分析，采用爬山算法和蚁群算法求解FCM聚类问题，以爬山算法为蚁群算法提供初始解，由蚁群算法提供FCM聚类算法的聚类数据和聚类中心。根据蚁群算法结果，初始的聚类中心为3个，聚类数据分别包含19、31、35个样本点，取加权指数m=3计算新聚类中心，不断迭代直到满足退出条件，获取聚类结果。

根据聚类结果计算特征曲线和可行域上下限，辨识不良负荷数据，并对不良负荷数据采用插值法进行数据修正。其结果如表2和表3所示。

表2 不良负荷数据辨识结果Tab.2 Identification result of bad load data

表3 不良负荷数据辨识模型评价Tab.3 Evaluation of bad load data identification model

表2中不良数据点号是指从3月1日0点开始记为1号点，0点15分记为2号点，以此类推。由表2可以推出以下结论：

(1)在3月用电管理平台采集到的负荷数据中，根据经验常识，一共出现了2次真实发生的、偏差较大的不良负荷数据，一次是182号点，该点采集值是791.2，真实值是320.6，采集值偏离真实值达到146.8%，按照负荷数据点采集值偏离真实值超过20%视为不良负荷数据的判断标准，该点属于不良数据，本文方法在该点判别上正确，修正值为329.5，修正值偏离真实值为2.8%，按照经验来看修正有效。

(2)第2个不良数据点是1539号点，该点采集值是593.3，真实值是389.2，采集值偏离真实值达到52.4%，按照负荷数据点采集值偏离真实值超过20%视为不良负荷数据的判断标准，该点属于不良数据，本文方法在该点判别上正确，修正值为411.4，修正值偏离真实值为5.7%，按照经验来看修正有效。

(3)本文方法没有对其他非不良数据点造成误判，即FP=0；对所有的不良数据点均正确判别，没有错判，即FN=0；本文方法在本算例的识别效果验证了方法的准确性和有效性。

表3列举了本文算法的聚类效果评价指标值。由表3可以看出，本文算法的PRE、ACE、REC在这次算例中均为最佳值1，没有发生漏判，即出现未成功判断出某次不良数据的现象；也没有发生误判，即错误地将正常数据判定为不良数据。分析原始数据可知，这主要是因为选取的负荷数据质量好，绝大多数的数据偏差小于3%。由此可见，本文提出的爬山-蚁群-FCM聚类算法能够有效地在2976个负荷采样点中辨识出唯二的不良数据点，验证了模型的有效性。

作为对比，本文将蚁群-FCM聚类算法、爬山-FCM聚类算法应用到相同的算例中进行不良数据辨识，其结果如下表所示：

由表4可以分析得出以下结论：

表4 不同算法结果对比Tab.4 Comparison of results of different algorithms

(1)面对质量好的一段负荷数据样本，本文算法、蚁群-FCM聚类算法、爬山-FCM聚类算法都能够有效辨识不良数据，没有发生漏判和误判；

(2)对比算法的平均误差分别为5.31%和5.96%，均低于本文算法的4.25%，验证了本文模型的有效性和准确性。

6.3 算例鲁棒性验证

为进一步验证本文模型的鲁棒性和准确性，本文扩大数据范围，将该市从4月到12月共9个月(每个月取1号到30号数据)的电力负荷数据作为研究对象，每个月独立做聚类分析。由于实际采集中不良数据点数较少，本文人为将每月的1号到30号中，每天96个采样点的第10、20、30、40、50个点增大25%，第15、25、35、45、55个点减小25%，则每天共有10个不良数据点，每个月有300个不良数据点，合计2700个不良数据点，总数据点达25920个点。通过人为对部分真实负荷数据进行缩放，实现了制造更差负荷数据质量、更多不良负荷数据的目的，在这种环境下考察不良负荷数据辨识算法的鲁棒性。采用本文方法、蚁群-FCM聚类算法、爬山-FCM聚类算法对这些经过处理后的数据进行分析，各算法数据辨识对比分析结果如表5所示。

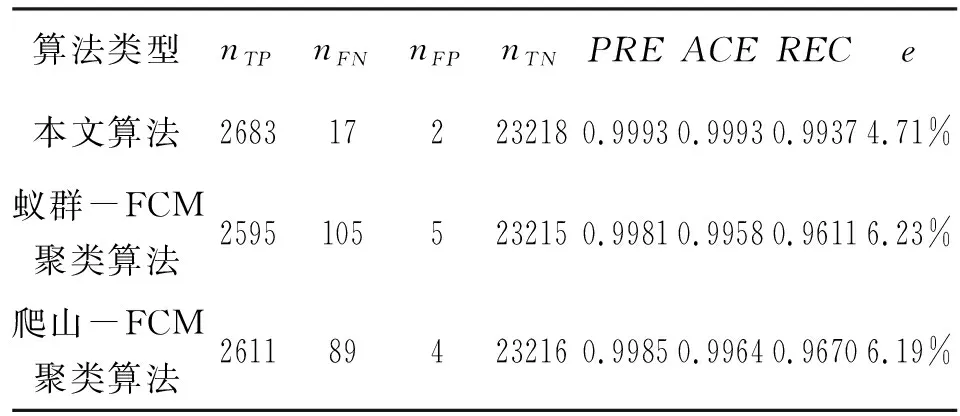
表5 不同算法鲁棒性结果对比Tab.5 Comparison of robustness results of different algorithms

由表5可以推出以下结论：

(1)本文方法在25920个负荷数据的不良数据辨识中，漏判了17个点，而蚁群-FCM聚类算法漏判105个点，爬山-FCM聚类算法漏判89个点，从漏判角度而言，本文方法优于蚁群-FCM聚类算法、爬山-FCM聚类算法。

(2)本文方法在25920个负荷数据的不良数据辨识中，错判了2个点，而蚁群-FCM聚类算法错判5个点，爬山-FCM聚类算法错判4个点，从错判角度而言，本文方法优于蚁群-FCM聚类算法、爬山-FCM聚类算法。

(3)本文方法的PRE为0.9993，优于蚁群-FCM聚类算法的0.9981，也优于爬山-FCM聚类算法的0.9985；同理，其余3项指标ACE、REC、e均优于蚁群-FCM聚类算法、爬山-FCM聚类算法。这说明面对样本数据规模大、突变率25%逼近20%分界线等难点，本文算法相比蚁群-FCM聚类算法、爬山-FCM聚类算法表现更优，鲁棒性和准确性更强。算例结果表明，本文提出的组合搜索算法能有效提高单一搜索算法的精度，验证了本文模型的鲁棒性和准确性，具有更好的工程实践优势。

7 结论

本文提出了一种基于爬山-蚁群-FCM模糊聚类算法，用于求解电力不良负荷数据辨识的问题。首先利用爬山算法为蚁群算法产生初始解，提高算法性能，接着用蚁群算法求解FCM负荷曲线聚类模型；根据聚类结果计算特征曲线和可行域上下限，辨识不良负荷数据，并对不良负荷数据采用插值法进行数据修正。算例表明，本文模型能够有效实现不良负荷数据辨识功能，在模型的准确性上相比单一搜索算法更优，可推广到其他电力采集数据的数据辨识等领域。但在实际应用过程中，不良数据的修正值和实际值之间仍然存在偏差，特别是对于罕见的负荷快速、剧烈波动的场景，偏差会进一步增大，如何解决这一问题，是下一步的研究方向。