柔性关节机械臂的自适应命令滤波输出反馈控制

目前,机械臂被广泛应用于工业、农业、医疗服务等领域,但是传统的机械臂都采用刚性结构,在机械臂操作过程中很难保证系统交互的安全性和可靠性。柔性关节驱动的机械臂能够提供良好的柔性行为,具有质量轻、灵活性好、能耗低、惯性小等优点,在航空航天、医疗康复等领域具有广阔的应用前景和发展潜力

。然而,柔性关节的引入使机械臂在运动过程中不可避免地会产生弹性振动,严重降低系统的控制精度。

针对柔性关节机械臂的控制问题,学者们提出了基于反馈线性化的控制

、奇异摄动

、滑模控制

、PID控制

、反步控制

等多种有效的控制方法。反步法由于设计步骤清晰且容易保证系统的稳定性,受到了学者们的广泛青睐,但是该方法需要对中间虚拟控制量进行反复求导,存在“计算爆炸”的问题。为此,文献[13-15]提出了基于动态面控制技术的反步设计法,避免了直接对虚拟控制量进行求导的繁琐过程。文献[16]和[17]提出了一种基于二阶命令滤波器的反步设计法,不同于动态面控制,它采用二阶滤波器,通过积分而非微分过程获得了虚拟控制量的导数,不仅避免了“计算爆炸”的问题,而且减少了测量噪声对控制系统的影响。文献[18]利用二阶命令滤波技术为

连杆柔性关节机器人设计了自适应模糊命令滤波控制器,实现了机械臂的高精度跟踪控制。文献[19]和[20]还引入误差补偿机制,消除了滤波误差对控制性能的影响。遗憾的是,这些文献需要全状态反馈信息,即要求机械臂角度和角速度均可测量,而在实际应用中,出于空间、重量、成本等因素的考虑,系统往往难以配备所有状态测量所需的传感器,因此基于全状态反馈的控制器便难以被应用。

针对机械臂部分状态不可测的情形,文献[21]设计了一种基于神经自适应观测器的动态面输出反馈控制器。文献[22]提出了一种基于等价输入干扰的鲁棒控制方法。文献[23]设计了一种扩展状态观测器用以对系统不可测量状态和模型匹配不确定性进行估计,并通过线性反馈补偿控制实现了柔关节机械臂的跟踪控制。文献[24]还进一步提出了一种基于级联扩展状态观测器的滑模控制方法,降低了观测器阶数,提高了控制系统的鲁棒性能。然而,这些方法大多依赖于系统精确的数学模型,并且需要跟踪误差的高阶求导,即把误差方程转化为线性化模型,当这种转换难以完成时,控制方法便无法实施。

近年来,借助于神经网络和模糊系统对非线性函数较强的逼近能力,众多学者研究了不确定系统的稳定控制问题。例如,文献[25-26]将RBF神经网络应用于无人机控制系统,对系统的不确定性和干扰进行了逼近和补偿控制。文献[27]利用函数逼近技术对柔性关节机械臂的非匹配不确定性进行了逼近,设计了自适应滑模控制器;文献[18]应用模糊系统对柔性关节机械臂的非线性项进行估计,设计了命令滤波反步控制器,但是它们未考虑未知外界干扰的影响。

基于上述分析,本文针对系统模型难以精确获得以及存在未知干扰的柔性关节机械臂,考虑机械臂部分状态不可测的情形,引入二阶命令滤波和神经网络逼近技术,提出一种基于自适应神经网络观测器的命令滤波反步跟踪控制方法,在避免控制算法出现“计算爆炸”的同时,实现机械臂高精度的输出反馈跟踪控制。具体地,将RBF神经网络和状态观测器相结合,通过自适应权值更新率推导,设计自适应神经网络观测器,用于对机械臂状态进行实时估计。然后,采用二阶命令滤波器反步设计法,通过RBF神经网络对模型不确定项的近似逼近,设计神经网络命令滤波反步跟踪控制器,并利用Lyapunov稳定性理论证明控制系统所有闭环信号的一致最终有界性。最后,给出对比仿真实例,验证所提方法的有效性和优越性。

与其他方法相比,所提方法具有以下优点:

:设计虚拟控制

实现

对期望轨迹

的跟踪控制。定义跟踪误差

=

-

,对

求导得

(2)控制算法通过积分而非微分的形式避免“计算爆炸”的问题,减小了不确定性因素对控制系统的影响;

(3)控制设计无需复杂的模型变换,避免了对跟踪误差进行高阶求导,使控制器结构更为简单。

1 系统建模与问题描述

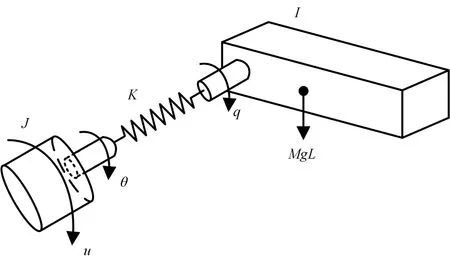
单连杆柔性关节机械臂是一个由柔性关节和刚性连杆组成的机电系统,其模型结构如图1所示。图中,参照文献[22]的坐标系定义方法,

为机械臂连杆相对于坐标系垂直轴的角度;

是驱动电机相对于坐标系垂直轴的转角;

、

、

分别是机械臂的质量、重力加速度、关节轴线到杆质心的距离;

为关节刚度;

、

分别为机械臂和电机的转动惯量;

为控制电机力矩输入。

本文研究机械臂存在不确定性影响下的跟踪控制问题,根据欧拉-拉格朗日原理,不确定柔性关节机械臂的动力学方程表示为

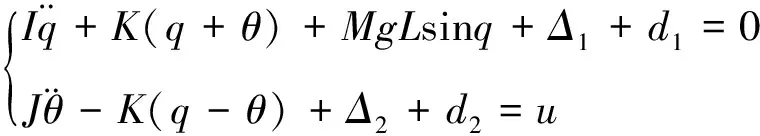
(1)

式中:

和

为外界干扰信号;

和

为包含参数摄动和未建模动态等模型不确定部分。

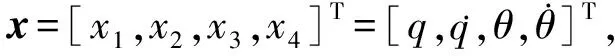
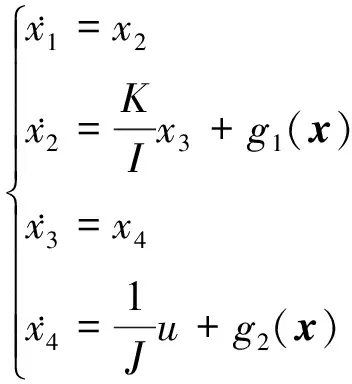
(2)

式中:

(

)和

(

)为以下形式的未知连续函数

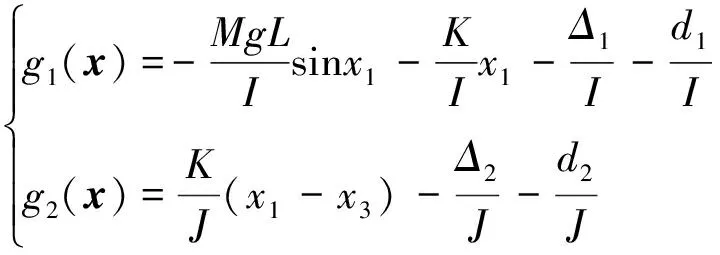
(3)

式中:

和

分别为理想权向量

和高斯函数

(

)的上限,满足‖

‖≤

,‖

(

)‖≤

。将式(17)代入式(16),整理可得

如果未知非线性函数

(

):

→

在紧集

上连续,那么存在RBF神经网络

(

),以任意精度对

(

)进行逼近,具体表达为

(

)=

(

)+

(4)

(5)

其中,

=[

1

,

2

,…,

]和

分别为高斯基函数的中心点向量和宽度。理想权值向量

一般是未知的,它可通过下式来计算

超分子化学根源于配位化学，分子印迹技术（MIT）属于超分子化学应用范畴[9]，其原理与“抗原-抗体”识别相似，主客体分子能够按“印迹模板”进行自识别、自组装、自组织与自复制作用，可阐明“分子社会”间相互作用，通常描述为“分子钥匙”的人工“锁”技术[10]。

(6)

二阶命令滤波器被定义为

(7)

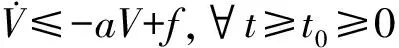
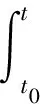
(8)

式中:

为任意常数。

外界干扰信号

和

是连续且有界的,即存在未知的正常数

和

,使外界干扰信号满足|

|≤

,|

|≤

,且其一阶导数连续且有界。

机械臂的期望轨迹

连续且一阶可导。

:设计虚拟控制

,使

收敛于0。由式(30)可得

2 自适应命令滤波输出反馈控制

本节给出基于RBF神经网络的状态观测器和命令滤波反步控制器的设计步骤。基于状态观测器的命令滤波反步控制系统结构框图如图3所示。

2.1 自适应神经网络观测器设计

实际应用中,柔性关节机械臂往往仅在连杆上配备角度传感器以降低系统成本和提高系统结构紧凑性,此时连杆的角速度以及电机轴的转角位置和角速度等状态便难以获取。为此,本节设计一种基于自适应神经网络的状态观测器,以实现对状态变量

、

和

的实时估计。

首先,将式(2)整理为

(9)

式中:

(

)=[0,

(

),0,

(

)]

;

为Hurwitz矩阵;

为输入矩阵;

为输出矩阵,且(

,

)可观测。定义

(

,

)=

u

(

)+

(

),则式(9)可表达为

(10)

由于

(

,

)中的

(

)是包含状态变量

和

以及未知不确定性的非线性函数,假设

(

,

)未知,则根据引理1,可利用RBF神经网络对其进行逼近,即

再次，信贷风险内部审计是强化职业道德建设、防范道德风险的有力保障。由于农村环境复杂，各种利益交互，各种势力纵横，各种利益共同体都在谋求自身利益。在逐利的道路上，这些群体由于自有资金不足而受阻。农村金融市场竞争不充分，地下高利贷市场资金利率较高，这些人纷纷将期许的眼光投向新设立的村镇银行。而村镇银部分客户信贷人员由于受到不当利益驱使和利诱，就会突破道德防线，将罪恶之手伸出去收黑钱。进行信贷风险审计，及早发现和处置道德风险，就成为村镇银行防范道德风险的重要保障手段。

在对空间效应进一步分析时，得到以下结论：初始能源强度水平不仅对本地区能源强度的收敛影响显著，且对其他邻近地区影响也显著，说明某地区的能源强度会受到邻近地区的正向影响。人均GDP只对本地区能源强度收敛影响显著，值得关注的是外商直接投资 （FDI），虽然直接效应不显著，但是空间溢出效应显著，说明FDI在区域间存在明显的空间溢出效应。从产业转移角度来看，产业的转入对本地能源强度收敛的影响显著，其空间溢出效应较弱。这是因为企业在进行转移时，会对承接地的生产要素成本进行评估，从而选择最适合的承接地，鉴于各地区资源禀赋的差异，某地区某一产业的转入对本地区能源强度有直接的影响，对邻近其他地区的影响较弱。

(11)

作为农村的一所独立高级中学，学校除了坚持提高教育教学质量之外，还努力发展校园文化建设。校园社团是学生课余时间施展才华、展示风采的大舞台，是提高学生自我管理能力的重要载体，是学校课堂的有益补充和延伸。学校社团在丰富学生学习生活的同时，也推动了学校的文化建设的发展，也成为了校园文化的一道亮丽的风景线。

(12)

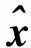
保护区管理处主任朱斌庭介绍，自成立省级保护区后，监利县花220余万元拆除了50万平方米网箱、8000余米“迷魂阵”，拔掉3万余根竹篙；筹资200余万元，在15公里长的核心区江段上下游拦网，为江豚栖息繁育辟出宁静港湾。

(13)

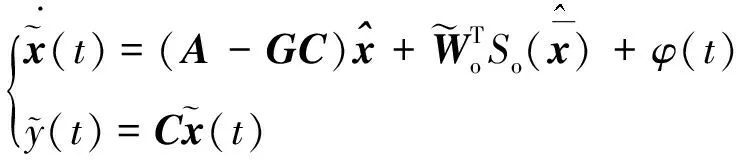
(14)

选取观测器的Lyapunov函数为

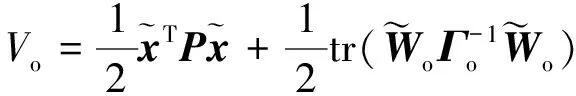
(15)

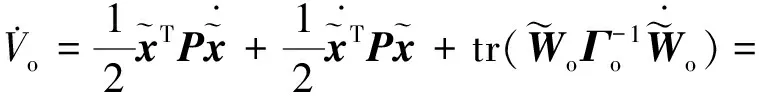
(16)

根据迹的定义可得

(17)

由于

(

)和

(

)中包含系统未知的不确定项,不便于进行反馈控制器设计。为此,本文采用具有较强非线性逼近和学习能力的RBF神经网络对未知非线性函数其进行逼近。同时,将二阶命令滤波器技术引入到反步控制设计中,避免对虚拟控制量进行反复求导。为便于控制器的设计与分析,本文给出如下相关引理和假设。

(18)

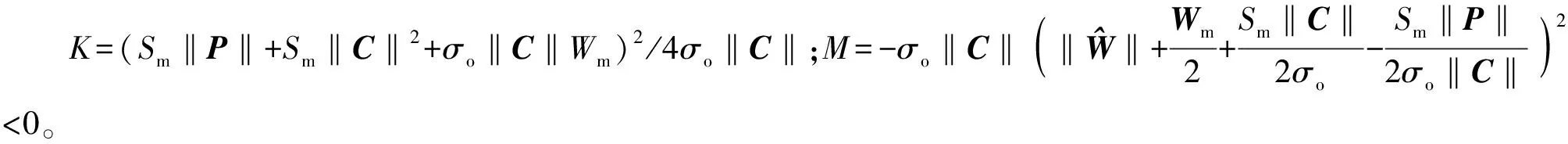
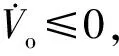
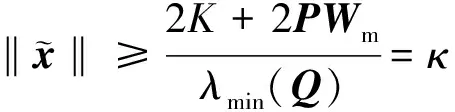
(19)

2.2 命令滤波反步控制器设计

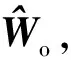
(20)

下面采用命令滤波器反步法来为系统(20)设计输出反馈控制器,控制器设计分4步进行。

(1)控制器仅需机械臂连杆角度的测量信息,且在机械臂模型不精确及受未知干扰时,具有更好的跟踪控制精度和鲁棒性能;

(21)

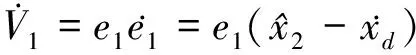
(22)

定义

的虚拟控制输入为

,那么由式(22)可将其设计为

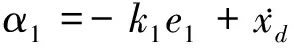
(23)

式中:

>0为待设计的反步控制增益。为避免后续步骤中对

进行多阶求导,使

经过命令滤波器(7)得到

的估计值

及其导数

1

。定义滤波误差

1

以及

的跟踪误差

分别为

(24)

将式(23)(24)代入式(22)得

(25)

:设计虚拟控制

,使

收敛于0。由式(24)可得

(26)

根据引理1,利用RBF神经网络逼近

(

),即

营销业务应用系统是远程费控系统的核心，其主要功能有抄表管理、电费收缴管理、用户关系管理以及能效管理等多种业务，能够有效改善电力营销服务水平，提升电力营销的业务能力，对供电企业营销管理具有重要意义。用电信息采集系统是远程费控系统的终端，主要用于采集安装在用户智能电表提供的电量信息，实现对用户用电数据的实时采集并上传至营销业务应用系统，通过采集的数据分析计量异常状况、电能质量以及预购电等业务，极大地拓展了电力营销的业务，为建设大电力营销体系提供了有力支撑。

(27)

(28)

定义

的虚拟控制输入为

,那么由式(28)可将

设计为

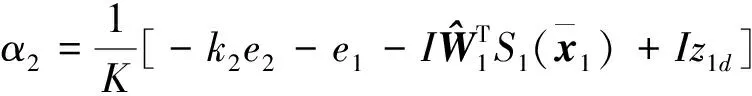
(29)

式中:

>0为待设计的反步控制增益。将

经过命令滤波器(7),得到

的估计值

及其导数

2

。定义滤波误差

2

以及的

跟踪误差

分别为

(30)

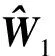
高阻接地故障不同于金属性短路接地，其过渡电阻大，且不同原理的保护反映过渡电阻能力有所不同，因此高阻接地的情况给线路保护提出了挑战。一旦线路保护无法切除接地故障，在主变运行方式以及各级保护配合问题等一系列因素的影响下，将可能发生主变跳闸事故，导致停电范围扩大。因此，需要对高阻接地的特点和保护动作特性进行深入研究，以得到防止此类事故发生的技术措施。

(31)

式中

>0为设计常数。将式(29)～(31)代入式(28)得

(32)

本文研究的控制问题描述为:针对受不确定性影响的柔性关节机械臂式(2),当系统的可测量状态为连杆角度

时,在系统满足假设1和2的条件下,设计基于RBF神经网络的自适应命令滤波反步控制律

,使机械臂

准确快速地跟踪期望轨迹

,实现机械臂的高精度轨迹跟踪。

[7]http://blog.sina.com.cn/s/blog_64e e90340100zjtf.html.

本研究数据采用SPSS 17.0统计软件进行分析，满足正态分布和方差齐性的计量资料采用均数±标准差表示，组间差异比较采用单因素方差分析，两两比较采用LSD法；不满足正态分布的计量资料采用中位数(1/4位数，3/4位数)表示，组间差异比较采用秩和检验。计数资料采用例数(%)表示，组间差异比较采用卡方检验。以P<0.05设定差异具有统计学意义。

(33)

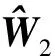
5)消除鸡蛋边界。对鸡蛋轮廓二值图像(图3(c))进行3次腐蚀，将腐蚀后的图像与初步蛋黄提取图像(图4(e))求“与”操纵，最终得到较为完整的蛋黄轮廓特征，如图4(f)所示。

总之，语文生活化，生活语文化。无论哪种方式读写结合，无不彰显《普通高中语文新课标》“语文学科素养是学生在积极的语言实践活动中积累与构建，并在真实的语言运用情境中表现出来的语言能力及其品质，是学生在语文学习中获得的语言知识与语言能力，思维方法与思维品质，情感、态度与价值观的综合体现”这一理念，因为读写结合是语文科本质性的行为表现，语文核心素养的研究也需要以促进学生发展为基础、以语文科塑造人的独立品格与所需能力为基础实现学生终身教育，让我们一起努力践行让生活生命作文与语文核心素养齐飞吧！

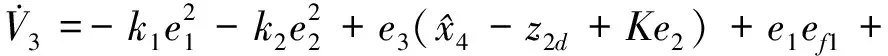
(34)

定义

的虚拟控制输入为

,那么由式(34)可将其设计为

=-

-

+

2

(35)

式中:

>0为待设计的反步控制增益。将

经过命令滤波器(7),得到

的估计值

及其导数

3

。定义滤波误差

3

以及

的跟踪误差

分别为

(36)

将式(35)(36)代入式(34)得

+

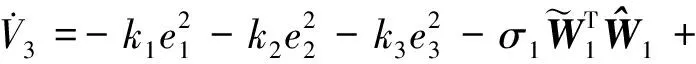
1

+

2

+

3

+

(37)

:设计真实控制输入

,使

收敛于0。由式(36)得

(38)

根据引理1,利用RBF神经网络逼近

(

),即

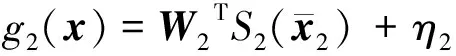
(39)

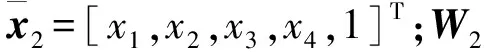
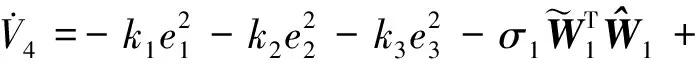
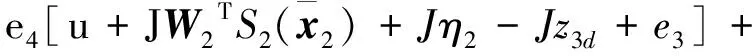
(40)

根据式(40)设计系统真实控制输入

为

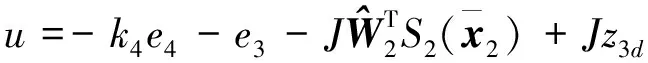
(41)

传统的泡菜制作方式都是采用自然发酵法，发酵周期较长，产品质量不稳定，亚硝酸盐含量也较高[5]。亚硝酸盐的生成和积累极大地影响了泡菜的食用安全性，因为亚硝酸盐在酸性条件下能与胺类及氨基酸等含氮化合物反应，生成具有致癌作用的亚硝胺和亚硝酰胺[6，7]。亚硝酸盐的生成主要在泡菜发酵初期，随着发酵时间的延长，亚硝酸盐的含量也会逐渐降低。但是工业化生产为了提高生产效率，往往缩短发酵周期，亚硝酸盐可能仍维持在较高的浓度。因此，筛选降解亚硝酸盐能力强且生长速率快的乳酸菌菌株对泡菜的生产和推广应用十分重要。

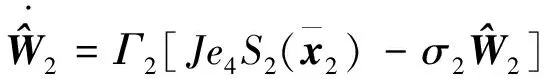
(42)

其中

>0为设计常数。将式(41)(42)代入式(40)得

(43)

综合上述设计步骤,本文设计的命令滤波反步输出反馈控制器结构为

卢春泉的投资理念一直很明确，“就是顺应国家战略，重点投新能源、新材料产业。有些外界炒得很火的概念，像比特币什么的，我们看都不看。”

(44)

式中

(

=1,2,3)为命令滤波器式(7)的输出。

3 控制系统稳定性分析

本节给出柔性关节机械臂在所提控制方法下的控制系统稳定性证明,说明系统跟踪误差信号的一致有界性。

对于柔性关节机械臂式(2),设计自适应命令滤波反步控制器式(44),当机械臂存在模型摄动及外界干扰等未知不确定性时,能够保证跟踪误差控制系统一致最终有界,且误差信号收敛至零附近的任意小邻域内。

选取整个系统的Lyapunov函数为

=

,那么由式(43)得

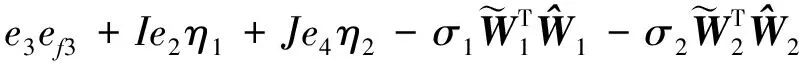
(45)

由于

(46)

结合式(46)整理式(45)可得

(47)

式中:

=min{(2

-1),(2

-

-

),(2

-1),

(2

-

),

,

}

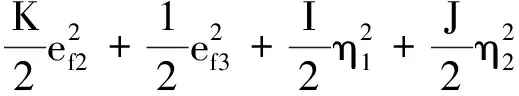
(48)

根据引理3,不等式(47)的解为

(49)

当

→∞,

(

)收敛至上界

。由引理2知滤波误差

(

=1,2,3)有界,已知

(

=1,2)有界,因此控制系统所有的误差信号均可保证一致最终有界。根据假设1和假设2,系统输出信号和所有状态变量均保证一致有界。另外,通过选取适当的控制参数,如增大

(

=1,…,4)和

(

=1,2),可使收敛邻域任意小。

4 仿真结果与分析

在MATLAB/Simulink环境下对上述所提控制方法进行仿真验证。根据文献[19],单关节柔性机械臂的物理参数选取为

=5 N·m,

=1 kg·m

,

=1 kg·m

,

=40 N·m/rad。参考轨迹选取为

=0.5(sin

+sin0.5

)。机械臂的初始值设置为

(0)=[0.5,0,0,0]

,滤波器的参数设置为

=0.8,

=500。自适应神经网络观测器(12)的系统矩阵

=[0,1,0,0;0,0,

,0;0,0,0,1;0,0,0,0],输入矩阵

=[0,0,0,1

]

,输出矩阵

=[1,0,0,0],增益矩阵设置为

=[10,20,0,40]

。式(13)(31)和(42)中的神经网络参数设置为:

=diag(0.05),

=800,

=30,

=3,

=

=50,

o

=[-2,2],

1

=

2

=10[-3,3],

=

=0.002,

=0.005。命令滤波反步控制器式(44)的增益参数设置为:

=5,

=60,

=30,

=5。

下面分两种情形对仿真结果进行分析。

情形1:柔性关节机械臂的模型精确已知,且不受外界干扰影响。

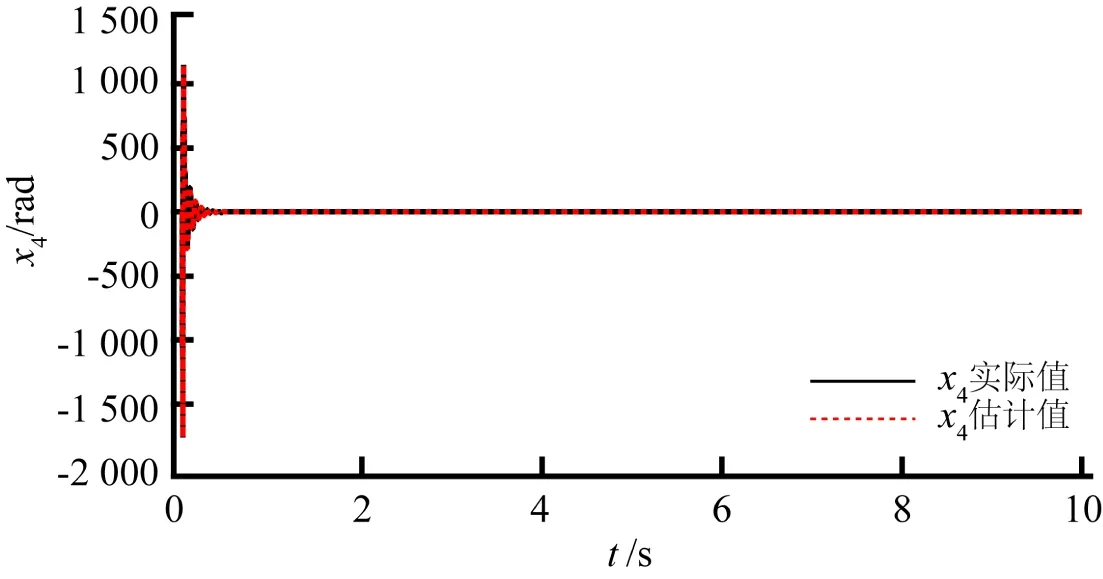
图4(a)～4(c)为本文设计的自适应观测器分别对机械臂状态变量

、

和

的观测结果。图5(a)～5(b)分别为RBF神经网络对未知函数

(

)和

(

)的逼近效果。从图中可以看到,观测器能够快速地观测出系统状态,神经网络也都能准确地逼近出未知函数,达到了较好的观测和逼近效果,从而验证了自适应观测器和神经网络的有效性。

为了更好地体现所提方法的有效性和优越性,选取文献[19]和[27]的控制方法进行对比。仿真中,为保证对比的公平性,3种方法的系统参数与控制器参数均保持一致。

图6和图7为3种控制方法在情形1条件下的仿真结果,其中,图6为关节角位置跟踪曲线,图7为跟踪误差变化曲线。从图6中可以看出,3种控制方法均可以跟踪上参考轨迹,但是相比于文献[27]方法,本文方法具有更快的跟踪速度,与文献[19]方法非常接近。另外由图7可见,本文方法的跟踪误差最终收敛到了零的小邻域内,但是稳态误差要略大于其他两种方法,这是因为文献[19]和[27]均是基于理想模型设计的。当机械臂的模型精确已知且不受干扰影响时,文献[27]的跟踪误差能够实现渐近稳定,文献[19]的跟踪误差能够收敛至零的小邻域内,该邻域的范围取决于命令滤波器的滤波精度。本文方法为了克服对理想模型和全状态反馈的依赖性,同时引入了命令滤波器、自适应神经网络和状态观测器,使跟踪误差与滤波精度、神经网络逼近精度和观测器观测误差均有关,从而导致稳态误差要略大。

情形2:柔性关节机械臂的模型参数存在摄动,且受未知外界干扰影响。

为进一步说明本文方法的优越性,考虑柔性关节机械臂受如下不确定性的影响

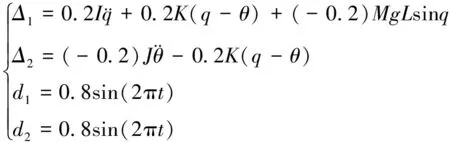
(50)

3种控制方法在情形2下的仿真效果如图8和图9所示。

图8和图9分别为连杆角位置跟踪和跟踪误差效果对比图。从对比结果中可以看出,文献[19]和[27]的方法受不确定性的影响较大,特别是文献[27],跟踪效果产生了明显的波动和偏差。由图9可知,文献[27]方法的跟踪误差幅值约为8.3×10

rad,文献[19]方法的跟踪误差幅值约为2.8×10

rad,而本文所提方法的跟踪误差约为1.8×10

rad,因此相比于文献[19]和文献[27],所提方法的跟踪精度分别提高了35%和78%,保证了机械臂的高精度轨迹跟踪控制。

综上,通过两组仿真实例可以看出,不论是柔性关节机械臂是否存在不确定性,本文提出的控制方法均获得了较满意的控制效果。特别是当机械臂受不确定性影响时,相较于其他两种方法,本文方法有较快的跟踪速度和较小的稳态误差,同时保证了良好的瞬态性能和稳态精度。

5 结 论

本文为柔性关节机械臂提出了一种基于自适应神经网络观测器的命令滤波输出反馈跟踪控制方法,实现了机械臂高精度的轨迹跟踪控制。该方法通过RBF神经网络自适应律设计使得控制器不依赖于机械臂精确的数学模型;通过自适应状态观测器设计使得控制器只需测量连杆的角度状态信息。此外,通过引入二阶命令滤波器避免了反步设计中需要逐步计算中间虚拟控制量导数的不足。严格的理论证明保证了闭环系统中的所有误差信号的一致最终有界性。对比仿真结果也表明,所提方法在系统同时存在不确定性和状态信息不可测时,具有更高的跟踪精度和更好的鲁棒性能。

值得说明的是,本文通过引入二阶命令滤波器避免了“计算爆炸”的问题,但在一定程度上也增加了滤波误差。对于该误差,论文通过增大滤波器带宽的方式使误差变得足够小,从而保证了跟踪精度。未来的工作将考虑引入误差补偿机制对滤波误差进行补偿,以进一步减小滤波器带宽和提高跟踪精度。

:

[1] CHEN Ti, SHAN Jinjun. Distributed control of multiple flexible manipulators with unknown disturbances and dead-zone input [J]. IEEE Transactions on Industrial Electronics, 2020, 67(11): 9937-9947.

[2] MA Hui, ZHOU Qi, LI Hongyi, et al. Adaptive prescribed performance control of a flexible-joint robotic manipulator with dynamic uncertainties [J/OL]. IEEE transactions on cybernetics, 2021 [2021-10-20]. DOI: 10.1109/TCYB. 2021.3091531.

[3] ABDUL-ADHEEM W R, IBRAHEEM I K, HUMAIDI A J, et al. Model-free active input-output feedback linearization of a single-link flexible joint manipulator: an improved active disturbance rejection control approach [J]. Measurement and Control, 2021, 54(5/6): 856-871.

[4] KORAYEM M H, NEKOO S R, KAZEMI S. Finite-time feedback linearization (FTFL) controller considering optimal gains on mobile mechanical manipulators [J]. Journal of Intelligent & Robotic Systems, 2019, 94(3): 727-744.

[5] 杨春雨, 许一鸣, 代伟, 等. 柔性机械臂的双时间尺度组合控制 [J]. 控制理论与应用, 2019, 36(4): 659-665.

YANG Chunyu, XU Yiming, DAI Wei, et al. Two-time-scale composite control of flexible manipulators [J]. Control Theory & Applications, 2019, 36(4): 659-665.

[6] 孙小通, 马磊, 李梦雪, 等. 基于自适应滑模-最优控制的柔性机械臂双时标组合控制 [J]. 噪声与振动控制, 2020, 40(5): 22-26, 45.

SUN Xiaotong, MA Lei, LI Mengxue, et al. Dual time-scale combined control of flexible manipulators based on adaptive sliding-mode and optimal control [J]. Noise and Vibration Control, 2020, 40(5): 22-26, 45.

[7] 党进, 倪风雷, 刘业超, 等. 一种前馈补偿和模糊滑模相结合的柔性机械臂控制 [J]. 西安交通大学学报, 2011, 45(3): 75-80.

DANG Jin, NI Fenglei, LIU Yechao, et al. Control strategy for flexible manipulator based on feedforward compensation and fuzzy-sliding mode control [J]. Journal of Xi’an Jiaotong University, 2011, 45(3): 75-80.

[8] MAHMOODABADI M J, NEJADKOURKI N. Trajectory tracking of a flexible robot manipulator by a new optimized fuzzy adaptive sliding mode-based feedback linearization controller [J]. Journal of Robotics, 2020, 2020: 8813217.

[9] 史超. 柔性机械臂的多时间尺度滑模控制 [J]. 控制工程, 2020, 27(9): 1560-1565.

SHI Chao. Sliding-mode control of flexible manipulators in multiple time scales [J]. Control Engineering of China, 2020, 27(9): 1560-1565.

[10]马驰骋, 罗亚军, 张希农, 等. 基于模糊PID控制器的变质量-柔性梁结构振动主动控制 [J]. 振动与冲击, 2018, 37(23): 197-203, 240.

MA Chicheng, LUO Yajun, ZHANG Xinong, et al. Vibration active control of a flexible beam with time-varying mass based on fuzzy PID controller [J]. Journal of Vibration and Shock, 2018, 37(23): 197-203, 240.

[11]ABD LATIP S F, RASHID HUSAIN A, MOHAMED Z, et al. Adaptive PID actuator fault tolerant control of single-link flexible manipulator [J]. Transactions of the Institute of Measurement and Control, 2019, 41(4): 1019-1031.

[12]WANG Lijun, SHI Qiuyue, LIU Jinkun, et al. Backstepping control of flexible joint manipulator based on hyperbolic tangent function with control input and rate constraints [J]. Asian Journal of Control, 2020, 22(3): 1268-1279.

[13]SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems [J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899.

[14]顾义坤, 倪风雷, 刘宏. 基于RENN的柔性关节机械臂自适应动态面控制 [J]. 控制与决策, 2011, 26(12): 1783-1790.

GU Yikun, NI Fenglei, LIU Hong. Flexible-joint manipulator adaptive control based on recurrent Elman neural networks and dynamic surface approach [J]. Control and Decision, 2011, 26(12): 1783-1790.

[15]LING Song, WANG Huanqing, LIU P X. Adaptive fuzzy dynamic surface control of flexible-joint robot systems with input saturation [J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(1): 97-107.

[16]DONG Wenjie, FARRELL J A, POLYCARPOU M M, et al. Command filtered adaptive backstepping [J]. IEEE Transactions on Control Systems Technology, 2012, 20(3): 566-580.

[17]FARRELL J A, POLYCARPOU M, SHARMA M, et al. Command filtered backstepping [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395.

[18]LING Song, WANG Huanqing, LIU P X. Adaptive fuzzy tracking control of Flexible-Joint robots based on command filtering [J]. IEEE Transactions on Industrial Electronics, 2020, 67(5): 4046-4055.

[19]李鹏飞, 张银河, 张蕾, 等. 考虑误差补偿的柔性关节机械臂命令滤波反步控制 [J]. 控制理论与应用, 2020, 37(8): 1693-1700.

LI Pengfei, ZHANG Yinhe, ZHANG Lei, et al. Command-filtered backstepping control with error compensation for flexible joint manipulator [J]. Control Theory & Applications, 2020, 37(8): 1693-1700.

[20]林孟豪, 张蕾, 李鹏飞, 等. 考虑输出约束的机械臂命令滤波反步控制 [J]. 西安交通大学学报, 2021, 55(12): 70-78.

LIN Menghao, ZHANG Lei, LI Pengfei, et al. A backstepping control strategy of command filtering for two-link flexible joint manipulator [J]. Journal of Xi’an Jiaotong University, 2021, 55(12): 70-78.

[21]LIU Xin, YANG Chenguang, CHEN Zhiguang, et al. Neuro-adaptive observer based control of flexible joint robot [J]. Neurocomputing, 2018, 275: 73-82.

[22]YAN Ze, LAI Xuzhi, MENG Qingxin, et al. A novel robust control method for motion control of uncertain single-link flexible-joint manipulator [J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 1671-1678.

[23]TALOLE S E, KOLHE J P, PHADKE S B. Extended-state-observer-based control of flexible-joint system with experimental validation [J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1411-1419.

[24]RSETAM K, CAO Zhenwei, MAN Zhihong. Cascaded-extended-state-observer-based sliding-mode control for underactuated flexible joint robot [J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10822-10832.

[25]侯捷, 陈谋, 刘楠. 基于径向基函数神经网络与扩张状态观测器的无人直升机控制 [J]. 控制理论与应用, 2021, 38(9): 1361-1371.

HOU Jie, CHEN Mou, LIU Nan. Unmanned helicopter control based on radial basis function neural network and extended state observer [J]. Control Theory & Applications, 2021, 38(9): 1361-1371.

[26]李彬, 徐怡杭, 罗杰. 采用残差神经网络的无人机遥控信号识别监测算法 [J]. 西安交通大学学报, 2021, 55(12): 146-154.

LI Bin, XU Yihang, LUO Jie. A recognition and monitoring algorithm for drone remote control signals using residual neural network [J]. Journal of Xi’an Jiaotong University, 2021, 55(12): 146-154.

[27]HUANG A C, CHEN Y C. Adaptive sliding control for single-link flexible-joint robot with mismatched uncertainties [J]. IEEE Transactions on Control Systems Technology, 2004, 12(5): 770-775.

[28]CHIEN M C, HUANG A C. Adaptive control for flexible-joint electrically driven robot with time-varying uncertainties [J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 1032-1038.

[29]HARTMAN E J, KEELER J D, KOWALSKI J M. Layered neural networks with Gaussian hidden units as universal approximations [J]. Neural Computation, 1990, 2(2): 210-215.

[30]PARK J, SANDBERG I W. Universal approximation using radial-basis-function networks [J]. Neural Computation, 1991, 3(2): 246-257.

[31]NARENDRA K S, ANNASWAMY A M. Robust adaptive control [M]. Boston, USA: Springer, 1986: 3-31.