游荡型河道河势突变调整的内涵与研究方法

张向萍，江恩慧，李军华，王远见，万 强

（1.黄河水利科学研究院，河南 郑州 450003；2.河海大学 水利水电学院，江苏 南京 210098；3.水利部黄河下游河道与河口治理重点实验室，河南 郑州 450003）

1 研究游荡型河道河势突变调整的现实意义

游荡型河道是天然河流中最难治理的河型之一。游荡型河道具有独特的地貌形态和极其复杂的演变规律，如断面宽浅、洲滩密布、汊道交织、水流散乱、主槽迁徙不定等。一般情况下游荡型河道河势以渐变的形式进行调整，而在大洪水期或者边界约束变化较大的地方，会出现较大幅度的突变。

随着经济社会的发展，为了满足不断增长的生存和发展需求，人类开始大规模修建大坝，大大改变了进入河流的水沙过程。同时，在河流两岸修建了大量的河道整治工程，原有天然（或约束相对较弱）的河道边界逐步演变为由河道整治工程与天然河岸共同组成的软硬边界，天然河道演变为强人类干扰下的有限控制边界河道。有限控制边界的游荡型河道河势在小水时期有节点工程约束的地方也会表现出突变。

游荡型河道河势突变调整给河流防洪、供水安全及河流治理带来了很多不利的影响。如黄河下游洪峰过后落水期局部河段河势突变，多产生畸形河湾，导致“横河、斜河”等不利河势出现，严重影响防洪工程及滩区居民安全，如图1（a）所示。2013年黄河下游花园口河段河道发生剧烈调整，主流从原来郑州白庙水厂花园口取水点位置向北偏移了2 km，致使2013年11月底至2014年1月取水泵站无法正常引水，郑州市半城只能降压供水，至今仍采用清淤开挖引河的方法解决引水问题，如图1（b）所示。

图1 河道突变调整对防洪、供水等影响

此外，在防洪方面，可以利用改变水沙条件或者局部边界条件助推局部河势发生突变调整，加速将不归顺的河势向有利方向转化，提高应对洪水灾害的韧性，减轻灾害风险。

本文以游荡型河道河势突变为研究对象，探讨河势突变的内涵、研究方法和临界条件，为下一步开展河势突变研究厘清方向，为预防河势突变产生的危害或利用河势突变增强河势稳定性提供帮助。

2 游荡型河道河势突变调整的内涵

河势突变是指游荡型河道局部河段或整体河段河势在很短的时间内发生了大幅度的调整。河势突变调整是相对于河势渐变调整而言的，河势渐变是指河势缓慢连续相对较小的变化过程，河势渐变调整中河势的趋势或状态未发生根本的变化，主流或水边的位置处于动态微调当中。河势突变是河势由一种动态渐变状态向另外一种动态渐变状态调整的突变过程。游荡型河道河势变化通常表现出渐变特征，而在水沙发生剧烈变化或者边界约束作用发生较强变化的地方，如河道边界受到人为活动的强烈干扰时，河势调整可能表现出突变特征。

在工程应用上，河势突变不只会给河流防洪、供水安全、河道工程管理等带来重大的挑战，反过来，如果在某些情况下对河势突变适当加以利用，可有效提高河道整治工程的控导能力，增强河势稳定性。

以黄河下游为例，为了稳定河势，对黄河下游游荡型河道目前采用微弯型整治方案进行工程布局，通过河道整治工程的控流、导流功能，使水流能够按规划流路演进，如图2所示。在此将工程本身的有效送流距离用X表示，已有研究表明其主要与流量、工程靠流长度、工程弯曲半径、送流角度等因素有关；河道整治工程末道坝的坝头切线至下一处工程的距离用e表示。若X与e值接近，说明工程配套较好，能有效地控制两河湾工程之间的河势；若X小于e过多，说明工程送流能力较弱（如小水期主流下败），难以送流至下一工程，导致下一工程不靠流或靠流概率大大减小，不能按规划流路控制河势［1］。要消除这一影响，必须调整工程布设方案，使其突破现有河道整治工程有效送流能力的阈值。

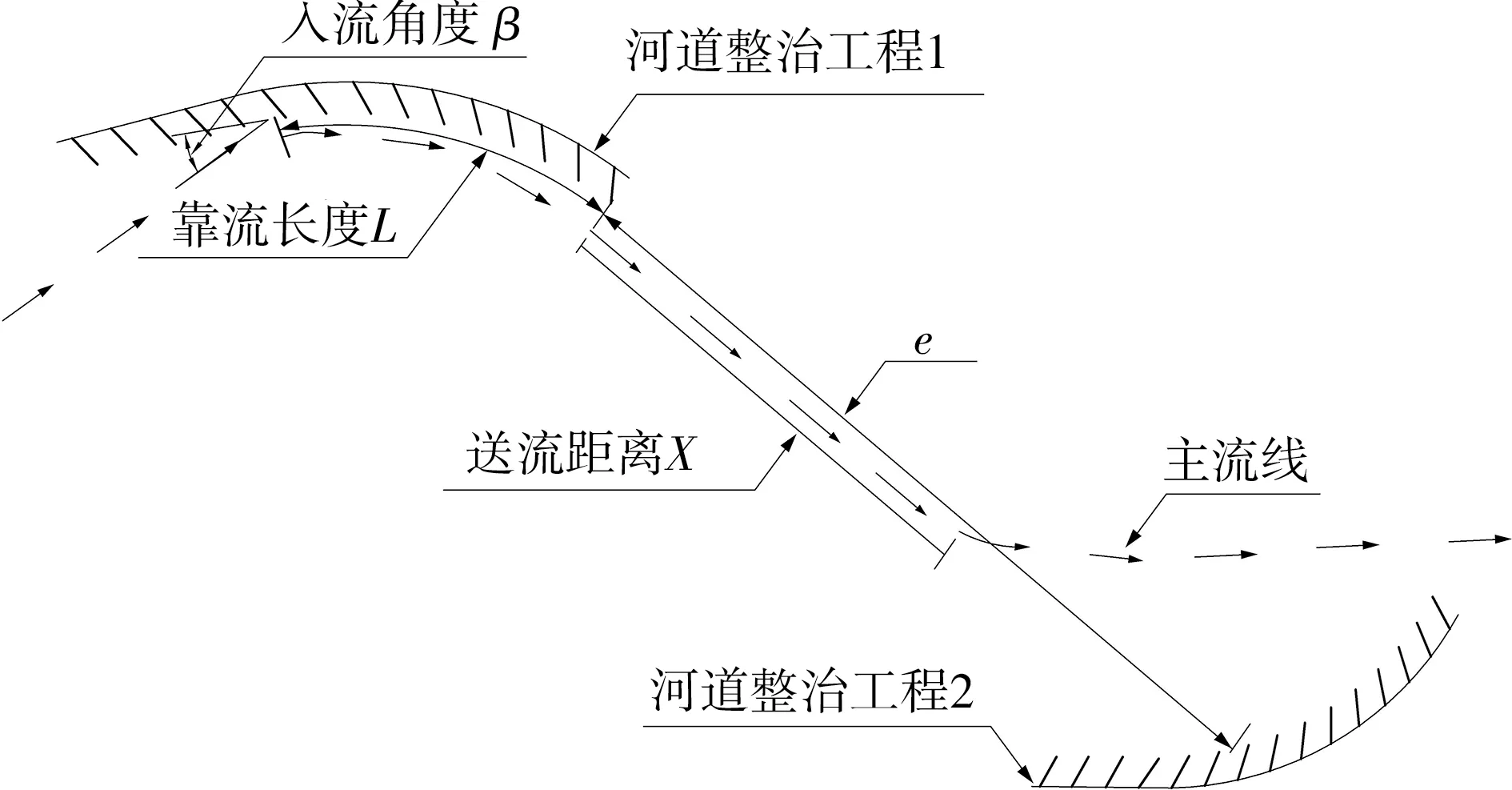
图2 河道整治工程送流距离示意

例如20世纪90年代初，修建黄河下游马渡下延工程的目的之一就是改变原有河势，将主流稳定送至对岸武庄控导工程，以保证对主流的强有力控导，并稳定送流至对岸赵口控导工程，保障供水安全。江恩惠等［1］通过开展多组次的物理模型试验后，提出了减小马渡下延工程送流半径的建议，但是并未引起工程界的重视，导致在工程实践中多年未能奏效。2000年开始的新一轮黄河下游游荡型河道整治工程建设中，适度减小了原有工程河弯半径，有效提高了工程的送流能力，引发河势突变调整，将主流顺利送至武庄工程，且近20 a来武庄工程始终稳定靠流，如图3所示。

图3 马渡—武庄工程河段河势突变

河势突变的内涵是由水沙剧烈变化或者具有约束作用的边界发生较大变化而引起的游荡型河道河势由一种动态渐变状态向另外一种动态渐变状态调整的突变过程。在不同的时空尺度上，河势突变的表现形式不同。从宏观尺度上，河流改道和河型转化是冲积河流系统河势突变的两个典型现象。在较小空间尺度上，如针对某一河段，裁弯取直、畸形河湾形成、横河斜河同样是河势突变的结果。

3 游荡型河道河势突变调整的研究方法

在水沙和边界条件的控制下，河流在平面、纵横断面上的调整是河床演变学研究的主要内容。单就河势而言，在人类活动日益加剧的今天，水沙条件、河床自然边界和工程边界条件在时空上的不同组合构成了千差万别的外部影响条件，导致了复杂多变的河势演变过程和形式［1］。这其中，水沙条件是影响河势演变幅度和剧烈程度的根本因素，河床条件提供了河势演变的发展空间，影响河势的变化幅度和剧烈程度。两者相互作用，使得河势朝着与来水来沙相适应的平衡状态发展。

早期河床演变学的研究多关注在自然状态下水沙与河床形态之间的定量关系，如河相关系、水力几何形态关系等。随着流域水沙条件的变化和人类活动对河床边界的大规模改造，强人工干预下河流的河床演变过程逐渐成为新的研究热点。这种演变调整过程遵循由量变到质变、由渐变到突变的变化规律。根据变化的形式，将游荡型河道的河势演变过程分为河势渐变调整和河势突变调整。目前，对游荡型河道河势渐变过程及规律的研究较多，而对于突变过程，常用的研究方法主要有理论研究、数值模拟和物理模型试验。

3.1 游荡型河道河势突变理论研究

现有河床演变理论的研究建立在基于时空连续性假设的微积分学和牛顿力学理论体系之上。一般情况下，河床演变是一个渐变过程。这个渐变过程可采用基于时空连续性假设的微积分方程来描述。流体在可动边界中的运动满足非线性NS方程，冲积河流的河床是由松散的泥沙组成的，因此其河床演变也存在非线性过程。当水流条件发生变化或者河床边界受到扰动时，河流随之发生自调整过程。这种自调整或者是向原有的平衡态恢复（稳定平衡），或者是向新的平衡态调整（不稳定平衡）。对这一调整速率的研究是建立现有河道渐变理论模型的关键。

需要指出的是，在自然或人工扰动使河道形态在旧平衡态附近波动时，调整速率的线性假设是近似成立的；而在强不平衡水沙条件下，河床发生剧烈的冲淤演变，此时河床演变的非线性规律更加突出。吴保生等［2-6］将非线性特征应用于河道调整进程，指出冲积性河流的河床在由不平衡态向平衡态演进的过程中，调整变化速度随时间呈指数衰减的趋势。这些研究从系统动力学的层面揭示了河流系统的渐变规律，但在河势突变上仍缺乏理论认识。

游荡型河道河势演变具有由渐变到突变的特性，当水沙动力或边界条件突破一定的临界时，就会引发河势的突变现象。由于对河势突变现象力学机理和理论研究的欠缺，因此目前对河势突变调整的研究，多针对某种特定的条件和某种具体的突变现象，重点研究突变发生的临界条件。

宏观尺度上，河型转化和河流改道是游荡型河道河势突变的两种典型现象。基于对实测资料的分析，多位学者基于地貌临界假说、水流能耗率极限假说、稳定性理论、随机理论、突变理论等就河型转化提出了相应的河势稳定性指标与不同河型转化的临界参数［7-17］。肖毅等［18］利用突变理论中的尖点突变模式分析并提出了河型转化的临界判别条件。赵丽娜等［19］基于非平衡态热力学理论的超熵构造出超能耗率，推导出河型稳定判别式和河型转化的临界条件。

在河道迁移改道方面，Slingerland等［20］应用一维模型研究了弯曲型河流发生改道的必要条件，指出对于从细沙到中等粒径的泥沙，当决口坡度大于其所在的主河道坡度8倍时，决口就会吸引整个主流流量。王万战等［21］分析了现代黄河口河道的演变规律，揭示了黄河口流路由单股河道逐渐转为出汊的过程，认为在多重因素影响下，河口河道纵剖面逐渐形成台阶状，滩地横比降发展成为倒比降，河口河道中段由顺直型河道逐渐转为弯曲型河道，下段为相对顺直、游荡型河道，当中段比降减小到一定程度时，开始出现漫滩、卡冰、出汊等。Wang等［22］利用历史文献资料结合改道速度、流路方向、分流点位置、纵比降、弯曲度等分析了有文献记载以来黄河下游数次改道的地理变化特征，结果显示河道行河时间与河床纵比降呈正相关，与弯曲度呈负相关。在王兆印等［23］的研究中也提到黄河三角洲河流的延伸减小了其纵比降和河道的过流、输沙能力，导致河流改道，新的河道长度为先前河道长度的1／3～1／2，而比降是先前的2～3倍。

在较小空间尺度上，如针对某一河段，横河斜河、畸形河湾形成同样是河势突变的表现形式。

横河、斜河被定义为游荡型河段水流在无工程控导下，全河或其中主股急转弯，其流向与宏观流向或堤、岸相垂直或近于垂直，并稳定一定时段的河势状态。横河、斜河为河势突变的典型代表，方宗岱［24］探讨分析了浅水河流河床演变的斜河现象；李希宁等［25］分析了山东黄河河道发生横河、斜河的原因及其防御生险的措施；王恺忱等［26］基于黄河下游河势演变资料总结了横河、斜河的多发部位、原因及防治措施。吴腾等［27］初步探讨了黄河下游斜河现象的形成原因和机理；胡一三［28］总结了黄河下游横河的多发河段和时段，并指出了横河的形成原因及其与河道整治的关系。

畸形河湾是河势突变的另一种重要表现形式。胡一三等［29］对黄河下游高村至陶城铺过渡型河道的畸形河湾裁弯现象进行了详细分析，认为河道边界中出露的耐冲黏土层（胶泥嘴）在畸形河湾的形成中起着重要的作用，河道整治是控制畸形河湾的重要措施。20世纪80年代以后，黄河下游游荡型河段因长期小水，也出现了大量畸形河湾。许炯心等［30］对黄河下游畸形河湾的形成、演变过程及机理进行了研究，认为游荡段畸形河湾的形成机理与过渡段相同，但促使游荡段畸形河湾形成的节点常常是人工节点（河道整治工程），是水沙过程改变后与人为工程边界条件不适应而出现的一种剧烈河势调整，这一认识与实际情况有不符之处。江恩惠等［1］对黄河下游的畸形河湾进行系统分析后指出：黄河下游河道的淤积物成层分布及陡涨陡落的洪峰过后长期的中小水作用，使水流坐弯淘刷岸滩并持续发展，是畸形河湾形成的主要原因。胡一三［31］利用黄河下游的河势演变资料，比较全面地描述畸形河湾的发展过程及不利影响。万强等［32］分析了黄河下游在长期小水作用下产生的畸形河势，并提出了改善畸形河势的调度方式。

开展河道自调整规律研究已有百余年的历史，学者们大都基于微积分学和牛顿力学理论体系从系统动力学层面研究河流系统的渐变规律。随着非线性科学的发展，河床演变的非线性现象受到关注。现实中游荡型河道河势突变现象是河床演变的重要组成部分，关于这些现象在理论上仍缺乏认识，关于它们演化的机理研究也十分欠缺，目前这一领域迫切需要引入新的理论和方法，为解决游荡型河道河势突变相关工程问题提供科学支撑。

3.2 游荡型河道河势突变数值模型研究

现有河床演变学研究多采用定量的力学分析方法和定性的逻辑推理方法，一般是根据观测资料寻求定性或定量的经验关系、数学模型模拟、实体模型模拟等。目前关于游荡型河道河势突变的研究方法和手段也多是这几种，倾向于针对某一个问题或现象采用两种或两种以上的方法进行研究，随后用其他手段进行验证。

在利用数学模型开展河势突变研究方面，解析模型、元胞自动机模型以及水沙动力学模型等被尝试用于河势模拟。Thorne等［33］基于解析模型模拟了高弯曲度的河道演变过程和河道裁弯现象。Asahi等［34］完整模拟了河道由顺直到弯曲再发生裁弯的过程。元胞自动机模型可模拟地质时间尺度的河道演变，Douglas等［35］利用元胞自动机模型模拟冲积性河流的改道过程，认为一个单一的超高阈值可以引发多种不同大小和类型改道。元胞自动机模型基于随机游移，假定较多，且参数物理意义不明确，所以在模拟河势突变上不甚理想。

水沙动力学模型可以分为一维、二维、三维的水流和泥沙数学模型。一维模型利用公式（方程）直接求解，无法模拟水流的横向和垂向变化，因此在模拟河势突变方面存在严重不足。二维模型克服了一维模型的不足，能够反映河道河势的平面变化，且计算效率较高，因此得到了广泛应用。河床的横向变形、滩岸崩塌被认为是造成河势突变的原因之一，Huang等［36］认为河床横向变形是泥沙的侧向冲刷和河岸淘蚀综合作用的结果，引进土力学中有关河岸力学平衡的基本关系，提出了黄河下游河床横向变形的数值模拟方法；夏军强等［37］提出了基于河宽调整力学模拟技术的平面二维模型，模拟计算河床纵向冲淤过程和三类土质河岸的坍塌与淤长过程，反演游荡型河段在复杂地形条件下河床演变的物理过程；钟德钰等［38］在游荡型河流平面二维水沙数学模型中引入适合游荡型河流的塌岸模式，解决了河岸变形模拟和河道整治工程导致网格再生、床沙级配变化模拟等关键性技术问题，开发了模拟游荡型河流河床演变及可反映河道整治工程作用的平面二维水沙数学模型，并用于黄河下游游荡型河道河势变化的模拟计算；周刚等［39-40］采用考虑弯道二次流影响与边岸崩塌过程的平面二维河流数学模型模拟得到了初始比降、流量、入口含沙量增大和河岸抗冲性减弱时河流从弯道向分汊、游荡河型转化的过程。随着模拟技术的进步和计算效率的提高，更为复杂的三维模型逐渐被发展起来，它能够比较准确地模拟弯道泥沙输移的细部结构，如假冬冬等［41］以荆江监利河段为例构建了考虑边岸、洲滩崩塌的分汊型河道演变三维数值模型，宋晓龙等［42］分析提出既能反映非线性又能反映突变性特征的分数-泊松扩散模型。随着科技手段的进步，3S技术、无人机、大数据、人工智能等新技术和新手段将被用于河床演变研究，针对河势变化研

究的数学模型将得到不断完善和发展。

3.3 游荡型河道河势突变物理模型研究

实体模型试验一直是开展河床演变研究的主要手段，在研究河势突变方面，倪晋仁［13］概化试验表明，由初始顺直开始发展的河流，无一例外地或迟或早经过流路弯曲形成弯曲型河流，如果边滩稳定则保持弯曲型河流，否则切滩形成游荡型河流。Bryant等［43］在一个小型水槽（1.6 m×3.0 m×0.3 m）中模拟冲积扇上河道的演化，发现河流改道频率和沉积速率成正比。张红武等［15］以黄河下游游荡型河段为模拟对象开展了自然河工模型试验，结果表明上游来沙量的大小与河道稳定性有极为密切的关系。江恩慧等［44］曾制作了一系列模型小河，通过试验研究认为，只要水流保持相应的强度，任何可动河床边界条件下都可能形成游荡型、分汊型及弯曲型河流。Meredith等［45］利用1 m×1 m×3 m的试验水槽模拟冲积扇和三角洲上河道改道分流过程，并构建了改道周期的公式，提出改道周期等于淤积速率与河道深度的比值。Clarke等［46］通过一个3 m×3 m×0.7 m水槽和高清摄像头来模拟和观察3种不同水沙情景下冲积扇的演化过程以及扇面上河道的迁移。Zhang等［47］模拟得出泥沙供给减小的条件下冲积扇上河道化加快，河流改道循环的时间更长。随着计算机技术的发展，虽然实体模型的一些功能被数学模型所取代，但是在模拟河道的自组织演化、河势突变、复杂行为过程、未知规律等方面仍然具有优势。万强等［32］根据实体模型试验结果系统研究黄河下游游荡型河段4处畸形河湾不同流量条件下河势变化特点及规律，指出目前仅依靠小浪底水库泄放中常洪水的水动力改善畸形河湾并不现实。

4 结论与建议

游荡型河道河势突变调整是河流自组织调整过程中的一类典型现象。它表示游荡型河道河势在相对较短的时间内发生较大幅度的变化，以此来适应流域来水来沙条件和河流边界。

游荡型河道河势突变一般对应着特定的水沙动力和地貌临界条件，如果达到或超过这一临界条件，就会引发河势突变现象。基于现有河床演变理论对河势突变的机理认识尚不清晰，主要表现在以下几个方面：①对游荡型河道河势突变调整的现象和过程多是定性的描述和总结，缺乏定量的认识以及明确的数学表达形式；②河势突变现象比较复杂，目前对河势突变调整的路径和模式也不明确，对引发突变现象背后物理机制认识还不足，因此还不能在理论上描述河势突变；③从工程意义上来说，正是这种理论上的缺失使目前的河道整治工程设计无法定量评估河势突变发生的可能，应用工程手段进行河势控制的效果仍存在较大的不确定性。

对于游荡型河道河势突变调整现象，亟须进一步开展深入和系统的研究。在研究过程中需要着重关注以下问题：①针对不同类型的河势突变，遴选不同的影响因子，构建不同的数学表达式；②厘清游荡型河道河势突变发生的模式、调整路径以及可能的响应方式；③提出适应于不同条件下不同类型河势突变的临界条件，评估游荡型河道发生河势突变的可能，提出防止或引导突变发生的工程措施。

此外，在研究中将数学领域专门用于研究不连续过程的突变理论、系统科学领域其他分析方法以及传统的牛顿力学等研究方法相结合，数学模型与实体模型等研究手段相结合，适时引入3S技术、人工智能、大数据分析等新技术，揭示游荡型河道河势突变调整的机理，为防止或引导河势突变调整提供有效的科学支撑。