SCS-CN模型在小流域产流计算中的应用

2022-05-20张晓涵桑国庆

人民黄河 2022年5期

张晓涵，桑国庆

（济南大学水利与环境学院，山东济南 250022）

山洪是最严重的自然灾害之一，山丘区小流域洪水径流流速快、水量集中、滞时短，极易暴发局部洪灾，且山洪具有很强的冲刷破坏力，会造成极端危害［1］。沂源县是山东省平均海拔最高的县，为典型的山区县，洪涝威胁严重，特别是20世纪90年代以来极端天气事件增多，经常发生集中暴雨，形成较大洪水，曾在1993年、1994年、1998年、2001年、2007年发生过较为严重的山洪灾害。合理预测山丘区小流域洪峰是山洪灾害预报预警重要的基础工作和关键环节，深入研究小流域产流规律则是山洪洪峰计算的重要环节之一，也是一个非常重要的研究课题，现有的许多水文模型存在输入参数多、参数获取和率定比较困难等问题，美国农业部水土保持局于20世纪50年代开发的用于估算地表径流量的径流曲线数（SCS-CN）模型，结构简单、所需参数较少、模拟结果准确度较高，能够客观反映土壤类型、土地利用方式及前期土壤含水量对降雨径流的影响，被广泛应用于地表径流预测。

径流曲线数C N值是SCS-CN模型中反映下垫面对产流过程影响的关键参数，其敏感性非常高。Boughton［2］的研究表明，径流量Q随平均湿润状况下CN值的变化而变化，CN值变化±10%，会导致径流量变化±50%。李鑫川等［3］分析了SCS-CN模型参数的敏感性，各参数的总敏感性排序依次为：CN、b、λ（b为蓄水能力系数，λ为初损率）。刘贤赵等［4］应用SCS模型按照研究区集水区自然分水线划分流域子单元，提出了适合黄土高原典型流域产流计算的CN值表。邓景成等［5］利用模拟降雨资料应用平均值法等5种方法计算C N值，确定了不同流域的最优计算方法，证明了不同土地利用类型下CN值最优计算方法不同。初损率λ是SCS-CN模型的基础参数，是降雨径流过程初损值与最大潜在蓄水量的比值，是影响模型模拟精度的一个重要影响因素［6］。SCS-CN模型标准计算公式中λ采用了一个适用于美国北部地区的标准值0.2，实际应用中λ的取值存在区域性差异，标准值并不能完全适用于其他区域［7］。徐赞等［8］使用反算法、MATLAB结合粒子群算法优化黄土高原地区韭园沟流域初损率，并引入雨强因子修正径流曲线法。张钰娴等［9］在对径流曲线数模型参数λ敏感性分析的基础上，应用实测降雨资料对参数λ与地表坡度关系进行了定量分析。王红艳［10］研究表明当CN值一定时，初损率λ相对敏感性会随着降雨量的增加而减小，尤其是在以农田草地为主的流域，对初损率λ取值最敏感。

笔者以沂源县为研究区，根据土壤类型及土地利用类型确定沂源县24个小流域的径流曲线数CN值，根据小流域实测降雨径流资料以Nash公式中的模型效率系数E、标准均方根误差NRMSE、模型合格率作为判断依据确定适合沂源县的初损率λ，提高了模型径流模拟精度，应用效果良好。

1 研究区域概况

沂源县位于山东省淄博市最南端，处于东经117°48′—118°31′、北纬35°55′—36°23′之间。县域东西长55.6 km，南北宽52.2 km，总面积1 636 km2。沂源县是山东省平均海拔最高的县，平均海拔400 m，海拔最高的鲁山海拔为1 108 m，为山东第四高峰。域内地形复杂，地貌类型较多，主要有中山、低山、丘陵和山前倾斜平地几种，东南沂河谷地海拔仅为180 m，中山、低山和丘陵面积占99.3%。沂源县属暖温带亚湿润气候区，四季分明，光照充足，雨热同期。因山高谷深，小气候明显，降水变率较大，常发生春秋旱、夏涝的现象，降水主要集中在7—8月。境内大小河流共1 530条，呈树枝状分布。县内河流分属三大水系：沂河水系、汶河水系及弥河水系。沂源县有大型水库1座，中型水库1座，小型水库112座，沂源县地形地貌及河流水系如图1所示。

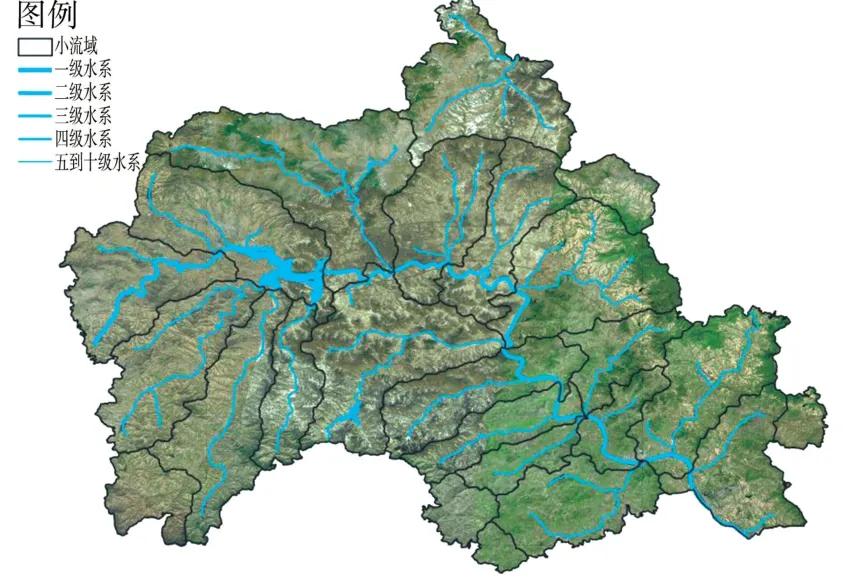
图1 沂源县地形地貌及河流水系

2 模型介绍及研究方法

2.1 SCS-CN模型介绍

SCS-CN模型是基于水量平衡方程和两个基本假设提出的经验模型。第一个假设：实际地表径流量与最大潜在径流量的比值等于实际入渗量与最大潜在蓄水量之比。第二个假设：初损量与最大潜在蓄水量成正比。

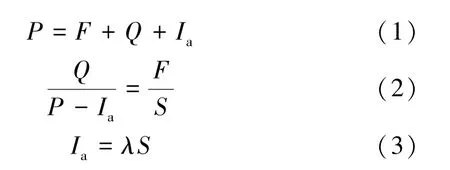
式中：Q为实际地表径流深，mm；P为降雨量，mm；F为实际入渗量，mm；Ia为降雨初损量，包括产流前植被截留雨量、土壤表层蓄水量和蒸发量等，mm；λ为初损率；S为最大潜在蓄水量，是集水区吸收和截留暴雨降雨能力的度量，mm。

由式（1）～式（3）可以建立SCS-CN模型地表径流量计算方程：

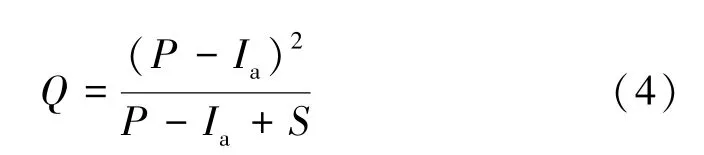
初损率λ受土地利用类型、植被截留、下渗等各种因素的综合影响，一般取值范围为［0～0.3］［11］。平均径流条件下，SCS-CN模型中λ取标准值0.2，即Ia=0.2S，得到SCS-CN经典计算公式：

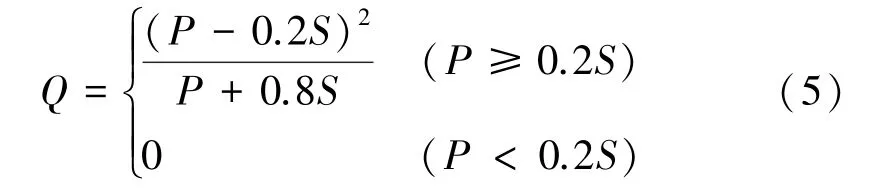
最大潜在蓄水量S为变量，其大小定性反映流域蓄水能力，且变化幅度可以很大，不便于取值，故引入无量纲的参数CN来推求S，S与CN值转换关系如下：

径流曲线数CN值是模型中用于描述降雨径流关系的一个无量纲的重要参数，其作为下垫面（包括地形、地质、土壤、植被和土地利用方式等）综合特征的定量描述，能够反映不同下垫面类型的产流能力［12］。CN值理论上介于0～100之间，实际条件下取值范围为30～98。CN值取决于土地利用现状、水文、土壤类型及前期土壤湿润程度。CN值越大，说明流域湿润状况越佳，地表的产流能力越强，地表蓄水量越小。CN=0时，S趋近于∞，表明降水全部下渗，地表无产流；CN=100时，S=0，表明流域无渗透，降雨全部转化为地表产流［13］。

2.2 CN值确定方法

采用SCS-CN模型进行径流模拟之前首先要确定参数CN值，CN值的确定方法分为查表法和反推法两种。查表法［14］，即根据SCS提供的CN值检索表基于土壤类型和土地利用确定CN值，该方法可能存在检索表中无法查找到中国某些特殊土地利用类型的问题。反推法，即通过SCS产流公式反推CN值，根据降雨径流实测资料率定CN值，主要包括平均值法、中值法、算术平均值法以及渐近线法，该方法需要研究区有一定年限的降雨径流数据［15］。沂源县小流域CN值采用查表法确定，并根据实测降雨径流数据利用反推法进行区域合理性验证。

查表法确定C N值首先要对流域土壤类型划分水文土壤组，SCS-CN模型中根据土壤水分下渗能力和土壤质地结构划分为A（透水）、B（较透水）、C（较不透水）、D（不透水）4类水文土壤组，见表1。

表1 水文土壤组［16］

通过查找CN值检索表获取研究区不同土地利用类型对应的CN值，运用ArcGIS软件，将研究区土壤类型图层和土地利用图层利用地理处理中的相交工具进行叠加，生成土壤-土地利用图层，该图层每一区域内只含有一种土地利用类型和土壤类型信息，并在每个小区域属性表中赋值其对应的CN值，最后通过对小流域内各小区域面积加权平均得到小流域CN值。

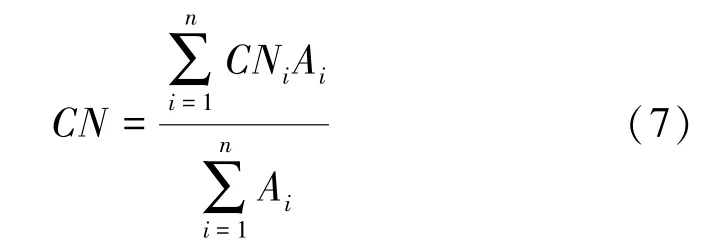
式中：CNi为土壤-土地利用图层每个小区域对应的CN值；Ai为每个小区域的面积；n为划分的小区域总数。

SCS-CN模型根据降雨前5 d的降雨量将前期土壤湿润程度（AMC）从低到高划分为三级：干旱（AMCI）、中等湿润（AMCⅡ）及湿润（AMCⅢ），见表2。

表2 前期土壤湿润程度分级

三级前期土壤湿润程度依次对应三种CN：CN1、CN2和CN3，CN1＜C N2＜CN3。查表法所得的CN值为CN2，可通过CN2求得CN1、CN3［17］。

由于反推法中的算术平均值法（利用实测降雨径流数据求出S，再求每一个S对应的CN值，取CN值的平均值为最终结果）计算结果合格率最高［15］，因此本文通过比较算术平均值法得出的CN值与查表法求得的C N值相近程度来检验查表法在研究区的适用性。

2.3 初损率λ优化方法

由SCS-CN模型地表径流量计算公式（式（4））可反推初损率λ的反算公式：

利用实测降雨径流资料通过反算公式可求得研究区初损率λ的取值范围，并计算变化范围内不同λ取值（包括中值、平均值等）［18-19］下的模拟径流深。本文以Nash公式中的模型效率系数E、标准均方根误差NRMSE、模型合格率作为判断依据。模型效率系数因其具有较好的检验能力被广泛用于水文模型效率检验［20］，反映模拟值与实测值1∶1的线性接近程度，模型效率系数E的取值范围为-∞～1，其值越接近1，表明模型的有效性越好，反之有效性越差。标准均方根误差NRMSE用来衡量模拟径流深与实测径流深之间的偏差，NRMSE值越大代表误差越大，模型精度越低。计算公式如下：

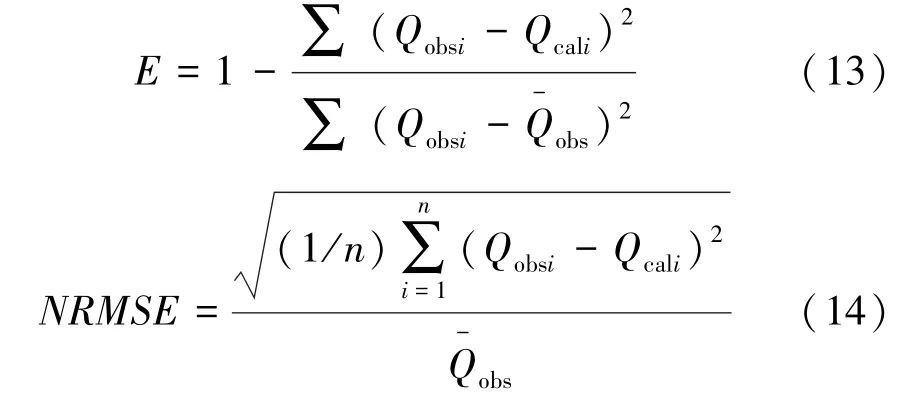
式中：Qobsi为实测径流深，mm；Qcali为模拟径流深，mm；obs为实测径流深的平均值，mm；n为总事件数。

模型合格率是水文预报中常用指标之一，首先统计出模拟径流深与实测径流深绝对误差≤2 mm或者相对误差≤30%的降雨场次，然后将该降雨场次占总降雨场次的百分数作为模型计算的合格率。

3 应用实例

3.1 沂源县小流域CN值确定

3.1.1 小流域C N值分布

沂源县土壤类型主要分为砂壤土、黏壤土、砂黏壤土、粉壤土、砂黏土，其中砂壤土占50%左右。土地利用类型主要有耕地、林地、草地、房屋建筑区等，林地分布于沂源县的北部、东部及中部地带，如图2和图3所示。沂源县土地利用类型见表3，沂源县一年中干旱期较长，主要农作物为小麦、玉米，耕地蓄水能力较强，故水文条件取好；沼泽地长期受积水浸泡，持水性强，透水性弱，故水文条件取差（水文条件差指下渗少径流多，水文条件好指下渗多径流少）。沂源县中等湿润条件（AMCⅡ）下CN值见表4。

图2 沂源县土地利用类型分布

表3 沂源县土地利用类型

表4 沂源县CN值

沂源县共分为24个小流域，通过对小流域内各土壤-土地利用叠加小区域面积加权求得各个小流域CN值，取值范围为52～82，其中较高CN值主要集中在沂源县南部，小流域CN值分布如图4所示。前期土壤湿润程度为干旱和湿润条件下的CN1、CN3可由式（8）和式（9）求得。

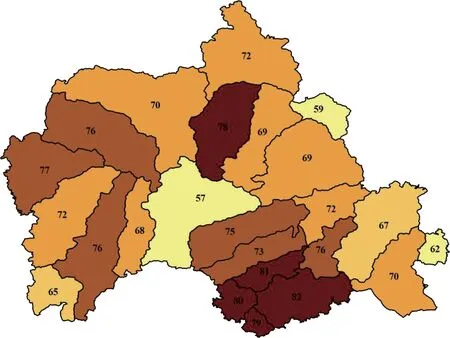
图4 沂源县小流域CN值分布

3.1.2CN值适用性验证

本文用于验证的实测降雨径流数据来源于高村河流域的朱家庄测站，选取前期土壤湿润程度为中等湿润（AMCⅡ）的场次通过反推法中的算术平均法求得的CN2值为70，查表法得出的CN2值为68，因此认为查表法所求CN值可靠，可以用于沂源县小流域。

3.2 初损率λ优化结果

本文选取沂源县朱家庄水文站及雨量站27场降雨径流数据用于初损率λ的优化，朱家庄测站位于高村河流域，控制流域面积31.4 km2，所在流域C N值为68，通过S与CN值转换关系（式（6））可求得最大潜在蓄水量S为119.53 mm，根据场次降雨数据运用反算公式确定高村河流域初损率λ的变化范围为0.05～0.50，平均值为0.20，中值为0.15，其中0.05～0.35的λ值约占85%，0.05～0.25的λ值约占66%，分别取λ=0.05、0.08、0.10、0.13、0.15、0.20、0.25、0.30，各场次降雨的模拟径流深计算结果见表5，各λ取值下的评判指标见表6。其中参数λ取标准值0.20时，E=0.760 0，λ=0.13时模型效率系数最大、标准均方根误差最小、合格率最高，故适合高村河小流域实际应用的初损率λ为0.13，亦可适用于沂源县其他下垫面相似流域。