基于滑模控制的牵引网低频振荡抑制方法*

胡颖新 宁志毫 兰 征 曾进辉 姜 飞 何 东

(1. 湖南工业大学电气与信息工程学院 株洲 412007；2. 国网湖南电力有限公司电力科学研究院 长沙 410036；3. 长沙理工大学电气与信息工程学院 长沙 410004)

1 引言

近年来，我国牵引网低频振荡现象频繁发生，振荡频率主要集中在3～7 Hz，可能导致动车组失去牵引能力，严重威胁电气化铁路系统的正常运行[1]。为防止低频振荡发生，提高牵引网供电可靠性，研究其抑制措施已迫在眉睫[2-4]。

目前许多专家学者针对牵引网低频振荡进行研究，通过分析低频振荡机理，主流认为牵引网的电气参数和动车组的控制参数两者不匹配是低频振荡现象发生的直接原因[5-9]。文献[5-6]通过频域阻抗建模分析了动车组的控制系统参数对低频振荡的影响，指出调整控制器的参数可以消除低频振荡现象，但并不能较好地抑制低频振荡发生。文献[7-8]推导了车网耦合系统的数学模型，通过稳定性判据指出了牵引网参数和动车组参数不匹配是低频振荡的主要原因。

为抑制低频振荡的发生，可通过改变牵引网或动车组电气参数两种方式。然而改变牵引网侧的参数存在一定的难度且不经济，改善动车组参数成为抑制低频振荡的主要手段。文献[9]研究认为，动车组网侧整流器为非线性、强耦合系统，其控制环节却采用线性PI控制器，不能较好完成非线性系统控制目标，造成牵引网低频振荡。文献[10-12]利用小信号模型分析，揭示出直流电压控制环的线性PI控制器使整流器呈现负阻尼特性，这是引发牵引网低频振荡的本质原因。文献[13-14]基于非线性控制的基本思想，将原PI控制器替换为自抗扰控制器，能够抑制牵引网低频振荡，但该控制器结构复杂，参数难以整定。

针对上述研究的不足，本文首先分析了牵引网低频振荡现象的机理，通过推导车网耦合系统的回比矩阵模型，绘制幅相频特性曲线理论分析低频振荡机理，确定牵引网低频振荡现象主要是由于动车组网侧整流器为非线性系统，却在控制环节采用线性PI控制器造成的；其次，从非线性角度出发，提出了将滑模控制替换原动车组网侧整流器的线性PI控制。最后，通过Matlab/Simulink仿真将所提控制策略与线性PI控制器对比分析，验证了所提控制策略在抑制低频振荡现象的正确性与有效性。

2 车网耦合系统低频振荡机理分析

2.1 车网耦合系统回比矩阵模型

车网耦合系统由牵引网系统和动车组组成，本文以CRH5型动车组[6,12]为研究对象，将车网耦合系统可以看作“源-负荷”模型，其等效电路模型如图1所示。

图1 车网耦合系统

牵引网侧用戴维南定理进行等效，由于CRH5型动车侧采用dq解耦控制，为分析系统完整特性，将牵引网侧阻抗变换至dq坐标系下，用Zsdq(s)表示为

负荷侧为动车组，CRH5动车组有5个动力单元，动车组牵引传动系统如图2所示。

图2 CRH5型动车组牵引传动系统

由于低频振荡发生在动车组升弓整备时刻，后端逆变器和交流电机处于闲置工作状态，为简化分析，以较大的负载电阻Rd来等效后端表示此时系统小电流运行工况[1-2]。动车组网侧整流器的等效拓扑结构如图3所示。

图3 网侧整流器拓扑结构

图3中，Rn和Ln分别为折算后的电阻和电抗，C是直流侧电容，Rd为忽略后端逆变器和电机情况下的负载等效电阻，从图2可知，单个动力单元都采用两重化脉冲整流器，所以单个整流器的负载电流为两重化整流器的一半，单个整流器的直流侧电容和等效电阻分别为1/2C和2Rd。

根据图3的拓扑结构，可得到其状态方程

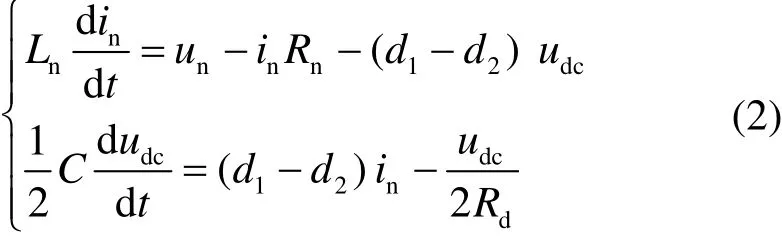
式中，d1和d2分别表示开关状态。

令en=eα，in=iα代入式(2)，状态方程解耦到dq系为

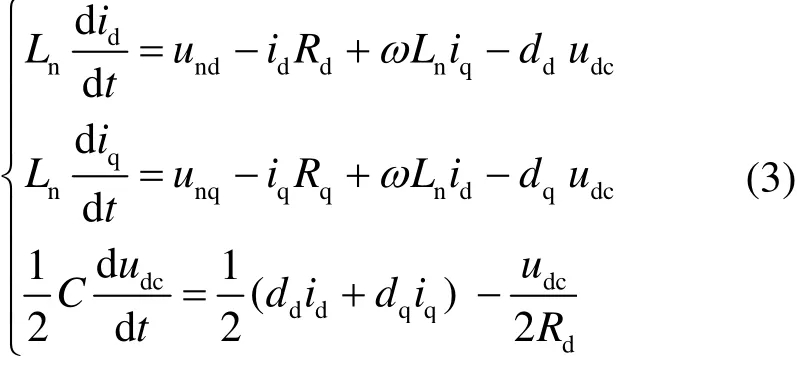
将式(3)在静态工作点下进行稳态值与小信号展开，并忽略稳态分量，得到式(4)

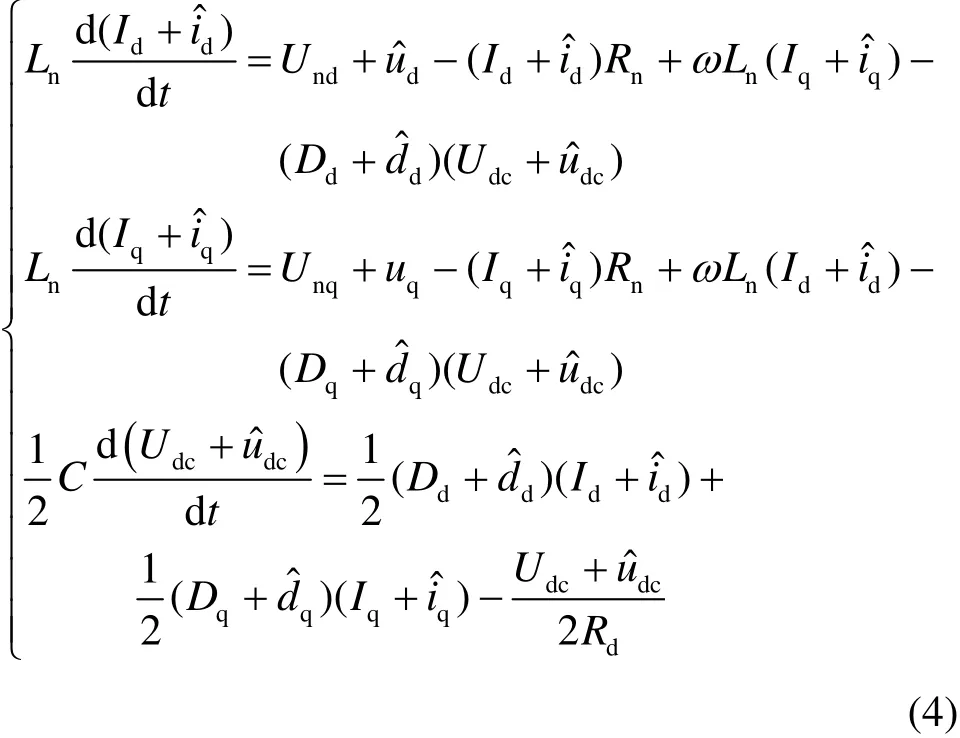
式(4)中存在小信号的乘积项，这些项的存在体现了该整流器系统的非线性特性。当车网耦合系统同时投入多台同型号动车组，这些非线性项的相互耦合影响，从而使得网侧整流器呈现出非线性、多变量、强耦合特性，线性PI控制器已无法满足控制要求，给系统稳定性带来巨大挑战。

在忽略了两个小信号值乘积的稳态值和无穷小值的情况下，可以得到式(5)整流器数学矩阵模型。

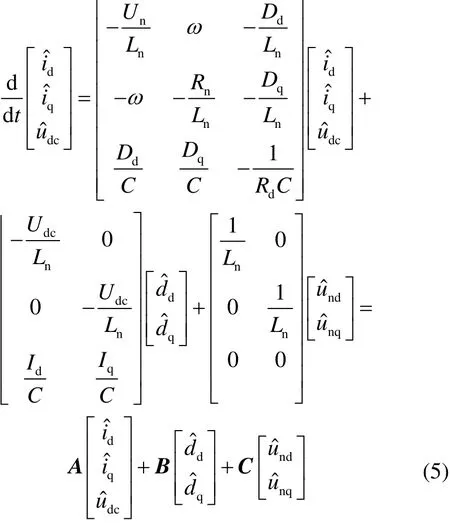
式中，A、B、C为系数矩阵。

式(5)经拉普拉斯变换，可得

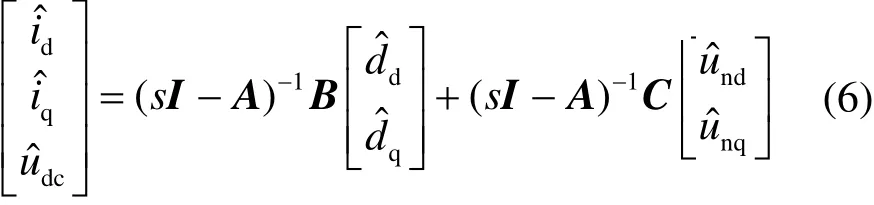
式中，I为单位矩阵；A、B、C为系数矩阵，式(6)为单相PWM整流器的广义dq解耦小信号模型，其中dˆd和dˆq根据不同的控制策略确定，文献[8]已针对CRH5型号动车组进行推导。

CRH5型号动车组dq解耦小信号模型为

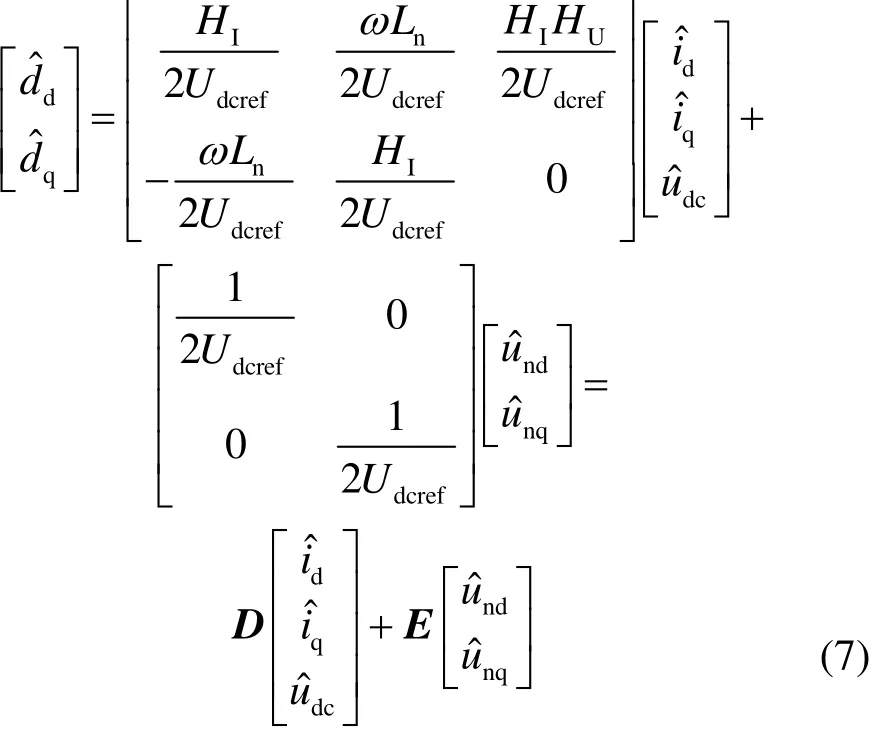
式中，HU和HI是PI控制器的传递函数；D、E为系数矩阵。

将式(7)代入式(6)可得单台整流器的dq系下的状态方程

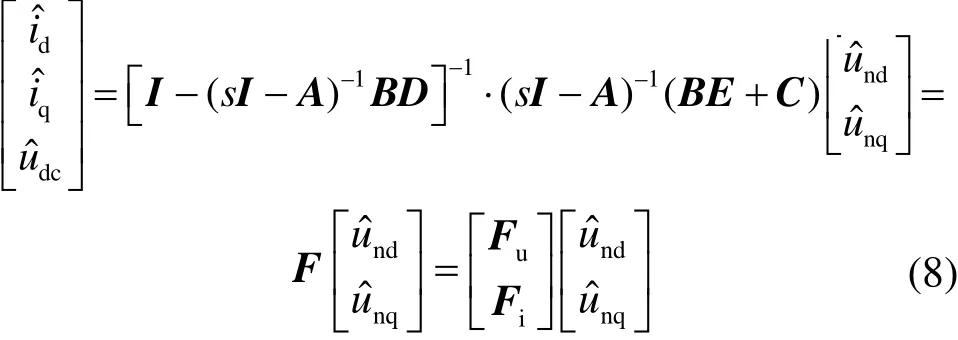
式中，Fi是一个2×2分块矩阵；Fu是1×2的分块矩阵。

单个整流器的输入导纳可以表示为

由于CRH5动车组有5个动力单元，每个动力单元均是两重化整流，当n列动车组投入时，其输入导纳矩阵为

在dq坐标系下，多列动车组输入导纳YLdq(s)的矩阵形式为

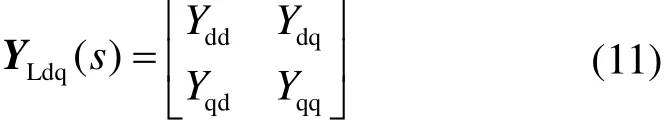
根据式(1)和式(11)，车网耦合系统回比矩阵Ldq(s)为

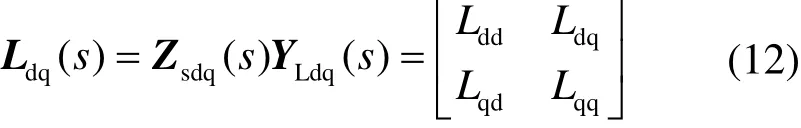
2.2 基于改进sum-范数判据的稳定性分析

通过第2.1节的回比矩阵模型，结合文献[15]所提出的sum-范数判据，研究牵引网低频振荡产生机理，其改进sum-范数判据为

式(13)为两个子判据的并集，判据指出当两子判据均在0 dB线上，才认定级联系统不稳定，其余情况认为级联系统是稳定的，分析结果保守性小，与实际情况更接近。通过调整式(10)中动车组的台数n来绘制不同工况的幅频特性曲线。

通过幅频特性曲线分析车网耦合系统稳定性，车网系统临界稳定点在5列动车组和6列动车组之间，图4a为5列动车组同时投入，子判据都在0 dB线以下，此时系统处于稳定状态。图4b为6列动车组同时投入，两子判据均在0 dB线以上，曲线在频率为769 rad/s时，峰值为1.47 dB，由判据可知，此时系统处于不稳定状态。图4c为7列动车组同时投入，两条曲线在一定频率段内，远在0 dB线以上，此时系统已处于失稳的状态。当改变系统控制策略时，系统回比矩阵也会随着改变，进而影响系统的稳定性。分析幅频特性曲线可知，牵引网低频振荡主要与牵引网侧的等效阻抗和动车组侧的等效导纳有关。

图4 车网耦合系统稳定性分析

因此，抑制低频振荡的发生，可改变牵引网侧的等效阻抗和动车组侧的等效导纳，改变牵引网侧的等效阻抗存在一定的难度，且不符合经济性的原则，从而本文以改善动车组侧的等效导纳为目标，通过优化动车组网侧整流器的控制策略来增强系统稳定性，达到抑制低频振荡的目的。

3 车网耦合系统低频振荡抑制方法

由上文分析可知，原电压外环的线性PI控制器无法较好地满足网侧非线性整流器的控制要求，是引发低频振荡的主要因素。因此本文从非线性角度，根据滑模控制[16-17]的基本思想，提出了用滑模控制器替换原动车组电压外环的线性PI控制器，实现对低频振荡的抑制。

3.1 滑模电压控制器设计

结合整流器控制目标要求，并使系统性能具有更好的优越性，选取直流母线电压udc偏差和udc的一阶导数udc′=dudc/dt作为滑模函数。mudc和mudc′分别表示udc和udc′的偏差值。

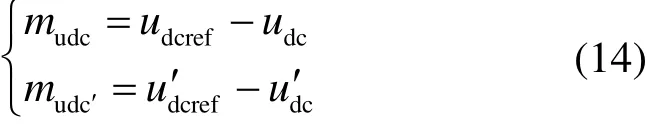
建立与udc、udc′对应的滑动模态η为

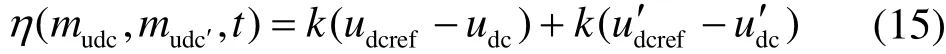
式中，k为放大增益，将其代入状态方程可得idref的表达式

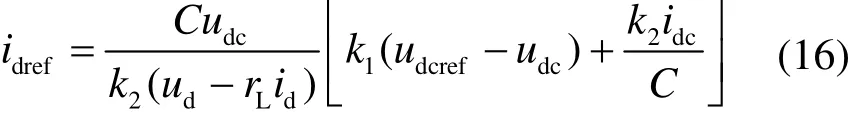
其电压外环控制器的结构框图如图5所示。

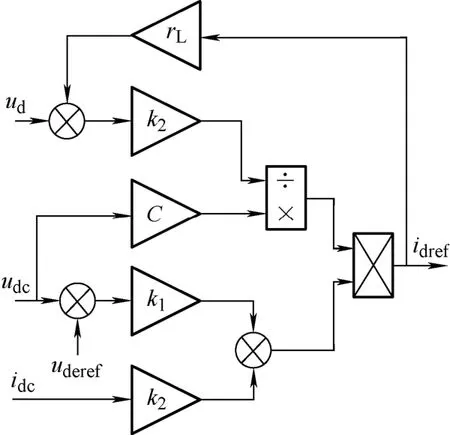
图5 电压外环滑模控制器

当动车组刚投入系统时，系统受到大扰动冲击，使得系统输出值与预设值存在较大偏差，影响系统稳定。为缓解此现象，将电压外环采用滑模控制，可使控制量直流侧输出电压在所设定的滑模面周围平滑迅速调节，直至达到稳定。其次，系统参数及扰动对滑模面没有影响，使系统具有更强的鲁棒性，实现随着系统误差大小的变化而变化。

3.2 电流内环控制器设计

电流控制器框图如图6所示，分别对id、iq解耦控制，Kp与Ki分别为比例系数与积分系数。

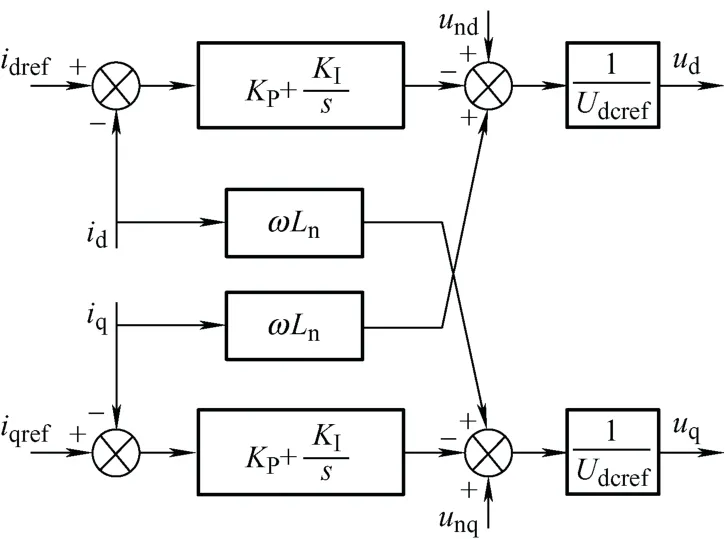
图6 电流内环控制器

根据图6得到dq坐标系下的电压控制量为

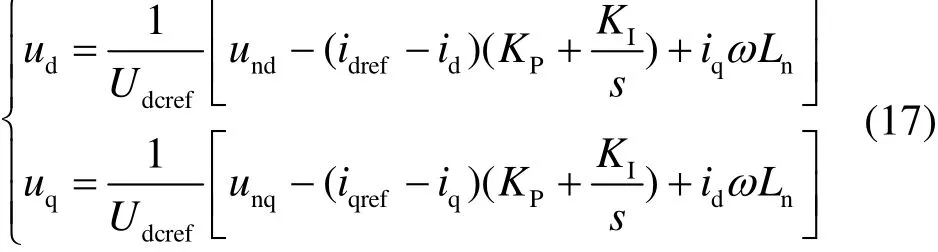
式中，iqref等于零，而idref可通过图6所示的电压控制回路获得，Udcref是直流侧电压参考值。

3.3 动车组网侧整流器控制框图

动车组网侧整流器控制框图如图7所示。

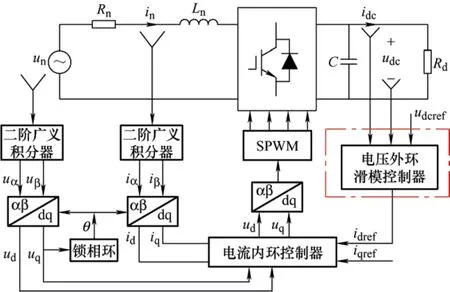
图7 动车组网侧整流器控制框图

由图7可知，CRH5动车组网侧整流器基于滑模控制的控制策略由电压外环滑模控制器、电流内环控制器、二阶广义积分器和锁相环四部分组成。通过电压外环滑模控制器使直流侧电压稳定到其参考值，电流dq解耦控制实现网侧电压和电流同相，使其单位功率因数运行，实现对动车组网侧整流器的控制。

4 车网耦合系统仿真分析

在Matlab/Simulink环境下建立了车网耦合系统仿真，如图8所示，分别将提出的基于滑模控制策略与基于线性PI控制策略进行了多工况仿真对比分析。

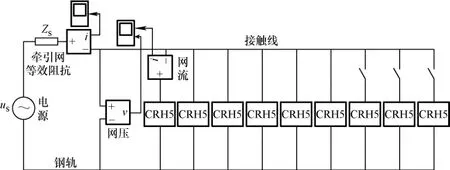
图8 车网系统仿真模型

图9a和9b分别是单列动车组和6列动车组接入牵引网的仿真波形。由图9a可以看出单列动车组运行时，动车组侧的电流、电流和直流侧电压均稳定。然而，6列动车组接入牵引网时，就出现牵引网低频振荡现象。在图9b的左侧，交流电压波形的包络面在4.5 Hz附近振荡，其振幅在2 600～3 200 V波动，直流电压的振荡频率为4.5 Hz。直流侧和交流侧的电压同时波动，动车组侧交流电流的总谐波失真(THD)达到78.59%，如图9b右侧所示。此外，高次电流谐波含量集中在45.5 Hz和54.5 Hz。

图9c为当6列动车组接入牵引网时基于滑模控制策略下动车组侧的电压和电流波形。显然，电压和电流的振荡都被抑制，直流侧电压稳定在3 000 V，电压波动为35 V。即在基于滑模控制策略下，车网耦合系统是稳定的，同时动车组侧交流电流的总谐波失真(THD)降低到4.8%。

图9 动车组接入时电压、电流波形

为验证所提控制方法对低频振荡的抑制效果，先将5列动车组同时投入运行，控制方式为PI控制，且使系统等幅振荡，在2 s时刻将控制方式切换至滑模控制，动车组侧电气量仿真波形如图10a所示，直流环节电压经过0.2 s调整后恢复至稳定。

在PI控制下使系统失稳后，在2 s时刻将控制方式切换至滑模控制，动车组侧电气量仿真波形如图10b所示，直流环节电压经过1.8 s调整后恢复至稳定，说明本文提出的基于滑模控制策略在不同工况下，较好地抑制牵引网低频振荡现象。

图10 系统不同工况下滑模控制性能

图11为当动车组接入牵引网数量变化时两种不同控制方法之间的系统性能比较。先投入4列动车组正常运行后，在2 s、4 s、6 s时刻增投一列动车组，动车侧电气量波形如图11所示。

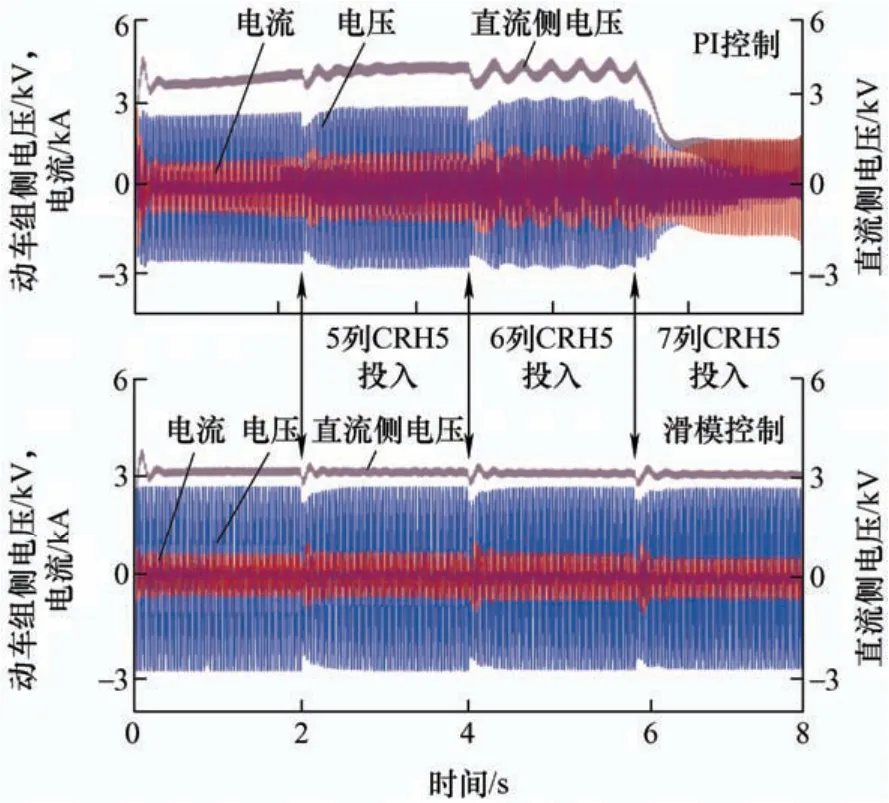
图11 增投动车组时电压、电流波形

图11上半部分为PI控制方式的仿真波形，仿真结果表明车网耦合系统发生低频振荡为6列动车组，与第2.2节理论性分析结果一致。在2 s时刻同时投入4列动车组，此时直流侧电压波形出现振荡现象，但振荡时间不长，系统能够在一定时间内重新恢复稳定；在4 s时刻增投一列动车组，动车侧电压、电流和直流侧电压波形均出现了振荡现象，振荡持续，此时系统已不稳定；在6 s时刻再增投一列动车组，此时车网耦合系统已失稳。

图11下半部分为在滑模控制方式的仿真波形，当动车组投入数量增多时，动车组电气量均无振荡现象，系统保持稳定，进一步验证了牵引网低频振荡是由于线性PI控制无法达到非线性系统的控制要求，仿真结果与理论分析一致。

图12为基于滑模控制的车网耦合系统在动车组接入牵引网数量变化时电压、电流波形。系统先同时投入7列动车组系统正常运行后，每隔2 s再增投一列动车组，增投动车组数达到15列，动车组侧电气量波形如图12所示。

图12 基于滑模控制下的动车组时电压、电流波形

由图12可知，网侧整流器采用滑模控制的车网耦合系统临界稳定点在14列动车组和15列动车组之间。前14列动车组每次投入车网耦合系统时动车组侧电气量经过0.06 s后能平稳地到达稳定状态，当15列动车组投入时，系统出现失稳。相比于原动车组网侧整流器采用PI控制，本文所提控制方法较好地维持了车网耦合系统的稳定性，明显抑制了低频振荡现象，验证了所提方法的正确性与有效性。

5 结论

为解决牵引网低频振荡现象，本文分析了牵引网低频振荡机理，提出了基于滑模控制的低频振荡抑制方法，结论如下。

(1) 通过改进sum-范数判据验证了牵引网耦合低频振荡主要与牵引网侧的等效阻抗和动车组侧的等效导纳有关。传统线性PI控制器已无法较好地实现动车组非线性网侧整流器的控制目标要求，对外部扰动没有良好的抑制能力。

(2) 网侧整流器电压外环采用滑模控制能够有效地抑制了低频振荡现象，车网耦合系统临界稳定点提升至在14列动车组和15列动车组之间，使系统具有更强的鲁棒性，对电气化铁路负荷波动较大的场合具有良好的控制性能。