基于高分六号卫星红边波段的森林蓄积量遥感反演<br/>——以西宁市针叶林为例*

基于高分六号卫星红边波段的森林蓄积量遥感反演
——以西宁市针叶林为例*

2022-05-20任庆福

中国农业气象 2022年5期

任枫，王琦，杨佳，任庆福**

（1.西安绿环林业技术服务有限责任公司，西安 710048；2.广东省科学院生态环境与土壤研究所，广州 510650；3.航天宏图信息技术股份有限公司，北京 100089）

森林蓄积量是指森林中全部树木材积的总和，它是反映一个地区森林资源的丰富程度、衡量森林生态环境优劣、进行森林经营和采伐利用的重要依据[1]。传统森林蓄积量的估算是通过林分调查，建立材积方程，进而推算区域森林蓄积量，往往存在工作量大、效率低下、成本高等问题。随着遥感技术的快速发展，森林蓄积量的遥感反演已成为获取区域森林蓄积量的主要手段[2]。目前，光学遥感的森林蓄积量反演，多数研究采用Landsat TM/ETM/OLI[3-4]、MODIS[5]、SPOT5[6]、资源三号[7]、GF1/2[8-10]等卫星载荷，通过提取与蓄积量相关的因子（如地形因子、光谱信息、植被指数、影像纹理等）建立模型进行反演，因此，在建模过程中，敏感因子的选择就成为影响蓄积量反演精度的关键因素。

一直以来，红光波段和近红外波段常被作为指示植被生长状况的敏感波段，但有研究指出，介于红光与近红外波段之间的红边波段，对植被叶绿素更加敏感[11-13]。受卫星载荷的波段限制，红边波段在植被监测方面的研究局限于基于地物光谱仪[14-15]。近年来，有较多的卫星载荷（如美国的WorldView-2/3、欧空局的Sentinel-2、德国的RapidEye等）增加了红边波段，基于红边波段的森林蓄积量遥感反演的研究随之也不断问世[16-18]。这些研究多以Sentinel-2为遥感数据源，以模型的适用性评价为主要研究目标，极大丰富了蓄积量反演研究的数据源和模型方法，而关于红边波段对蓄积量反演精度的影响缺乏深入研究，加之光学遥感影像数据的有效性易受云雾影响，因此，仅仅以Sentinel-2为数据源极大限制了红边波段在森林蓄积量反演方面的研究与应用。国产高分六号卫星的宽幅影像（GF6-WFV）是中国首颗带有红边波段的中高分辨率影像。但目前，基于GF6-WFV红边波段的研究主要集中在植被识别及分类[19-24]、森林扰动[25]等方面，在森林蓄积量反演方面的研究未见报道。因此，基于GF6-WFV卫星红边波段的森林蓄积量反演研究，对于明确红边波段对森林蓄积量反演的作用以及拓展国产高分卫星的应用具有重要的理论指导意义。

西宁市地处黄土高原与青藏高原交界地带，在生态环境方面具有极其重要的地位。但该地区存在生态防护功能差、森林生态系统脆弱、林地质量差等问题[26-27]，迫切需要对全区的森林蓄积量进行动态监测。本研究以GF6-WFV为遥感数据源，结合西宁市DEM及2014年森林资源二类调查数据，从光谱特征、植被指数、地形因子、影像纹理4个方面选取了蓄积量反演的自变量，并在此基础上采用多元线性回归、随机森林模型，研究红边波段对西宁市针叶林蓄积量遥感反演精度的影响，以期为西宁市森林蓄积量的区域动态监测提供方法借鉴，为红边波段在森林蓄积量遥感反演中的应用提供理论依据，为拓展国产高分六号遥感卫星的应用提供新的途径。

1 资料与方法

1.1 研究区概况

研究区位于青海省东部的西宁市，地理位置介于100°52'7″-101°54'58″E、36°13'40″-37°28'9″N，平均海拔3127.8m。研究区地处黄河一级支流湟水河中游，是黄土高原向青藏高原的过渡地带，地形复杂，以川水、浅山、脑山3种地形为主，具有典型的干旱高原大陆性气候，年平均气温为5.8℃，极端最低气温为-26℃，极端最高气温为41℃，无霜期约160d。年平均降水量368mm，集中于7-9月；年蒸发量为1100mm，年日照时数2600h。研究区分布的主要乔木树种有青海云杉（Picea crassifolia）、落叶松（Larix principis-rupprechtii Mayr）、油松（Pinus tabulaeformis Carr.）、祁连圆柏（Sabina przewalskii）、白桦（Betula platyphylla Suk）、青杨（Populus cathayana Rehd.）、旱柳（Salix matsudana Koidz）等。

1.2 数据来源及预处理

1.2.1 遥感影像数据及预处理

遥感影像数据来源于自然资源卫星遥感云服务平台（http://www.sasclouds.com/chinese/normal/），选用2019年8月15日覆盖西宁市的高分六号卫星宽幅影像（简称GF6-WFV），其卫星具体参数见表1。采用国产遥感处理软件PIE-Basic6.0（https://www.piesat.cn/product/PIE-Basic/index.htMLR）对GF6-WFV影像进行辐射定标、几何校正、大气校正等预处理，最终得到各波段的地表反射率数据。其中，影像的几何校正处理所需的高程数据来源于地理空间数据云（http://www.gscloud.cn/）的GDEMV2 30M分辨率数字高程数据集。从该数据集中下载覆盖GF6-WFV整幅影像（93°00'00″- 103°00'00″E、35°00'00″-40°00'00″N）的DEM数据，DEM的分幅数据拼接采用ArcGIS10.2软件完成。

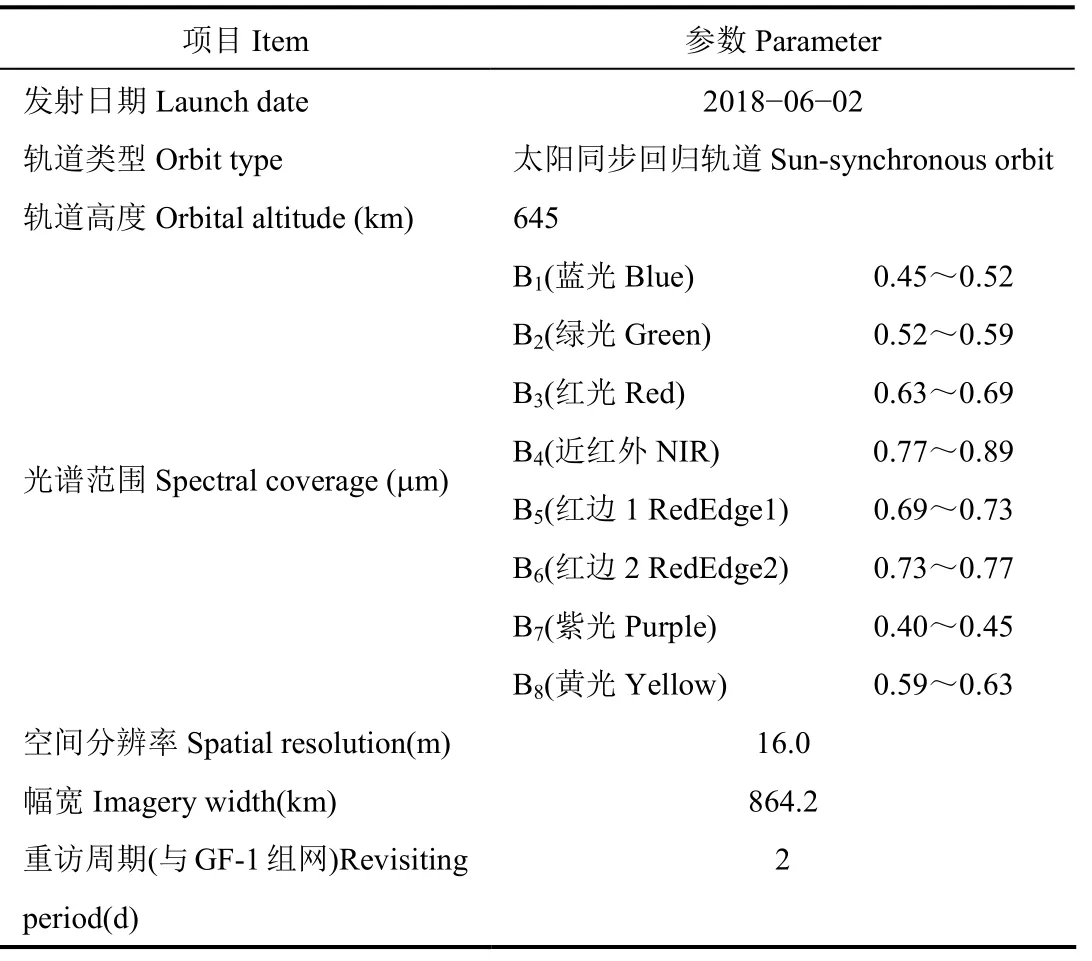
表1 GF6-WFV卫星参数Table 1 The satellite parameters of GF6-WFV

1.2.2 针叶林蓄积量

针叶林蓄积量的地面验证数据来源于西宁市2014年森林资源二类调查数据。由于研究区地处西北干旱区，针叶树种生长速度较慢，且与影像获取时间滞后在一个龄级（10a）内，因此，忽略影像获取时间与蓄积量调查时间的滞后效应。利用三倍标准差分析方法剔除针叶林蓄积量异常的调查小班，共获得503个调查小班的针叶林蓄积量数据，得到西宁市针叶林调查小班（平均胸径在5cm及以上）的分布（图1）。

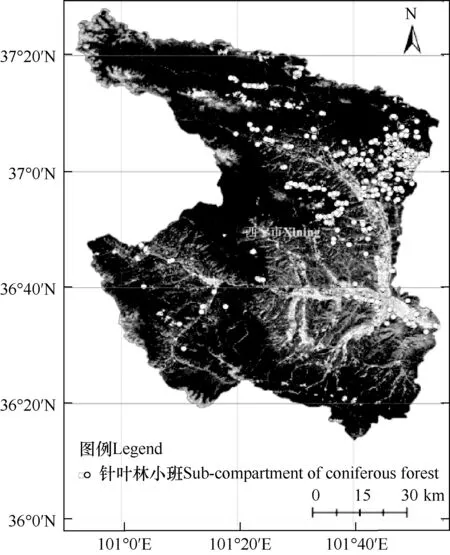
图1 GF6-WFV影像及针叶林调查小班分布Fig.1 GF6-WFV imagery and the sub-compartments of coniferous forest in study area

1.3 自变量选取与确定

1.3.1 植被指数

以GF6-WFV影像前6个波段（即表1中的B1、B2、B3、B4、B5和B6）的地表反射率作为单波段反射率变量。选取归一化植被指数（NDVI）、比值植被指数（RVI）、增强植被指数（EVI）和土壤调节植被指数（SAVI）4个常规植被指数，在此基础上选取基于红边波段的2个植被指数即MTCI指数[28]和NDREI指数[29]，作为针叶林蓄积量反演的植被指数变量，具体计算式见表2。

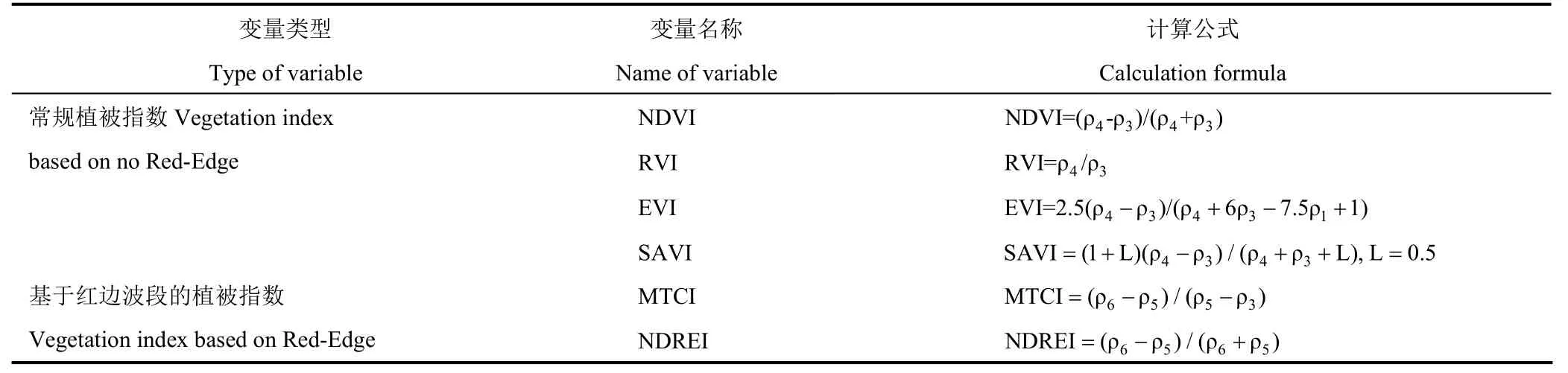
表2 植被指数计算公式Table 2 The formula of different vegetation index

1.3.2 地形及纹理特征变量

选取坡度（Slope）、坡向（Aspect）作为地形因子变量。影像纹理特征的描述采用灰度共生矩阵方法（Gray-Level Co-occurrence Matrix, GLCM），选取均匀性（H）、异质性（D）、对比度（CT）、能量（ENG）、相关性（CR）、信息熵（ENT）6个指标来刻画GF6-WFV影像的纹理特征。

采用滑动窗口法（窗口大小3×3）分别计算GF6-WFV影像前6个波段的6个纹理特征，得到研究区内36张纹理特征变量的分布图，然后分别计算各调查小班范围内的纹理特征变量的平均值，得到503个调查小班对应的36个纹理特征变量值。

1.3.3 自变量分组与确定

（1）将选取的6个单波段反射率变量、6个植被指数变量、2个地形因子变量以及36个纹理特征变量有重复地分为无红边波段处理（No Red-Edge）和加入红边波段处理（Red-Edge Added）两组。

在无红边波段的处理中，自变量包括ρ1、ρ2、ρ3、ρ4、NDVI、RVI、EVI、SAVI、Slope、Aspect以及影像前4个波段对应6个纹理指标的24个纹理特征变量；在加入红边波段的处理中，其自变量是在无红边波段处理的自变量基础上，增加GF6-WFV影像第5、第6红边波段相关的自变量，即ρ1、ρ2、ρ3、ρ4、ρ5、ρ6、NDVI、RVI、EVI、SAVI、Slope、Aspect以及影像前6个波段对应6个纹理指标的24个纹理特征变量。

（2）采用主成分分析法（Principal Component Analysis）对两组处理的纹理特征变量进行降维处理，获得新的变量，作为纹理特征的备选变量。

（3）分别将两组处理的备选自变量与针叶林蓄积量建立逐步回归方程，根据AIC最小准则，最终确定两组处理的自变量。

1.4 模型构建和检验

1.4.1 模型选取

从总体样本（503个调查小班的蓄积量及对应自变量）中随机抽取75%的数据作为模型的训练样本，其余25%作预测样本。选取线性、非线性模型分别对无红边波段（No Red-Edge）、加入红边波段（Red-Edge Added）的两组处理进行蓄积量反演，模型的构建及精度评价通过Python语言实现。

线性反演模型采用多元线性回归模型（MLR）,非线性反演模型采用随机森林模型（RF）。

随机森林模型是一种基于决策树的机器学习算法[30]，它是在决策树的基础上，利用bootstrap方法从训练集 X = { x1, x2,… , xn}中有放回的多次重复采样，然后结合对应的目标值对这些样本训练模型，在训练结束之后，对未知样本的预测可以通过简单多数原则确定检验样本的反演结果。

1.4.2 模型构建及精度评价

（1）基于两组处理的训练样本，分别对MLR、RF模型的参数进行训练，以决定系数为代价函数，得到各模型的最优参数。

（2）将得到的最优参数带入MLR、RF模型，对两组处理的预测样本进行蓄积量的预测。

（3）通过十折交叉验证方法，分别将两组处理的MLR、RF模型预测的蓄积量与预测样本的蓄积量进行对比，计算两者之间的决定系数（R2）和均方根误差（RMSE），以衡量模型反演的性能及精度。计算式为

式中，n为预测样本个数，yˆi为模型预测的蓄积量（m3·hm-2）；yi为预测样本的蓄积量（m3·hm-2）。

2 结果与分析

2.1 纹理特征变量降维

无红边波段处理（No Red-Edge）的24个纹理特征变量包括GF6-WFV影像前4个波段（B1、B2、B3、B4）对应的6个纹理指标（H、D、CT、ENG、CR、ENT）；加入红边波段处理（Red-Edge dded）的36个纹理特征变量包括GF6-WFV影像前6个波段（B1、B2、B3、B4、B5、B6）对应的6个纹理指标（H、D、CT、ENG、CR、ENT），采用主成分分析法分别对两组处理的纹理特征变量进行降维处理，选择方差累计贡献率大于95%的主成分变量代替原有的纹理特征变量。

经计算，无红边波段处理的纹理特征变量中提取到9个主成分（记为P1N, P2N, …, P9N），其方差累计贡献率为95.59%（表3）。对主成分中24个变量的系数进行排序，选取系数最大的前3个变量，对9个主成分逐个分析，从波段方面来看，第1、2、3个主成分的方差贡献率分别为45.44%、19.78%、10.06%，分别解释了B2、B3、B4波段的纹理特征；纹理指标以异质性（D）、均匀性（H）、能量（ENG）以及信息熵（ENT）为主。

表3 无红边波段处理的纹理特征变量主成分分析结果Table 3 The PCA result of the texture feature variables for the No Red-Edge treatment

加入红边波段处理的纹理特征变量中提取到13个主成分（记为P1A, P2A, …, P13A），其方差累计贡献率为95.45%（表4）。加入红边波段之后，第1主成分的前3个变量与无红边波段的处理一致，但其方差贡献率降为36.09%；第2主成分的方差贡献率为18.38%，且增加了B6波段的均匀性（H）；第3主成分则反映了B5波段的纹理特征，以能量（ENG）、均匀性（H）、异质性（D）为主要指标，其方差贡献率为10.27%。因此，对于无红边波段处理的纹理特征变量，以9个主成分（即P1N, P2N, …, P9N）替代原有的24个特征变量；对于加入红边波段处理的纹理特征变量，则以13个主成分（即P1A, P2A, …, P13A）替代原有的36个特征变量。

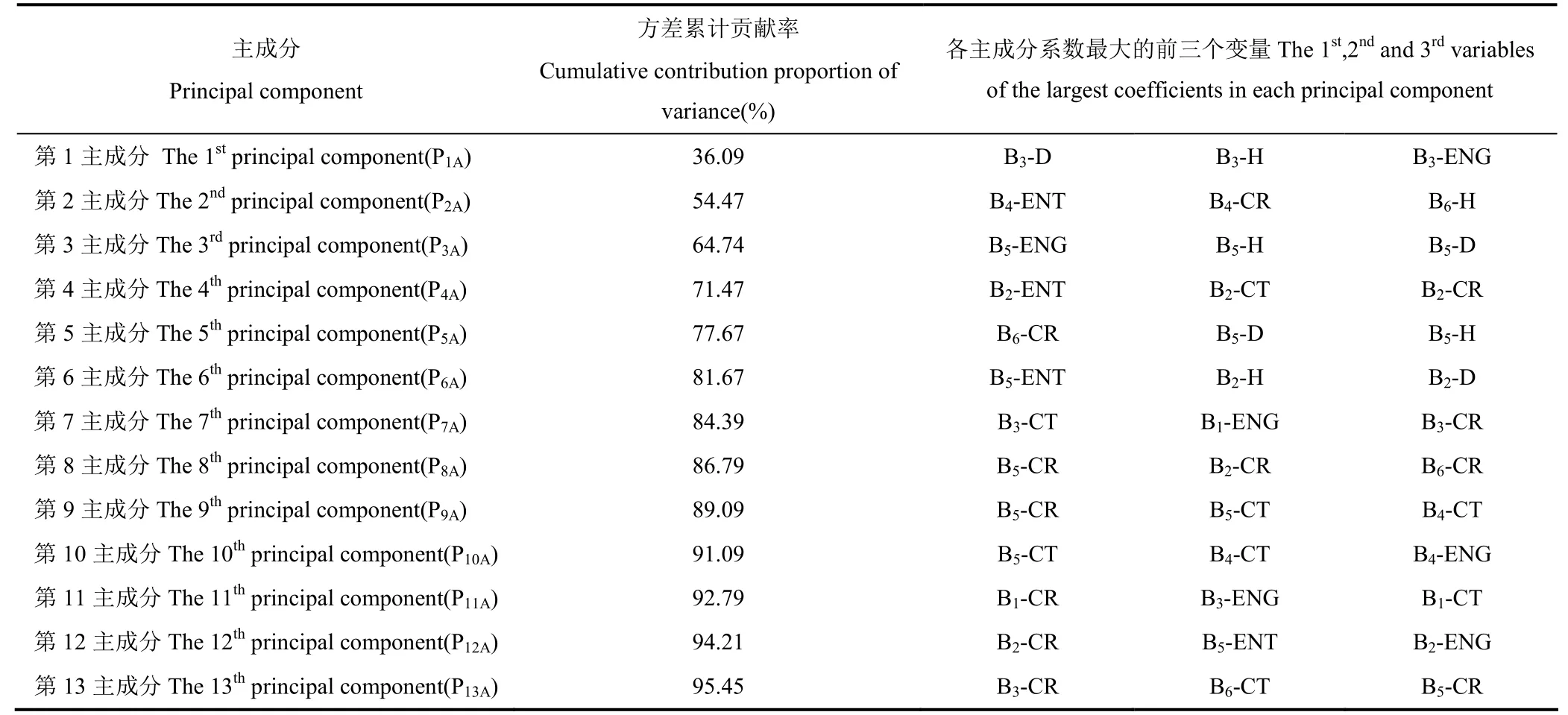
表4 加入红边波段处理的纹理特征变量主成分分析结果表Table 4 The PCA result of the texture feature variables for the Red-Edge Added treatment

2.2 自变量筛选

无红边波段处理包括4个单波段地表反射率变量（1ρ、ρ2、ρ3、ρ4）、4个植被指数变量（NDVI、RVI、EVI、SAVI）、2个地形因子变量（Slope、Aspect）以及9个纹理主成分变量（P1N, P2N, …, P9N）共19个备选自变量；加入红边波段处理包括6个单波段地表反射率变量（1ρ、ρ2、ρ3、ρ4、ρ5、ρ6）、6个植被指数变量（NDVI、RVI、EVI、SAVI、MTCI、NDREI）、2个地形因子变量（Slope、Aspect）以及13个纹理主成分变量（P1A, P2A, …, P13A）共27个备选自变量。分别将各备选自变量与针叶林蓄积量建立逐步回归方程，依据AIC最小准则，得到两组处理最终筛选出的自变量（表5）。表5中，无红边波段处理筛选出11个变量（ρ2、ρ3、ρ4、NDVI、SAVI、Slope、P1N、P2N、P4N、P5N、P9N），而加入红边波段处理筛选出13个变量（1ρ、ρ2、ρ5、MTCI、Slope、P1A、P2A、P3A、P5A、P6A、P7A、P9A、P11A）。

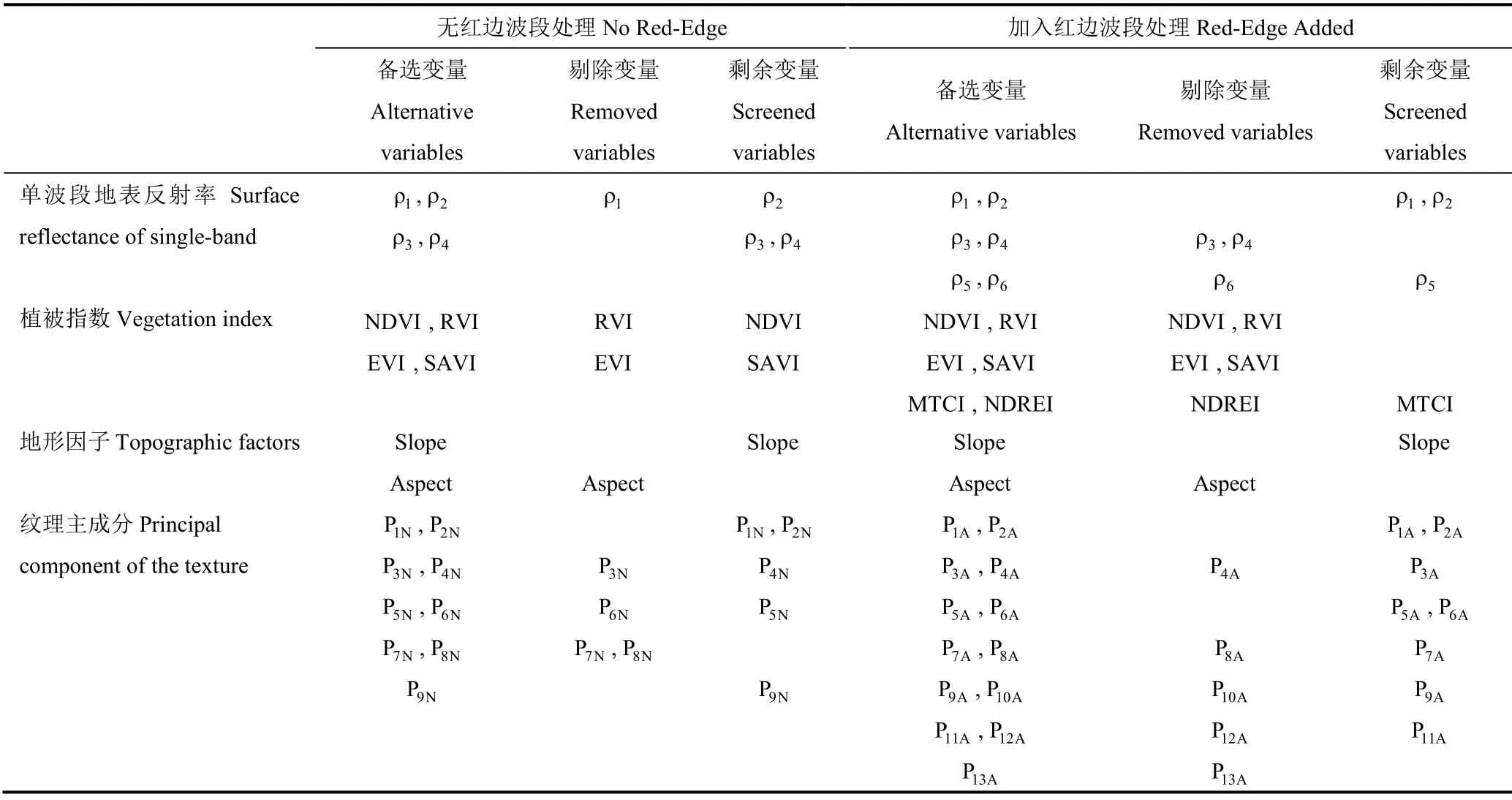
表5 无红边波段和加入红边波段处理下筛选出的反演变量Table 5 The screened variables for retrieval under the No Red-Edge and the Red-Edge Added treatment

从单波段地表反射率来看，两组处理均包括B2波段的地表反射率；植被指数方面，No Red-Edge处理筛选出了NDVI、SAVI，而Red-Edge Added处理只有MTCI；纹理方面，No Red-Edge处理的纹理主成分包括了第1、2、4、5、9主成分，结合表3可知，纹理指标以异质性（D）、均匀性（H）、能量（ENG）以及信息熵（ENT）为主，波段集中在B3、B4；Red-Edge Added处理的纹理成分包括了第1、2、3、5、6、7、9、11主成分，结合表4可知，加入红边波段后，B5波段的纹理特征出现，且以异质性（D）、均匀性（H）和信息熵（ENT）为主要指标。

2.3 模型构建及其反演结果

2.3.1 多元线性模型

利用75%的训练样本，根据无红边波段（No Red-Edge）、加入红边波段（Red-Edge Added）筛选出的自变量，分别与针叶林蓄积量构建多元线性模型，得到两组处理的多元线性回归方程为

式（3）、式（4）中，Vno、Vadd分别为No Red-Edge、Red-Edge Added处理反演的蓄积量（m3·hm-2）。

根据训练样本建立的多元线性回归模型，两组处理的显著性均小于0.001，方程的决定系数（R2）均大于0.55，且Red-Edge Added处理的决定系数有所提高。

2.3.2 随机森林模型

利用75%的训练样本，根据无红边波段（No Red-Edge）、加入红边波段（Red-Edge Added）两组处理筛选出的自变量，分别与针叶林蓄积量构建随机森林模型。关键的模型参数主要包括决策树个数、决策树最大深度、决策树的最大特征数、叶子节点的最小样本个数和最大叶子节点数5个参数。

以决定系数为代价函数，经过多次试验，得到各参数的最优值（表6）。结果表明对于训练样本，两组处理的R2均在0.85以上，且Red-Edge Added处理的决定系数略高于No Red-Edge处理。

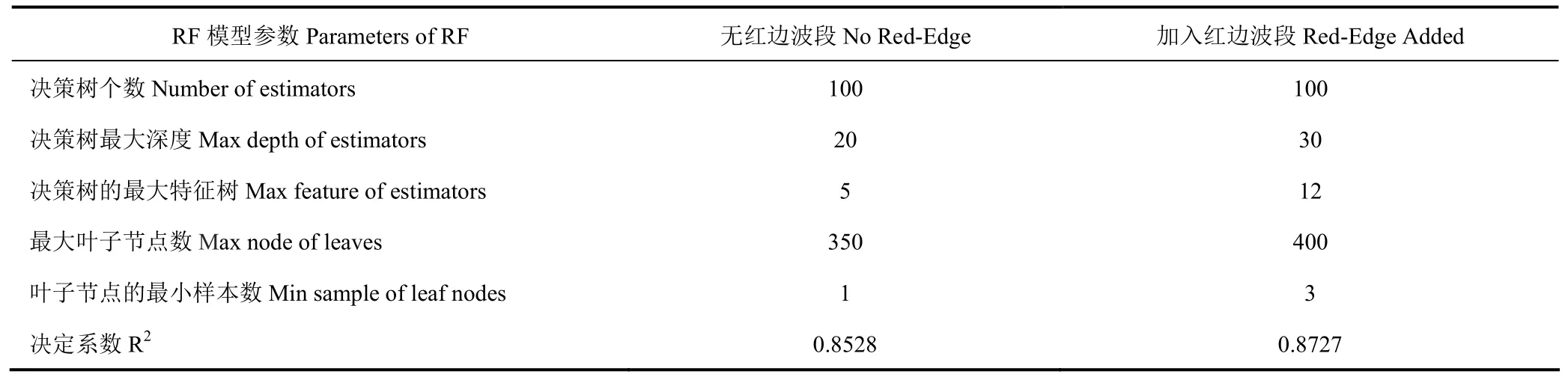
表6 无红边波段和加入红边波段处理下随机森林模型参数优化结果Table 6 The parameter optimization results of rand forest model under the No Red-Edge and the Red-Edge Added treatment

2.3.3 模型验证

利用25%的预测样本，将No Red-Edge、Red-Edge Added两组处理筛选出的自变量，代入到构建的MLR、RF模型中，得到两组处理各模型的蓄积量反演值。将十折交叉验证结果平均，得到西宁市针叶林蓄积量的遥感反演结果与观测值之间的关系图（图2）。由图2可见，两组处理的MLR、RF模型反演的蓄积量结果与观测值之间的相关性，其显著性均小于0.001；从散点图的分布来看，MLR模型的反演结果较离散，而RF模型的反演结果更集中；且Red-Edge Added处理RF模型反演结果与观测值更接近1:1线，其精确度达到0.9186。另外，MLR、RF模型反演的蓄积量在较低水平（小于50m3·hm-2）的均高于观测值，而在较高水平（大于100m3·hm-2）的均低于观测值。

图2 无红边波段(a)和加入红边波段(b)后预测样本在多元线性回归(1)和随机森林(2)模型蓄积量的反演结果Fig.2 The forest stock volume retrieved results of the multiple linear regression model (1) and the random forest regression model(2) based on the predicting samples for the No Red-Edge treatment (a) and the Red-Edge Added treatment (b) respectively

2.3.4 精度分析

由表7可见，相对于No Red-Edge处理，在加入红边波段后，MLR模型反演结果与观测值拟合的决定系数R2表现出一定的提高（由0.5172增大到0.5487），但其均方根误差几乎没有发生变化（由26.4m3·hm-2到26.3m3·hm-2），表明MLR模型不具备检测GF6-WFV的红边波段对西宁市针叶林蓄积量反演影响的能力。而对于RF模型，在加入红边波段之后，其决定系数R2则表现出了明显的增高（由0.6120增大到0.6719），且均方根误差降低了10.3%（由23.2m3·hm-2降至20.8m3·hm-2）。对表7中的数据进一步分析可知，与MLR模型相比，RF模型在No Red-Edge、Red-Edge Added处理的决定系数R2分别提高了18.3%、22.5%，均方根误差分别降低了12.1%、20.9%。表明RF模型可以更好地检测出红边波段对蓄积量反演影响，在去除模型对反演精度的影响后，相对于No Red-Edge处理，Red-Edge Added处理的反演结果与观测值拟合的决定系数R2提高了11.6%，均方根误差降低了9.1%。

表7 无红边波段和加入红边波段处理下不同模型的森林蓄积量反演精度结果对比Table 7 Comparison of the retrieved precision of the forest volume for different models under the No Red-Edge and the Red-Edge Added treatment

3 结论与讨论

3.1 讨论

（1）遥感影像的纹理特征增强了森林冠层与灌草的差别，因而在森林蓄积量的遥感反演研究中得到了广泛的应用[32-33]。有研究指出纹理特征是物体的空间结构特征的显示，与影像的光谱特性无关，因此可以任意选择一个波段[34]，王月婷等[4,35]的研究就采用了Landsat8的全色波段。但也有研究表明不同波段的纹理特征对森林蓄积量的影响不同，刘俊等[32]研究得到近红外波段与柞树蓄积量具有较强的相关性，曹霖等[18]也将不同波段的纹理指标作为不同的纹理特征变量。本研究No Red-Edge处理中选取了GF6-WFV前4个波段的纹理指标，分析处理后，筛选出的主成分信息集中在红波段与近红外波段，这与张沁雨等[24,32]的研究结论一致。同时本研究在Red-Edge Added处理中选取了GF6-WFV前6个波段的纹理指标，且在筛选出的主成分信息中捕捉到了红边波段的信息，进一步表明在森林蓄积量的遥感反演研究中，需要考虑不同波段的纹理特征。

（2）本研究采用逐步回归法，筛选出了No Red-Edge、Red-Edge Added两组处理的自变量。对于Red-Edge Added处理，红边1波段（B5）的地表反射率入选，这与Hu等[16]的研究结论一致。Red-Edge Added处理中，植被指数只有MTCI指数入选，而MTCI指数主要用于反映植被冠层的绿素含量，与NDVI相比，MTCI指数减少了大气、土壤背景的影响[36]，削弱反射率的“碗边效应”[37]，更适合遥感定量反演与植被生长的参数[38-39]。另外，本研究中的NDREI指数未入选，从计算公式来看，尽管MTCI与NDREI中的两个红边波段均参与计算，但MTCI涉及红波段，而NDREI只是两个红边波段的运算，进一步表明即使加入红边波段，红波段对蓄积量的贡献不可忽视，曹霖等[18]研究证实了这一点。

（3）本研究采用不同模型对有无红边波段处理的蓄积量进行反演，结果表明加入红边波段以后，针叶林蓄积量的反演精度得到了提高，均方根误差降低了9.1%，这与曹霖等[18]在2018年基于Sentinel-2对吉林省中东部的森林蓄积量的反演结果一致。与此同时，本研究发现蓄积量在较低水平（小于50m3·hm-2）的反演结果均高于观测值，而在较高水平（大于100m3·hm-2）的反演结果却低于观测值，这在曹霖等[18]的研究中同样有此“饱和”现象，曹霖等[18]解释这可能与植被指数的“饱和”现象有关。

（4）本研究引入红边波段后提高了针叶林蓄积量的反演精度，但与观测值相比，还存在着诸多不确定性及误差，主要表现在：①数据在时间上的匹配度：本研究忽略了蓄积量获取时间与影像数据获取时间的滞后性，尽管针叶树种在一个龄级内生长缓慢，但在初期（蓄积量较低水平）由于生长速率较快，可能会出现反演结果高于观测值，而在后期（蓄积量较高水平）生长速率降低，反演结果低于观测值的情况；②蓄积量的观测误差：本研究的蓄积量数据来源于西宁市2014年森林资源二类调查数据，尽管对蓄积量的原始数据进行了数据清洗及预处理，但也会存在因调查小班数目多、分布广、参与观测人员多等原因而导致的观测误差；③遥感影像的选择：本研究采用光学遥感对蓄积量进行反演，但光学遥感并不能穿透树冠，缺乏更多森林内部结构等信息，进而影响蓄积量的反演精度；④模型的选择：本研究只选取了多元线性模型与随机森林模型来反演西宁市针叶林的蓄积量，缺乏更多模型（如支持向量机、KNN模型、BP神经网络等）的对比印证。因此，在后续蓄积量的遥感反演研究中，需要引入多源数据包括光学、高光谱、雷达遥感以及LiDAR等，结合同期的蓄积量实测数据，兼顾反演模型的适用性，从森林蓄积量的形成机理出发，在宏观与微观尺度上对森林蓄积量的遥感反演作综合研究。本研究揭示了红边波段在针叶林蓄积量的遥感反演方面的作用，为森林蓄积量的遥感反演及红边波段的应用提供了更多的科学参考。