基于Matlab仿真的四旋翼自抗扰控制算法的研究
2022-05-20刘灵童王大海尹晓娇
刘灵童,王 旭,王大海,郑 凯,尹晓娇
(西安石油大学 电子工程学院,陕西 西安 710065)
1 数学模型的建立
为了使计算机更好地控制四旋翼的运动,需要建立四旋翼的动力学模型。为了建立出的数学模型不失一般性,对飞行器做出如下假设。
(1)四旋翼飞行器为均匀对称的刚体;
(2)惯性坐标系原点E与四旋翼飞行器的几何中心和质量中心都处于同一位置;
(3)飞行器有且只受螺旋桨产生的拉力和重力的影响,即质量与转动惯量不变;
(4)飞行器所受的各个方向的拉力与螺旋桨转速的平方成正比例。
首先建立两个基本坐标系,分别为惯性坐标系和飞行器坐标系,如图1所示。这两个坐标系之间的转化关系如下。
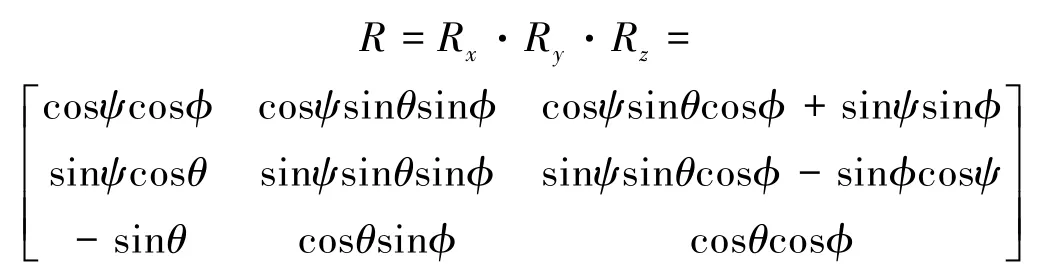
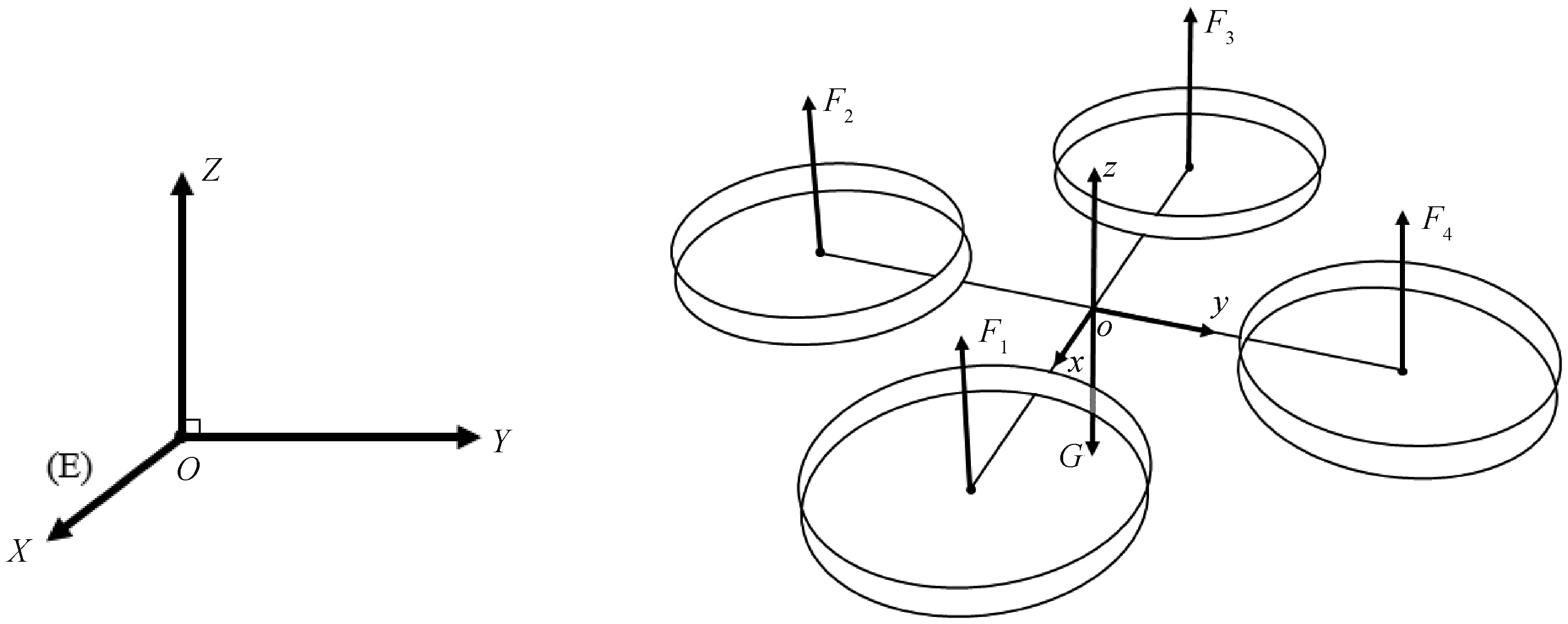
图1 飞行器坐标系与四旋翼结构模型
为了方便后续运算,相关定义如下:
偏航角ψ:x在OXY平面内的投影与x轴的夹角;俯仰角θ:z在OXY平面内的投影与z轴的夹角;翻滚角φ:y在OXY平面内的投影与y轴的夹角;
Fx,Fy,Fx分别为飞行器所受总拉力F在B(oxyz)中3个坐标轴上的分量;p、q、r为角速度ω在B(oxyz)中3个坐标轴上的分量。由于牛顿第二定律和力学方程可表示为:

根据假设四旋翼均匀对称,其惯性矩阵可定义为对角阵I。对飞行器动量矩计算,可得到飞行器力矩之和M在飞行器坐标系3个轴向分量Mx,My,Mz的角运动方程:
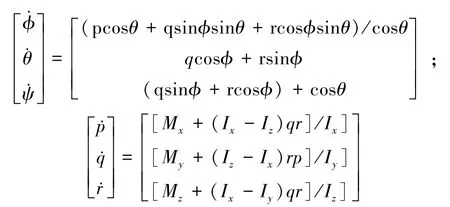
为了方便后续算法控制,可定义U1为垂直速度控制量,U2为翻滚输入控制量,U3为俯仰控制量,U4为偏航控制量,这样可以通过这四个独立控制通道来控制整机的运动。根据图1的姿态关系,可得出:
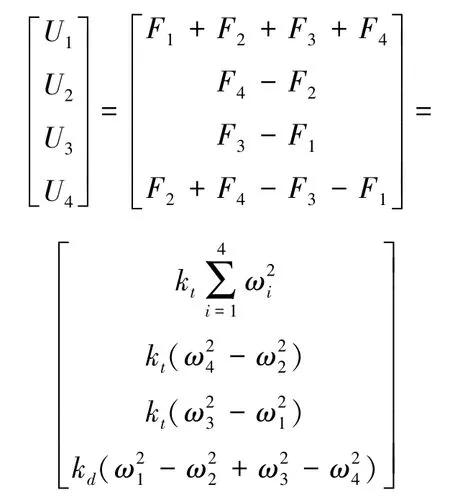
整理上述公式,可得到四旋翼的数学模型如下所示。
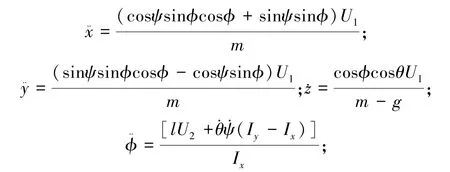

2 自抗扰飞控算法
上文在建立四旋翼数学模型时引入了4个控制量U,这样可以将复杂的非线性耦合模型转化为4个较为独立的控制通路,这样,整个模型的运动过程就可以分解为线运动和角运动。为了简化控制系统,假设飞行器的姿态角和加速度之间存在简单的积分关系,再根据相关资料对无人机的描述与测定,通过系统的传递函数,可总结出各个控制通道的传递函数[2],如表1所示(注:表1传递函数仅针对一款四旋翼飞行器的控制通道)。
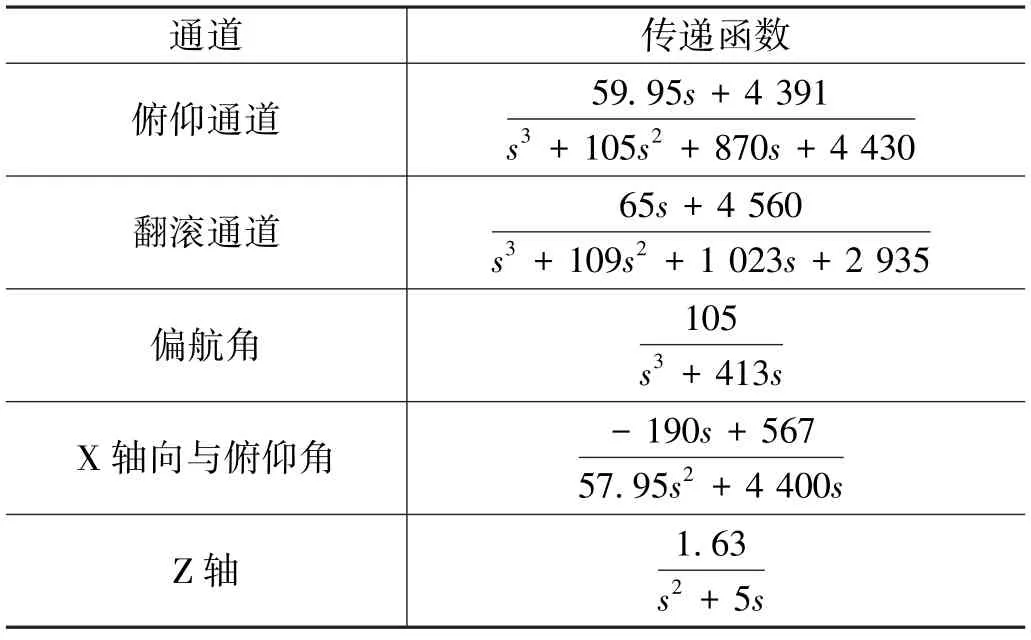
表1 各个通道的传递函数
在完成自抗扰控制之前,需要先对微分控制器进行一定的了解与设计。
2.1 微分跟踪控制器
在许多控制系统中,求输入信号的微分是控制器中必不可少的一个步骤,四旋翼控制系统也不例外。但是,在较多实际应用中,输入信号往往会伴随着噪声一同进入微分环节,利用差分法进行运算也会使得微分环节输出信号中的噪声不降反升,为了解决这一问题,人们设计了二阶微分器来尽可能地抵消噪声对于输出信号的影响。其传递函数如下:
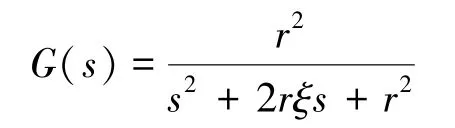
由传递函数可知,在低频段该环节的微分特性与纯微分环节的频率特性几乎一致,在高频阶段,其增益是随着频率的升高而下降的。噪声抑制的问题得到解决后,将我们合适的动态设计加入该环节,就得到了微分跟踪控制器。在Matlab中,以Z轴通道为控制对象,将随机的高频噪声叠加在正弦信号中作为该控制器的输入信号,观察输出信号与预期位置的对比,观察其动态性能。如图2所示,尽管输入信号存在较多高频尖刺等噪声,微分控制器依然可以在过滤掉大部分毛刺的同时,保证一个较好的跟随性能。为了利用其良好的性质,部分自抗扰控制算法也会包含微分跟踪环节。
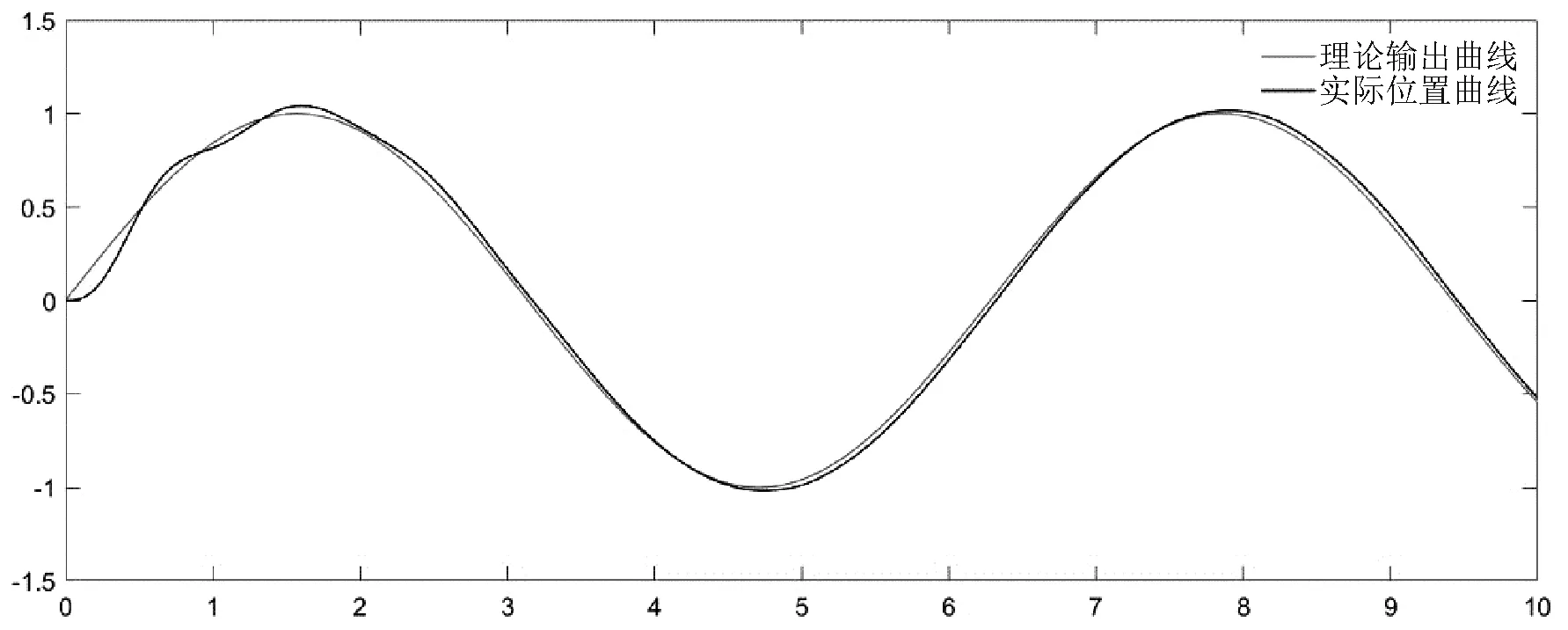
图2 理想位置与系统实际位置对比
2.2 自抗扰控制
为了进一步改善PID控制器在强干扰环境以及不确定因素中的控制能力,由韩教授首次提出了自抗扰控制(Active Disturbance Rejection Control,ADRC)的概念,这种控制器的核心思想在与利用一个环节来实时地估计被控对象的外部干扰和内部震荡,然后再用其他环节实施补偿,从而使得自抗扰控制系统具有较好的抵抗扰动的能力[3]。线性自抗扰控制基本结构,如图3所示。
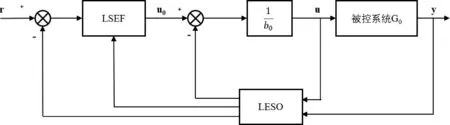
图3 线性自抗扰系统结构
其中G0表示需要被控制的对象,b0为整个系统的控制增益,它是由整个被控系统来确定的,需要在后期整定。LSEF为线性状态误差反馈,在不同场合中,这个环节可以用微分跟踪器来代替。LESO为线性扩张状态观测器,其形式为:
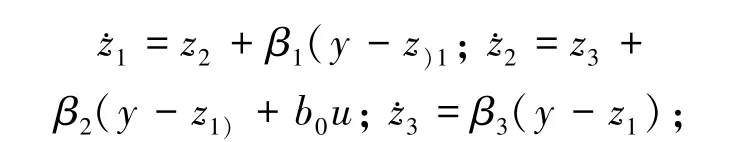
其中z1,z2,z3是LESO的3个输出量,β1,β2,β3都是需要在之后确定的观测参数。
假设被控对象可以被估计为一个二阶模型:
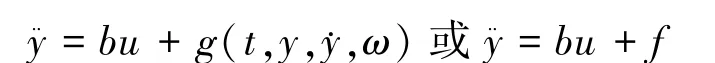
g可以看成是内部动态和外部扰动(ω)的综合特性,当ESO被正确整定时,z1,z2,z3将分别对y,y·,f进行跟踪,那么控制系统就会转化成两个积分串联环节,即
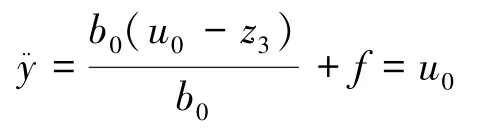
那么,对于常规的PID控制来说,LSEF就可表示为PD控制:
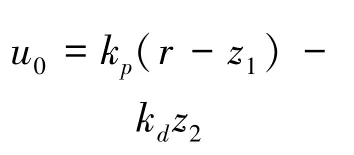
这样,就出现了b0,kp,kd,β1,β2,β3一共6个参数需要整定。当然,根据系统的传递函数,可以根据以下方法完成所有参数整定[4]:
(1)根据已知被控对象要求的调节时间t∗s,令,ωo=kωc,使kp=ω2c,kd=2ωc,β1=3ωo,β2=,β3=kβ2;在一般情况下k取4。
(2)逐渐增大b0的值,到动态响应性能指标满足系统要求。
本次将使用Simulink仿真环境以x轴和俯仰通道作为被控对象进行设计。因为ESO的输入中需要y·,所以,可以将一个积分环节独立出该通道的传递函数中,并且重新设计增益,方便后期的仿真系统的搭建。根据计算,修改完成后的被控对象的仿真搭建如图4所示。
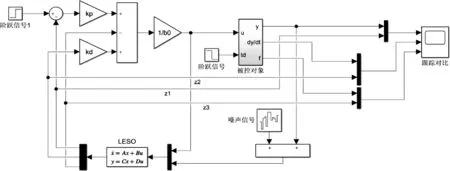
图4 调整后被控对象的仿真搭建
其中,u和td是被控对象的两个输入,y为系统输出,dy/dt也就是输出的导数,f为被控对象的总扰动。之后,根据ADRC的控制基本框图完成仿真模型的搭建,如图5所示。
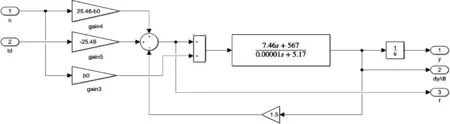
图5 线性自抗扰仿真系统搭建
其中,z1,z2,z3分别为LESO的3个输出,与系统输出y,,f进行对比显示。为了模拟其在实际控制中可能遇到的高频噪声或者是内部信号突变干扰,在LESO前加入了噪声模块,在控制对象的td输入口接入了负阶跃信号,将在第3s仿真时间输出值由0跳变为1。按照上文步骤进行参数整定,整定结果为:b0=180,ωc=20,ωo=80;运行仿真程序后,其结果如下所示:
从图6中可以看出,ESO的观测跟踪效果显著,即使在反馈回路中加入了相关干扰控制系统也可以在0.5 s内使系统输出为给定值并且达到稳态。为了探明系统自身变化对控制结果的影响,将被控对象的增益做±10%步长4%的变化,以调节时间为采样点,进行统计,其结果如表2所示。
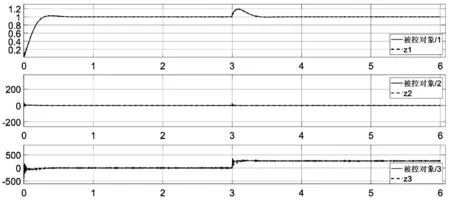
图6 线性自抗扰系统多干扰响应曲线

表2 变增益动态性能对比
由此数据可得,自抗扰控制对被控对象的精确数学模型需求并不强,也就说明,当四旋翼飞行器部分参数改变时,此种算法依旧可以保持一个较为稳定的控制结果。这种控制能力对于四旋翼飞行器至关重要。
3 结语
本文以四旋翼飞行器为研究对象,建立了其数学模型,根据该模型,使用Matlab进行自抗扰控制的仿真。从仿真结果来看,自抗扰控制系统对高频信号干扰与外部参数补偿两个方面的控制效果都较好,总结出了其动态性能等相关规律,为相关四旋翼控制算法的实现与发展提供了结论支撑。
