贵州省高新技术企业自主创新能力测算与评价

2022-05-19李凤培

云南科技管理 2022年2期

关键词：原始数据信息熵高新技术

张鑫，李凤培，张平

（1.贵州师范大学材料与建筑工程学院；2.贵州师范大学，贵州贵阳 550025）

0 引言

到2020年，贵州省高新技术企业数量已达1 000家。尽管近几年取得了一些成绩，但是也应该清醒意识到差距与不足，贵州省在经济发展方面还远远落后于其他地区，在高新技术企业发展方面的不足更是显而易见，从政策、人才等资源来看，都有很大发展空间。

1 评价指标体系的建立

1.1 构建原则

整体性原则。企业自主创新能力不是单一因素作用的结果，它受企业内部和外部多种因素共同影响，各个因素相互联系，相互支撑，在评价企业自主创新能力时，应将各个因素看为整体，才能准确全面。

科学性原则。科学性是企业自主创新能力评价各个环节工作的基础。在基于科学性原则上，才能挖掘企业自主创新能力的本质和发展规律，因此科学选择指标，才能降低误差，使得测算更加接近企业真实情况。

对比性原则。文章所选取的是贵州省各个行业，以及不同行业不同年份的指标进行比较，形成对比，从中发现各个企业的不足与差异，对症下药。

动态性原则。在评价企业自主创新能力时，不仅要对企业过去以及现状进行分析，还要对其发展趋势进行预测，所以在选择指标时，应该将潜在因素纳入考虑。

可实施性原则。指标的选择与建立不仅要考虑其能否满足本研究的需求，更要保证数据完备、来源真实可靠。

1.2 评价指标体系的设计与构成

在总结以往研究经验的基础上，依据构建原则与企业发展规律与企业各职能部门的职能，参考国家统计局发布的《中国企业自主创新能力分析报告》，从企业潜在创新资源、创新活动投入、创新成果、创新环境4个层面建立贵州省高新技术企业自主创新能力评价指标体系（表1）。

表1 贵州省高新技术企业自主创新评价体系

2 高新技术企业自主创新能力测算

2.1 样本的选择

我国目前并没有对高新技术行业进行明确的界定，但会根据技术密集与复杂水平来衡量行业是否属于高新技术行业范围。2007年国家统计局发布了有关高新技术行业分类的文件《高新技术产业统计分类目录的通知》，将航天类相关的制造业、医药制造业、计算机、电子及通信设备制造业、仪表仪器制造业、信息传输、软件和信息技术服务行业与科学研究与技术服务行业以及其他纳入高新技术行业统计范围。

选取具有代表性的六大高新技术行业作为研究对象，分别是医药制造业、计算机、通信设备和其他电子设备制造业、信息传输、软件和信息技术服务行业、科学研究与技术服务业、仪器仪表制造业与铁路、船舶、航空航天和其他运输设备制造业，并选用近几年的数据进行研究。

2.2 数据获取与处理

文章搜集到的数据均来自贵州省科技局所编著的《高新技术企业统计年鉴》中六大行业的相关数据，根据之前建立的高新技术企业自主创新能力评价体系搜集相应的指标数据，并整理于表中。为了方便数据的统计与整理，用字母B1、B2、B3、B4、B5、B6分别代表医药制造业、铁路、船舶、航空航天和其他运输设备制造业、计算机、通信设备和其他电子设备制造业、仪器仪表制造业、信息传输、软件和信息技术服务行业、科学研究与技术服务业（见表2）。

表2 2019年贵州省六大行业原始数据

2.3 测算方法

2.3.1 熵值法

从目前已有的研究得知,很大一部分学者在对高新技术企业自主创新能力评价时采用的都是层次分析法、专家调查法等诸如此类的主观赋权法，这些主观赋权的方法对研究者的科研素质与专业知识要求极高，倘若研究者不具备过硬的素质去进行判断赋权，会引起偏差，进而影响评价结果的科学性、合理性。而熵值法正好避免了这些问题，因为熵值法属于客观赋权法，通过客观的数据计算对指标进行赋权，不存在因为主观因素造成的偏差。

1）熵值法的基本原理

熵在信息论中的意义是度量不确定性，信息量与不确定性反向变化，熵值与不确定性成正向变化。我们可以根据熵值的特点对指标进行计算，通过熵值判断指标离散程度，进而可以看出该指标对于整体评价的影响力。所以，本文通过对信息熵的计算，计算各个指标相应的权重，为企业自主创新能力的评价提供科学的根据。

2）熵值法计算过程

①指标的标准化处理

指标的标准化处理就是将异质指标同质化。文章所选择的各个维度下的指标计量单位并不完全相同，因此，要将所有的指标同质化才能计算，这个过程就是指标绝对值的转化过程。另外，对于指标的分类，根据对整体评价的影响不同，将指标分为正向的指标和负向的指标两大类，对于不同类型的指标，其标准化处理的过程也不同，详细计算方法如下：

(文中i表示各个行业，j表示指标，Xij表示各个数据的原始值，max Xij是第i个行业的第j个指标的最大值，而min Xij是第i个行业的第j个指标的最小值)

正向指标的计算公式为：

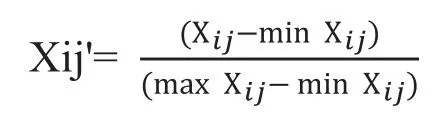
负向指标的计算公式为：

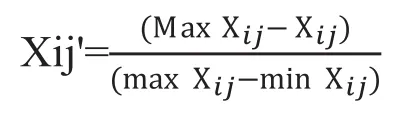
②归一化指标

在计算熵值，也就信息熵之前，先计算出第i个行业的第j个指标值的比重，具体计算公式如下：

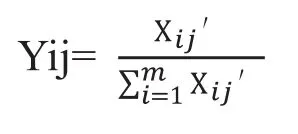
③计算指标的信息熵

计算信息熵是整个计算过程中较为关键的步骤，因为要根据最后计算出的信息熵来判断该指标对于整体评价的影响大小，当信息熵值越小，该指标的离散程度越高，对于整体评价的影响力也就越大，指标信息熵具体如下计算：

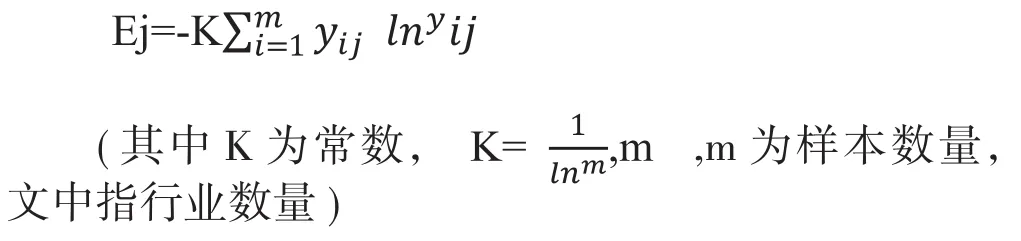
④计算每个指标的差异系数

对某个指标来说，指标值差异越大，对整体评价的影响力就越大，而且其差异越大，熵值越小。

Gj=1-ej

⑤计算指标权重

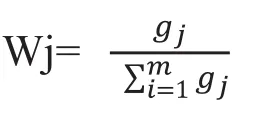
2.3.2 灰色关联度分析

采用熵值法计算出每一个指标相应的权重之后，结合灰色关联度模型计算出每个企业自主创新能力的综合分数，使得最后的计算结果更加准确可信。企业的自主创新能力越强，所得到的灰色关联度值越大，企业的自主创新能力越弱，则得到的灰色关联度值越小。

1）明确数据序列

确定原始数据序列为{Xi(1),Xi(2),Xi(3),Xi(k)……Xi(n)},其中，i=1,2,……m，k=1,2……n，m代表行业数量，n代表指标个数。

2）原始数据无量纲化

原始数据单位并不统一，将原始数据进行无量纲化的方法是均值法。具体计算过程如下公式：

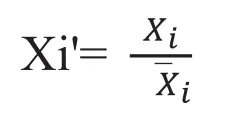
3）确定参考序列

原始数据无量纲化得到新数据之后，从每个指标中选择最优值，得到参考数据序列。将参考数据序列设为{X0'(1),X0' (2),……X0' (n)}

4）计算差值序列

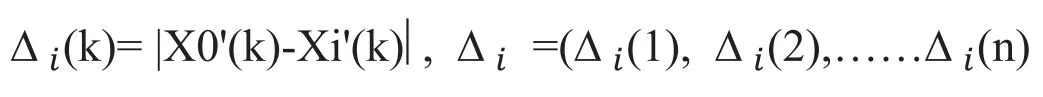
5）计算灰色关联度系数

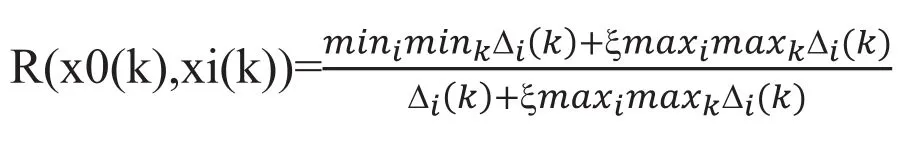
其中ξ为Δmax的系数，灰色关联度值大小在一定程度上取决于ξ的大小，本文采用最优值计算方法，避免了主观性的干扰，得到了ξ的最优值为0.5。

6）计算灰色关联度值

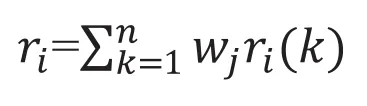
(Wj为文中已经计算出的每个指标的权重)

2.4 测算结果

依据熵值法计算出各年份不同维度的熵值与权重，再与灰色关联度分析相结合，得出各个行业不同年份的自主创新能力综合得分。根据各个指标每年相应的数据计算出权重，权重根据每年数据与情况的不同而发生变化，计算结果更加准确（见表3）。

表3 2019年各指标熵值与权重

2.4.1 自主创新能力综合评分计算

因为各个原始数据的单位不同，所以对原始数据进行无量纲化，得到数据的最优值，再求出差序列，根据差序列的最大值与最小值进一步得到各个数据的灰色关联系数，最后依据熵值法求出的权重的到各个维度创新能力的得分（见表4，图1、图2）。

表4 2019年贵州省高新技术行业创新能力综合得分

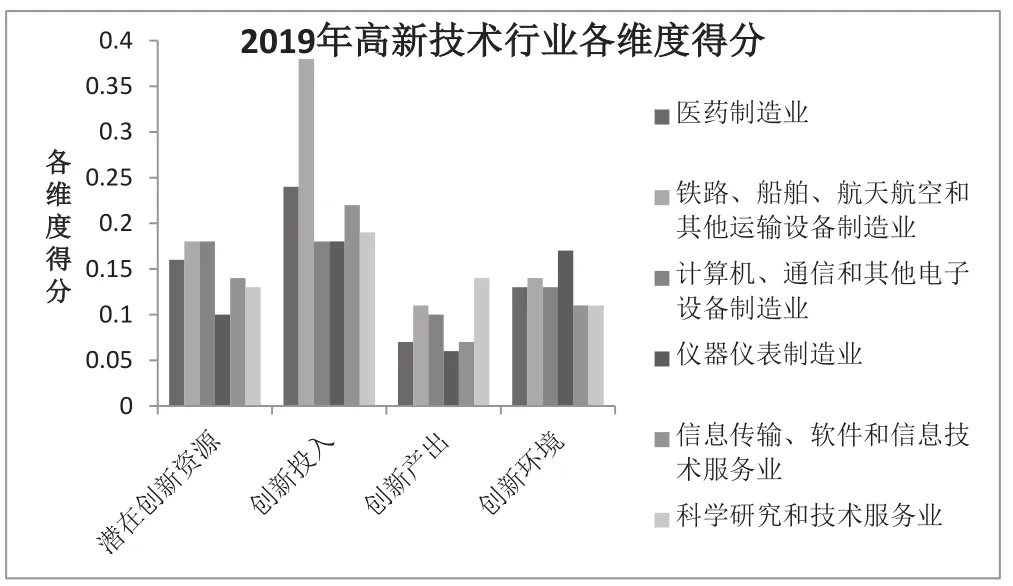
图1 2019年高新技术行业各维度得分

图2 2019年高新技术行业综合得分变化

3 高新技术企业自主创新能力测算结果分析

贵州省高新技术企业自主创新能力极其不均衡，各个行业差距较大。其中差距最为明显的是潜在创新资源，医药制造业与航空航天、船舶及其他运输设备制造业，这两大行业工业总产值领先许多，实力较强，为其自主创新发展奠定了基础，与其他行业明显拉开了差距，占据较大优势。另外，企业之间获得的高新技术企业所得税减免与企业投入的项目资金差距也带来了不均衡的创新发展。造成这种现象的原因有政府政策的倾斜、企业对自主创新的重视以及企业自身实力较强，所以有充足的资金投入到研究与开发中。

企业之间科研人员数量相差较大，也是导致发展不均衡的原因。可能是企业对于工作人员的科技素养与学历不够重视，企业的人才引进制度不够完善，所以缺乏创新核心力量。