延安新区黄土压缩特性试验研究

王 博， 黄雪峰,2,3， 邱明明， 王 寒

(1.兰州理工大学 土木工程学院， 甘肃 兰州 730050； 2.重庆交通大学 河海学院， 重庆 400074；3.陆军勤务学院 军事设施工程系， 重庆 401311； 4.延安大学 建筑工程学院， 陕西 延安 716000)

1 研究背景

天然黄土低湿度、低密度的大孔隙空骨架体系结构特点造成原状黄土特殊的结构性[1]。近年来，我国西部黄土山区特殊的地形地貌制约着城市的发展，因而兰州、延安等城市在黄土塬区开展了大规模的高填方工程[2-4]。在高填方工程中主要以黄土作为填筑材料，由于填土的压实度和含水率的差异，导致土颗粒的空间排列、次生联结和吸力胶结均有所不同，从而造成沟壑区高填方黄土复杂的压缩变形。因此，原状结构性黄土与填方结构性黄土在荷载和水耦合作用下的压缩变形规律成为高填方工程需要研究的关键性问题。

国内学者对黄土的高填方工程与结构性力学特性已开展诸多理论与试验研究，谢定义等[5]提出了释放结构势思想构造出黄土结构性的定量化参数，并验证了结构性参数的合理性；陈存礼等[6]通过揭示制样含水率与试验含水率引起压实黄土侧限压缩变形的特性规律，提出压缩指数和结构屈服压力与初始结构性参数有较好的归一化非线性关系；蒋明镜等[7]提出了非饱和结构性黄土三维胶结接触模型，并分析了其宏、微观力学机理；王丽琴等[8]分别给出原状Q3、Q2黄土构度指标与屈服压力的线性关系，表征出黄土沉积年代、基本物理参数与构度指标的函数模型；邵生俊等[9]将构度指标引入到湿陷性黄土变形与评价中，结合现场浸水试验与室内试验验证了其评价方法的合理性；陶虎等[10]将构度指标引入弦线模量表，采用三层法计算结构性黄土的沉降变形，提出了地基沉降变形的新方法；褚峰等[11]结合损伤力学思想构建了原状黄土结构变形损伤比的具体表达式，推导出一维湿压条件下的结构演化模型；葛苗苗等[12]对高填方压实黄土开展了固结蠕变试验，提出了黄土时效变形模型并能较好地预测高填方工程后期的沉降规律；张龙等[13]探究了延安市高填方填土的渗水与持水特性，揭示出填土渗透系数与饱和度二者的线性关系；张沛然等[3]通过研究吸力与压实度对非饱和压实填土压缩变形特性的影响，构建了填方区土体工后沉降变形修正计算模型；郅彬等[14]对延安地区黄土的次固结特性及压缩变形机制进行了研究，建立了次固结系数时间效应的关系模型。根据已有研究成果发现，黄土在沉积年代、密度以及增减湿、吸力等因素的影响下，造成其结构性、土体强度、压缩变形和地基沉降变形的差异性与复杂性。而在黄土塬区高填方工程中，关于填筑体的压实度和土体增减湿引起黄土的结构性变化规律，以及构建重塑黄土结构性参数与压缩指标函数模型的问题在现有研究文献中少有报道。

本文以延安新区某场地黄土为研究对象，通过开展原状黄土和重塑黄土的侧限高压固结试验，构建黄土在不同条件下(压实度K、含水率w)的结构性参数，揭示压缩指标与结构性的内在定量规律，并建立Q3原状黄土和重塑黄土压缩指标与结构性参数之间的关系模型，修正了黄土湿载压缩模型，结合试验结果对模型进行了验证。研究成果可为黄土沟壑区高填方工程的实践与理论研究提供参考。

2 试验材料与方案设计

2.1 试验土样

试验用土取自延安新区某黄土场地工点，土质年代为Q3，呈浅黄色，天然含水率为13.8%～15.3%，初始黄土密度为1.43 g/cm3。根据土工试验标准得出黄土土样的物理参数指标如表1所示。基于标准夯击试验测得黄土的最优含水率wop=15.3%，最大干密度为1.75 g/cm3。原状黄土制备需检验其结构是否受到扰动，对未扰动的黄土采用滴定法或风干法进行目标含水率试验土样的制备，重塑样的制备需进行风干脱湿、过筛(采用2 mm的土筛)、增湿(每次增湿不超过5%)配制试验土样，然后密封静置养护至少72 h，使土样中水分保持均匀。土样横断面面积为100 cm2，高度为20 mm。

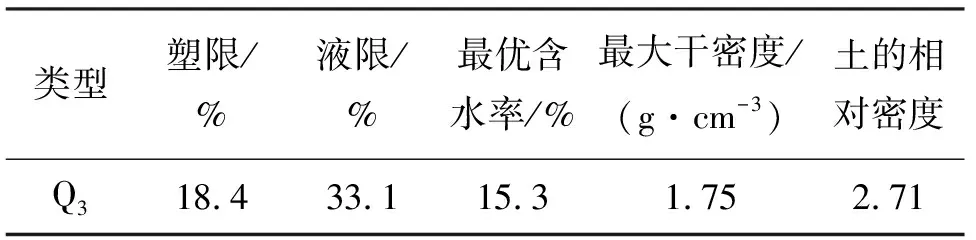
表1 试验黄土土样的物理参数指标

2.2 试验方案

本次压缩试验采用WG型三联高压固结仪，加荷等级依次为50、100、200、300、400、500、600、800、1 000、1 200、1 400 kPa，加荷稳定标准为变形小于0.01 mm/h。

为揭示原状黄土与重塑黄土在不同条件下(即不同压实度和含水率)的压缩变形规律，定量探究结构性参数与基本物理参数的关系，本次试验制备了压实度K分别为70% (干密度1.23 g/cm3)、80% (干密度1.40 g/cm3)、85% (干密度1.49 g/cm3)、90% (干密度1.58 g/cm3)的黄土试样，对每一种压实度试样又设置了6种不同的含水率，含水率分别为10.3%、13.3%、15.3%、17.3%、20.3%及饱和状态 (为表示方便记为组A)，对上述不同干密度与含水率组合的黄土试样进行侧限高压固结试验。每种组合的土样不少于3个，对于压缩曲线差异性较大的土样则废弃重做，具体的试验方案见表2。

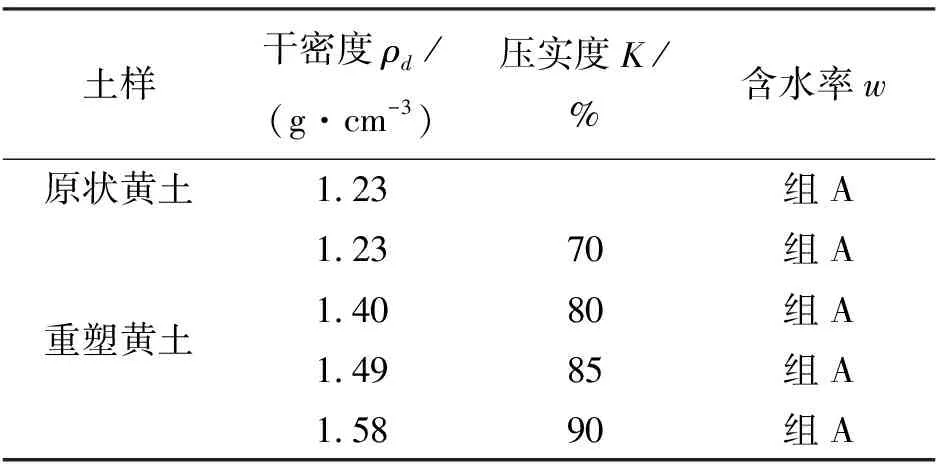
表2 侧限高压固结试验方案

3 结果与分析

3.1 物理性质对黄土压缩曲线的影响

在同一干密度下，不同含水率的原状和重塑黄土的孔隙比e-压力荷载p关系曲线见图1。由图1(a)可知，随着压力荷载的增大，原状黄土的架空颗粒骨架结构受到破坏，土颗粒逐步被压实，孔隙比随着压力的增大而减小。e-p曲线随着压缩荷载不断增大，曲线的斜率会逐渐增大直至斜率保持不变，曲线呈现平缓下降与急速陡降两个阶段，平缓阶段为结构可稳性的自身调整，平稳阶段越长，说明原状黄土骨架承受外力与水的作用越强。当荷载增大至土骨架承受荷载的极限状态时，土骨架迅速被破坏，致使土体进入快速的压缩变形阶段，此时破坏所对应的压力即为结构屈服压力psc[15]。当含水率逐渐增大时，平稳阶段缩短，结构屈服压力减小，曲线在陡降段斜率逐步增大，这是由于土体水分溶解了黄土颗粒间的可溶性矿物和盐晶等胶结物，削弱了颗粒间的凝聚力，造成土体可变性增大，反映出黄土压缩变形会随着含水率的增大而增大。对重塑黄土进行相同干密度的扰动试验(图1(b))，结果表明，e-p压缩曲线随含水率的增大而下移，曲线急速陡降段的斜率比原状黄土大，表明黄土的结构性基本丧失，黄土颗粒受荷载作用迅速滑移坍塌并重新排列，且平缓阶段较原状黄土明显缩短。

以K=80%和K=90%重塑黄土土样为例，不同含水率条件下重塑黄土的孔隙比e-压力荷载p关系曲线见图2。由图2可知，在同一荷载下，随着含水率的增大，土样的孔隙比减小。这是由于在压力荷载作用下，土体的抗变形能力主要由颗粒间的摩擦力与凝聚力提供，而随着含水率的增大，土颗粒间的凝聚力与摩擦力逐渐减小，因而土体抵抗压缩变形的能力减弱。将不同初始含水率的土样增湿至饱和后再进行侧限压力固结试验，比较图2(a)与2(b)中两组增湿至饱和土样的e-p曲线可见，随着压实度的提高，不同初始含水率的e-p曲线分布间距减小且趋于归一化，表明随着压实度的增大，重塑黄土初始含水率对饱和土样骨架结构的影响减小，对黄土的压缩变形影响也减小。

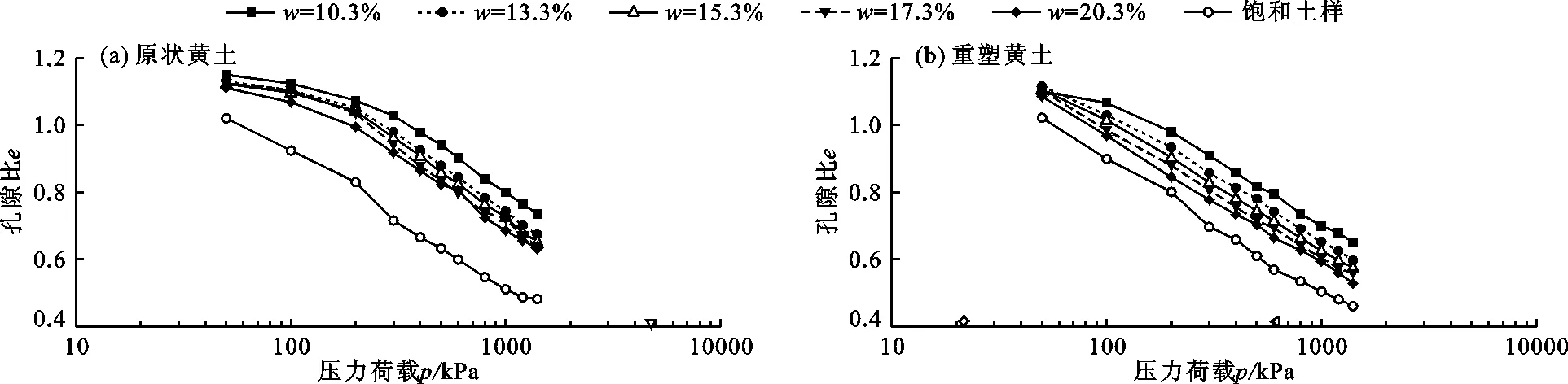
图1 不同含水率条件下原状黄土及重塑黄土的e-p关系曲线

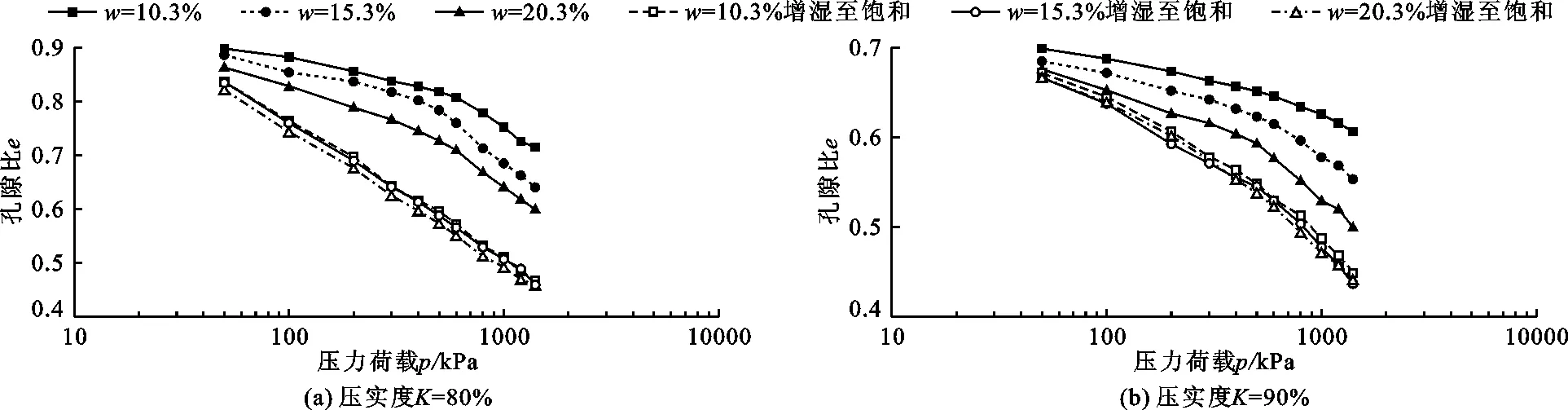
图2 压实度K=80%、90%时不同含水率重塑黄土的e-p关系曲线

当含水率w=15.3%时，原状黄土及不同压实度重塑黄土的孔隙比e-压力荷载p关系曲线见图3。由图3可知，e-p关系曲线的平缓段随着压实度的提高而增长，土样的压缩屈服压力逐渐增大，表明原状黄土颗粒间的搭接点接触与面胶结比压实重塑黄土更易受到压力破坏，而重塑黄土颗粒内部的移动与滑移也随着压实度的增大而受阻，即颗粒间的摩擦力增大；在相同压力荷载作用下，随着压实度的增大，黄土骨架破坏时所对应的压力也增大，即结构的屈服压力psc增大，土样的压缩变形逐渐减小。

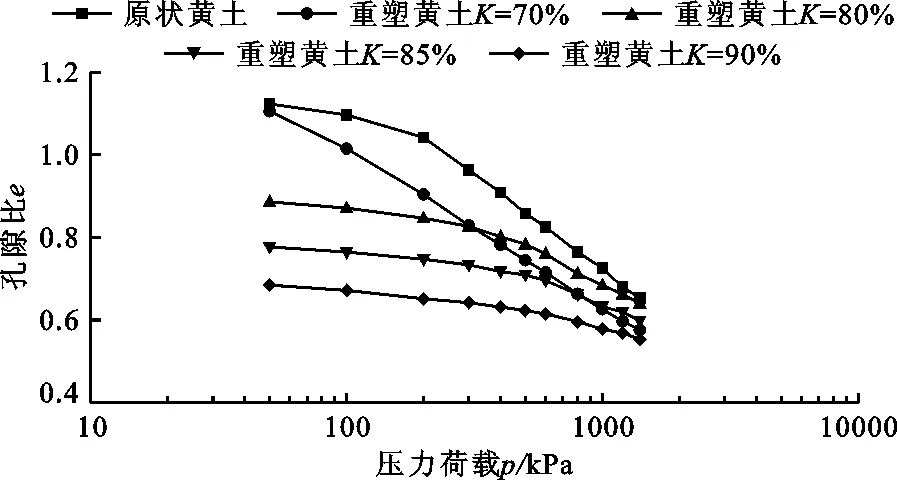
图3 原状黄土及不同压实度重塑黄土的e-p关系曲线(w=15.3%)

3.2 物理性质对黄土压缩指标的影响

黄土变形最大的特性就是变异性很大[16]，在工程实践中通常采用压缩指标(结构屈服压力psc、压缩指数λ)来反映黄土的压缩变形。本文采用Lebert/Horn法[17]计算黄土的结构屈服压力，将上述各e-p曲线转化为两段e-p关系直线，以两段直线交点对应的压力作为黄土结构的屈服压力，拟合出原状黄土及不同压实度重塑黄土的结构屈服压力psc-含水率w关系曲线，拟合结果见图4。

由图4可以看出，当压实度相同时，结构屈服压力随含水率的增大呈非线性减小趋势，表明土样的含水率削弱了颗粒间联结键的化学作用，在荷载作用下加速了颗粒骨架的结构损伤，使骨架结构发生屈服破坏时相应的荷载减小；当含水率相同时，结构屈服压力随压实度的增大而逐渐提高，说明随着土样压实度的增大，重塑黄土初始结构的抗压缩变形性能也明显增强，结构屈服压力随之增大；重塑黄土的压实度越大，其结构屈服压力随含水率增大而减小的趋势越明显，表明初始含水率相同的重塑黄土随着土样孔隙比的减小，其抵抗压缩变形的能力明显增强，但随着含水率的增大，骨架结构被明显削弱，结构屈服压力也随之快速减小。

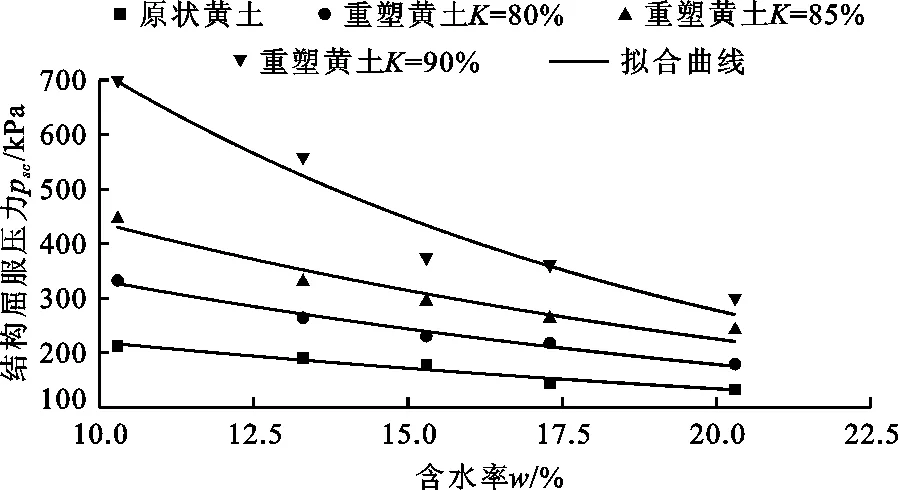
图4 原状黄土及不同压实度重塑黄土的Psc-w关系曲线

在高填方工程中，填筑体的沉降变形是工后进行施工建造需考虑的首要因素[18]，而黄土的压缩指数λ的大小反映出土体可变性的强弱，λ的取值为压力荷载大于结构屈服压力时e-p线段的斜率，据此绘制出原状黄土及不同压实度重塑黄土的压缩指数λ-含水率w关系曲线，如图5所示。

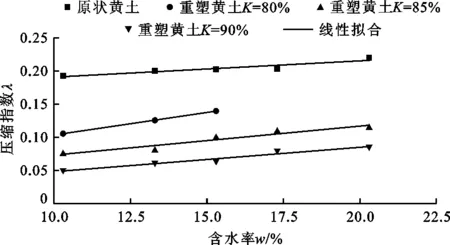
图5 原状黄土及不同压实度重塑黄土的λ-w关系曲线

由图5可见，当压实度相同时，在压力荷载作用下，含水率越大则压缩指数越大，即压缩变化量越大，与罗爱忠等[19]研究得出的λ随w变化呈正相关的结论一致，与图4中的psc-w曲线呈对应关系。分析认为，当压力荷载大于结构屈服压力时，土的骨架结构被破坏，土体进入塑性压缩阶段，其抵抗变形主要以颗粒间的摩擦力为主，而随着含水率的增大，颗粒间的摩擦力减小，导致变形增大，即压缩指数增大。图5还表明，含水率与压缩指数呈线性关系，且压缩指数逐渐向饱和土样的压缩指标靠近；随着压实度的增大，土样抵抗外力压缩的能力加强，土体变形减小，即压缩指数减小。

依据谢定义等[5]对原状黄土释放结构势的思想方法，建立原状黄土的结构性参数mε，对于不同压实度的重塑黄土，可依据陈存礼等[6]计算压实土的方法来计算其结构性参数，由于重塑土的初始土样骨架结构被破坏，土颗粒已重新排列、胶结构成了新的骨架结构，获取其结构性参数的方法是：对相同初始干密度和含水率的土样增湿至饱和，在侧限压力荷载p的作用下，相同应变条件下特定含水率土样的荷载应力与相应饱和土样的荷载应力的比值即为重塑黄土的结构性参数mε，对于饱和重塑黄土，其结构性参数mε=1。原状黄土和重塑黄土的结构性参数表达式分别为公式(1)和(2)。

(1)

(2)

式中：mε为黄土的结构性参数;σ0、σs、σr和σrs分别为同一应变下原状黄土、饱和黄土、重塑黄土和重塑饱和黄土的荷载应力，kPa。

选取在荷载作用下黄土最大的结构性参数为初始结构性参数mε0，黄土的初始结构性参数mε0-含水率w关系曲线如图6所示。由图6可以看出，在干密度相同的情况下，初始结构性参数随着含水率的增大而减小，原状黄土的结构性参数曲线高于重塑黄土的结构性参数曲线；原状黄土mε0-w曲线的变化斜率明显大于重塑黄土，而重塑黄土结构性参数曲线随着压实度的增大而提高，表明黄土的增湿对其初始结构性存在明显的影响，颗粒之间的连接强度在水的作用下逐渐丧失，发育良好的骨架结构在荷载作用下联接破坏提前，土体的初始结构性迅速下降。天然沉积的原状黄土比重塑黄土的骨架结构发育稳定，其颗粒间的碳酸钙与胶结矿物形成了加固凝聚力，使原状黄土有较强的结构性，在土体的压密过程中提供了有效的抵抗力。对于重塑黄土而言，由于颗粒间的胶结物受到扰动，抵抗压缩变形主要是颗粒间的摩擦力，而初始孔隙比的大小影响着土样的压缩变形，因此，重塑黄土的结构性随着干密度的增大而逐渐加强。

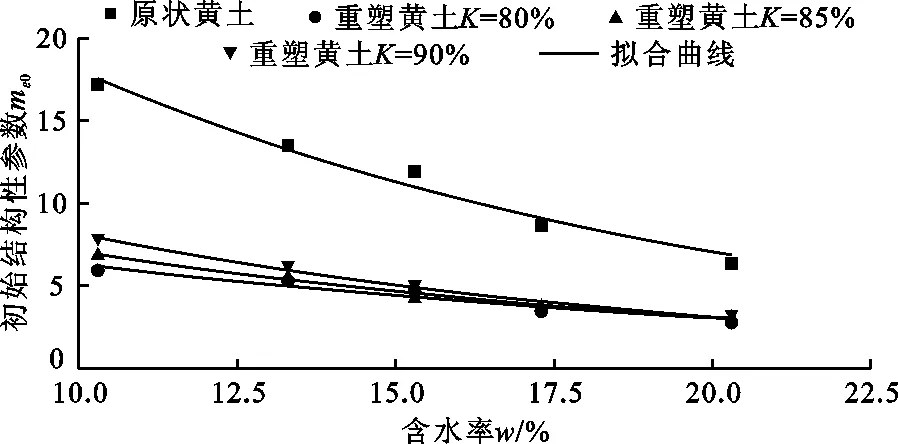
图6 原状黄土及不同压实度重塑黄土的mε0-w关系曲线

将图6中黄土在不同压实度的mε0与w数据进行非线性拟合，得出的拟合曲线与数据具有较高的吻合度，拟合函数表达式为：

mε0=aexp(-bw)

(3)

式中：mε0为初始结构性参数；w为土样的含水率；a、b均为试验参数。

3.3 初始结构性对黄土压缩指标的影响

黄土的压缩指标psc、λ与初始结构性参数mε0的关系曲线见图7。

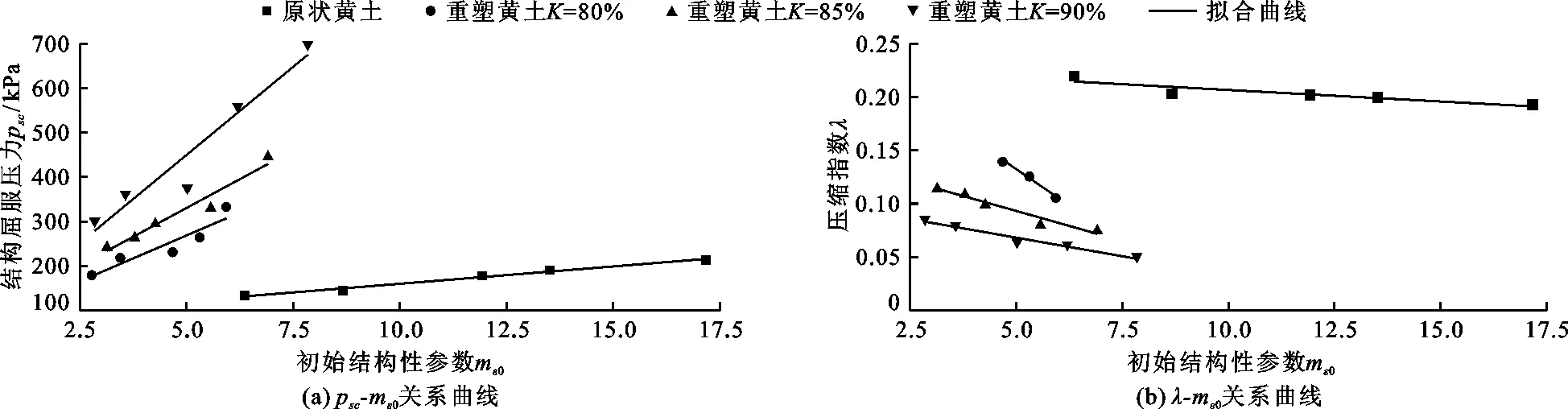
图7 原状黄土及不同压实度重塑黄土的psc-mε0、λ-mε0关系曲线

由图7(a)可知，当含水率w一定时，psc随着压实度K的增大而增大，mε0也愈来愈大，即重塑黄土颗粒骨架的密实性与结构屈服压力呈正相关，土样密实性越大，进入结构屈服阶段所需的压缩荷载越大，即黄土的结构性越强；当K一定时，psc随着w的增大而逐渐减小，mε0也愈来愈小，反映出颗粒骨架由于含水率的增大，在极小的荷载作用下，土颗粒引发错动区间越大，致使黄土的结构骨架遭到破坏，初始结构性参数减小，这与邓国华等[20]研究得出的黄土结构性指标mu与psc随w的增大而逐渐减小的结论一致。

由图7(b)可知，当土体K逐渐减小时，λ逐渐增大，mε0随着λ的增大而逐渐减小，λ与mε0呈负线性关系。当压缩荷载p大于psc时，土体的初始结构受到破坏，压缩变形进入塑性阶段时黄土颗粒的密实度影响着λ大小，密实度越大或含水率愈小，则在压缩过程中颗粒受到变形的阻力越大，即λ越小。

图7表明，psc-mε0及λ-mε0关系呈线性变化，故将其进行线性拟合，拟合函数表达式为：

psc=(amε0+b)pa

(4)

λ=-cmε0+d

(5)

式中：pa为标准大气压，kPa；a、b、c、d(a>0，c>0)均为拟合参数，其取值如表3所示。

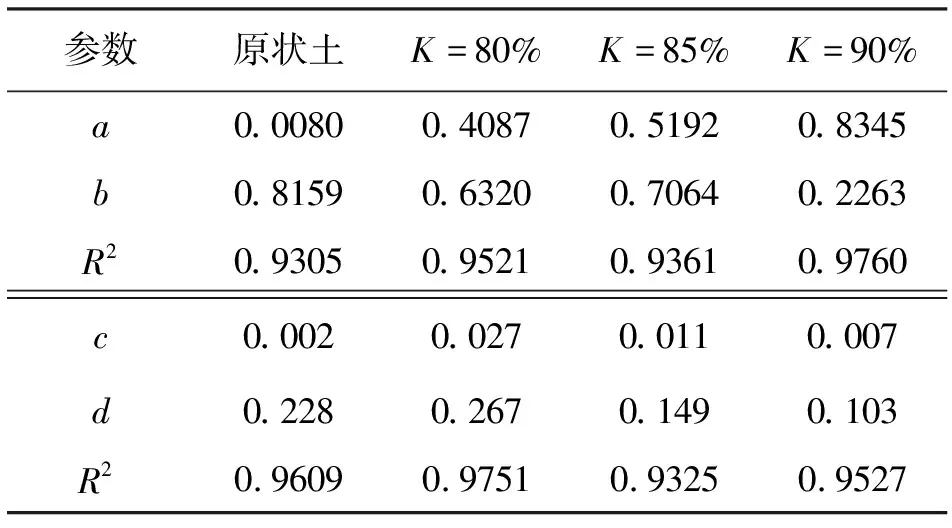
表3 黄土的psc-mε0及λ-mε0关系拟合参数取值

由表3可知，随着K值增大，拟合函数式(4)中的斜率参数a(K=80%时为0.407 8、K=85%时为0.519 2、K=90%时为0.834 5)逐渐增大，拟合函数式(5)中的斜率参数c(K=80%时为0.027、K=85%时为0.011、K=90%时为0.007)逐渐减小，表明土体压实度的增大以及湿度的变化对黄土的psc和mε0的影响逐渐增大，而对λ和mε0的影响逐渐减小。对于函数式(4) 、(5)表征的黄土结构屈服压力psc和压缩指数λ与初始结构性参数mε0的线性拟合关系，其拟合优度均大于0.93，拟合结果与试验数据的吻合度较高，基本能表示出psc和λ与mε0之间的线性关系。

4 黄土湿载压缩模型与验证

结构性黄土的e-p关系曲线可以按结构屈服压力分为弹性变形阶段与压缩(塑性)变形阶段，两段直线的斜率分别为弹性指数κ和压缩指数λ[21]。在同一压实度下，含水率的变化对κ值的大小影响较小[6]，结构性黄土的弹性指数κ值见表4。

表4 结构性黄土的弹性指数κ

结构性重塑黄土的弹性指数κ-干密度ρd关系曲线见图8，由图8可知，弹性指数随压实度(干密度)的增大而非线性减小。据此建立κ与ρd的函数关系式如下：

κ=aexp(-bρd)

(6)

式中：a=0.417 9；b=2.224 5。曲线的拟合优度达到0.991，拟合曲线与试验数据的吻合度较高。

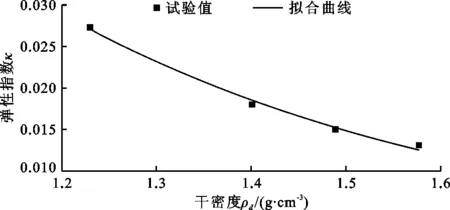
图8 结构性黄土的κ-ρd关系曲线

在侧限压缩状态下，黄土初始结构性的变化影响着psc、κ与λ的大小，因而将初始结构性参数mε0引入黄土的一维压缩变形的关系中。采用e-p关系曲线中的参数来计算孔隙比的变化量，建立压缩变形下的应力-应变关系模型。

当施加的压力荷载p小于psc时，黄土以弹性变形为主，结构性黄土的应力-应变关系如下：

(7)

当施加的压力荷载p大于psc时，黄土以压缩(塑性)变形为主，结构性黄土的应力-应变关系如下：

(8)

式中：ε为土的应变值；p为压力荷载，kPa；e0为初始孔隙比；p0为正常固结黄土应力[21-22]，kPa；psc(mε0)、λ(mε0)、κ(ρd)的取值可分别通过公式(4)、(5)、(6)确定。

在黄土高填方工程中采用分层总和法计算填方区总沉降变形，即首先计算出每一分层的沉降量Δhi·εi，再进行求和。因而填方区黄土总的沉降变形为：

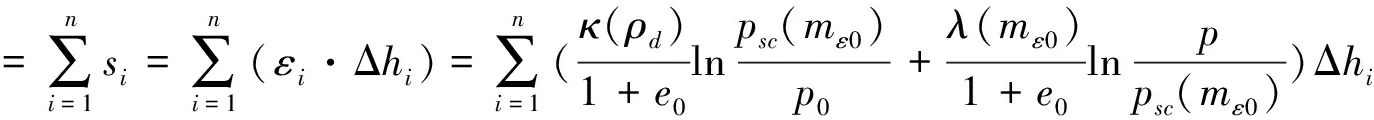
(9)

式中：S为总的沉降量，m；si为第i层土层的沉降量，m；εi第i层土层的应变值； Δhi为第i层土层的厚度，m。

将构建的应力-应变关系式(7)、(8)转化为黄土土样在侧限压缩状态下孔隙比的变化量，可对比修正陈存礼等[6]在压实黄土下的压缩变形模型，其表达式如下：

(10)

式中：e和e0分别为黄土压缩变形后和初始孔隙比；各参数的获取同公式(7)、(8)。

将延安市Q3黄土进行重塑，当初始孔隙比e0=0.726 3、压实度K=90%时，相应的干密度为1.58 g/cm3，当含水率w分别为13.3%、15.3%时，根据公式(3)～(6)可以得出相应的黄土参数mε0分别为5.92、4.90；psc分别为519.2、411.4 kPa；λ分别为0.061 3、0.068 7；κ为0.012 4。由此计算出的黄土e-p关系曲线与试验散点值的对比见图9。由图9可见，修正模型的计算结果与试验值有较好的吻合度，说明修正模型能够预估高填方工程黄土的变形沉降。

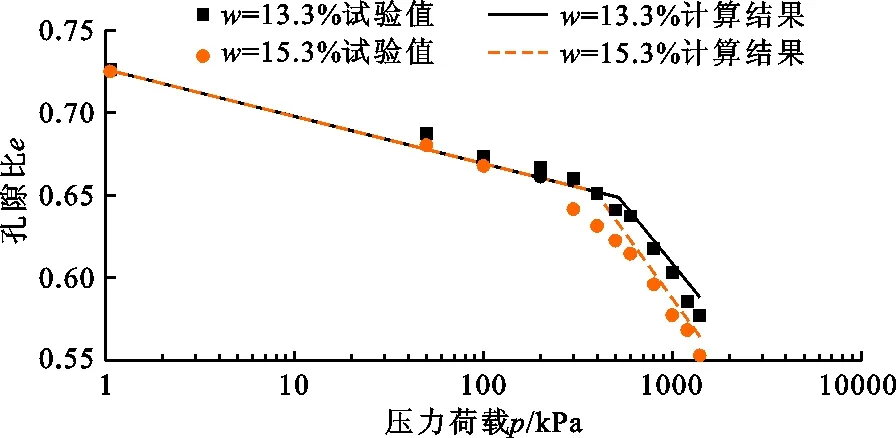
图9 黄土e-p关系曲线修正模型计算结果与试验值对比

5 结 论

(1)当黄土的压实度K一定时，其含水率越大则压缩曲线分布越“陡峭”；当黄土的含水率w一定时，其压实度越大则压缩曲线分布越“平缓”；相同干密度下重塑黄土的压缩曲线分布较原状黄土衰减更显著。

(2)随着含水率w的增大，黄土的结构屈服压力psc和初始结构性参数mε0呈非线性减小，压缩指数λ呈线性增大；随着重塑黄土压实度K的增大，黄土的结构屈服压力psc和初始结构性参数mε0呈增大趋势，压缩指数λ呈减小趋势；随着压实度的增大，含水率的变化对黄土压缩指数λ和初始结构性参数mε0的影响逐渐减小，而对结构屈服压力psc的影响仍较为显著；原状黄土的初始结构性明显大于重塑黄土，含水率变化对原状黄土初始结构性的削弱影响明显大于重塑黄土。

(3)基于试验结果，构建了黄土压缩指标与初始结构性参数之间的线性函数模型，分析发现，psc随mε0的增大而线性增大；λ随mε0的增大而线性减小；弹性指数κ随干密度ρd的增大而非线性减小。

(4)考虑黄土的结构性参数，建立了修正的黄土结构性一维压缩模型，给出了上覆填土与下覆原状黄土的沉降预估模型，并结合试验数据进行了对比验证。但由于试验样本有限，后期将进一步开展相关试验工作验证修正模型的工程适用性。