基于微分变换的湿地植物高光谱全氮反演

黎 舟，杨思林,2*，刘云根,2，王 妍,2，张 超，肖羽芯，徐红枫

1. 西南林业大学生态与环境学院，云南 昆明 6502242. 西南林业大学，云南省山地农村生态环境演变与污染治理重点实验室，云南 昆明 6502243. 西南林业大学林学院，云南 昆明 650224

氮素作为植物生长必需元素，参与植物体内重要化合物的合成代谢，直接影响植物的生长发育[1]. 相关研究[2-4]表明，利用水生植物监测河流湖泊的富营养化程度，在水体富营养化条件下，其生长变化情况与组织中的氮素含量有关. 云南省作为我国湿地资源众多的省份，目前生态环境日益恶化，引起了一系列湖泊水环境问题. 因此，如何最大程度地实现对湿地植物养分含量的监测评价，并根据其污染状况进行生态修复和防治是目前亟需解决的问题[5].

高光谱遥感是一种在可见光和红外波段范围内获取更高分辨率的窄波段连续光谱图像的技术，目前被广泛运用于生态、地质、海洋等各领域[6]. 高光谱遥感实时、高效和低成本的优势为监测诊断植物生化参数提供了有效手段[7-9]. 高光谱遥感技术应用于湿地植物生化参数的测定研究中，其中对芦苇(Phragmites australis)、香蒲(Typha angustata)和水稻(Oryza sativaL.)的研究居多. 郭超凡等[10]基于湿地植物叶片原始光谱及一阶导数光谱构建模型定量估算了芦苇和香蒲的叶片全氮含量，发现芦苇反射光谱所建立的模型精度均高于香蒲. Liu等[11]利用芦苇叶片的汞含量和反射光谱作为数据源，通过回归分析法研究二者关系，结果表明，连续小波变换多元线性逐步回归适合估算叶片低含汞量，差分光谱指数偏最小二乘回归更适合估算叶片高含汞量. 孙小香等[12]以不同施肥处理下的晚稻为研究对象，基于水稻冠层反射光谱、三边参数以及光谱指数，构建了与水稻冠层全氮含量的多元线性与BP神经网络预测模型. 现阶段植被含氮量高光谱遥感反演主要是对已有反演方法的运用，反演方法主要包括波谱指数法、回归分析法和辐射传输模型分析法，回归分析法在反演应用中最为广泛[13-14].

该文以云南省大理西湖湿地公园优势植物芦苇和茭草(Zizania caduciflora)为研究对象，结合实测全氮含量和反射光谱数据，通过不同的微分变换分析，构建最佳波段与叶片全氮含量的估算模型，预期在模型构建中明确光谱数据与生化参数间的因果关系，探究预测植物叶片全氮含量的最优模型，为湿地植物生长的遥感监测提供理论参考.

1 材料与方法

1.1 研究区概况

大理西湖湿地公园位于云南省大理白族自治州洱源县右所镇西部(26°00′N～26°02′N、100°01′E～100°04 ′E)，为原生湖泊湿地，主要包括张家登村、清水塘村、东登村、中登村、南登村和海塘村，属北亚热带高原季风气候，具有干湿季分明、区域小气候明显的特点. 西湖湖面面积3.3 km2，平均水深1.8 m，最大水深3.3 m. 湿地内挺水植物分布面积最广且最为典型，包括芦苇和茭草，因此该文主要对芦苇和茭草进行植物高光谱全氮反演探讨.

1.2 湿地植物光谱采集及全氮含量的测定

选取大理西湖湿地公园内的芦苇、茭草作为光谱采集对象，采集时间为2020年8月21—22日. 样地大小为1 m×1 m，将整个样地划分为16个0.25 m×0.25 m的样方，每个样地依据实际情况选择一个样方实地测量光谱并采集植物样品. 根据两种湿地植物在清水塘村、海塘村等5个村落的分布情况，均匀设置25个芦苇样地、28个茭草样地.

植物光谱反射率测量仪器采用 便携式地物光谱仪(FieldSpec3，ASD，美国)，光谱范围为350～2500 nm. 野外实地测量选在晴朗无风的天气，测量时间为10:00—16:00. 受太阳光强度、水汽等影响，光谱波段存在毛刺和噪声的现象，删除明显的3个水分吸收带(1350～1450、1750～1950、2350～2500 nm). 利用Origin 2019b软件对光谱曲线进行平滑，使其更趋近于真实值. 植物样品采集完毕，取相应样品利用凯氏法测定植物叶片全氮含量.

1.3 微分光谱分析

微分光谱法即导数光谱法，是在原始光谱反射率的基础上进行基本数学变换、一阶微分变换和二阶微分变换. 建模结果表明，基本数学变换后的植物光谱反射率与全氮含量之间没有任何波段达到极显著相关性水平，微分变换更有利于凸显光谱特征的细微差异. 故该研究主要针对原始反射率(R)及其对数倒数平方根立方根这5种基本数学变换进行一阶微分和二阶微分运算(分别用 ′ 和 ″表示)，共计10种光谱变换方法.

1.4 模型构建

通过植物光谱反射率微分变换与全氮含量的相关性分析，提取与全氮含量相关性较高的光谱变量参与估算建模. 按照7∶3的比例，芦苇的训练集和验证集样本数量分别为17、8，茭草分别为20、8，随机选取植物样本作为建模数据及验证数据. 建模方法采用单变量回归、偏最小二乘回归和BP神经网络.

在单变量模型构建过程中，采用一次函数、二次函数、三次函数、指数函数、对数函数、复合函数、生长函数、逆函数、幂函数模型，通过比较分别选择精度最高的单变量函数模型作为每一种光谱变换方法对应的最后结果. 在多变量模型构建过程中采用偏最小二乘(PLSR)模型和BP神经网络模型，多变量模型随机抽取7份作为训练集的数据，通过相关性分析选取相关系数绝对值最大的4个极值点，并对入选波段按其相关系数绝对值大小进行排序，由此筛选出原始光谱及其变换光谱与全氮含量相关性最强的4个波段反射率参与建模. PLSR模型用于查找两个矩阵之间的基本关系，它是主成分分析、典型关联分析和多元线性回归这3种基本算法相结合的产物，因此被广泛运用于建模及预测[15].BP神经网络模型是一种多层前向神经网络模型，在现有建模方法中，主成分分析、随机森林算法、支持向量机、人工神经网络，人工神经网络建模效果最优，BP神经网络属于人工神经网络的一种[16-18].该文中BP神经网络模型首先利用多元线性回归算法筛选相关性最强的自变量，再利用拟牛顿法进行参数优化，最终构建最优模型[19]. 模型构建主要运用Python编程语言完成.

1.5 模型验证

采用决定系数(r²)和均方根误差(RMSE)评价模型精度.r²值愈趋近于1，表明模型预测能力越高.RMSE值用于衡量实测值及预测值的差异，值越小表示模型更具稳定性.

2 结果与讨论

2.1 植物叶片全氮含量与光谱反射率的相关性

所有采样点植物叶片的原始光谱和微分变换光谱反射率与植物全氮含量的相关性分析(见图1、2)表明，茭草全氮含量与原始光谱反射率(R)在873～951、1002～1144 nm达到了显著相关性水平(P＜0.05).茭草原始光谱反射率与全氮含量的相关性在整个波段范围内正负相关不断交替，芦苇整体上则呈正相关趋势，能反映茭草和芦苇全氮含量特征的敏感光谱主要集中在可见光(350～760 nm)、近红外波段(760～1350 nm). 在可见光、近红外波段范围内，茭草全氮含量受到植物叶绿素、细胞壁厚度差异等的影响，相关性曲线形态出现出几处波谷；在短波红外(1450～2350 nm)范围内，茭草全氮含量和原始光谱反射率没有达到显著相关性水平. 芦苇原始光谱反射率(R)与全氮含量在整个波段范围内没有任何波段达到显著相关性水平，微分变换更有利于去除噪声对芦苇光谱的影响.

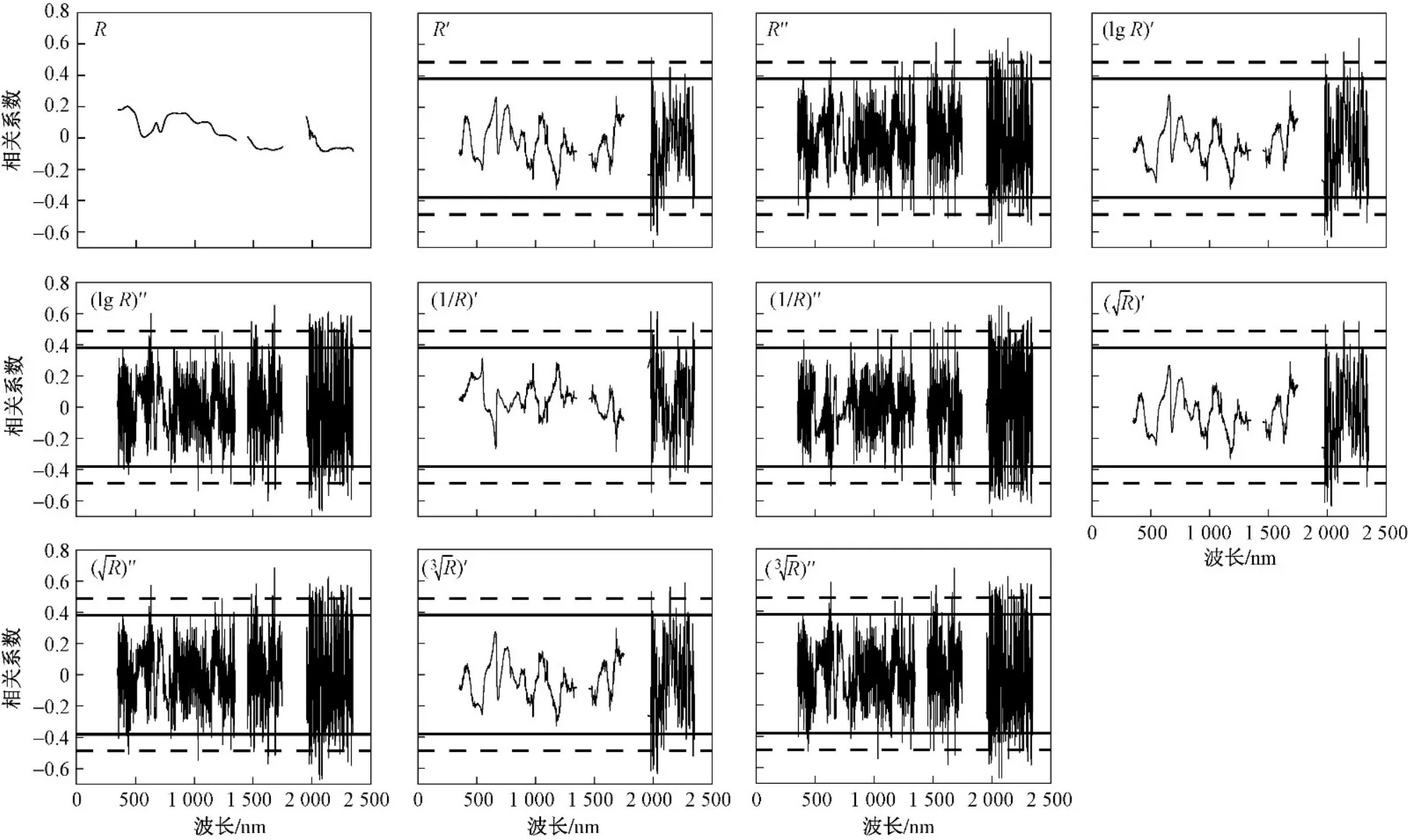
图1 微分光谱值与芦苇全氮含量的相关性Fig.1 Coefficients correlation relating differential spectral values and total nitrogen content of Phragmites australis

通过10种微分变换光谱去噪处理,得到两种植物叶片全氮含量与微分变换光谱反射率在整个波段范围内的相关性水平显著提高，经过二阶导数变换的曲线变化较一阶导数更为剧烈，波峰波谷的数量明显增加. 芦苇、茭草叶片反射光谱和全氮含量的一阶导数变换相关性在可见光近红外波段内体现得不够突出，均未达到显著(P＜0.05)及极显著水平(P＜0.01)；反观二阶导数变换相关性，在可见光近红外波段内，茭草反射率与全氮含量的相关性共有77个波段达到了极显著水平(P＜0.01)，在1190 nm处相关性最强，相关系数高达—0.80. 芦苇反射率与全氮含量的相关性共有3个波段达到了极显著水平(P＜0.01)，在632 nm处相关性最强，相关系数为0.60.在短波红外范围内，植物光谱受叶内水分含量的控制，水分含量降低，光谱反射率升高. 茭草R′′反射率与全氮含量的相关性在短波红外波段范围内共有69个波段达到了极显著水平(P＜0.01)，在2105 nm处相关性最强，相关系数高达0.77；芦苇R′′反射率与全氮含量的相关性在短波红外波段范围内共有43个波段达到了极显著水平(P＜0.01)，在1682 nm处相关性最强，相关系数为0.70. 这些相关性较强的敏感波段为大理西湖湿地公园植物芦苇、茭草全氮含量的估算预测提供了最直接的科学依据.

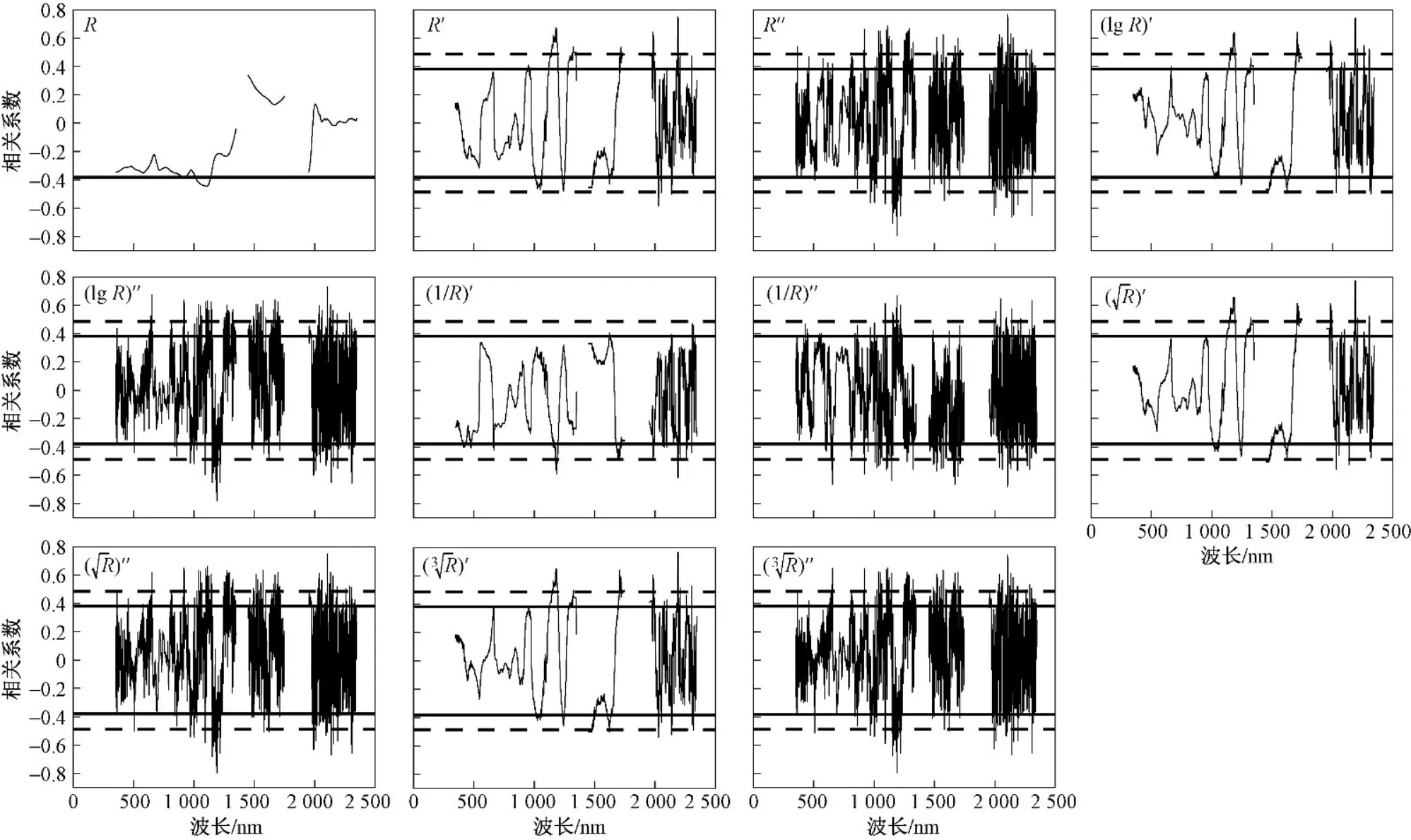
图2 微分光谱值与茭草全氮含量的相关性Fig.2 Correlation relating between differential spectral values and total nitrogen content of Zizania caduciflora

2.2 植物全氮含量高光谱估算模型构建与精度比较

2.2.1 不同微分变换下的植物全氮含量单变量模型构建与精度比较

单变量回归模型建模结果(见表1)表明，绝大多数函数模型符合精度要求. 由于芦苇、茭草叶片R、R′、R′′的反射率建模效果不佳，故在模型构建中予以剔除. 芦苇反射率与全氮含量所建立的三次函数 模型的精度最优，评价建模精度的r2和RMSE分别为0.67、1.50，评价验证精度的r2和RMSE分别为0.78、2.78；茭草反射率与全氮含量所建立的二次函数建模精度最高，其r2和RMSE分别为0.66、2.23，反射率与全氮含量所建立的二次函数验证精度最高，其r2和RMSE分别为0.62、3.04. 光谱信息经过微分变换后，模型精度比原始反射率模型精度得到了不同程度的提升，其模型完全可以用于估算植物叶片全氮含量.

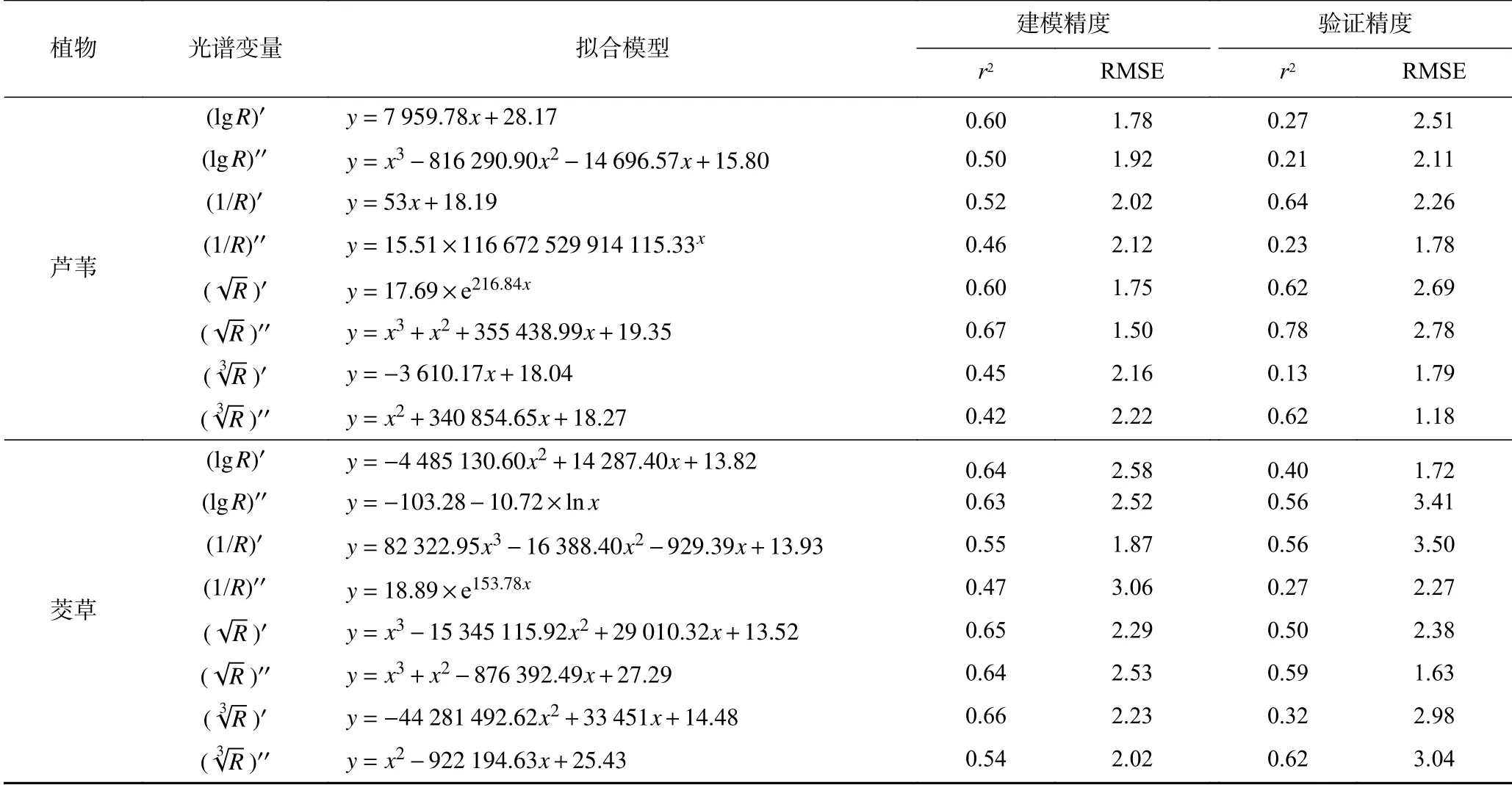
表1 植物光谱变量(x)与全氮含量(y)单变量的最优估测模型Table 1 Univariate optimal estimation models of plant spectral vlues (y) and total nitrogen contents (x)

单变量模型仅考虑单一变量参与建模，目前研究对象主要针对土壤及农作物，对于湿地植物的研究较少[20-21]. 有报道[22]指出，经过简单数学变换、导数变换、小波变换3种反射率变换方法，建立茭草生物量的估算模型，其多元线性回归模型精度高于单变量模型精度. 但在所有光谱变换下的茭草生物量回归模型中，最优模型为单变量模型的居多；崔小涛等[16]通过比较不同生育期的油菜叶片光谱参数与叶绿素含量的单变量最优估算模型，可见蕾薹期利用MCARI/OSAVI(植被指数)建立二次函数模型可达到拟合效果，表明油菜在蕾薹期吸收氮磷钾养分充足.单变量模型参与建模的变量单一，但模型表达式多样化，易于筛选适合研究对象光谱参数及其理化参数的最优拟合模型.

2.2.2 不同微分变换下的偏最小二乘回归模型构建与精度比较

光谱信息经过微分变换后，利用偏最小二乘法筛选最优模型. 结果(见表2、3)表明模型精度得到了整体的提升，而且在二阶导数变换处理下体现得更为突出. 芦苇叶片R′′反射率与全氮含量所建立函数的模型精度达到最优，其评价建模精度的r2和RMSE分别为0.49、1.70，评价验证精度的r2和RMSE分别为0.45、2.25；茭草叶片反射率与全氮含量所建立的函数模型精度达到最优，其评价建模精度的r2和RMSE分别为0.66、1.83，验证精度r2和RMSE分别为0.74、2.39. 由此可见，二阶导数变换更有利于提取植物叶片光谱中的敏感特征.

表2 芦苇光谱变量(x)与全氮含量(y)的偏最小二乘回归模型Table 2 Partial least squares regression model of spectral values (x) and total nitrogen contents (y) of Phragmites australis

多变量模型融合了多个敏感波段特征，在很大程度上缓解了“多重共线性”的问题，提高了模型的适用性及稳定性[23-24]. 多变量模型比单变量模型的研究范围更为广泛，不仅涉及土壤、农作物及湿地植物，在中药领域也应用甚多[25-27]. 有报道[10]证实，运用偏最小二乘法分别构建芦苇及香蒲原始光谱、一阶导数光谱的叶片全氮含量回归模型，芦苇模型的精度均高于香蒲. 这表明芦苇对氮的吸收能力强于香蒲，更能反映其所处的生境特征. 偏最小二乘法避免了传统生化参数光谱反演中存在的一些问题，有效地提高了回归精度.

表3 茭草光谱变量(x)与全氮含量(y)的偏最小二乘回归模型Table 3 Partial least squares regression models of Zizania caduciflora spectral values (x) and total nitrogen contents (y)

2.2.3 不同微分变换下的BP神经网络模型构建与精度比较

BP神经网络模型可以很好地解释非线性问题，通过反向传播算法不断调整网络的权值和阈值，以达到满足最小误差精度的条件[28]. 但在模型构建中，隐含层神经元数过多或过少，均易导致过拟合现象，应根据神经元数M≤2n+1(n为输入变量个数)来逐步调节，最终确定最优神经元数[20].

将植物光谱变量所有波段反射率作为BP神经网络模型的输入层，隐藏层为100个，隐藏层的激活函数为修正线性多元函数，神经元为20个，全氮含量作为输出层，构成估测模型的整个网络架构. 参数优化算法采用拟牛顿法，并对光谱数据进行量纲化处理[29]，以降低对预测精度的影响；最大迭代轮数设置为100，学习率为0.1，网络性能目标为0.0001；以7:3的比例对芦苇和茭草全氮含量进行网络训练及样本预测，预测结果见图3.

图3 微分变换后反射率与不同植物全氮含量的BP神经网络预测结果Fig.3 BP neural network prediction of differential transformation reflectance and total nitrogen content of different plants

2.3 各模型效果与模型精度比较

根据单变量模型及多变量模型的预测精度，BP神经网络模型部分结果精度不达标，故剔除. 以BP神经网络模型光谱变量为基准，比较单变量模型及多变量模型预测精度，该研究仅针对于芦苇、茭草叶片的( lgR)′、( 1/R)′和 ( 1/R)′′光谱变量开展讨论.

如表4所示：①芦苇全氮含量单变量模型的最优精度高于茭草，最优模型为1726 nm波长处 ( 1/R)′反射率所建立的一次函数，r²为0.64，RMSE为2.26.②BP神经网络模型预测能力大于单变量模型和偏最小二乘模型预测能力，芦苇和茭草BP神经网络模型的r²高达0.96，极大地提高了模型精度和预测性能.

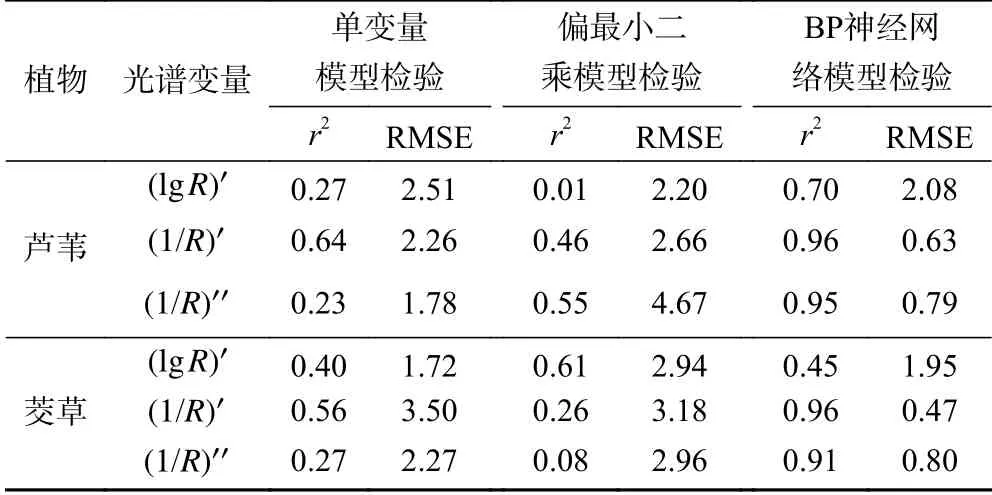
表4 植物全氮含量估测模型的精度检验结果比较Table 4 The comparison of test precision of different models for total nitrogen content

综合考虑，芦苇及茭草全氮含量(y)最优的单变量模型分别为726 nm波长处的 (1/R)′， 反射率(x1)所建立的一次函数、1884 nm波长处的 (1/R)′反射率(x2)所建立的三次函数，其样本精度高，整体拟合较好，分别如式(1)(2)所示：

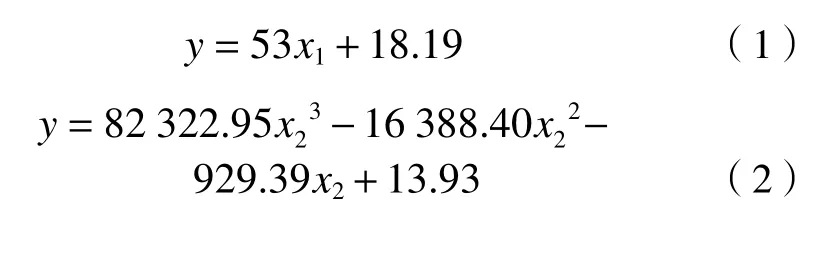
总体而言，目前对于湿地植物的高光谱遥感研究较少，探讨也不够深入 . 该研究中植物采集时间为8月底，处于植物生长花期，受水生植物腐解过程中物质释放规律对水体水质及污染治理的影响较小[30]. 有学者指出，随着季节更替，湿地形成了明显的丰水期和枯水期，枯水期水质波动大且全氮含量高[31]. 水生植物净增生物量与全氮含量富集率相关性较高，其全氮含量富集贡献率为50.23%～80.71%，其他作用对全氮的去除率为19.29%～49.77%[32]. 相关研究[33-35]表明，未来的湿地植物高光谱生化参数建模可根据植物不同的生育期和湿地降雨期的季节性结合植被指数、位置特征参数、面积特征参数等角度，以达到筛选高精度光谱参量的目的. 另外，实地光谱采集容易受现场环境的限制，在有条件的情况下可采用室内光源测定反射光谱，不仅环境时间可控，测定数据波段也更加完整.

3 结论

a) 从相关性分析来看，芦苇及茭草叶片的变换光谱反射率与全氮含量的相关性均达到了极显著性水平(P＜0.01). 不同形式的光谱变换增强了植物全氮含量与光谱变量的细节特征，二者的短波红外波段相关性强于可见光近红外波段. 芦苇变换光谱反射率与全氮含量相关性的最优光谱参量为二阶微分(R′′)反射率，在1682 nm处相关系数达到0.70；茭草最优光谱参量则为平方根二阶微分反射率，在1190 nm 处相关系数达到—0.80.

b) 不同植物类型相比，利用茭草变换光谱反射率与全氮含量所建立的单变量和偏最小二乘回归模型建模精度均高于芦苇.

c) 不同回归模型相比，芦苇和茭草全氮含量与变换光谱反射率所建立的BP神经网络模型的精度最高，r2均为0.96，RMSE分别为0.63、0.47，是建立湿地植物光谱与叶片全氮含量关系的最优模型.