Geo Gebra软件在物理问题表征中的应用*

龚圣卿 林 钦(福建师范大学物理与能源学院 福建 福州 350108)

表征是问题解决的一个中心环节.认知心理学家Simon指出，“如果一个问题得到了正确表征，可以说它已解决了一半.”[1]美国著名的数学家斯蒂恩也曾说，“如果能用图形表征特定问题，那么思想就对这个问题有了整体把握，就可以找到创造性地解决问题的办法.”[2]

在现实教学中，很多学生学习物理都有这样的感受，老师上课讲的物理规律、定理以及例题、习题等好像都听懂了，可是一旦之后碰到类似的物理问题，又变得茫然无措了.拿到题目时无从下手、不知所措，很多学生就直接开始套用相关公式，最后代数计算结果，如果最后发现错了，再换另一个公式接着尝试，就这样盲目的尝试错误[3].显然，学生解决物理问题的步骤变成了读题、接着套用物理公式、最后进行数学演算这一机械过程.

究其原因是多方面的，其中很重要的原因是解决问题的表征形式影响着学生的思维方式，学生学习物理变成了只习惯于用文字表征、数学表征，而对“问题表征”中图形表征、方法表征等能力却显得比较弱，导致学生不能有效解决物理问题[4].对问题做什么样的表征，这种表征是否适宜，直接影响解决问题的难易、快慢和成败.

在物理表征教学中，GeoGebra软件有其自身独特的优势.例如滑块木板模型往往让学生感到头疼，认为该过程和情境复杂.若在教学过程中，利用GeoGebra将动态过程可视化地呈现出来，同时配合滑块木板运动的速度-时间图像，如图1所示，可以使学生更容易理解该情境的物理过程，教学效果往往更佳.

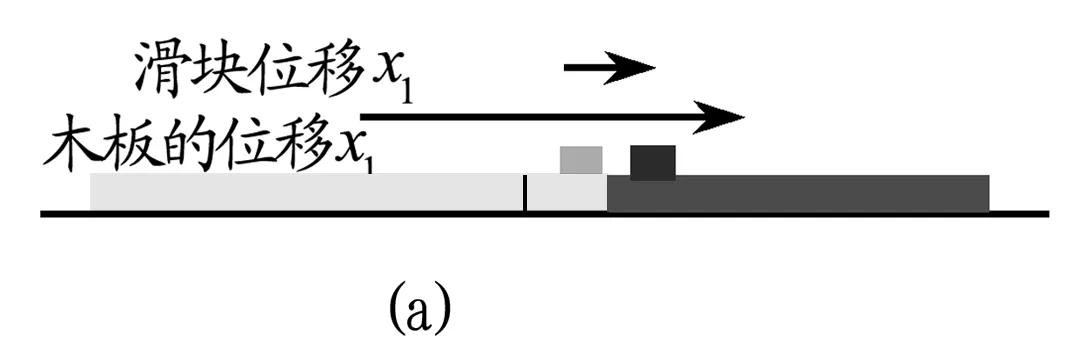
图1 滑块木板模型

目前GeoGebra软件在物理教学中的应用情况大致可分为4大类:

(1)在物理概念教学中的辅助教学应用，文献[5]利用该软件进行简谐运动和机械波物理课堂教学.

(2)辅助习题教学应用，文献[6]针对一道高考题，对等量同种电荷连线中垂线上场强进行研究.

(3)辅助物理实验教学应用，文献[7]将该软件运用在平抛运动实验数据的可视化处理.

(4)辅助物理问题探究等，文献[8]利用GeoGebra软件模拟行星现象.

笔者认为GeoGebra软件在物理教学的各方面应用过程中的优势主要体现在分析动态过程、探讨临界状态，绘制函数图像、理解物理规律，图形维度转换、突破思维障碍等3个方面.

1 分析动态过程探讨临界状态

临界状态往往是极值出现的状态，该状态涉及的物理过程往往比较复杂，考查学生推理能力和分析综合能力，利用图形进行表征，可以帮助学生巧妙地解决临界状态问题.

例如在探究三共点力动态平衡问题时，如图2所示，“∠”形铁架中，∠ABO=60°，铁架中放一钢球，系统恰好静止于实线位置(钢球与OB边接触，AB边水平).现使铁架绕水平转轴O逆时针缓慢转过90°至虚线位置，不计一切摩擦，则该过程中钢球受到BA和OB的弹力变化情况如何.

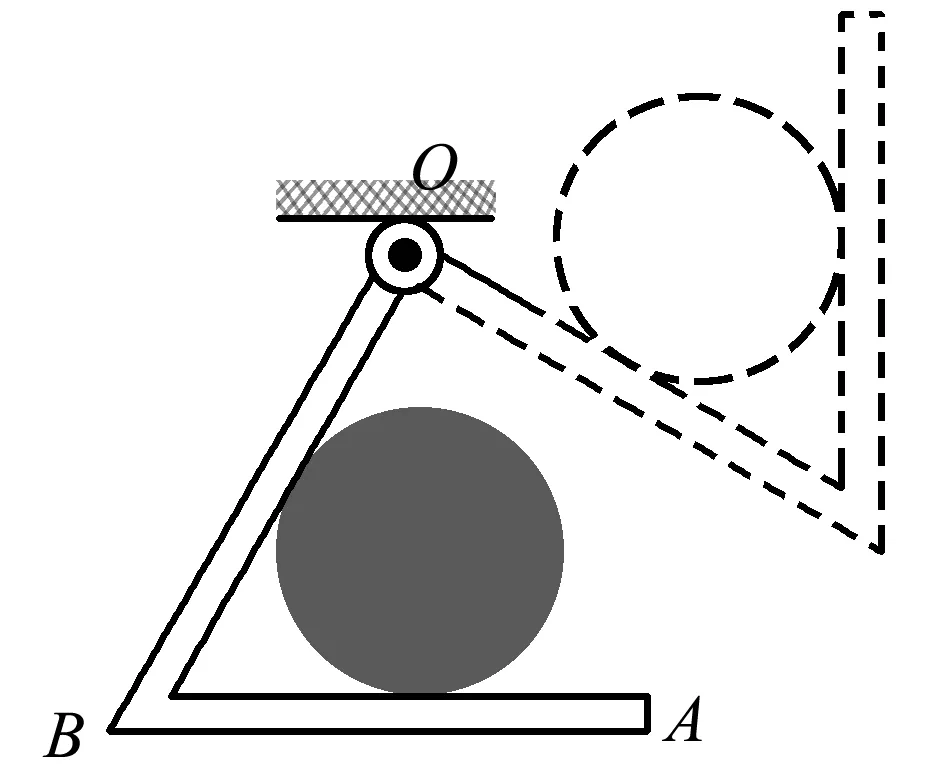
图2 三共点力动态平衡问题情境图

铁架绕O点转动某一角度，钢球受力如图3所示，其中铁架夹角为α，铁架绕O点转过的角度为β.在GeoGebra中，利用力的合成的思路，绘制出铁架转动过程动态图形，如图3所示.

图3 钢球受力分析图

通过β调节铁架绕O点转动的角度，N1和N2的大小可在动态文本工具中同步显示出来.

由于铁架形状保持不变，N1和N2的夹角保持不变，合力始终与重力平衡，根据“同一弦所对应的圆周角相等”的规律建立如图4所示的辅助圆.在图3矢量三角形CDE中，两弹力的夹角α，它们的夹角α始终对应钢球所受合力F合，绘制出辅助圆，如图4所示，在辅助圆中，E点为在圆周上的动点，移动点E，可以改变角度β，分析铁架绕O点转动过程两弹力大小的变化趋势.

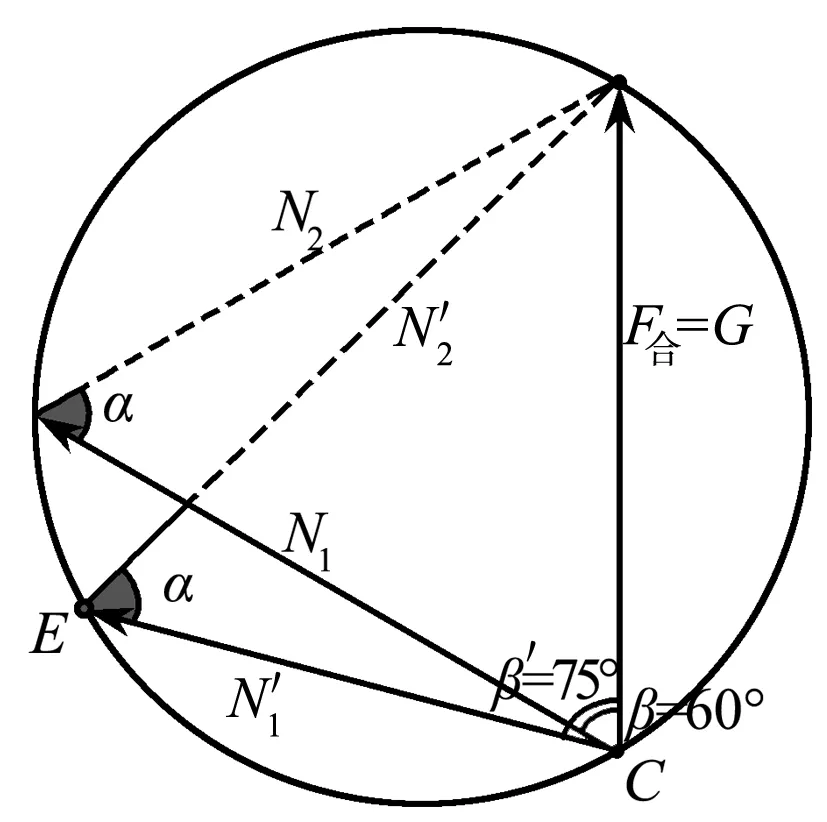
图4 辅助圆

斜抛运动中，可利用GeoGebra将斜抛运动轨迹可视化，分析动态变化的斜抛运动轨迹，进而得出斜抛运动结论.

如图5所示，调节初速度或抛射角，斜抛运动轨迹即可发生相应的改变，变化的轨迹也可以记录下来，进而分别探究初速度、抛射角度与斜抛运动的射程和射高的关系.

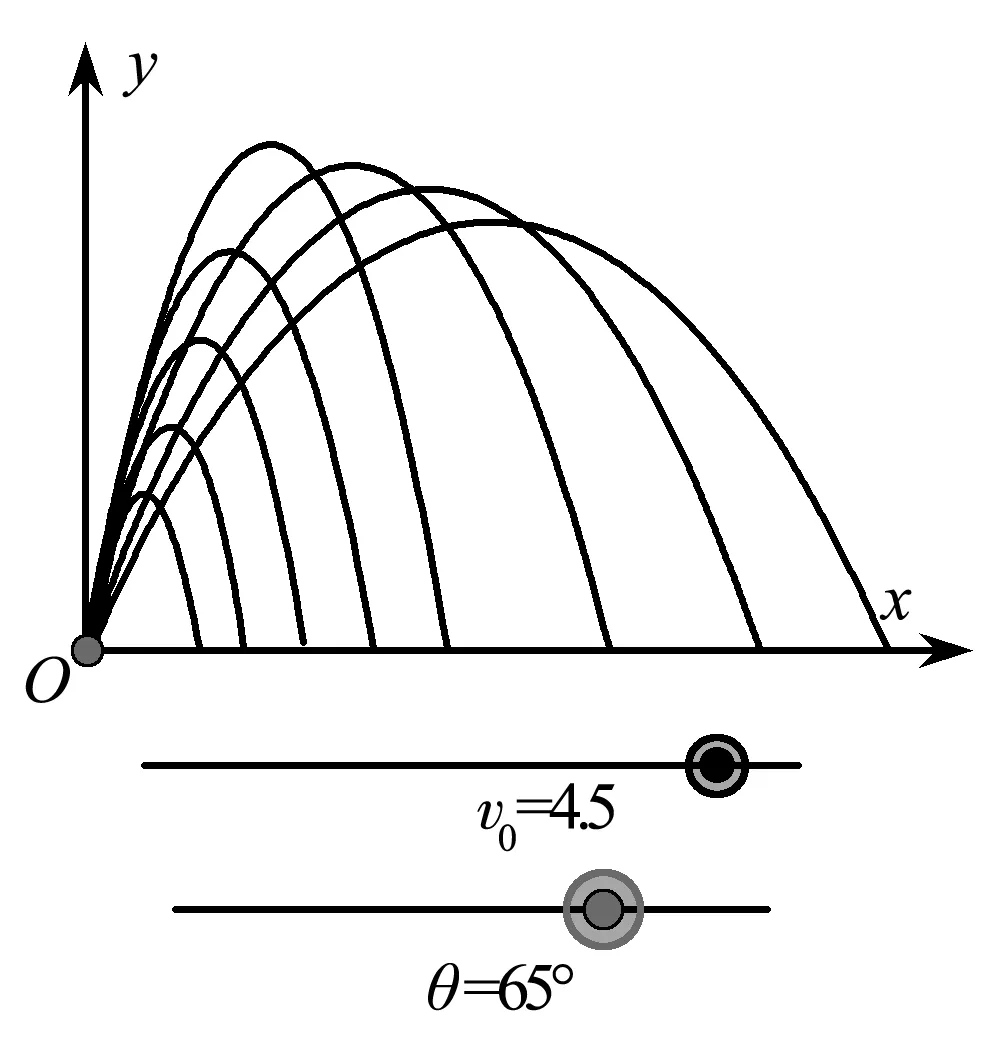
图5 抛射轨迹

如图6所示，通过调节抛射角θ滑动条，实时读取抛射轨迹的长度、轨迹的边界与水平轴所围面积大小、射程的长度等数值，比较抛射角θ取何值时三者数值分别达到最值.且在图7中，以抛射角为横坐标，分别以面积大小、轨迹长度、水平射程长度为纵坐标，绘制出三者与抛射角θ的函数图像，图像能够直观地看出抛射角θ存在一个临界值，使得该三者存在最大值.

图6 抛射角度与轨迹长度、面积、射程关系

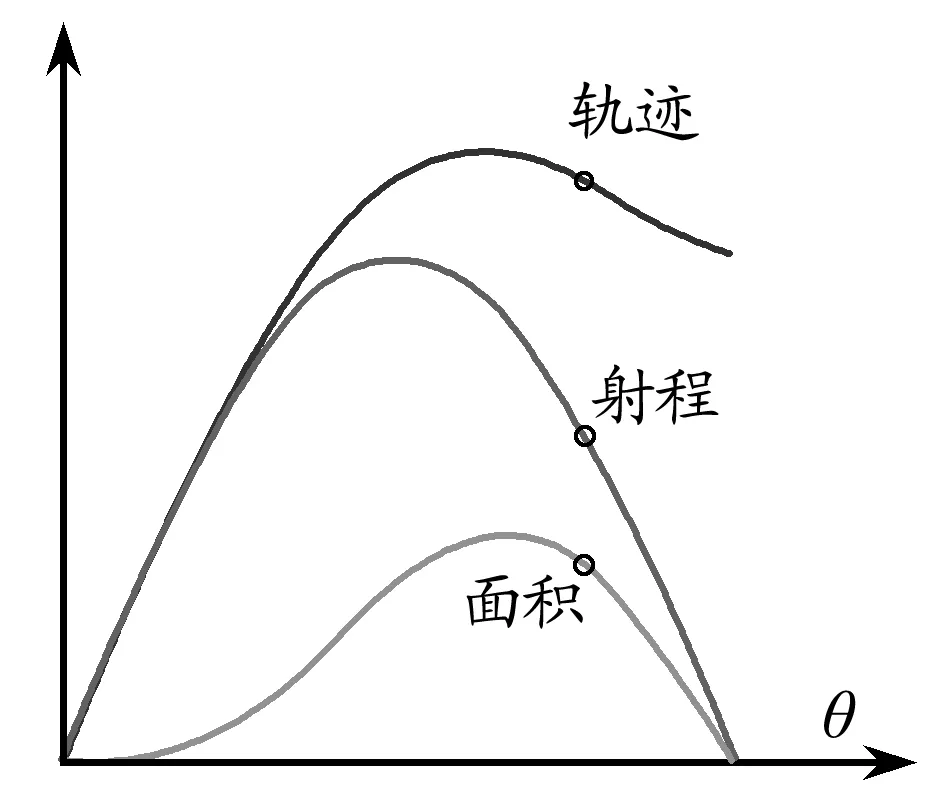
图7 关系曲线

利用GeoGebra绘制出科学准确的物理图形，可显现出物体变化和运动的动态过程出现的关键点、转折点、临界点.在解决物理问题时，画出图形的过程，形成物理图景，往往需要形象思维活动的参与，可以有效帮助学生构建物理模型，培养学生形象思维能力.

2 绘制函数图像理解物理规律

物理教学中离不开数学思想的渗透，物理规律的得出往往也需要列出物理量之间的数学关系式，利用恰当的函数图像进行分析、表达，进而通过图像找出其表达的物理内容，记忆物理规律.

在“∠”形铁架例题中，为了更好地说明两分力的大小变化情况，还可以利用正弦定理进行辅助分析.图3可知

其中θ=120°-β，利用GeoGebra绘制出两个力N1和N2与转动角度β之间的关系图像，如图8所示，观察函数图像可以发现，铁架在转动过程，两个力与旋转角度的关系存在着临界状态：当铁架转动时，N1先增大后减小；铁架旋转角度为零时，N1大小等于重力，此时N2值为零；铁架旋转角度为30°时，力N1达到最大值，N2先增大后减小；铁架旋转角度为90°时，力N2达到最大值；铁架旋转角度为120°时，N2大小等于重力，此时N1值为零；其中，铁架旋转角度为60°时，N1和N2大小都等于重力.

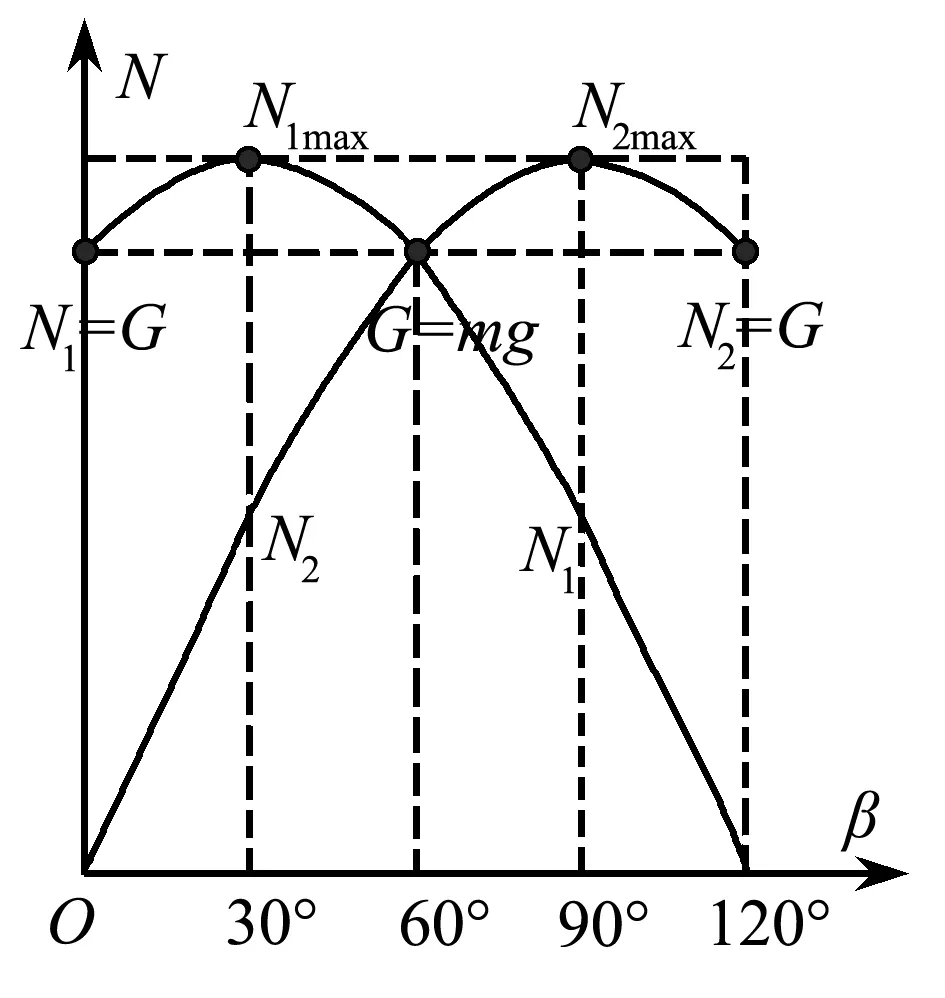
图8 作用力与转动角关系曲线

在探究分压电路中各部分电流变化规律时，学生往往难以理解数学表达式的结果.例如，在图9电路图中，若滑片P将电阻R2分为两部分，设右部分电阻为r，则滑片从b端滑至a端，A，B处的电流分别如何变化？

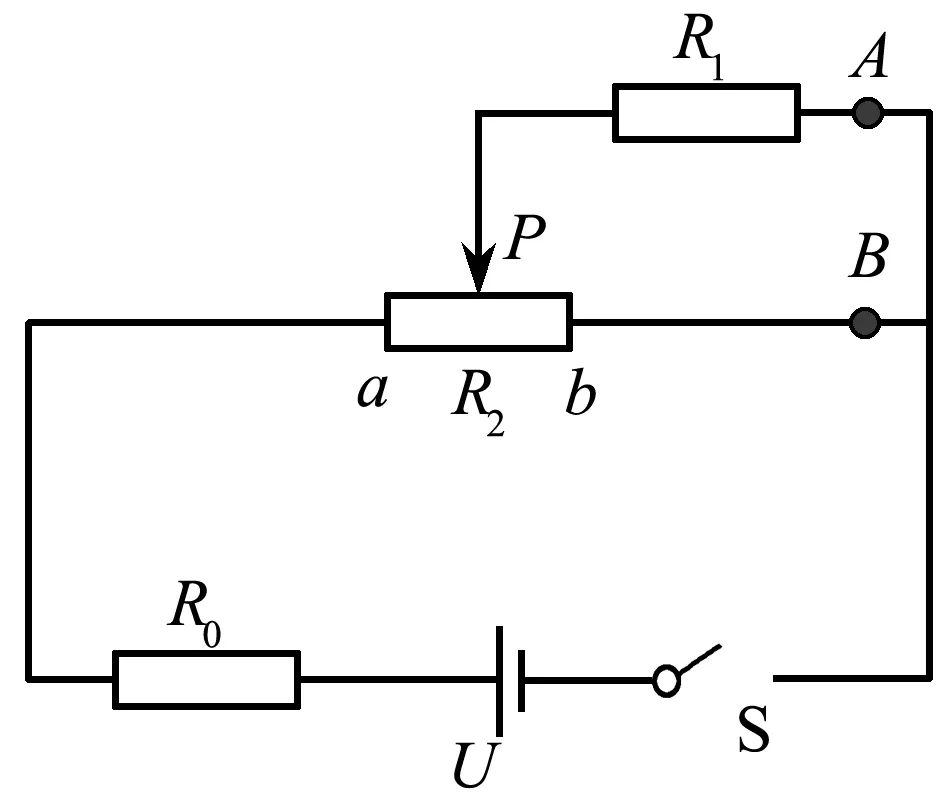
图9 电路图

学生在解答此类问题时，常常利用“程序法”“特殊值法”定性分析，有时却不能得出结论，究其本质，还需要列出该过程的函数关系式，进行定量分析.根据欧姆定律列出电流IA与电阻r之间的关系

电流IB和电阻r之间的关系

观察函数关系式发现，对于给定的电源U和电阻R0，R1，R2，输出各支路的电流与电阻r相关，但它们之间存在什么样的关系，只从表达式中不容易得出结论.可根据函数表达式，利用GeoGebra以数化形，可以较为直观地分析出电流随滑动变阻器的变化情况.

在GeoGebra输入框中分别输入电流IA和IB与电阻r之间的函数关系，分别得到电流IA和IB与电阻r的静态曲线，开启静态曲线跟踪功能，改变R0，可得到不同R0对应的静态曲线.同时分别创建A，B点，两点分别为电流IA和IB与电阻r函数上的动点，启动动画按钮，观察动点A，B在静态曲线上运动，动点坐标显示电阻r与对应电流值，如图10所示.

观察函数图像可知，滑片从b端滑至a端过程，电流表IA的读数随着r值的增大而单调递增.而电流IB的单调性却没有唯一确定，当R0较小时，电阻r增大，电流表IB的数值先减小后增大；当R0较大时，电流表IB的数值随电阻r的增大单调递减.可见电阻R0的大小影响着分压电路中滑动变阻器支路部分电流的单调性.

利用GeoGebra将物理公式和函数图像结合起来，引导学生理解公式和数学图像背后的物理意义，帮助学生更直观地从整体上把握规律.在解决物理问题时，往往涉及列方程等数学步骤，恰当进行逻辑推理思维活动，以数形结合的方式，加深数学表征的理解，得出物理结论，有利于培养学生的物理运算能力和推理思维能力.

3 图形维度转换突破思维障碍

物理教学中含有许多抽象的物理知识，教师在课堂讲解过程常以二维平面中画图为主，学生理解起来费劲.因此，我们在画图的过程中“升维”能够有效突破学生思考过程的思维障碍，提高学生的抽象思维能力，促进问题的解决.

例如在水平桌面M上放置一块正方形薄木板abcd，在木板的正中央放置一个质量为m的木块，如图11所示.

图11 图形维度转换问题情境图

先以木板的ad边为轴，将木板向上缓慢转动，使木板的ab边与桌面的夹角为θ1，再接着以木板的ab边为轴，将木板向上缓慢转动，使木板的ad边与桌面的夹角为θ2(ab边与桌面的夹角不变).在转动过程中木块在木板上没有滑动，求转动以后木块受到摩擦力的大小.

如果把桌面称为水平面M，第一次转动θ1得到平面M′，将物体重力正交分解，如图12所示，第二次翻转θ2，得到平面M″，如图13所示，作平面M″的垂线N，第一次在水平面翻转θ1所产生的静摩擦力f1=mgsinθ1，第二次翻转时“等效重力”大小为mgcosθ1,第二次在斜面上翻转后所增加的侧向静摩擦力应为f2=(mgcosθ1)sinθ2，因此最后的摩擦力为

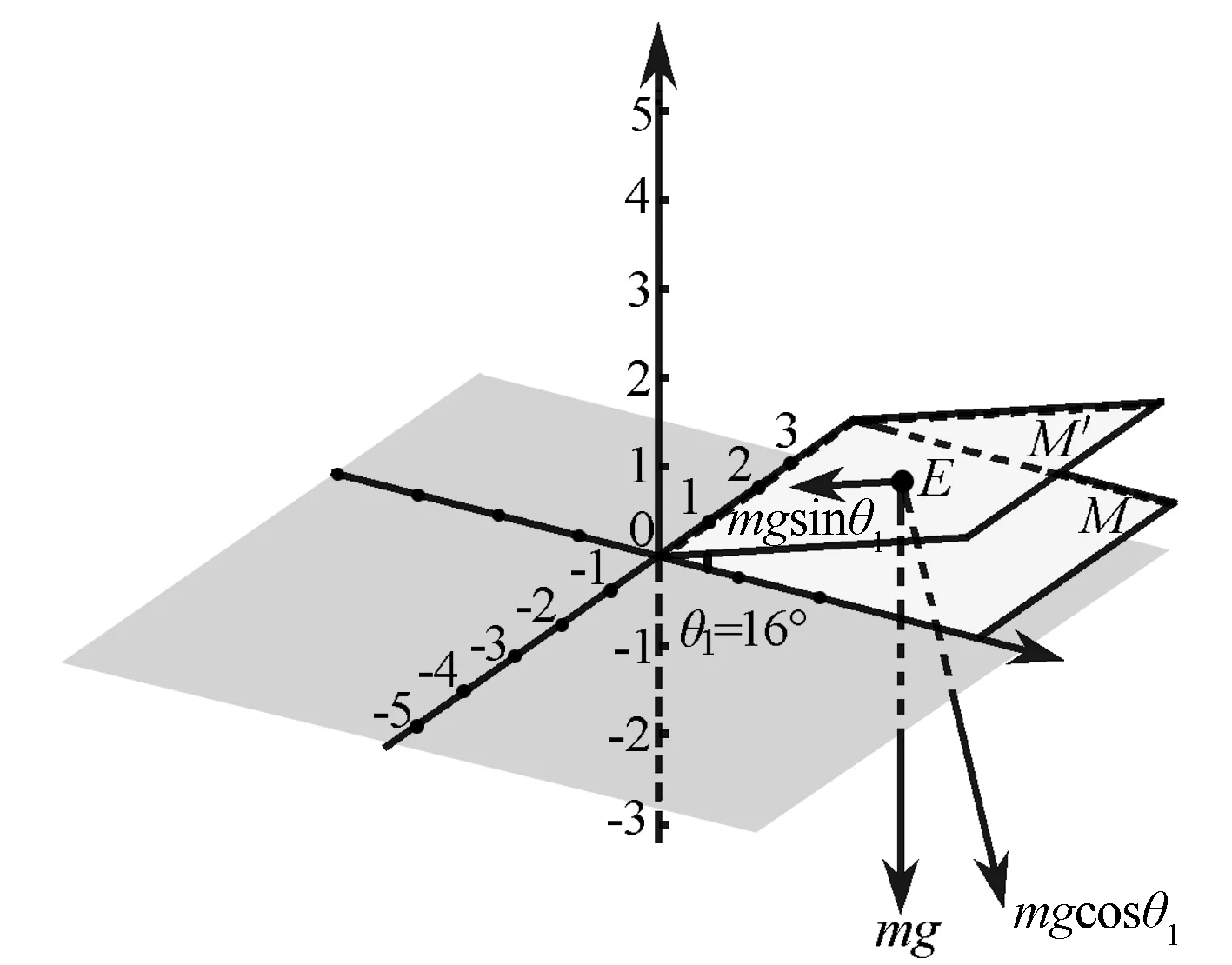
图12 翻转一次受力分析图

图13 翻转两次受力分析图

利用GeoGebra绘制出三维物理情境图，类比二维斜面时的受力分析，利用等效的原理进行力的分解是解题的关键.在解决物理问题时，只有正确运用科学的方法抓住问题的要害，才能找出解决问题的途径，类比、联想、等效、图解等都是常用的科学思维方法，学习和运用这些科学思维方法，进行恰当的分析思维活动，能够有效促进问题的解决.

综上所述，物理问题解决过程中，表征的难点和方式有所差异，但不同的表征过程都涉及了物理思维活动，思维活动贯穿问题解决的全过程[9].在平常的物理教学中，提高学生物理思维能力、物理想象能力、物理运算能力、运用科学方法能力等是有效促进问题解决的关键所在.