高度约束MHE算法在伪距单点定位中的应用
2022-05-19孙淑光杨祥源陈万通张巨联刘庆任诗雨
孙淑光,杨祥源,陈万通,,张巨联,刘庆,任诗雨
( 1. 中国民航大学 电子信息与自动化学院, 天津 300300;2. 中国民航大学 民航航班广域监视与安全管控技术重点实验室, 天津300300;3. 上海飞机设计研究院, 上海 201109;4. 上海航天电子技术研究所, 上海 201109 )
0 引 言
在进行伪距单点定位(SPP)时,数据往往采用后处理的方式,传统的精密卫星轨道及钟差产品存在时间延迟的问题,限制了SPP技术在实时场景中的应用[1]. 近年来,国际全球卫星导航系统(GNSS)服务(IGS)推出了一些具有高精度的GNSS精密定位产品,可以很大程度上消除卫星定位相关误差的影响[2].因此,一些相关研究重新聚焦于SPP技术.
SPP是仅利用一台接收机即可实现高鲁棒性的一种定位技术,而定位精度低仍是限制其实际应用的首要因素. 为进一步提高SPP的定位性能,近年来,研究人员发现一些场景下存在的先验信息可以用来增强单点定位性能.
文献[3]在SPP观测模型中加入了先验高度,将其作为准观测方程,用于加权最小二乘(WLS)计算,实验结果表明水平定位精度提高了42.84%. 文献[4]提出了先验海平面的高度约束精密单点定位(PPP)方法,并将约束方程通过差分处理实现线性化,实验结果表明附加高度约束的定位精度在垂直方向上提高了79%,三维方向上提高了67%. 文献[5]采用道路几何模型约束进行导航定位,将车辆的状态投影在地图段上,实验结果表明约束后的定位精度提高了31.4%.
传统的SPP解算方法通常采用最小二乘(LS)估计[6]. 而LS只考虑观测模型,不涉及系统状态模型,故所得定位结果通常显得粗糙杂乱. 因此,在一些研究中,研究人员引入了卡尔曼滤波(KF)算法,以实现KF算法的各种修改形式[7]. 其中,平滑约束卡尔曼滤波方法(SCKF)和无迹卡尔曼滤波方法(UKF)的出发点是先将非线性约束进行线性化,然后将其实现为完美测量[8-9]. 结果表明:上述方案所获得的估计值仅近似满足于非线性约束,而且非线性比简单的线性化过程会具有更好的匹配度[9]. 不同于KF算法,滚动时域估计(MHE)是把带约束的估计问题转化成优化问题,同时把施加在系统变量上的约束条件直接表述为优化问题中目标函数的约束,并通过在线滚动优化进行求解[10],是在约束条件下处理状态参数估计的最有效方法[11-12]. 同时MHE算法可能会用到KF所不包括的信息量,而且对非线性约束可以直接应用,无需线性化.
基于以上考虑,本文将非线性高度约束方程引入到约束MHE滤波算法中进行SPP的解算,从而实现定位精度的提高,获得更为平滑的定位结果.
1 SPP数学模型
SPP是以伪距观测为基础的一种定位方法,其伪距观测是指对所观测卫星和用户接收机之间距离的测量.
1.1 消电离层观测模型
本文分析的是双频的消电离层(IF)的伪距观测,其观测方程为[13]

式中:Pifj为基于载波频率fj(j=1,2) 的用户接收机到卫星i之间的伪距观测; ρi为接收机和卫星的天线相位中心之间的真实几何范围; dtr和 dti分别为接收机和卫星的时钟偏移;c为真空中光速;Ti为对流层延迟;bfj和Bfj分别为接收机和卫星的频率相关伪距硬件延迟; εi为观测噪声和未建模的残余误差.
在上述观测模型中,电离层延迟误差通过IF组合模型的方式来消除. 为提高SPP的定位精度, dti、dtr、bfj和Bfj项应完全消除,在此,利用IGS精密产品消除卫星位置和时钟误差,利用对流层模型修正对流层延迟误差. 而对于相对论效应、地球自转效应、地球固体潮和海洋潮汐引起的误差,若采用同样的方式对其修正,反而致使得到的定位结果精度不高,故在此SPP模型中可被忽略,不作考虑.
此外,卫星钟差项中集成了与卫星相关的硬件延迟,此由精确的卫星时钟误差乘积进行修正,同时与接收机相关的硬件延迟被整合到了接收机时钟误差项中,表示为[14]

式中: ζ 为卫星钟差 dti与卫星硬件延迟Bpj的整合误差; µ 为接收机钟差 dtr与接收机的硬件延迟bpj的整合误差. 当上述相关误差和噪声被忽略或校正后,式(1)可以写为

1.2 SPP参数估计
与传统的迭代算法不同,伪距观测方程的闭式解方法不需要迭代运算. 通过计算参考卫星和其他卫星伪距方程之间的线性无关差,则可将线性化应用于式(3).
假设有n颗(n≥5 )按仰角降序排列得可见卫星,则可以获得关于矩阵向量形式的未知参数(x,y,z,µ)的线性观测公式,记为

式中:r=[x,y,z]T;em=[1,1,···,1]T,m=n-1 ; ν 为 观测噪声;l=[ε1/δ1,ε2/δ2,···,εm/δm]T
,且


式中, χi=[αi/δi,βi/δi,γi/δi] ,i=1,2,···,n-1 ,有[15]为后续应用滚动时域估计算法,采用正交变换的方法来消除式(4)中的接收机时钟误差项µ.假定P∈Rm×m是正交变换矩阵,则有0,···,0)T. 根据householder 变换矩阵的定义,并通过相应代数计算,矩阵P可以具体表示为

为消除接收机时钟偏移参数 µ ,将式中的转换矩阵P代入式(4),可以获得初始正交变换为
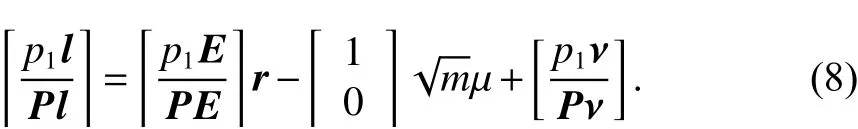
特别注意,由于只有第一个等式包含时钟偏移项µ,故余下的部分可写为

由此,模型的观测方程可表述为

式中:y为观测向量;H为向量r对应设计矩阵; ε 为误差修正项.
因此,可以使用上述线性方程直接求解接收机位置参数解,该方程不包括接收机时钟偏移项 µ .
为求解式(10)中的未知参数r,可以采用一般LS. 同时基于LS估计是以下最小化问题的解决方案,可表示为[16]

■■■■■■■

2 高度约束型MHE算法
2.1 高度约束
在假设先验高度信息没有误差的情况下,具有非线性等式的高度约束方程可表示为

式中:D=diag[1/(a+h),1/(a+h),1/(b+h)] ,a、b分别为WGS-84参考椭球的长半轴和短半轴;h为相对于WGS-84参考椭球的高度[17].
2.2 滚动时域估计
MHE算法按所用信息量的不同可分为全信息MHE和近似MHE. 全信息MHE方法利用了当前和过去时刻的所有测量数据,测量结果更为准确,但另一方面会造成“滚雪球”效应,导致问题不可解;近似MHE方法则是为了避免上述问题的出现,通过限制问题的维数,确保了求解的可行性.
2.3 附加高度约束的滚动时域估计
在实际应用中,有很多的状态方程都可以用来模拟接收机的状态模型. 本文使用如下状态方程来模拟接收机的状态模型:


式中:T为连续两个历元的时间间隔;系统噪声Q为:

式中:qx、qy、qz分别为不同分量上的过程噪声的功率谱密度;为使观测方程式(10)中的状态向量rk与过程方程式(14)中的状态向量Xk相同,将矩阵修改为包含有3个零列,如下所示:
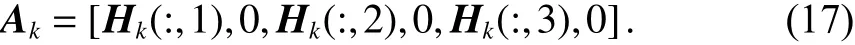
因此,所得SPP观测方程表示为

式中,R为观测噪声. 同理,将高度约束方程的相关矩阵D补充相应零列修改为

相应地,高度约束方程则可表示为

因此,高度约束MHE状态估计问题的目标函数构造如下:
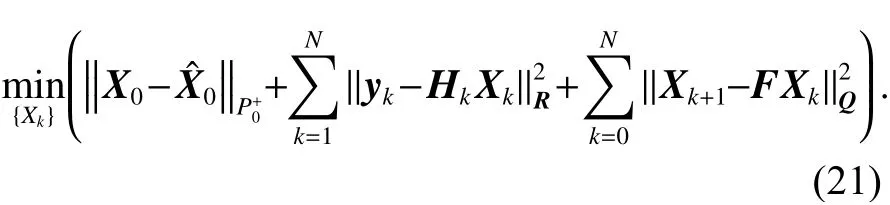
满足约束

为限制优化问题的维数,引入了长度为J的固定时域(J=N-M+1 ),将全信息估计问题的计算划分为两部分:{1 ≤k≤M-1 } 和{M≤k≤N},采用近似MHE算法将状态估计问题转为如下约束优化问题的目标函数
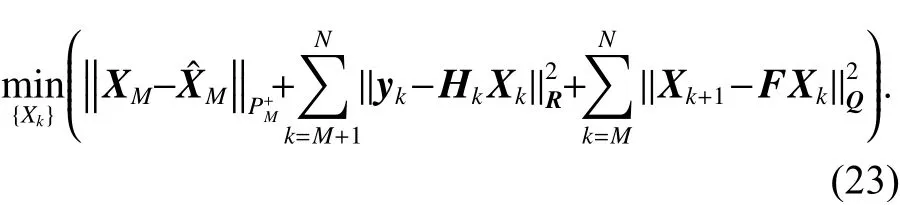
满足约束

式中: {Xk} 为 {XM,...,XN} ;N-M+1 为 滚 动 时域窗口长度;其维度为为后验估计协方差矩阵.
3 实验结果与分析
为评估MHE算法在高度约束SPP的性能,下面分别进行了静态实验和动态实验.
3.1 静态实验
本静态实验是基于AREG观测站(站点位置:阿雷基帕,经度为-71.492 9°,纬度为-16.465 4°,海拔高度为2 489.336 m)根据IGS提供的24 h GNSS观测数据,并以静态接收机的真实高度作为先验高度值,在MATLAB平台上进行了SPP定位实验. 实验方案如下:
1)无约束LS的SPP实验;
2)视窗长度为2 h,高度约束MHE的SPP实验(MHE-2);
3)视窗长度为4 h,高度约束MHE的SPP实验(MHE-4).
表1分别计算出了不同方案下SPP定位估计过程中的处理时长. 时间跨度是由MATLAB中的tic和toc函数计算,其中tic功能自动记录启动时间,toc计算程序运行时的时间差,可见相对LS算法,MHE算法的处理时间较长,且随MHE视窗大小的增加,程序运行时间也会急剧增加.

表1 不同方案的处理时长 s
图1为SPP在WGS-84直角坐标系下的定位估计误差. 利用接收机参考坐标与估计坐标之间的差值来计算误差值. 考虑到MHE计算量较大,所以图1分别给出了WGS-84直角坐标系下LS方法和前300个历元的MHE方法的SPP的估计误差结果. 可以看出,LS定位误差波动起伏较大,结果粗糙杂乱;而附加高度约束的MHE方案抗扰动性能更强,定位结果更为平滑,明显优于传统无约束LS方案的定位结果.

图1 三种方案在X、Y、Z方向上的定位误差比较
结合表2,与LS方案相比,MHE-2方案在X、Y、Z三个方向分量上的均方根(RMS)值分别从1.11 m、3.23 m、1.01 m降低到0.21 m、0.91 m、0.23 m,整体定位精度提高了73.03%;同样,MHE-4方案的RMS值分别降低到0.20 m、0.87 m、0.26 m,整体定位精度提高了81.46%.
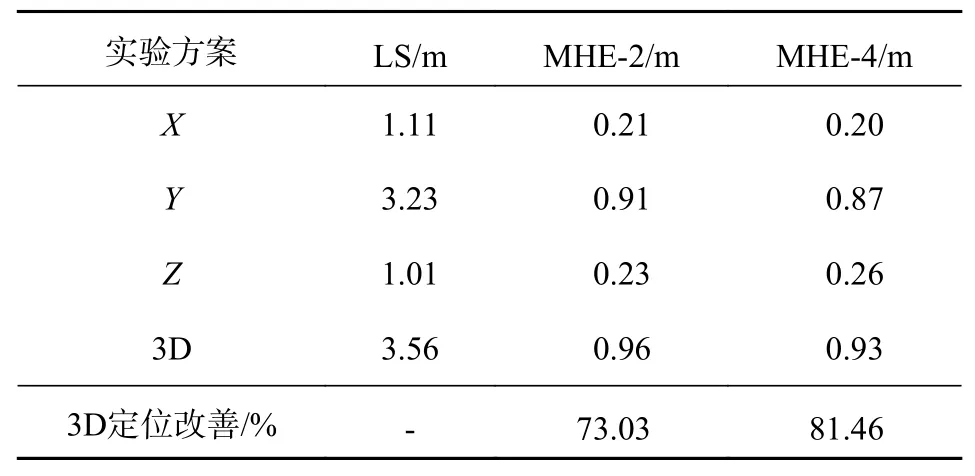
表2 SPP定位误差RMS值
3.2 动态实验
为了进一步评估附加高度约束MHE的SPP定位性能,通过实时采集的动态GPS卫星观测数据进行了动态SPP定位实验.
如图2所示本实验数据于2021年6月2日采集于武汉的中国科学院测量与地球物理研究所导航楼顶,从GPS时间(CPST)的10:37:00开始,观测时长约5 min. 实验过程中的动态接收机沿着自身圆形轨道匀速转动. 此外,在距离该数据采集地点约4.5 m的地方设有一个基准站(精确坐标已知)同时进行观测获取卫星观测数据,然后用RTKLIB软件的载波相位差模式进行解算动态接收机的位置坐标,以获得接收机的精确定位数据. 图3为实验中动态接收机的运动轨迹坐标.

图2 动态数据收集站点

图3 动态接收机运动轨迹
本次动态实验中,先验高度值被设置为所有历元的接收机定位的平均高度. 为了与静态实验相一致,并且较小视窗尺寸的MHE方法的定位精度的提高对实际应用也更有意义,因此,实验中MHE的视窗尺寸也设置为2和4.
图4为动态接收机做匀速圆周运动时,LS方法和前300个历元的MHE方法的SPP定位误差结果. 结果表明:与无约束LS相比,MHE两种方案的结果具有较小的波动,且MHE-4方案的结果优于MHE-2方案. 同时也不难发现,随时间推移,动态接收站工作趋于稳定及MHE-4方案观测数据信息的增加,其定位结果在250 s后相较与LS和MHE-2结果存在明显偏离,定位结果更为精确.

图4 三种方案在X、Y、Z方向上的定位误差比较
表3给出了前300个历元SPP定位的RMS误差. 由表3可知,与LS方案相比,MHE-2方案在X、Y、Z三个方向分量上的RMS值分别从3.81 m、7.31 m、4.14 m降低到2.53 m、4.70 m、3.11 m,整体定位精度提高了33.0%; MHE-4方案的RMS值分别降低到1.95 m、3.23 m、2.26 m,整体定位精度提高了52.4%.与MHE-2方案相比,MHE-4方案的整体定位精度提高了19.4%.
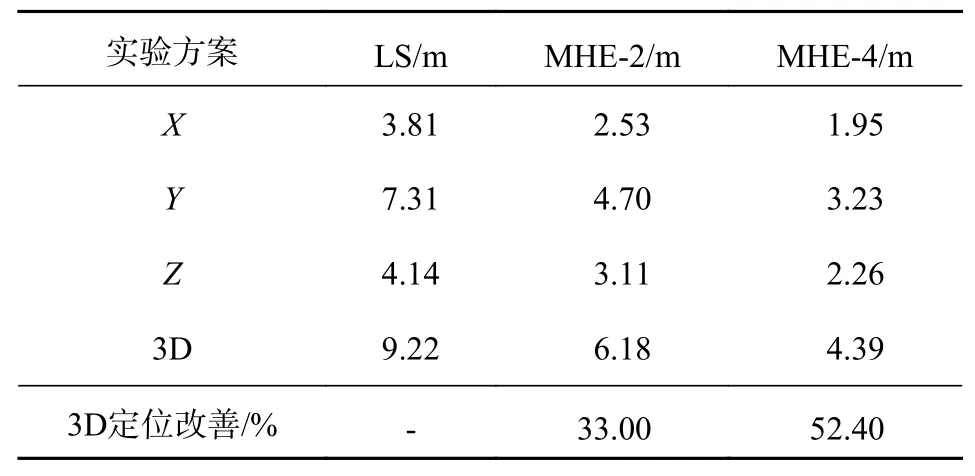
表3 SPP定位误差RMS值
4 结 论
SPP技术是一项重要的定位技术,可为一些特定的应用场景提供高鲁棒性的定位. 本文从国内外研究的先验信息可以用来增强单点定位性能的基础上,提出了附加高度约束的MHE算法来进一步提高SPP定位精度,并进行了静态和动态实验分析. 结果表明:相对于传统的LS方法,附加高度约束的MHE算法的单点定位结果更加准确和平滑,验证了该方法的有效性、可行性,可适用于更为广泛的应用场景.
但同时MHE算法的估计精度与运行效率互相矛盾,两者不可兼得,其中运行效率主要与视窗的大小有关. 在实际应用过程中,需要根据应用场景的不同,在定位估计精度和计算工作量之间折衷考虑视窗参数大小.
