北斗三号全球卫星导航系统空间信号精度评估

刘东亮，成芳，沈朋礼，李艳红，李晓婉

( 1. 中国科学院国家授时中心, 西安 710600；2. 中国科学院精密导航定位与定时技术重点实验室, 西安 710600；3. 中国科学院大学, 北京 100049 )

0 引 言

北斗三号(BDS-3)是我国卫星导航系统建设的第三步[1]，于2020年7月31号宣布正式开通，由24颗中圆地球轨道(MEO)卫星、3颗地球静止轨道(GEO)卫星和3颗倾斜地球同步轨道(IGSO)卫星组成. 相比北斗二号(BDS-2)卫星区域服务系统，BDS-3采用了全新的技术[2]，目标是为全球用户提供全天候、高精度的定位、导航和授时(PNT)服务，此外还提供区域短报文通信、全球短报文通信、星基增强、国际搜救、精密单点定位(PPP)等服务[3].

对于全球卫星导航系统(GNSS)，空间信号精度影响其服务性能. 大多数GNSS用户，在计算定位结果之前，需要获取广播星历中卫星轨道和卫星时钟信息，然而广播星历预测的轨道、时钟信息与实际值之间总是存在偏差，称为空间信号(SIS)误差. SIS误差沿用户视线的投影，即空间信号测距误差(SISRE)，是评估空间信号精度的关键指标. 目前已有部分学者对BDS-3的空间信号精度情况做了研究，文献[4-15]利用BDS-3部分卫星对BDS-3的空间信号精度进行短期的评估. 文献[16-17]选择2019年全年的数据，利用18颗MEO卫星对BDS-3的空间信号精度进行了评估. 文献[18]选择2019—2020年 2 a的数据，利用18颗MEO对BDS-3的空间信号精度进行评估.文献[16-18]评估时间跨度长，但仅利用了BDS-3的少量卫星来对BDS-3的空间信号精度进行了评估.文献[19]选择2020-03-29—05-02的数据，分别利用德国波茨坦地学研究中心(GFZ)、武汉大学IGS数据中心(WHU)和上海天文台(SHA)三家分析中心提供的精密轨道和钟差进行了对比评估，但存在评估时间短的局限. 随着BDS-3的30颗卫星实现星间链路，完成星座组网，以上研究结论已不具备时效性.

针对BDS-3正式开通之后的空间信号精度情况，本文选取2020-08-01—2021-07-31共1 a的混合广播星历数据，以GFZ和WHU提供的精密星历为参考从广播星历轨道精度、钟差精度和SISRE 对BDS-3的空间信号精度情况进行了全面的比较分析.

1 评估分析方法

广播星历因其具有的实时性和易获取性，在导航定位中广泛使用，故可以通过对广播星历的分析来对BDS-3空间信号精度进行评估，过程分为轨道精度评估、钟差精度评估、SISRE评估三部分. 评估时需要选择参考基准，精密星历精度高于广播星历1～2个数量级，因此可以作为参考基准. 本文选择GFZ和WHU的精密星历作为参考，从卫星轨道精度、钟差精度、SISRE方面来对BDS-3的空间信号精度情况进行评估. 表1给出了文中所使用的精密星历信息. 关于BDS-3卫星的轨道类型、星载原子钟、制造商信息和运行状态如表2所示，可以看到C61卫星正在测试阶段，而其他BDS-3卫星投入使用，因此本文只关注剩下的29颗BDS-3卫星.

表1 BDS-3精密星历信息

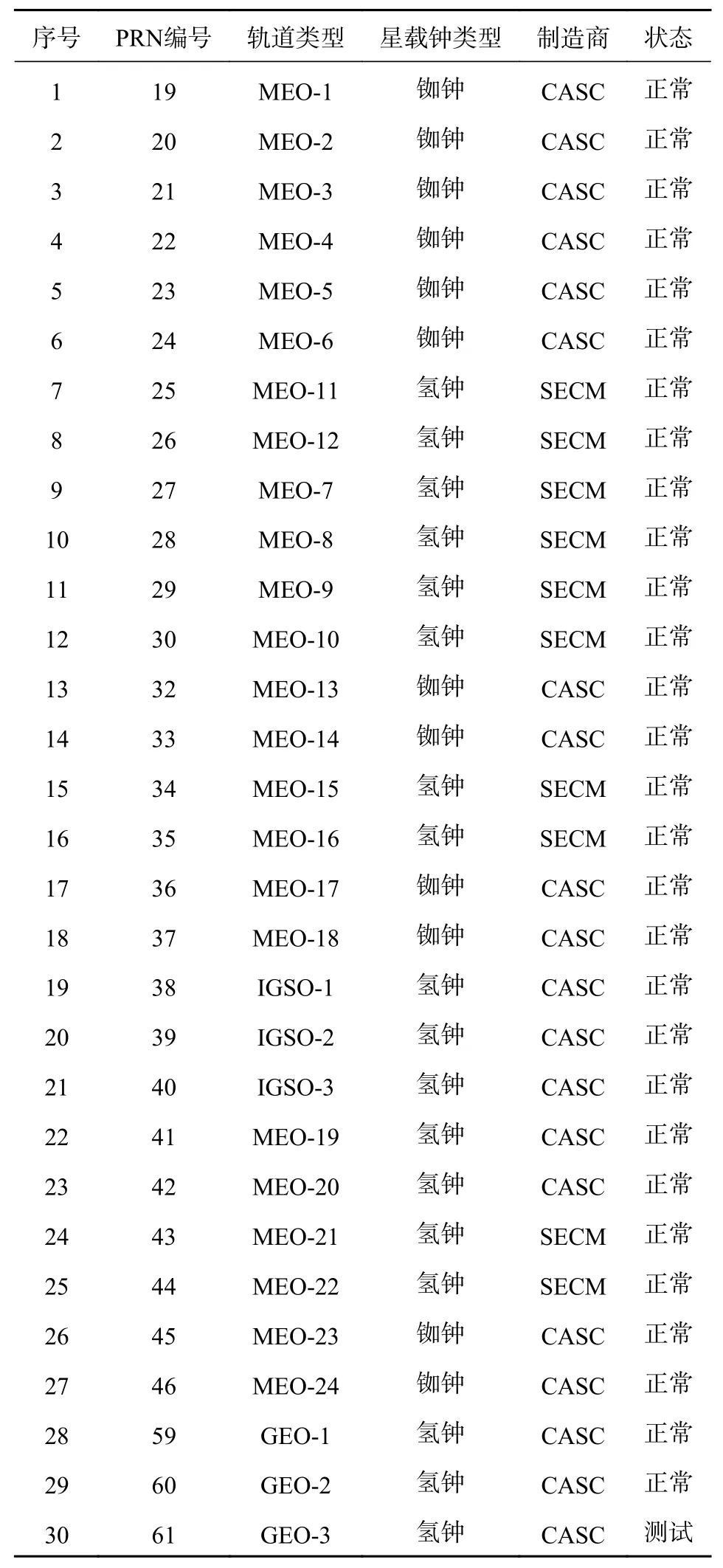
表2 BDS-3卫星轨道、星载钟、制造商和运行状态汇总

1.1 轨道精度评估

轨道精度的评估可采用激光测距(SLR)[20]数据和后处理精密轨道产品，本文选择后者进行研究. 将广播星历计算的卫星位置和精密星历提供的卫星位置作差从而求出卫星的三维轨道差，最后将其转换至轨道坐标系，轨道误差通常用径向(R)误差、切向(A)误差、法向(C)误差三个分量来表示，转换公式如下：

式中：Xsat为 卫星质心位置矢量；Vsat为卫星速度矢量；×为 叉乘；eR、eA、ec分 别为轨道R、A、C单位矢量； dx、dy、 dz分别为广播星历和精密星历提供的卫星位置之差；ΔR、ΔA、ΔC分别为广播星历轨道R、A、C误差. 卫星轨道精度分析方法如图1所示. 在轨道精度分析中需要注意以下两个问题.

图1 轨道精度分析流程图

1) 参考框架不一致. 广播星历采用的是北斗坐标系(BDCS)，BDCS的定义和中国大地坐标系(CGCS)[21]一致，各个分析中心提供的精密星历基于ITRF2014[22]框架，参考框架不一致，应采用7参数转换[23]至同一坐标系进行比较，由于BDCS和ITRF2014的差异仅为2～3 cm[21]，相比广播星历米级的精度可忽略不计，因此本文不考虑BDCS和ITRF的坐标转换.

2) 卫星位置参考点不一致. 广播星历计算的卫星位置基于卫星天线相位中心，而精密星历计算的卫星位置基于卫星质心，两者之间存在偏差，在比较前需统一到卫星质心或者天线相位中心，考虑到天线相位中心偏差(PCO)在数值上为米级，而天线相位中心变化(PCV)为毫米级，故只考虑PCO修正. 假定PCO在星固坐标系中的坐标为(x,y,z)，则转换到地心坐标系中的偏差量[24]表示为

用r表示地心卫星矢量，rs表示地心太阳矢量，ex、ey、ez的计算方式[24]如下：

中国卫星导航系统管理办公室测试评估研究中心 (TARC-CSNO)公布了卫星制造商地面标定的北斗PCO模型[25]，其发布的PCO模型未包含C60卫星，IGS官网公布的BDS-3的PCO模型也是由TARCCSNO提供，故C60卫星的PCO参数暂且采用天线文件igs14_2163.atx[26]，本文采用B3频点的PCO统一到卫星天线相位中心来进行比较.

1.2 钟差精度评估

根据采用钟差基准类型的不同，广播星历钟差评估方法分为观测量比较法[27]和精密钟差比较法两种，本文采用后者进行分析. 卫星钟差精度分析流程如图2所示，钟差精度分析时需要注意以下几个问题.

图2 钟差精度分析流程图

1) 卫星钟差的参考频率不一致. 广播星历钟差的频率基准为B3I频点，由于BDS-3不支持B2I信号且目前正处于BDS-2向BDS-3过渡的阶段，故包含BDS-2/BDS-3的精密产品均采用B1I/B3I消电离层组合[28-29]. 在比较前需进行群延迟(TGD)修正，修正公式为

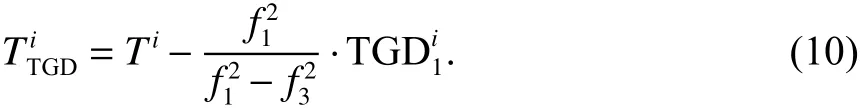
式中：Ti为第i颗卫星的广播星历钟差；f1、f3分别为B1I和B3I信号的频率；为 第i颗卫星B1I和B3I之间的群延迟参数，对应广播轨道6的第三个参数；表示TGD修正后的第i颗卫星的广播星历钟差.

2) 卫星天线相位模型不一致. 在精密定轨中PCO(主要是z分量)大部分会被卫星钟差吸收[30]，不同机构采用的PCO模型可能存在差异，故当选择卫星质心作为参考时，需要消除两者定轨时采用的PCO模型不一致引起的偏差. 本文选择卫星天线相位中心作为参考，故不考虑此项修正.

3) 时间基准不统一. 广播星历钟差和精密星历钟差具有不同的时间基准参考，在钟差比较时会导致偏差，其特点是对星座中所有卫星都有影响，并作为一种系统差随时间变化. 因此不能通过广播钟差和精密钟差做一次差来评估广播钟差精度. 需要消除由于参考钟的选取不同引起的偏差值，可以利用全星座所有卫星广播星历与精密星历钟差之差的均值来进行此系统误差的修正，公式[11]表示为：

1.3 SISRE评估

SISRE为卫星在地球表面覆盖范围内的所有点瞬时SISRE的均方根(RMS)统计值，给出SISRE的表达式为[31]

如果忽略钟差误差T，则得到仅受轨道影响的空间信号测距误差SISRE[32]，表达式为

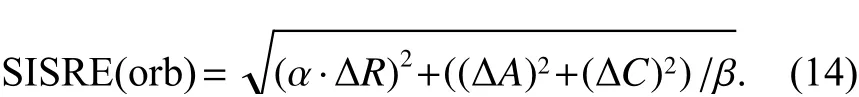
式中，c为光速. α 和 β 的取值[33]如表3所示.

α β表 3 北斗卫星导航系统 和 的取值

2 数据预处理

在进行评估前需要进行数据预处理，具体如下：

1) 精密星历缺失或精密钟差为999 999.999 999(精密钟差数据错误)时不进行评估；

2) 剔除广播星历健康标志为1的不健康星历数据；

3) 选取广播星历时间间隔最近的星历数据进行广播位置和钟差的计算，即 |tk-toc| 最 小，tk为计算位置时刻，toc为广播星历中的钟差参考时刻；

4) 评估所使用的大量数据可能存在粗差，本文将计算结果中大于3倍中误差的钟差误差和轨道误差作为粗差剔除.

3 结果与分析

3.1 轨道精度分析

图3表示了以GFZ和WHU精密轨道为参考，每颗卫星各天R、A、C方向广播星历轨道误差的RMS误差统计结果，由图3分析可得：

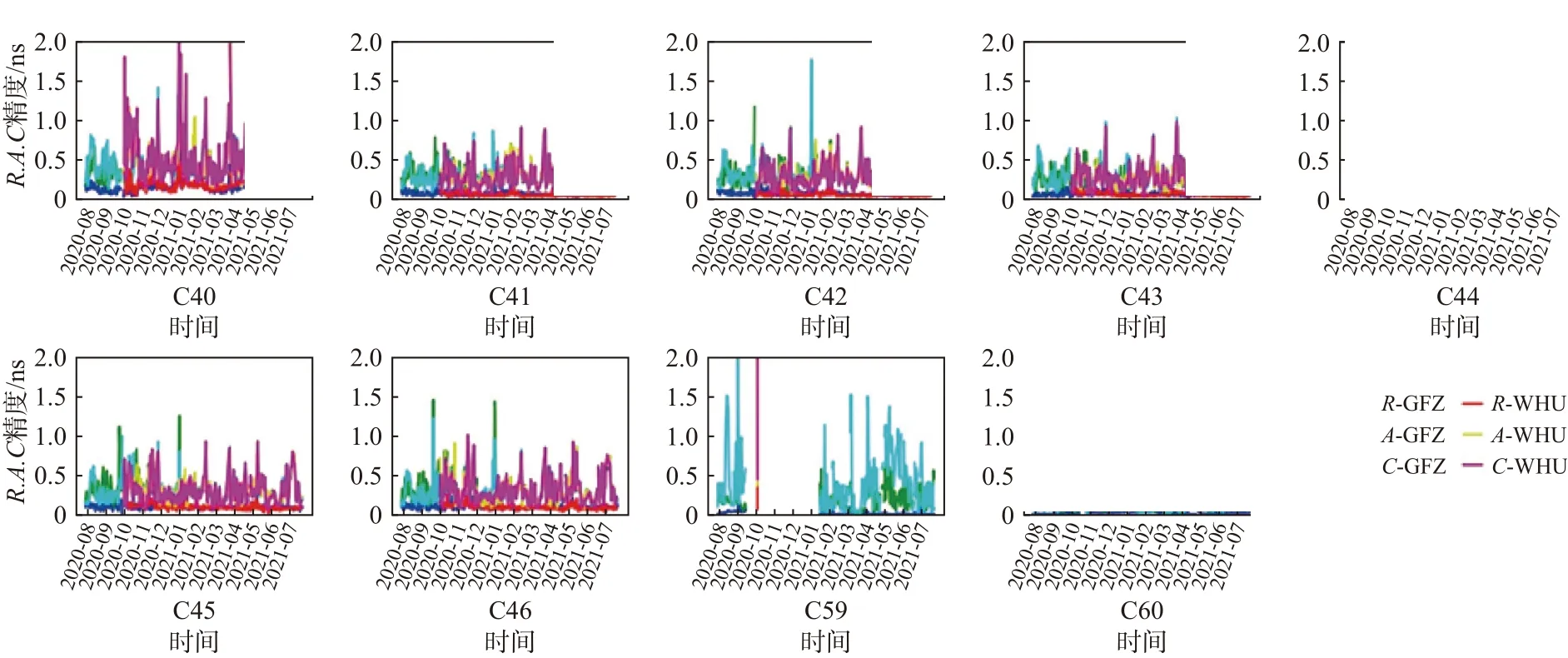
图3 BDS-3广播星历卫星轨道误差变化图

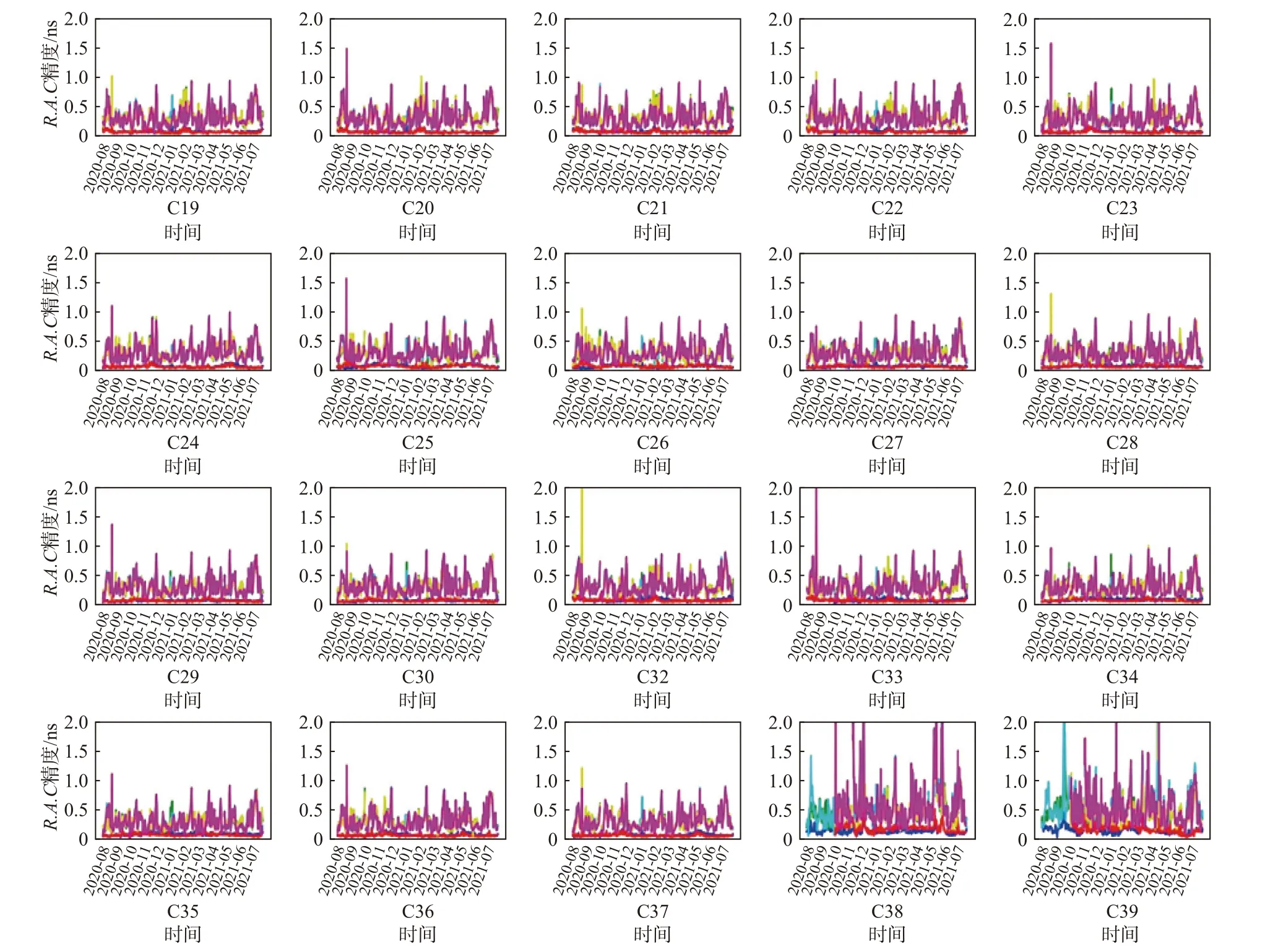
1)以GFZ和WHU精密轨道为参考分析的广播轨道误差具有较高的统一性，广播轨道误差在R方向上基本小于0.5 m. WHU在2020年10月后开始提供C38～C46卫星的精密轨道信息，不提供C60卫星的精密轨道信息. 广播轨道误差每隔一段时间会出现误差较大的情况，可能是卫星机动[34]和星蚀期影响所致.

2) GEO卫星的广播轨道误差随时间变化很大，尤其是A、C方向的广播轨道误差变化波动很大，可能是GEO卫星观测站点有限、几何结构较差[35]、卫星基本处于静止状态，测站对A、C不敏感所致. IGSO卫星的广播轨道误差较大，可能是高轨、星下点为“8”字形导致站星几何结构变化不明显所致. MEO卫星的广播轨道误差变化最小.

以WHU精密轨道为参考时，通过计算发现C59卫星只在2020年10月5日、10月6日、10月7日有广播轨道误差信息，10月5日和10月6日统计的广播轨道误差在R、A、C方向上均大于100 m，10月7日的广播轨道误差在R、A、C方向上分别小于0.1 m、3 m、4 m，C59卫星广播轨道误差信息极少不可用于广播轨道精度的统计，故暂不做考虑. 通过计算365天广播轨道RMS误差的平均值来获得广播轨道精度情况，图4中以GFZ和WHU精密轨道为参考分析的卫星广播轨道精度基本一致.

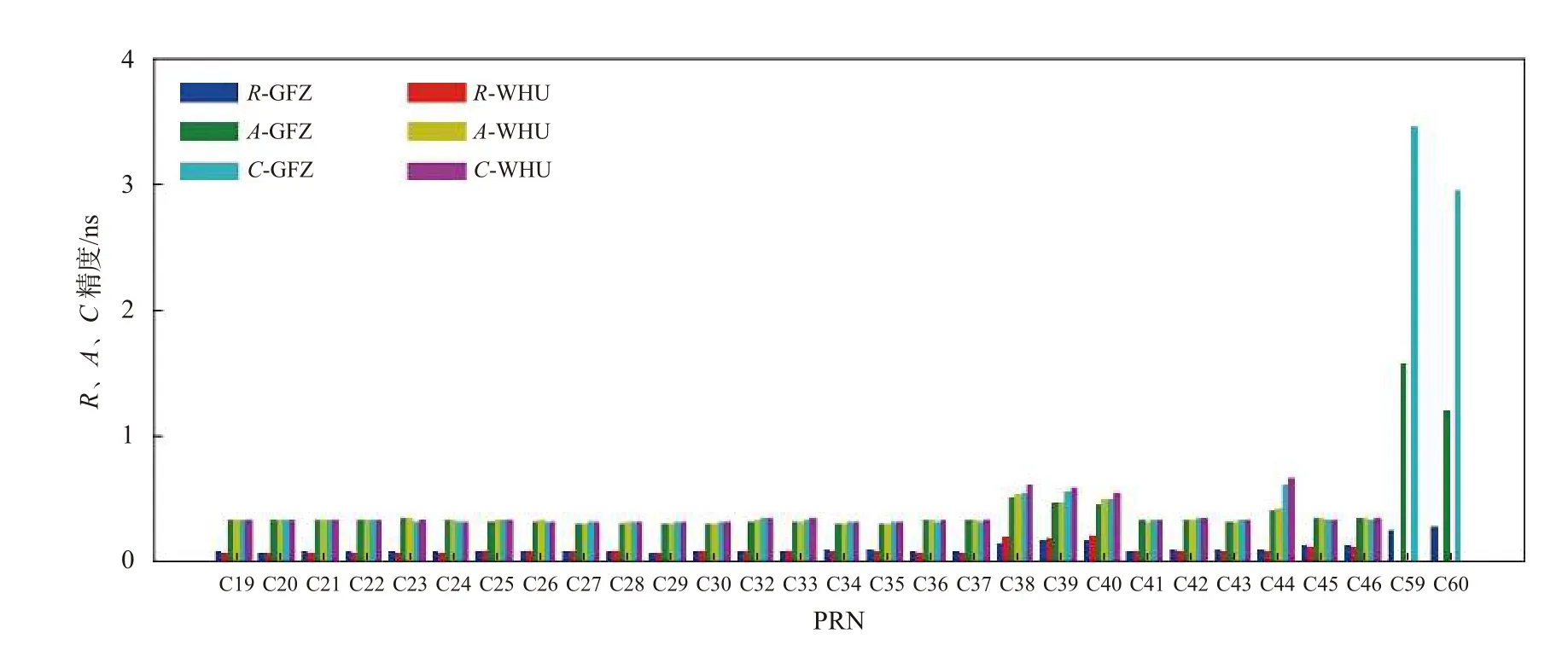
图4 BDS-3广播星历卫星轨道精度统计图

3.2 钟差精度分析

图5中以GFZ和WHU精密钟差为参考，每颗卫星各天广播钟差误差的RMS误差统计结果. 由图5分析可得：

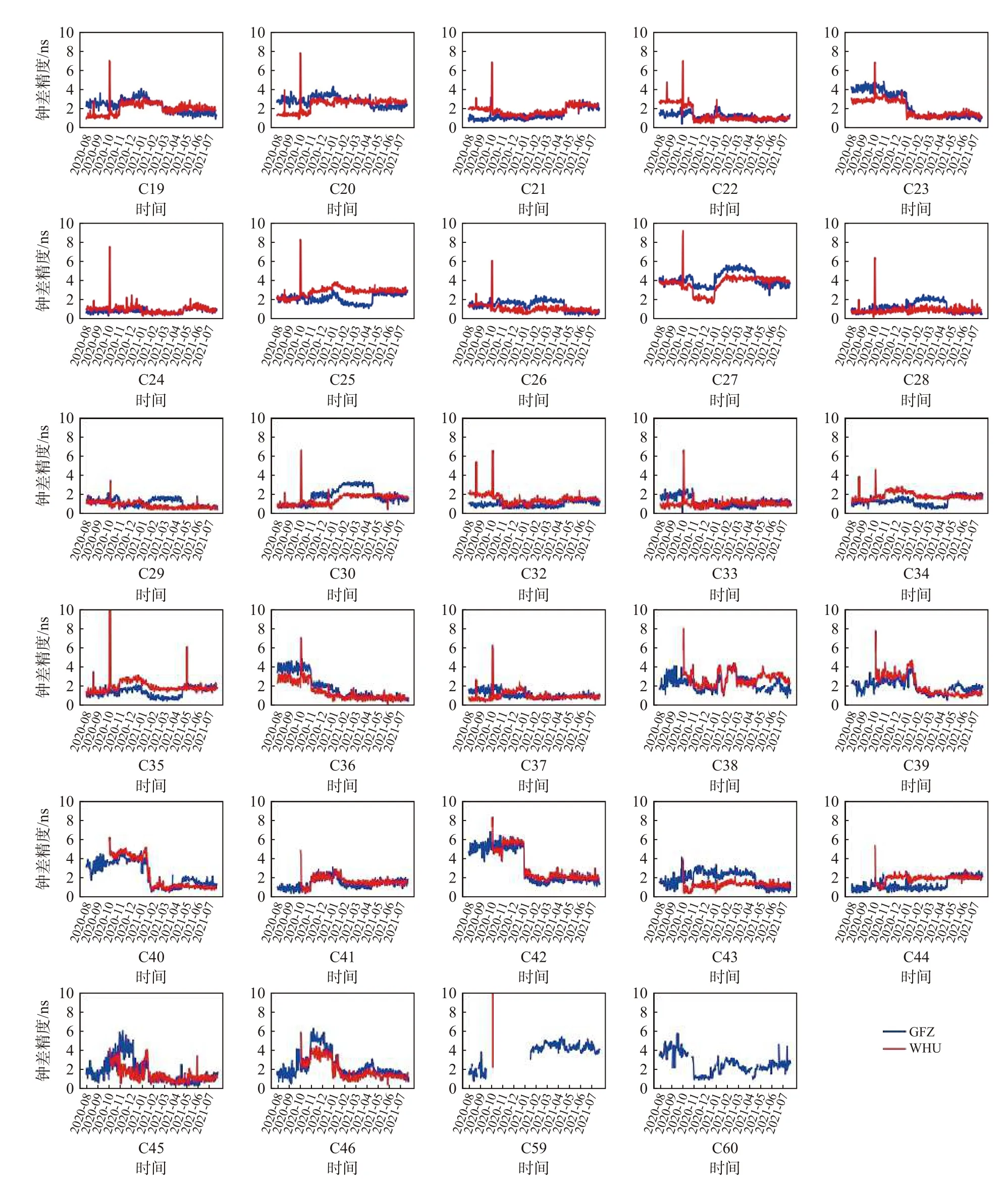
图5 BDS-3广播星历卫星钟差误差变化图

1)以GFZ和WHU精密钟差为参考分析的广播钟差误差变化规律基本保持一致，广播钟差误差基本小于10 ns. WHU在2020年10月开始提供C38～C46卫星的精密钟差信息，不提供C60卫星的精密钟差信息. 当选择WHU精密钟差为参考时，发现所有卫星的广播钟差误差在2020年10月5日和10月6日明显变大. 同时我们看到C59卫星的广播钟差误差在10月5日和10月6日的钟差误差均大于100 ns，10月7日的钟差误差小于3.5 ns，全年数据极少可靠性低故不用于广播钟差精度的统计，故在后面广播钟差精度的统计中不做考虑.

2)对于MEO卫星，以GFZ和WHU精密钟差为参考统计的广播钟差误差在2021年5月之后统一性较高. 对于BDS-3不同轨道卫星，MEO卫星的广播钟差误差变化最小，其次是IGSO卫星，MEO卫星的变化最大.

以WHU精密钟差为参考时，通过计算365天广播钟差RMS误差的平均值来获得广播钟差精度情况，图6中以GFZ和WHU精密钟差为参考分析的卫星广播钟差误差一致性相比轨道误差较低，可能是两家机构精确时钟偏差的处理策略不同所致. 对于C59卫星，当采用WHU精密钟差为参考时，前面已经讨论，不做统计评估.

图6 BDS-3广播星历卫星钟差精度统计图

3.3 SISRE分析

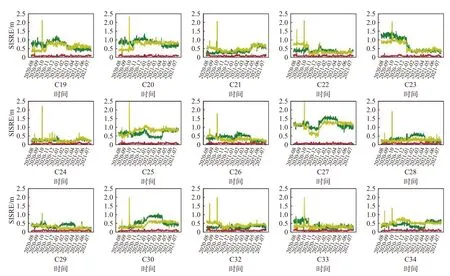
图7表示了以GFZ和WHU精密星历为参考，每颗卫星每天SISRE(orb)、SISRE的均值统计结果.由图7可知以GFZ和WHU精密星历为参考统计的SISRE(orb)变化规律和结果具有高度的统一性，对于SISRE，考虑了钟差误差的影响，得出的变化规律一致性较差. 图8统计了365天SISRE(orb)、SISRE的均值情况，对于SISRE(orb)，GEO卫星的最大，其次是IGSO卫星，MEO卫星的最小. 而对于SISRE，受钟差误差的制约导致几颗MEO卫星的SISRE大于IGSO卫星. 由图7～8可知BDS-3卫星SISRE(orb)远小于SISRE，故钟差精度是制约空间信号精度的关键因素.

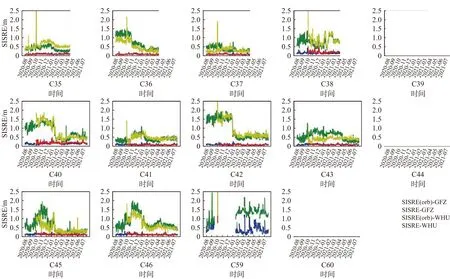
图7 BDS-3卫星 SISRE(orb)、SISRE变化图

图8 BDS-3 卫星SISRE(orb)、SISRE统计图

不同分析中心在姿态模型、太阳光压模型及精确钟差估算过程中参考站选择等方面可能采用不同的求解策略，所以精密产品记录的数据量和数据质量可能存在差异，从而用于卫星轨道和钟差误差计算的有效数据量(经过数据预处理之后的卫星数据量)不同，有效数据量越大统计的结果更具可靠性. 本文用卫星数据有效率(卫星有效数据量与不存在数据缺失的理想数据量的比值)来衡量卫星有效数据量的大小，卫星数据有效率越大说明卫星有效数据量越大，得出的结果也更加可靠. 图9给出以GFZ和WHU精密星历为参考BDS-3卫星数据有效率的统计情况， 由图9可知对于C19～C30、C32～C37卫星，采用GFZ和WHU精密星历的卫星数据有效率基本一样，但对于其他卫星，采用GFZ精密星历统计的卫星数据有效率明显比WHU高，尤其是C59、C60卫星，C59卫星采用WHU精密星历为基准时卫星数据有效率几乎为0，C60 卫星数据有效率则为0.

综合前面选择GFZ和WHU精密星历为参考对卫星轨道精度、钟差精度及SISRE的分析，发现基于两家分析中心评估的结果具有较高的一致性. 由图9可知采用GFZ精密星历时可用于统计分析的卫星数据量明显高于WHU，因此本文给出以GFZ精密星历为评估基准对BDS-3空间信号精度的具体统计情况. 表4统计了BDS-3的钟差精度、轨道精度、SISRE(orb)和SISRE，由表4可知对于MEO卫星，除C45和C46卫星R向精度高于0.1 m之外，其他卫星的R向精度均优于0.1 m，C27、C42卫星的钟差精度较差；对于IGSO卫星，C39卫星的空间信号精度明显高于C38、C40卫星；对于GEO卫星，C59卫星的空间信号精度较差，SISRE为1.295 m， C60卫星的SISRE相比C59卫星减少0.316 m.

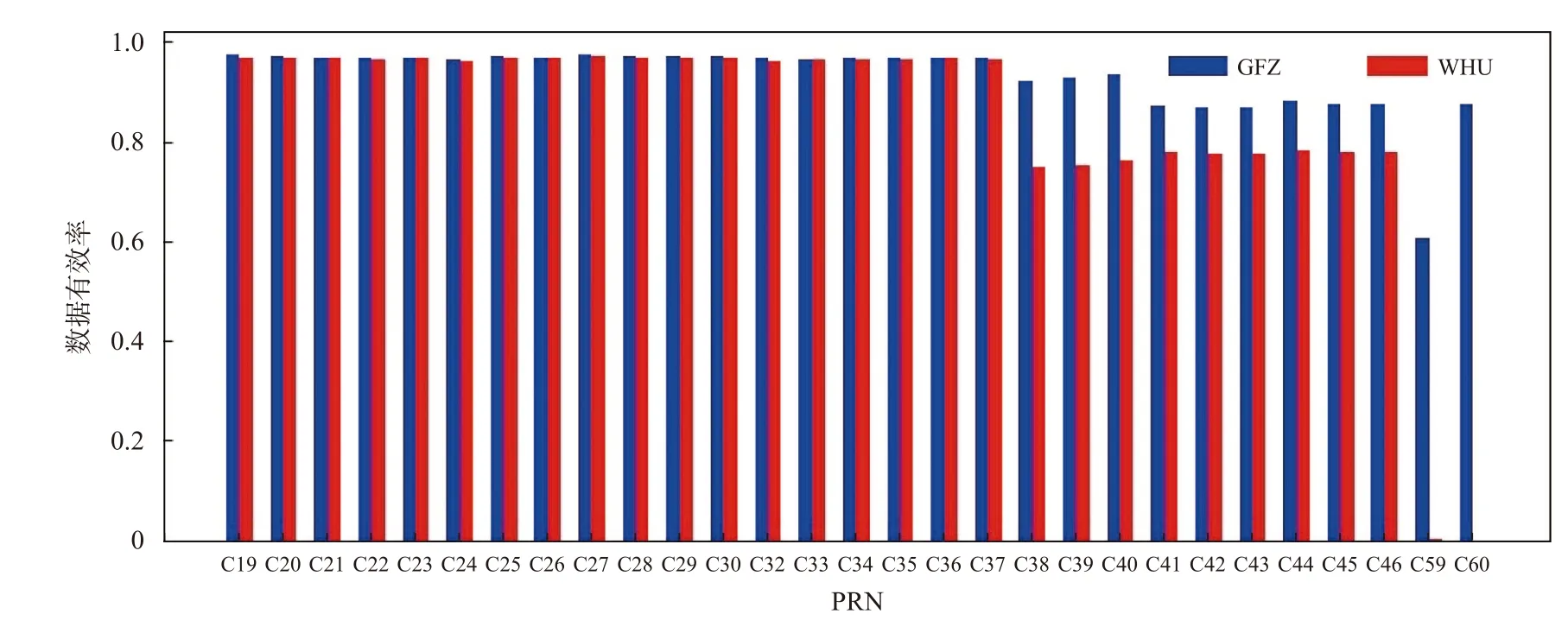
图9 BDS-3卫星数据有效率对比图

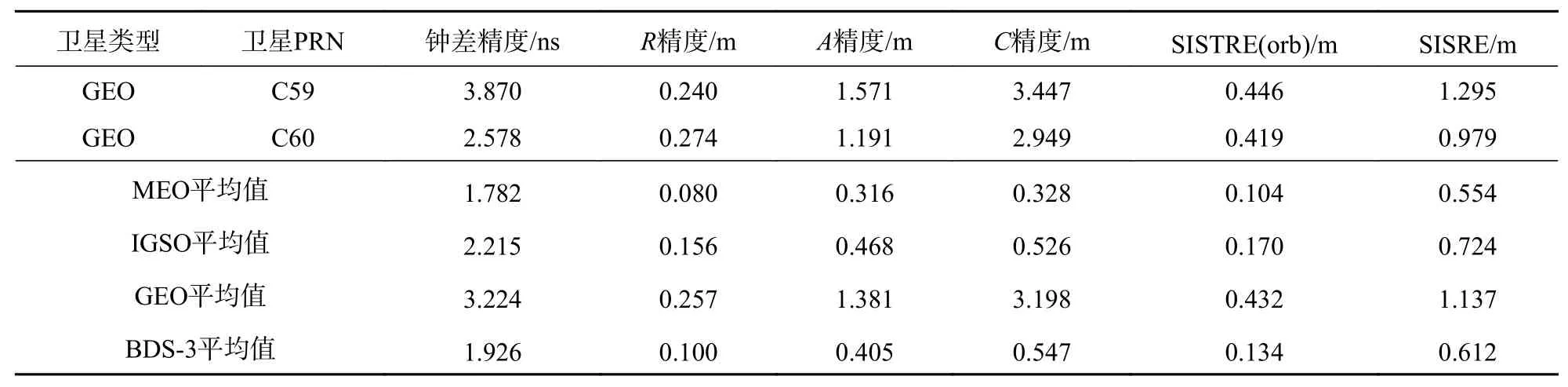
表4（续）

4 结束语

基于BDS-3正式开通一年间的数据，以GFZ和WHU的精密星历作为参考，对BDS-3广播轨道精度、广播钟差精度、SISRE进行了比较分析，在考虑了卫星数据有效率的情况下统计了以GFZ精密星历作为评估基准的BDS-3空间信号精度情况. 结果表明：

BDS-3的轨道精度在R、A、C方向上分别达到0.100 m、0.405 m、0.547 m，钟差精度达到1.926 ns，SISRE(orb)为0.134 m，SISRE为0.612 m. 在三种轨道类型中，MEO卫星的空间信号精度最好，其SISRE(orb)和SISRE统计值分别为0.104 m、0.554 m；IGSO卫星次之，SISRE(orb)和SISRE统计值分别为0.170 m、0.724 m；GEO卫星的空间信号精度最差，SISRE(orb)和SISRE统计值分别为0.432 m、1.137 m.IGSO和MEO卫星的SISRE相比GEO卫星分别减少36.3%、51.3%.

本文对BDS-3的29颗卫星进行了分析，不包含C61卫星(测试阶段)，随着C61卫星的运行和时间推移，BDS-3的空间信号精度需进一步分析.