顾及卫星姿态的多系统精密钟差产品综合

毛姝尹，魏娜，温强，闫哲

( 1. 武汉大学 卫星导航定位技术研究中心, 武汉 430079；2. 武汉大学 测绘学院, 武汉430079 )

0 引 言

随着GPS、GLONASS、Galileo和北斗卫星导航系统(BDS)四大全球卫星导航系统的全面发展与建设，多系统全球卫星导航系统(GNSS)已经成为高精度导航定位的基础. 而精密单点定位(PPP)技术[1]是多系统GNSS在广域内实现高精度定位的关键. 为方便用户实现PPP技术，国际GNSS服务(IGS)各分析中心提供了精密的卫星轨道、卫星钟差等产品. 随着多系统GNSS的繁荣发展，各分析中心于2012年陆续开始提供日常运行的多系统GNSS精密产品[2]，例如欧洲定轨研究中心(CODE)、德国地学研究中心(GFZ)和武汉大学(WHU)等[3-5]. 近年来，精密产品的种类也不断丰富，2018年，IGS提出各分析中心应发布与钟差产品配套的姿态产品[6]，使用户端和服务端的卫星姿态模型保持一致，从而进一步提高卫星在地影期的定位精度.

精密产品的精度直接决定了PPP的精度，单个分析中心提供的精密产品容易出现粗差或缺失等情况，因此IGS提出综合多家分析中心的产品以获得更加稳定可靠的精密产品[7-9]；与此同时，可以根据精密产品综合时的一致性评估各分析中心产品的精度.目前IGS日常仅对GPS的精密产品进行综合和评估，综合产品被广泛应用于各种高精度科学研究和实际应用中.

2011年，IGS开展MGEX (Multi-GNSS Experiment)，国内外陆续开展针对多系统精密产品综合的研究. Fritsche于2016年基于CODE、GFZ、TUM和WHU的产品实现了GPS、GLONASS、Galileo、BDS和准天顶卫星系统(QZSS)多系统精密轨道综合. 其中，Galileo和BDS 中圆地球轨道(MEO)卫星一致性可达到5 cm，BDS 倾斜地球同步轨道(IGSO)卫星和地球静止轨道(GEO)卫星一致性分别为0.1～0.2 m和1～2 m[10]. 陈康慷等[11]于2016年基于国际GNSS检测评估系统(iGMAS)钟差产品进行了GPS、Galileo、GLONASS和北斗二号(BDS-2)的多系统钟差综合实验，提出三步法基准对齐策略. 但文中尚未讨论多系统钟差综合的特殊性，对最终的综合钟差产品质量也未进行详细的分析.

1 顾及姿态的钟差产品综合原理

1.1 精密钟差按产品模型

精密卫星钟差是维持卫星导航定位系统时间基准的基础. 常利用无电离层组合的非差相位和伪距观测值，将卫星钟差、测站钟差、测站坐标和地球自转参数等一起估计. 估计得到的精密钟差并不是严格物理意义上的星载原子钟钟差，还包含估计过程中引入的误差. 精密卫星钟差的数学模型如下所示：

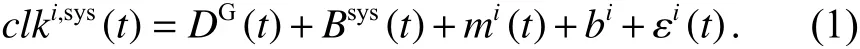
式中：i代表GNSS卫星； s ys 代表GNSS卫星系统；clki,sys(t) 为t时刻精密钟差产品中卫星i的钟差值；DG(t) 为t时刻GPS时(GPST)下的钟差基准. 由于卫星钟差和测站钟差相互耦合，无法同时估计，因此必须先固定某一基准钟(外接原子钟的测站)的钟差，再估计卫星的相对钟差，估计的精密钟差产品中将包含该基准钟差的影响.Bsys(t) 为GNSS系统的系统间偏差，包含其他卫星系统相对于GPS系统时的差异以及基准测站对于不同系统信号的硬件延迟差异；mi(t)为精密钟差产品估计中的模型误差，主要包括轨道误差和卫星姿态误差等；bi为初始钟偏差，包含伪距的测量误差和卫星端伪距硬件延迟的影响，是常量偏差； ε

i(t) 为相对钟差以及估计过程中的随机误差.

1.2 精密钟差综合算法

不同的分析中心估计精密钟差产品的原始数据和策略不统一，导致不同的钟差产品间存在系统性偏差，无法直接进行综合. 因此，在综合之前，需要将这些系统性差异从钟差产品中去除. 由于无法求得绝对的系统偏差，通常选取一个参考分析中心，将各分析中心的精密钟差产品与参考分析中心的产品做差，得到相对误差

在综合之前，需要对ΔDG(t)、ΔBsys(t)、Δmi(t)和Δbi等相对误差进行改正. 具体流程如下所示：

1) 模型误差改正

精密钟差产品在估计过程中会吸收轨道误差和卫星姿态误差. 考虑到各分析中心使用的卫星轨道和卫星姿态不一致的情况，需要在综合之前改正上述模型差异. 轨道误差改正如下所示[8]：

淼哥头也不抬、继续看书：“你中午是不是肥肉吃多了？脑袋被油糊短路了吧！游泳池里能怀孕？你怎么不说你从这里射了一箭，正好戳中非洲大草原一头奔跑着的狮子，它左耳朵上叮着的臭虫的右眼睛呢？”

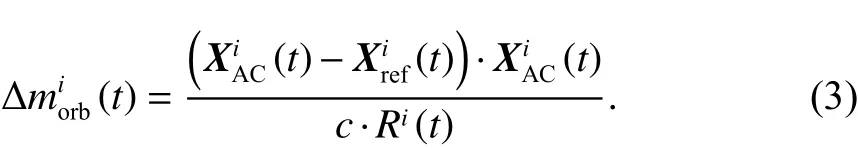
i(t) 为t时 刻 卫 星i与 地 心 的 距 离.除了改正卫星轨道的差异，还需要对卫星姿态差异进行改正. 卫星姿态主要影响钟差估计过程中的卫星天线相位偏差(PCO)改正和相位缠绕改正. 其中卫星天线始终指向地心，因此使用不同卫星姿态时，PCO的z轴分量在卫星至测站方向的投影始终不变，仅影响x轴和y轴分量在卫地方向的投影，量级不大，因此忽略其影响. 目前仅考虑卫星姿态对相位缠绕改正的影响[6].

2) 时间基准对齐

不同分析中心选取的基准站不同，会导致其精密钟差产品之间存在时间基准差异，同一系统所有卫星时间基准差异相同，因此针对多系统精密钟差产品，可以分系统对齐时间基准

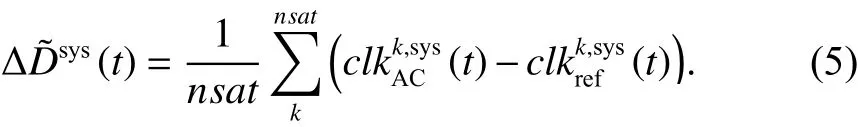
3) 初始钟偏差对齐

精密钟差估计时，高精度的载波相位观测值中由于包含模糊度，无法单独确定绝对的钟差. 一般利用低精度的伪距观测值确定钟差绝对值，载波相位观测值用于确定钟差的历元变化值. 由于伪距观测值精度低，其确定的钟差绝对值不够精确，容易受到观测值质量的影响. 因此分析中心使用的测站不同，观测质量存在差异时，会导致钟差产品之间存在系统性差异，该差异即为初始钟偏差差异，其改正如下所示：

4) 抗差综合

经过模型差异改正、钟差基准对齐和初始钟偏差对齐后的精密钟差产品即可进行综合. 综合过程中可利用钟差一致性剔除粗差. 主要采用绝对偏差中位数(MAD)作为统计指标进行粗差探测[14].

2 钟差综合实验

2.1 实验数据

本文使用IGS第三次重处理的产品进行多系统卫星钟差综合实验. 表1展示了综合使用的分析中心及其提供的卫星姿态产品情况，除欧洲航天局(ESA)外，其余四家分析中心均提供了姿态产品，该姿态产品即为分析中心计算钟差产品时使用的姿态. IGS也根据综合轨道计算了参考姿态. 其中，CODE姿态产品采样率为15 min，其余分析中心的产品采样率均为30 s. 综合过程中需要将各分析中心姿态与IGS参考姿态之间的差异改正至钟差产品中，最终生成与IGS参考姿态配套的IGS综合钟差. 因此需要对15 min采样的姿态产品进行球面内插使其与钟差产品采样率一致. 具体综合流程主要包括四步：首先对各分析中心的卫星钟差产品进行模型差异改正，包括径向轨道差异改正和姿态差异改正；其次选取各分析中心共有的卫星进行时间基准对齐；第三步对初始钟偏差进行分段对齐；最后对各分析中心产品进行迭代加权平均获得最终综合的钟差. 为了评估姿态改正对钟差综合的影响，本文共生成两套综合产品，分别为CMN和CMB. 其中CMN表示不改正分析中心间姿态差异的综合产品；CMB表示以IGS姿态为参考，改正姿态差异的综合产品.

表1 各分析中心卫星姿态产品情况

本文将对钟差综合残差，即各分析中心钟差产品与综合产品的差异进行分析，从而评估分析中心提供的多系统产品的精度和一致性. 同时，为了进一步验证综合钟差产品相对于单个分析中心产品的优势，分别使用综合钟差产品以及各分析中心产品进行PPP动态和静态解算. 实验时段为2020年第300～330天，实验测站为全球均匀分布的142个IGS测站，其分布如图1所示. 针对多系统GNSS静态定位，统计了31天的坐标重复精度；动态定位时，利用静态解作为参考真值，统计坐标序列的标准差(STD).

图1 PPP测站分布

2.2 综合实验

图2展示了2020年第300～330天GPS、Galileo和GLONASS改正姿态差异后的综合残差的均方根(RMS)，表2中为对应的31天RMS统计结果. 可以发现，各分析中心GPS和Galileo的钟差一致性较好，除了个别天少数卫星的RMS值达到30 ps，89.4%的GPS和95.5%的Galileo综合残差的RMS值均小于10 ps，31天的RMS平均值分别为8.0 ps和7.3 ps.各分析中心GLONASS钟差的一致性最差，仅有43.6%的综合残差小于30 ps，RMS最大可达到113 ps，31天的RMS统计值为47.3 ps. GLONASS钟差一致性较差是由于其轨道精度较低，分析中心间轨道差异大. 由于钟差综合过程中仅改正了轨道的径向差异，轨道切向和法向差异依旧会影响钟差一致性[15]. 图3展示了分析中心轨道与IGS综合轨道的切向和法向差异的RMS(简称为横向轨道差异). 可以发现横向轨道差异与综合钟差残差有明显的对应关系. 部分GLONASS卫星轨道横向差异长期接近甚至超过50 mm，例如R01、R13和R16等, 其钟差综合的残差也较大. GPS 和Galileo的轨道一致性显著优于GLONASS，90%的GPS卫星和67%的Galileo卫星横向差异小于20 mm，31天内平均轨道差异分别为19 mm和21 mm，约为GLONASS平均轨道差异的一半. 因此如果想要提高GLONASS钟差一致性必须提高轨道精度或者考虑横向轨道差异改正.

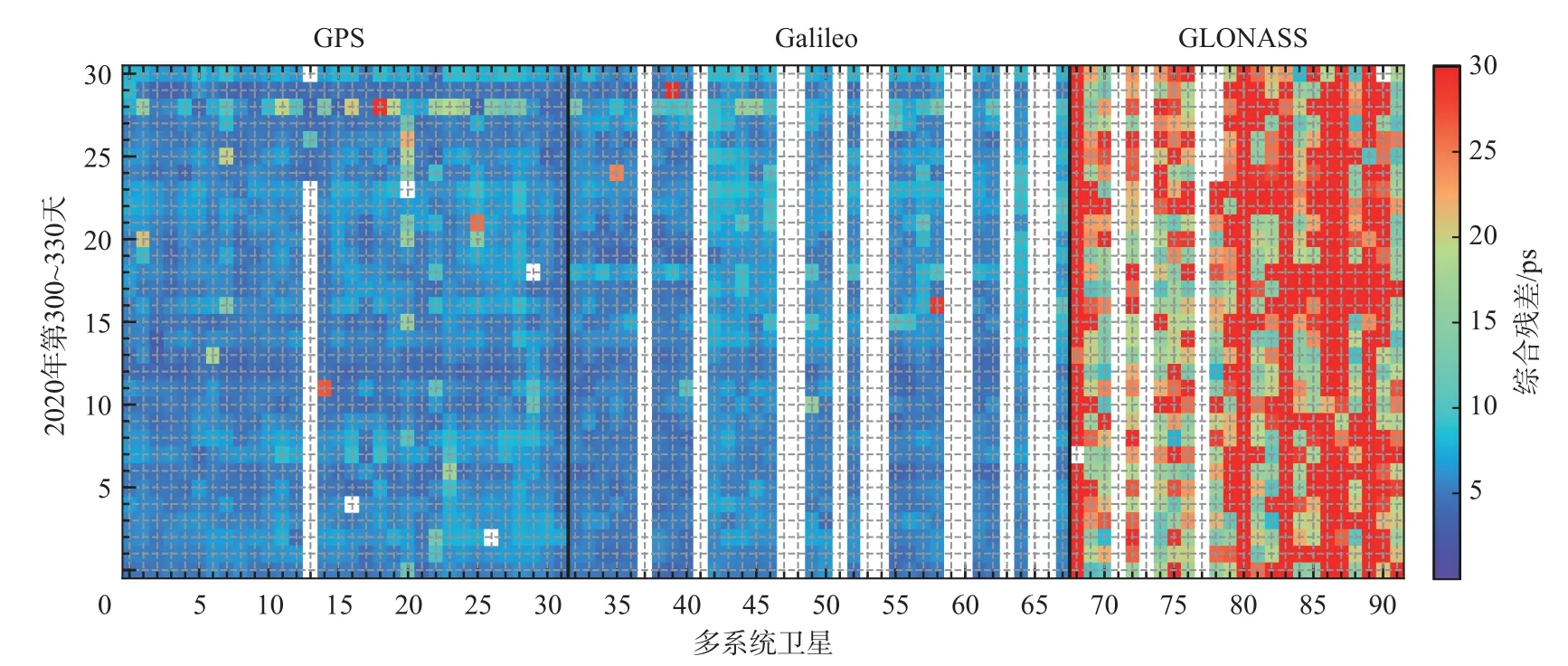
图2 GPS/Galileo/GLONASS卫星钟差综合残差

表2 GPS/Galileo/GLONASS 钟差一致性 ps

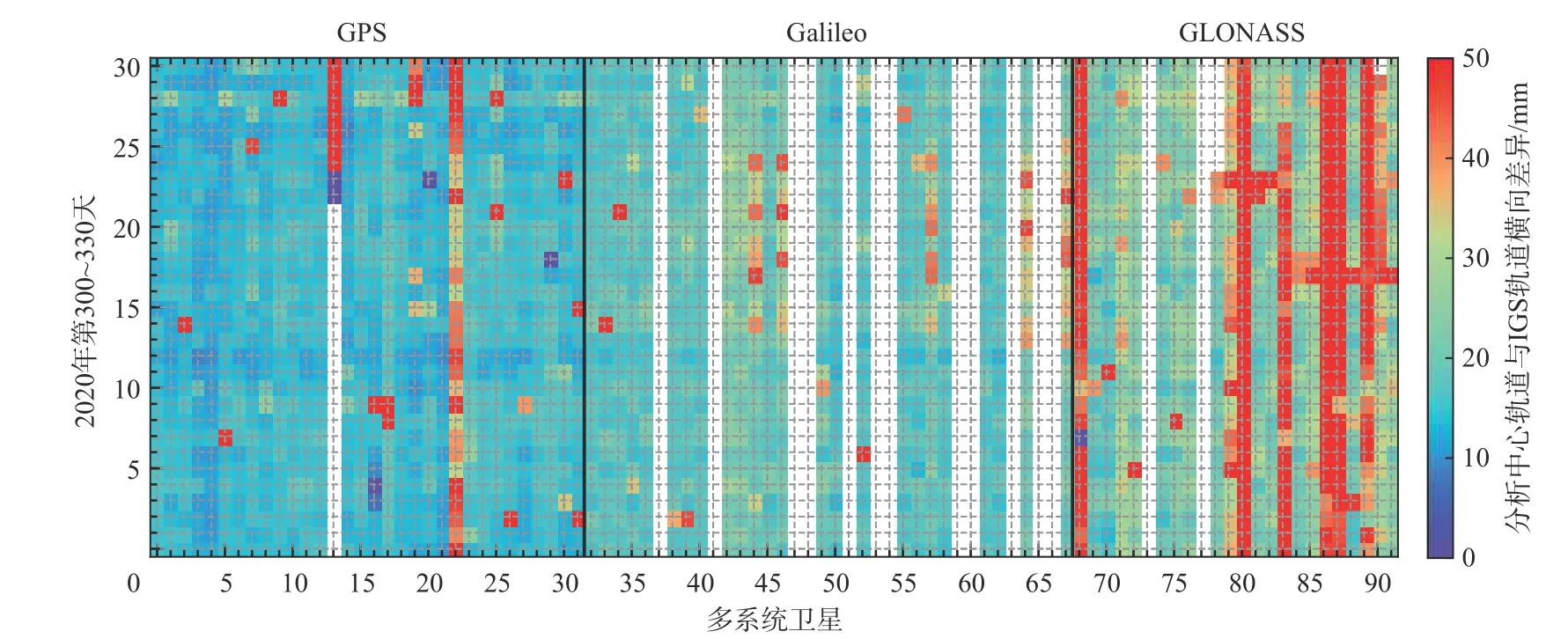
图3 GPS/Galileo/GLONASS 卫星切向和法向轨道差异

为了验证姿态改正对钟差综合的作用，对比了改正姿态前后的综合残差. 图4展示了姿态改正前后综合残差变化相对原始残差的百分比. 百分比为正说明改正姿态能减小综合残差. 由图4可知，GPS综合残差中姿态改正效果最明显的是两颗Block IIF卫星G24和G30，改正姿态后，综合残差的RMS分别从87.0 ps和62.0 ps减小为17.5 ps和10.0 ps. 姿态改正前后，Galileo和GLONASS钟差综合残差变化不明显. 进一步研究发现，2020年第300～330天期间各分析中心Galileo姿态差异较小，个别卫星地影期时姿态差异变大，但持续时间较短，图5分别展示了各分析中心GPS、Galileo和GLONASS卫星姿态差异较大的情况. 可以发现，对于GPS卫星G24和G30，各分析中心之间姿态差异可达到360°，并且持续时间长达12 h；而对于Galileo卫星E33和GLONASS卫星R11，各分析中心之间姿态差异最大分别为127°和185°，但持续时间小于1 h，因此姿态改正的影响并不明显.

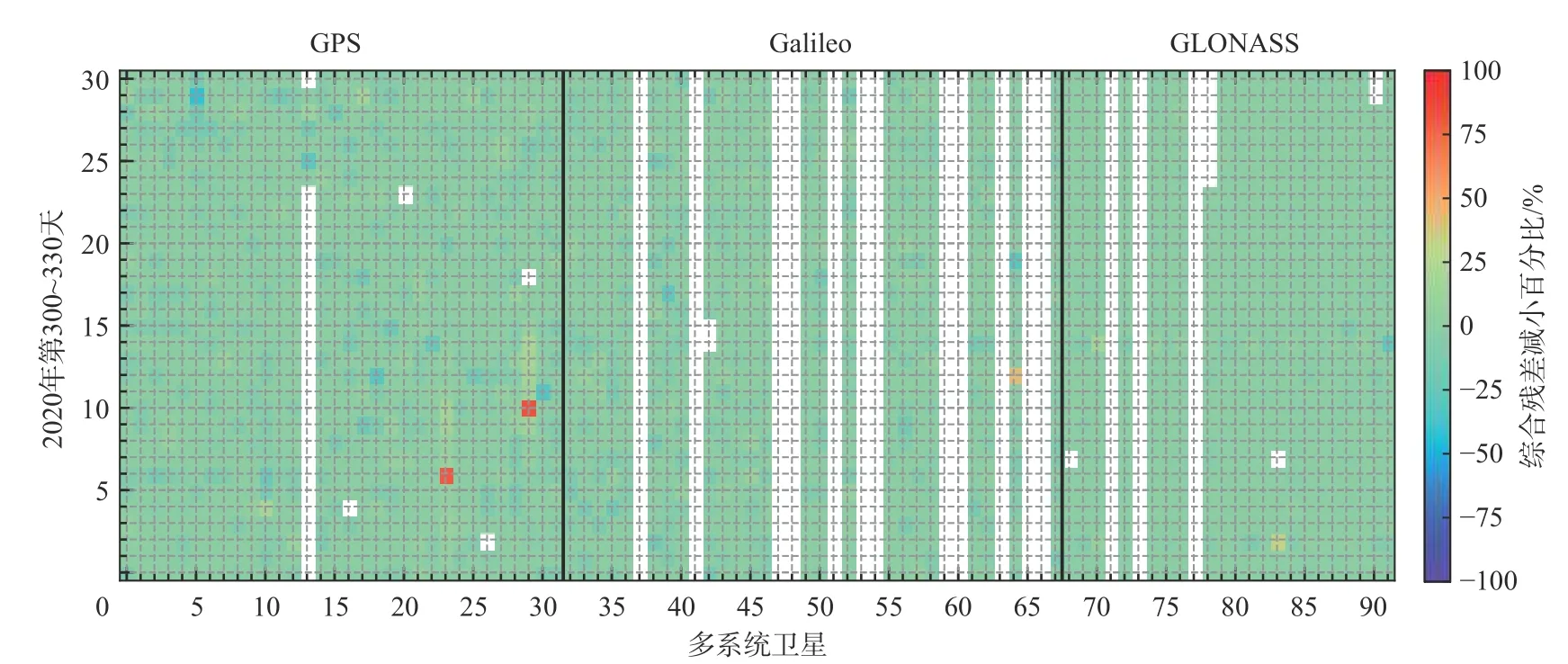
图4 顾及姿态改正后钟差综合残差减小的百分比

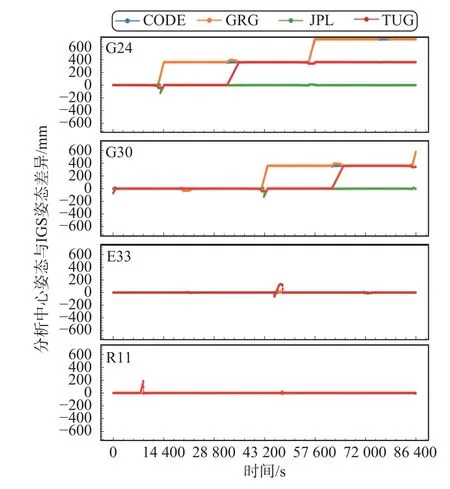
图5 不同卫星的分析中心间姿态差异

2.3 静态和动态定位实验

为了进一步测试综合产品的定位性能，使用综合产品及各分析中心产品对142个IGS测站进行PPP静态定位和动态定位测试. 图6展示了2020年第300～330天综合产品和各分析中心产品的多系统GNSS (GPS/Galileo/GLONASS) 动态定位精度. 其中，CMN和CMB均为综合产品，CMN表示钟差综合和定位时均未使用姿态文件进行改正，CMB表示使用IGS姿态文件作为参考姿态进行改正，且定位时使用IGS姿态产品. 总体而言，各分析中心产品的动态精度与综合产品精度相当，但综合产品的定位精度最稳定，31天内没有出现大幅的波动. 而各分析中心产品的定位精度常出现较大的波动，例如GRG在302和307等天动态定位RMS异常，东(E)方向RMS最大可达4 cm，约为其他分析中心的两倍. 进一步研究发现，在这些异常天，GRG产品中个别卫星钟差与别的分析中心产品间存在显著的非线性差异.钟差综合过程中可将这些钟差识别为粗差并且剔除，因此综合的产品不会受到影响. 这也验证了钟差综合产品能在保证产品高精度的前提下较单个分析中心的产品具有更稳定的性能. 相对于单个分析中心的产品，综合产品在E、北(N)、天顶(U)方向的动态定位精度最大可提升22.7%、16.7%和18.3%；31天静态坐标重复精度最大可提升38.2%、32.0%和14.0%.图6中CMB和CMN产品的定位精度在第315～330天基本重合，但在第300～314天，改正姿态的综合产品的定位精度显著优于未使用姿态的综合产品.31天内E、N、U方向平均动态精度提升分别为8.5%、10.3%和10.6%. 单个测站E、N、U三个方向平均动态精度提升最大可达65.3%，约为1 cm.图7为31天内静态和动态定位的统计精度. 可以发现，随着卫星系统的增多，定位精度不断提高. 虽然GLONASS目前各分析中心产品的一致性较差，但GPS/Galileo/GLONASS三系统综合产品定位精度仍然优于GPS单系统和GPS/Galileo双系统综合产品. 相对于单GPS综合产品，GPS、Galileo和GLONASS三系统综合产品在E、N、U三个方向的动态定位精度可分别提升28.5%、23.0%和26.4%；31天静态坐标重复精度可提升19.2%、5.6%和7.5%.

图6 2020年第300～330天多系统GNSS(GPS/Galileo/GLONASS) PPP动态定位精度

图7 PPP静态和动态定位统计精度

3 结束语

针对目前多系统GNSS的发展趋势，本文研究了一种顾及姿态改正的多系统GNSS钟差综合策略. 该方法顾及了各分析中心GNSS精密钟差估计过程中的多种差异，包括轨道差异、基准差异、初始钟偏差差异等. 相对于传统的GPS精密钟差综合，进一步考虑了卫星姿态和GNSS系统间偏差的影响. 卫星姿态产品的引入使得各分析中心卫星钟差产品在地影期的一致性更好. 本文使用2020年第300～330天的IGS第三次重处理产品进行综合测试. 改正姿态后，GPS钟差综合残差的RMS最大可减小80%，并利用综合产品进行PPP静态和动态定位实验. GPS/Galileo/GLONASS三系统综合产品的定位精度显著优于GPS单系统和GPS/Galileo双系统综合产品. 相对于单GPS综合产品，GPS、Galileo和GLONASS三系统综合产品在E、N、U三个方向的动态定位精度可分别提升28.5%、23.0%和26.4%；31天静态坐标重复精度可提升19.2%、5.6%和7.5%. 并且，综合产品能在保证产品高精度的前提下较单个分析中心的产品具有更稳定的性能. 相对于单个分析中心的产品，综合产品在E、N、U方向的动态定位精度最大可提升22.7%、16.7%和18.3%. 与此同时，相对于未顾及姿态改正的综合产品，单个测站使用顾及姿态改正的综合产品时动态定位精度最大可提升65.3%，约为1 cm. 总体而言，本文实现的多系统GNSS钟差综合策略可为分析中心多系统GNSS产品综合提供参考.