基于改进CRITIC-VIKOR法的装配式构配件供应商选择分析

刘祖威，王首绪

（长沙理工大学 交通运输工程学院，湖南 长沙 410114，E-mail：99088472@qq.com）

装配式建筑具有高质量、工厂化程度高、低能耗、工期可控性强的显著优势，是建筑行业向工业化转型发展的重要方向。设计、生产及安装施工作为装配式建筑的三大管控要点，对装配式建筑的开发建设起到了决定性的作用。其中生产环节的关键在于供应链管理，供应链管理的核心又是供应商管理[1]。供应商作为装配式构配件供应链的源头，直接决定了构配件的质量、成本等关键内容。与互惠的供应商建立长期有效的合作能够降低企业的成本、减少采购风险、增强管理弹性[2]。因此，能否客观科学地对装配式构配件供应商进行评价和选择，将会对装配式建筑的顺利建设产生直接影响。

传统的装配式构配件供应商决策分析的方法有德尔菲法和招标法。德尔菲法[3]是通过咨询大量专家对备选供应商的意见，得出结论的过程，德尔菲法具有操作简单、分析速度快的优势，但完全依靠专家人员的主观经验，缺少客观的研究与论证。招标法是在工程实践中最常用的供应商评价方法，是基于竞争思维和底线思维来选择供应商，应用广泛，可靠性强，但将价格摆在了十分重要的位置，且该方法耗时长、操作复杂，不能适用时间紧张的供应商选择分析。随着装配式建筑的发展和供应商管理复杂程度的提升，单一的传统的供应商选择方法难以科学地做出决策分析，因此需要引入更加先进的理论来指导供应商的决策分析。王春红等[4]构建了大数据平台，利用BP神经网络算法优选供应商，不断扩充数据平台并接续优选供应商。杨斯玲等[5]开发了基于灰色系统的集对分析法，通过显示出供应商各项能力的差异性来评价选择绿色建筑供应商。郭彬等[6]构建了基于ANP赋权的理想解法（TOPSIS），通过计算正负理想解的相对贴进度来选择供应商。Majid Azadi等[7]在模糊条件下整合了数据包络分析（Data Envelopment Analysis）和拉塞尔测度模型（Russell Measure Model）来选择最优的供应商。姚强[8]采用G1法和变异系数法组合赋权，并提出了马氏距离改进TOPSIS的方法计算供应商的排序。卢虹林等[9]改进了最优最劣法并与云物元理论相结合，获得了供应商的排序和评价等级。

综上，目前供应商的选择分析主要存在如下问题：一是权重计算过度依赖有关专家的专业知识和经验，主观性过强；二是大多忽略了评价指标间存在的关联性的问题，只考虑了指标的数值，没有考虑指标的深度信息；三是决策方法的精度和灵活性不足。鉴于此，本文建立了装配式构配件供应商评价指标体系，并构建基于改进CRITIC赋权、灰色关联系数为决策矩阵的VIKOR装配式构配件供应商决策分析模型。从而实现装配式构配件供应商的评价和决策分析，为装配式构配件供应商的选择提供了一种决策参考。

1 装配式构配件供应商管理分析

1.1 装配式构配件供应商管理特点

装配式建造为建筑行业高效节能、工业化、可持续的发展提供新的思路[10]。装配式建筑与传统建筑在管理思想上有着很大的不同，其中最为宏观的不同之处在于传统模式是设计、施工、采购分离的阶段性管理；装配式建筑受模块化、工厂化建造方式的影响，需采用整体集中的管理模式。如图1所示，装配式建筑的利益相关方、建设流程、管理阶段等相互交错，使管理更具复杂性，因此装配式项目大多采用EPC总承包的组织管理模式。此外，在采购对象方面，传统建筑购买的是水泥、钢筋、沙石等原材料；而装配式建筑购买的是预制墙板、楼梯等构配件。装配式预制构配件的原材料采购、深化设计、生产养护、出厂运输都由供应商承担，因此除了传统的管理内容外还必须对装配式构配件供应商进行有针对性的组织管理。

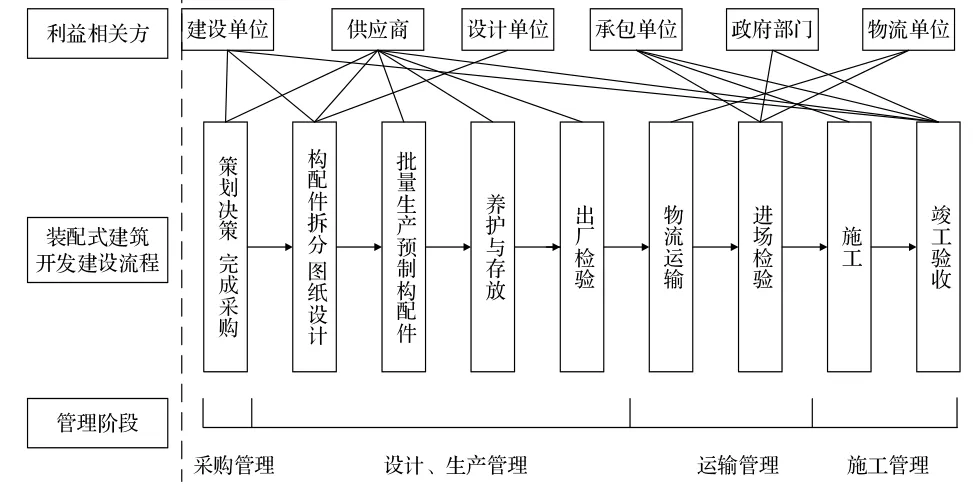
图1 装配式建筑管理框架

TQC三大目标（工期、质量和成本）也是装配式构配件供应商管理的重点。对于工期控制，预制、高效是装配式建造的特有优势，但供应商也必须按照约定的时间分批次提交预制构配件，以保证工程建设按期完工。对于质量控制，装配式构配件的性能、精度、与工地现场的适配程度等对整个装配式建筑有着巨大的影响，必须对供应商的产品品质进行严格把关。对于成本控制，成本问题是制约装配式建筑发展的关键，选择成熟负责的供应商，与之建立协调管理机制，能够有效地节约成本、实现双赢[11]。对于总承包方而言，供应商管理不仅仅需要把关供应商产品事宜，也需要保证装配式构配件供应链的稳定运行。因此还要考虑供应商的物流运输、科研、企业发展等多方面的能力。所以，如何选择和分析装配式构配件供应商变得至关重要。

1.2 建立装配式构配件供应商评价指标体系

科学地进行供应商选择分析的关键，在于合理地构建装配式构配件供应商评价指标体系。本文遵循系统性、简洁性、客观性、可操作性、定性定量相结合等基本原则，根据供应商管理的重点内容倒推，结合装配式建筑相关政策文件和工程案例，以工期、质量及成本三大目标为基础；考虑预制构配件的物流运输及供应商的专业能力；另外也兼顾了供应商企业共有的综合能力，初步建立了评价指标体系；进一步通过参考已有文献、资料分析、征询与访谈等过程进行指标的剔除、筛选和提炼，最终得到产品品质、经济与成本、物流运输、供应商专业能力、供应商综合能力5项一级指标，以及细化的17项二级指标，相关信息如表1所示。

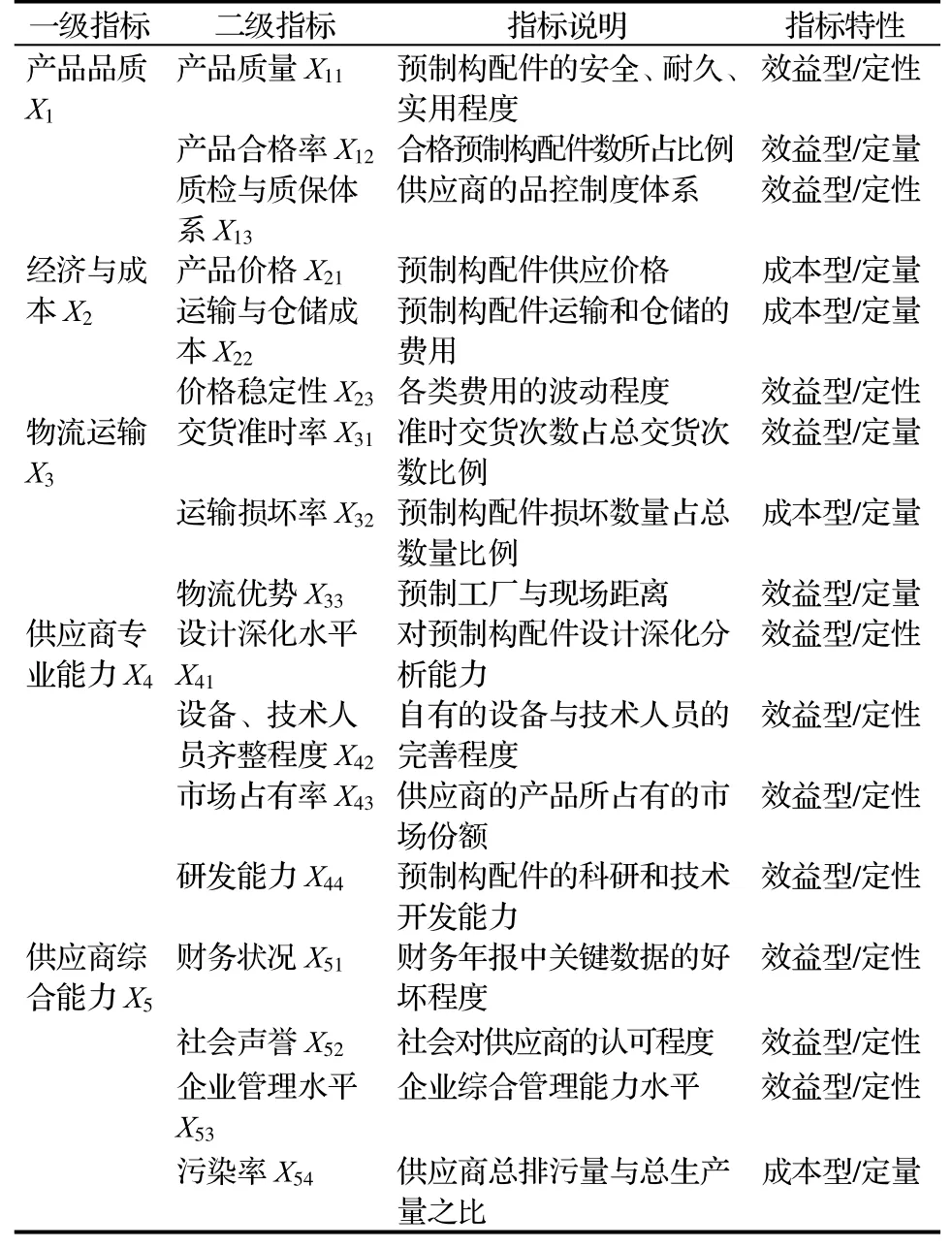
表1 装配式构配件指标体系及其说明

2 装配式构配件供应商评价模型

2.1 改进CRITIC模型

Diakoulakai.D[12]在1995年提出了CRITIC模型，是计算指标间的相关性和冲突性确定权重的理论方法。利用Pearson相关系数表征相关性，其值越大，表示相关程度越高；利用标准差表征冲突性，其值越大，表示指标越离散，信息量越大。但是传统CRITIC模型中采用的相关系数可能出现负数的情况，会导致得到错误的结果；标准差衡量指标冲突性，精确度太低、不能表示出指标分布的均衡程度、当数据的量纲和量级不同时，会出现衡量失真的情况。因此，本文在计算中将相关系数取绝对值；引入基尼系数取代标准差来衡量指标间的冲突性[13]。得到改进CRITIC模型，其步骤如下：

（1）假设有m个方案，n个指标，建立矩阵A=[aij]m×n，aij，表示第i个方案第j个指标的数值。

（2）数据处理。为了消除不同指标之间的差异，效益型指标进行正向化处理；成本型指标进行逆向化处理。计算得到标准化矩阵B=[bij]m×n。

（3）计算得到相关系数矩阵R=[rij]m×n，rij是第i个指标与第j个指标间的Pearson相关系数，其计算公式为：

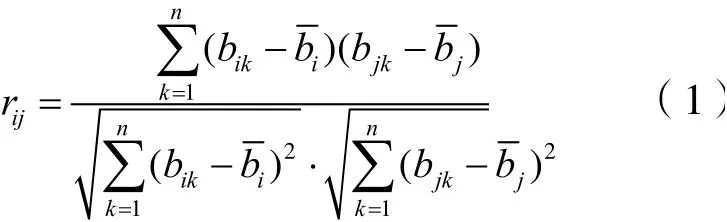
（4）计算基尼系数γj。

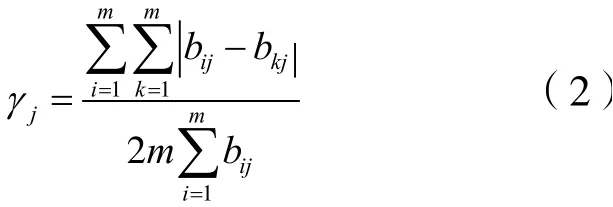
其中，γj∈[0，1]。γj越接近1，表示j指标的信息分布越不均衡，信息量也就越大；γj越接近0，表示j指标的信息分布越均衡，信息量也就越小。

92例宫颈鳞癌组织和30例正常宫颈组织蜡块标本均来源于2008年1月—2012年4月在哈尔滨医科大学附属肿瘤医院妇科住院手术患者，均签署患者知情同意书，临床资料完整。30例正常宫颈组织来源于同期住院因子宫肌瘤手术患者，年龄为38～55岁，中位年龄为47.6岁。宫颈癌患者年龄29～62岁，中位年龄为45岁。宫颈癌参照FIGO(2009)分期，Ⅰ期62例，Ⅱa期30例。由两位病理科医生对全部标本进行复核确定细胞分化程度及肿瘤类型。

（5）计算信息系数gj。因为指标间会存在正相关和负相关的情况，为了保证最终结果的正确，取Pearson相关系数的绝对值进行信息系数的计算。计算公式如下：

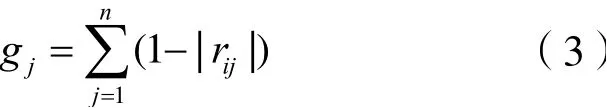
（6）计算指标综合信息量Gi并确定权重ωj。Gi越大，表示i指标的信息量也就越大，则相对应的权重也会越大。计算公式如下：

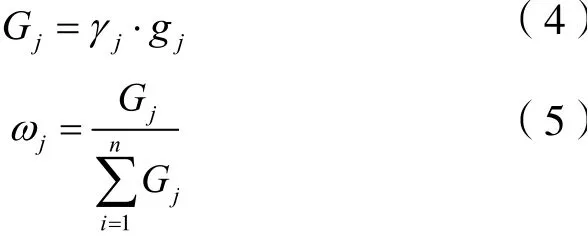
2.2 灰色关联矩阵的VIKOR法

灰色关联分析法是一种依据样本数据建模、生成序列并挖掘系统本身关联规律的方法[14]。因此，使用灰色关联系数矩阵作为VIKOR法的决策矩阵，能充分挖掘数据信息、考虑指标间的关联性并且能有效提高精度。VIKOR法是Opricovic[15]提出的一种基于理想解的妥协解排序的多属性决策方法。该方法相比理想解法（TOPSIS）更加稳定可靠；相比于其他多属性决策方法具有充分利用原始数据、能对计算结果进行验证并修正的优点。其步骤如下：

（1）计算理想序列b0j。在B=[bij]m×n取每个指标的最大值得到理想序列，计算公式如下：

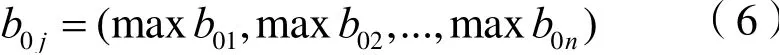
（2）计算关联系数矩阵C=[cij]m×n。

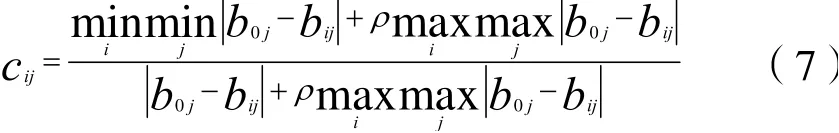
式中，cij为关联系数；ρ为分辨系数，取0.5。

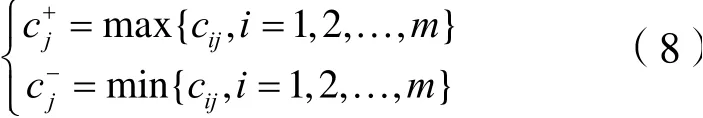
（4）计算最大群体效益值Si、最小个体遗憾值Ri和利益比率值Qi。计算公式如下：

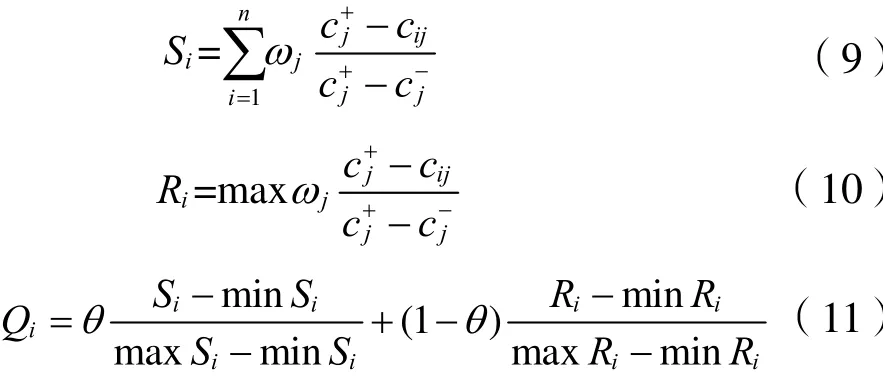
式中，ωj是用改进CRITIC求得的指标客观权重；θ为决策系数，θ∈[0，1]。

（5）对各个装配式构配件供应商的Si、Ri和Qi的数值从小到大排序，并进行验证和修正。记按照Qi排序的最优和次优供应商分别为T1和T2。只有最优供应商T1满足以下两个条件才是最优方案。

条件一：Qi(T2)-Qi(T1)≥1/(m-1)。

条件二：最优供应商T1的Si、Ri的排序至少有一个仍是第一位排序。

若条件一、条件二都同时成立，T1为最优供应商；若只有条件一成立，T1与T2均为最优供应商；若只有条件二成立，则不满足条件一的所有供应商都为最优供应商。

3 案例应用

长沙市某工程项目采用EPC总承包模式开发建设装配式建筑，需采购大批量的装配式预制构配件，经过资质审查和初步筛选，确定了5个装配式构配件供应商（分别记为P1，P2，P3，P4，P5）。通过对这5家备选供应商的实地调查、资料分析，得到相关的基本定量数据；对于定性指标采用专家打分法获得原始数据，打分专家共计10名，分别来自行业内的研发设计、生产、施工、运营、财务、管理等岗位及相关领域的高校学者。

3.1 应用步骤

（1）将获取到的原始数据中的效益型指标进行正向化处理；成本型指标进行逆向化处理得到标准化矩阵。根据式（1）计算Pearson相关系数，如r11=1，r11=0.807，同理计算得到全部相关系数rij；根据式（2）~式（5）分别计算得到基尼系数γj、信息系数gj、综合信息量Gi和改进CRITIC客观权重ωj。

（2）根据式（6）计算得到一个元素全为1的灰色关联理想序列；进一步根据式（7）~式（8）得到关联系数矩阵，并以关联系数矩阵作为VIKOR法决策矩阵计算正负理想解，如表2所示。

（3）结合表2中已经求得权重ωj=（0.043，0.042，0.048，0.054，0.058，0.055，0.047，0.071，0.070，0.061，0.081，0.064，0.051，0.082，0.063，0.051，0.060）并根据式（9）~式（11），计算θ=0.5时，Si、Ri和Qi的值并对其从小到大进行排序，其结果如表3所示。从表3可知，Qi(T2)-Qi(T1)=0.6489-0.0000=0.6489>1/(m-1)=1/(5-1)=0.25，条件一成立；P3供应商的Si排序和Ri排序都排在第一位，条件二成立；检验表明P3为妥协折衷（θ=0.5）条件下的最优的装配式构配件供应商。

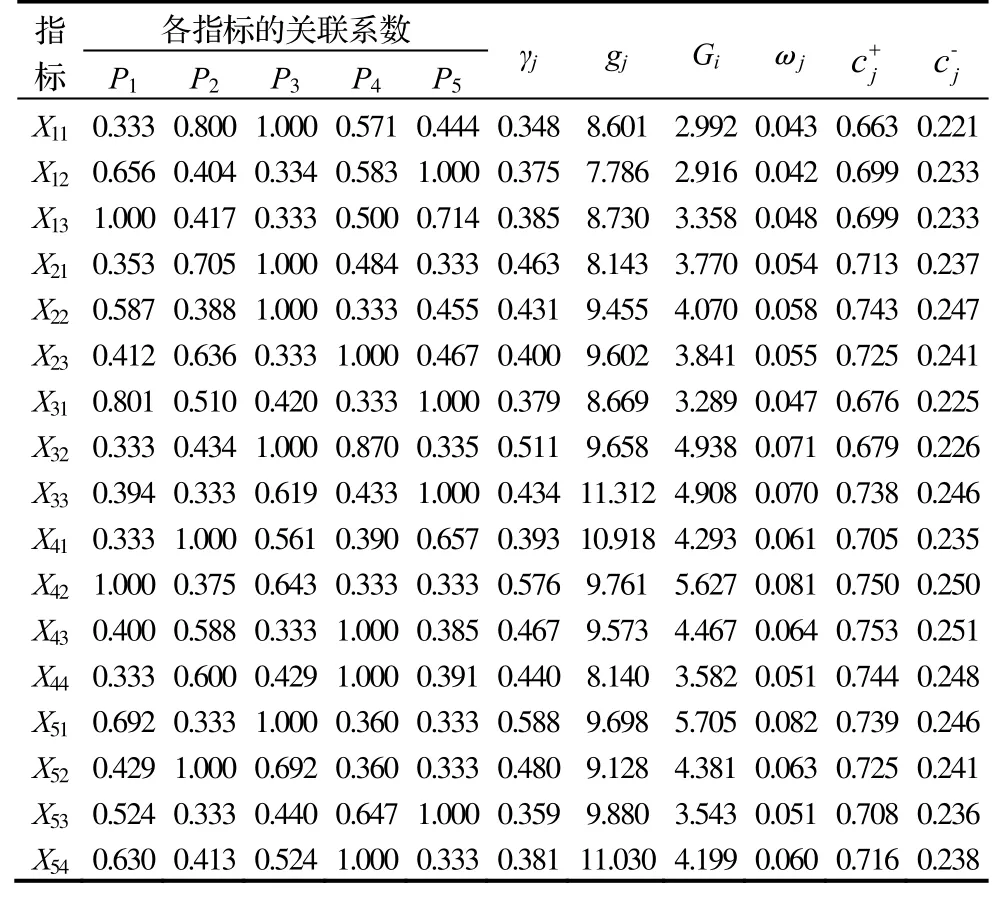
表2 指标关联系数、改进CRITIC权重以及相关过程数据

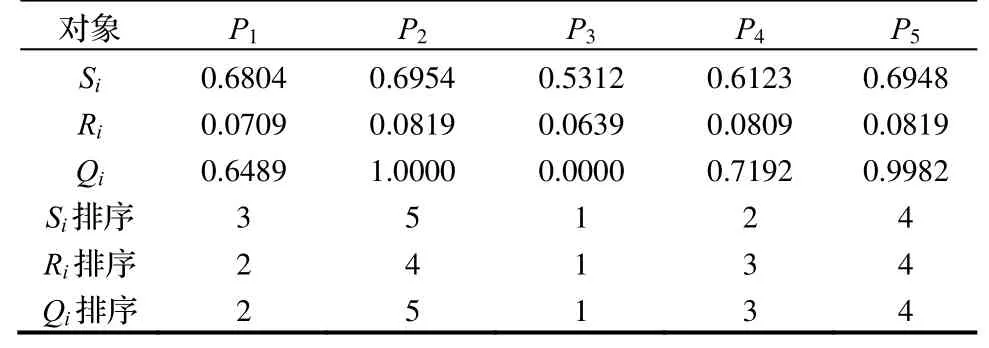
表3 装配式构配件供应商Si、Ri和Qi值及排序（θ=0.5）

3.2 对比分析

（1）不同决策系数的影响。VIKOR法中的决策系数θ不同的取值代表了不同的实际意义且会影响最终的决策结果。若θ<0.5，表示决策时倾向于最小化个体遗憾解；若θ>0.5，表示决策时倾向于最大群体效益解；若θ=0.5，表示决策时倾向妥协折衷解。不同的θ条件下VIKOR法有不同意义的最优解，本文在[0，1]之间共取5个不同的θ值进行敏感性分析。不同决策系数θ条件下的Qi值及供应商排序结果如表4所示，且各θ条件下的排序均通过验证。由表4可知，供应商P3的5次Qi值均为最小；供应商P5的5次Qi值均为第二大；供应商P2的5次Qi值均为最大；供应商P1，P4受θ影响排序略有变动。由上可知，本案例条件下，供应商的选择排序对决策系数θ不敏感，具有稳定性。

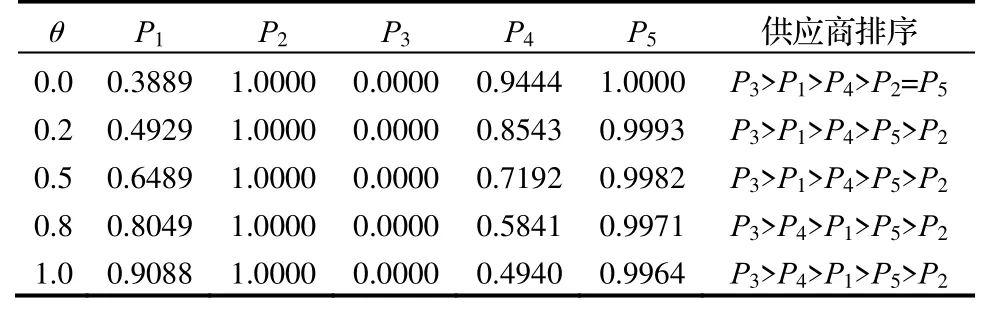
表4 不同决策系数θ条件下的Qi值及供应商排序结果

（2）不同决策矩阵的影响。为了挖掘评价指标间的信息、消除指标间关联性的问题，引入了灰色关联分析法获得关联系数矩阵，来替代原始的决策矩阵。鉴于此，本文采用原始数据作为决策矩阵（其他条件一致）进行VIKOR供应商选择分析，并进行对比研究决策矩阵对供应商选择决策的影响，结果如表5所示。由表5可知，不同决策矩阵得到的最优供应商都是P3，但与关联系数矩阵条件下的排序差异较大。这是因为原始数据矩阵VIKOR法下的排序，没能考虑到指标间的关联性，导致分析失真，缺少一定的准确性。

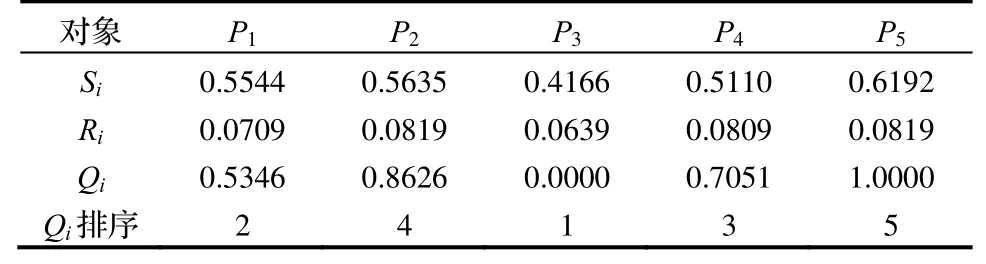
表5 原始数据决策矩阵Si、Ri和Qi值及排序（θ=0.5）

4 结语

本文针对装配式构配件供应商决策分析过程中指标赋权主观性大、指标间存在关联性、未能充分挖掘数据信息、决策方法精度和灵活性不足，导致供应商的选择分析出现偏差的问题，提出了基于改进CRITIC赋权，关联系数作为决策矩阵的VIKOR供应商选择分析模型。以装配式构配件供应商管理中的工期、质量、成本3项基本内容为依托，考虑预制构配件的物流运输及供应商的专业能力，兼顾了供应商企业共有的综合能力，有针对性地建立了产品品质、经济与成本、物流运输、供应商专业能力、供应商综合能力5项一级指标，以及17项二级指标的装配式构配件供应商评价指标体系。在计算信息系数gj时将相关系数取绝对值及引入基尼系数改进CRITIC模型。调整计算手法以保证CRITIC客观赋权的准确；基尼系数表征指标冲突性充分提高了精度。关联系数作为决策矩阵能有效避免指标相互关联和计算重合的问题；使用VIKOR法充分利用指标的数据信息。通过案例应用并从决策系数和决策矩阵两个角度进行对比研究，验证了该方法的灵活性和可行性。