基于修正SHAPLEY值的全过程工程咨询利益分配研究
2022-05-18孙琳琳刘丽佳
孙琳琳,赵 允,刘丽佳
(1. 山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590;2. 山东科技大学 土木工程与建筑学院,山东 青岛 266590,E-mail:1551678145@qq.com)
自2017年2月国务院办公厅发布的《关于促 进建筑业持续健康发展的意见》[1]中提出培育全过程工程咨询,首次明确了全过程工程咨询的理念,并鼓励企业间采取联合经营、并购重组等方式发展,到2019年3月国家发改委、住建部发布《关于推进全过程工程咨询服务发展的指导意见》,各省市相继发布有关全过程工程咨询方面的政策文件,彰显了我国从上级机关到下级政府十分重视推行全过程工程咨询,也表明了全过程工程咨询将成为或已成为建筑行业的热点领域[2,3]。目前,由于我国现有的法规体系一定范围内约束了全过程工程咨询行业的发展,再加上全过程工程咨询本身涉及的业务流程多,国内工程咨询行业的企业资质和人才等方面良莠不齐[4],因此在我国能够独立提供全过程工程咨询服务的企业凤毛麟角,大多以联合体形式开展,相较于传统“碎片式”的咨询服务,以联合体形式开展的全过程工程咨询服务拥有显著优势,能够最大程度上节约资源[5,6]。
然而,我国在大力推行全过程工程咨询的同时,不得不面临一个难题:即全过程工程咨询中联合体成员的利益如何分配。利益分配是全过程工程咨询项目能否成功的关键,而由于该服务在我国刚刚兴起,其组织结构、取费标准及利益分配等问题都没有规范性文件,缺少理论层面和实践层面的研究[7]。因此,本文采用Shapley值法对全过程工程咨询项目联合体成员间利益分配进行分析,在综合考虑各个影响因素的前提下,对传统Shapley值模型进行修正,建立更为准确的利益分配模型[8],使各利益主体的分配更加公平、公正、合理。
1 基于Shapley值的利益分配模型
Shapley值法是由Shapley L. S.提出的用于解决多人合作对策问题的方法,常用于解决合作联盟利益分配问题,能够最大程度上保障利益分配的准确性[9,10]。
当N个参与方进行某项经济活动时,参与方之间的多种组合方式都能产生相应的收益。如果各参与方之间的经济活动是非对抗性的,参与方数量的增加不会造成收益降低,那产生最大收益的方式就为N个参与方合作,Shapley值法就是分配项目最大利益的一种方法[8]。因此,假设全过程工程咨询联合体中有n个项目成员,它们构成的集合为N,Y∈N是N中的一个联盟,由若干个项目成员组成。Φi是n个项目成员共同参与下i方得到的利益分配值,被称为Shapley值。
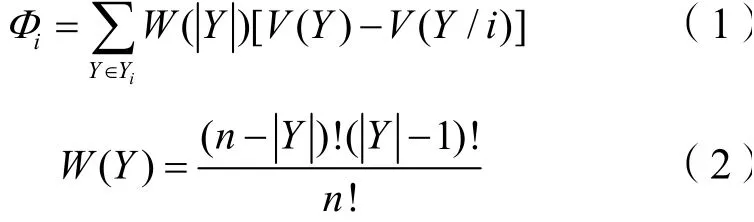
式中,W(|Y|)为加权因子,即Shapley值系数;V(Y)为联盟Y的收益;V(Y/i)为联盟中除掉参与方i后获得的收益;Y为联盟中参与方的个数;n为成员的数量,i=(1,2,…,n)。
2 修正Shapley值的利益分配模型
Shapley值法是根据联合体成员对全过程工程咨询项目的边际贡献进行利益分配,但是该模型认为其他因素对利益分配的影响程度均为1/n,忽略成员之间的相互作用。而在全过程工程咨询项目中,成员的风险分担、投入比重、项目贡献度、合同履约度、新技术运用、行业领导力等因素对联合体成员的利益分配有着重要影响[9]。因此,引入相关因素对Shapley值模型进行修正,使全过程工程咨询项目中的联合体成员利益分配趋于公平、公正、合理。
2.1 影响全过程工程咨询项目利益分配的因素
在全过程工程咨询项目中,综合考虑利益分配原则后(合作共赢原则、投入风险与利益相称原则、公平兼顾效率原则、结构利益最优原则等[11]),对影响全过程工程咨询项目利益分配的因素进行分析及专家咨询,将影响全过程工程咨询项目利益分配的因素分为确定性因素和不确定因素[12],如图1所示。
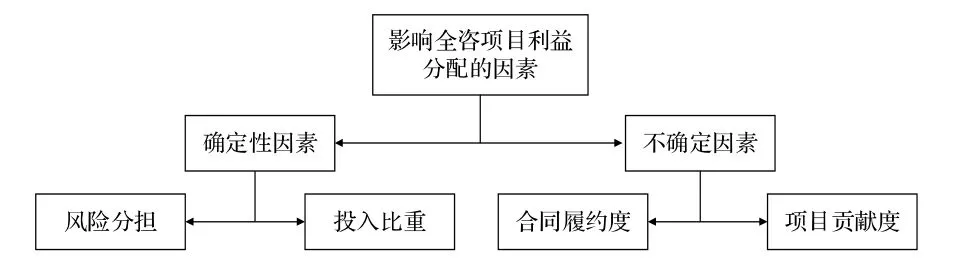
图1 影响全过程工程咨询项目利益分配的因素
(1)风险分担。通常,风险与收益呈正相关,风险越高意味着收益越多。以联合体形式的全过程工程咨询项目,涉及主体多,时间跨度大,直接导致项目风险大。但通过联合体成员间合理分配风险,可以降低其风险水平,增加项目收益,因而风险分担是影响全过程工程咨询项目利益分配的关键因素。具体包括投资风险、合同风险、管理风险和运营风险4个风险因子。
(2)投入比重。全过程工程咨询的时间跨度是从前期投资、决策到项目实施、运营阶段,项目周期长、规模大,项目实施过程中要引入大量资源,其中涉及资金、设备和人力等。一般而言,企业对项目进行投资,目的是获得利益,投入越多期待回报越多,因而投入比重在全过程工程咨询项目利益分配中起到重要作用。
(3)合同履约度。目前,全过程工程咨询项目大多以联合体形式开展,在全过程工程咨询项目开展期间,若项目中某个成员为了自身利益,贸然违反合同条件,将导致整个全过程工程咨询项目的利益受到损害。合同履约度是项目参与方对合同内容履行程度或使项目取得最大收益的努力程度[13,14],因而,把合同履约度纳入全过程工程咨询项目利益分配的考虑因素,一定程度上可以提高联合体成员的积极性,规范成员行为,严格遵循合同约定,使全过程工程咨询项目利益最大化。
(4)项目贡献度。本文研究的项目贡献度与Shapley值的边际贡献率不同,指的是全过程工程咨询项目在遇到突发状况或紧急情况对项目的质量、工期及利益等方面造成威胁时,项目成员进行挽救而做出的额外贡献或牺牲[13]。目前,全过程工程咨询服务在我国仍处于探索期,相关的政策法规还不完善,项目成员在处理突发状况时必须做出贡献或牺牲,所以综合考虑后将项目贡献度纳入全过程工程咨询项目利益分配的考虑因素之一,可以激发项目成员牺牲或贡献精神的积极性。
2.2 基于修正Shapley值的利益分配模型的建立
2.2.1 利益分配模型
根据对影响全过程工程咨询利益分配因素分析,构建修正因素集合J={j},(j=1,2,3,4),分别表示影响全过程工程咨询利益分配的4个因素,从而形成影响全过程工程咨询利益分配因素的修正测度值[14],如表1所示。

表1 影响全过程工程咨询利益分配因素的修正测度值
根据表1构建修正矩阵G,对构建的修正矩阵G进行归一化处理。通过强制打分法,确定影响因素对全过程工程咨询项目利益分配的程度:P=[P1,P2,P3,P4]T;并且确定修正系数:得到修正后全过程工程咨询项目联合体成员的利益分配值:
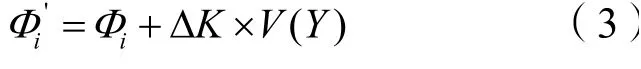
其中,Ki为修正后4个影响因素对全过程工程咨询项目参与方利益分配的综合影响程度。
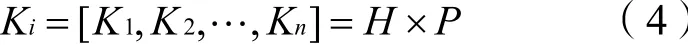
2.2.2 影响因素参数的确定
(1)风险分担是全过程工程咨询项目利益分配的重中之重,结合上文选取了4个风险因子:投资风险、合同风险、管理风险、运营风险,确定其权重,由此确定项目各成员的风险分担比例,其中由于全过程工程咨询项目风险涉及的二级指标较多,故而采用模糊综合评价法确定全过程工程咨询项目利益分配的风险分担比例g11、g21、…、gn1[15]。
(2)在投入比重方面,全过程工程咨询项目联合体成员的投入涉及资金、设备及人力等,且各成员投入比例均不同,因而在确定联合体成员投入权重时应该将不同的资源量化,得到全过程工程咨询项目联合体成员的投入比重g12、g22、…、gn2。
(3)合同履约度是利益主体对合同约定内容的履行情况,要对各成员的履行情况进行定量分析,确定全过程工程咨询项目联合体成员的合同履约度g13、g23、…、gn3。
(4)项目贡献度是联合体成员在面对突发状况时做出的贡献或牺牲,其确定方法同上,得到联合体成员的项目贡献度g14、g24、…、gn4。
2.2.3 修正Shapley值利益分配模型的方法
考虑Shapley值模型认为各因素对全过程工程咨询项目利益分配的影响程度均为1/n,忽略各成员之间的作用,进而对其进行系数修正。在修正Shapley值模型部分,确定风险分担比例时采用模糊综合评价方法,其中借助层次分析法确定投资风险、合同风险、管理风险、运营风险4个风险因子权重。利益分配修正模型的重点在于确定修正矩阵G,修正矩阵G中关键是用模糊综合评价法进行风险评价确定成员的风险分担比例,最终得到修正系数ΔK。
由上述4个风险因子,确定风险评价的因素论域:ωi=[ω1,ω2,ω3,ω4];由此确定风险因子等级论域:V=(v1,v2,v3,v4);再由专家对全过程工程咨询项目参与方的风险分担进行打分评价,构建模糊综合评价关系矩阵D1、D2、...、Dn;最后,确定风险评价因素的权向量,计算全过程工程咨询项目联合体成员的风险分担系数:g11、g21、…、gn1。
3 具体案例分析
假设在M市和Y市间建设高速公路,项目拟采用全过程工程咨询模式,全长30km,公路为双向四车道。项目概算总投资为71600万元,工期12个月。通过招投标,确定由A公司牵头组建的联合体成功中标该项目,联合体其他成员为B和C公司,其中:A为设计公司,具有设计甲级资质,负责项目勘察和设计工作;B为咨询公司,负责造价咨询
和项目管理工作;C为监理公司,主要负责工程监理工作。经过估算,该高速公路项目采用全过程工程咨询模式联合体成员的利益为3000万元。若由联合体成员中的A设计公司单独完成,考虑其自身管理水平、项目风险大小等因素,估算A公司获得利益为800万。同理可得B、C公司获得利益分别为400万、600万。若由联合体中两家公司共同完成,相比于一家公司单独完成时考虑的诸多因素一定范围内可削弱其负面效果,则估算可知:A和B公司合作完成利益为1500万,A和C公司为1700万,B和C公司为1200万。根据上述背景,对高速公路全过程工程咨询项目联合体成员的利益分配进行分析。
3.1 传统Shapley值法计算项目参与方的利益分配
高速公路项目由A、B、C 3家公司共同完成,项目全部收益为3000万元,即V(A∪B∪C)=3000;3家独自完成利益为800万、400万、600万,V(A)=800万,V(B)=400,V(C)=600;AB合作完成利益为1500万,AC为1700万,BC为1200万,即V(A∪B)=1500,V(A∪C)=1700,V(B∪C)=1200。利用Shapley值计算项目各成员的利益分配值:
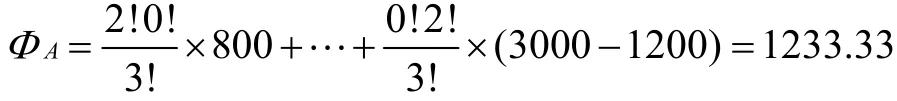
同理可得ΦB=783.33万元,ΦC=983.33万元。由此可知,相比A、B、C各公司单独完成时获得利益,项目成员之间共同合作完成的利益更大。
3.2 利用修正后Shapley值模型计算项目参与方的利益分配
3.2.1 确定参数,构建修正矩阵
根据模型修正步骤,首先确定修正矩阵G,方可进行模型计算部分,本部分针对风险分担、投入比重、合同履约度及项目贡献度4个因子,借助修正模型的方法确定各因素系数。
(1)风险分担。基于模糊综合评价法的风险评价。①对于全过程工程咨询项目的风险评价因素论域,采用层次分析法—通过指标间两两比较,构建风险分担矩阵,确定项目风险分担部分4个风险因子权重,得到风险评价的因素论域:ωi=(ω1,ω2,ω3,ω4)=[0.45,0.15,0.07,0.33];②确定风险等级论域:V=(v1,v2,v3,v4)=(0.1,0.3,0.5,0.7,0.9),代表风险等级:高、较高、一般、较低、低;③建立模糊综合评价关系矩阵D1,同理得D2、D3;④计算项目各参与方风险分担系数:g11=ωi×D1×VT=0.525,g21、g31分别为0.450、0.450。

(2)投入比重。根据合同约定,公司A、B、C的投入比重分别为0.5、0.3、0.2。针对投入比重部分存在不可量化指标,也可用模糊综合评价进行计算,但计算结果与合同约定的比重差别不大,故而采用合同约定部分得投入比重确定系数g12=0.5、g22=0.3、g32=0.2。
(3)合同履约度。假定全过程工程咨询项目有措施使参与方能够以最大的努力程度来实现项目的总体利益最大化,即g13=1,g23=1,g33=1。
(4)项目贡献度。假定全过程工程咨询项目出现紧急情况时,各参与方的贡献度相同,即投入的成本相同,则可得g14=1/3、g24=1/3、g34=1/3。
综上所述,上文通过相关模型等方法对风险分担、投入比重、合同履约度和项目贡献度4个因素进行参数确定,得到修正矩阵G。

3.2.2 修正Shapley值算法
(1)对修正矩阵G进行归一化处理,得到矩阵H。

(2)针对全过程工程咨询项目提出影响各成员利益分配的4个因素:风险分担、投入比重、合同履约度、项目贡献度,通过强制打分法确定其综合权重,确定利益分配影响系数P:
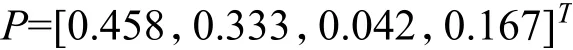
(3)由矩阵H和利益分配影响系数P,得到修正系数△K。
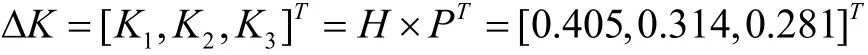
(4)根据式(3)得到修正后项目各成员的利益分配值为:
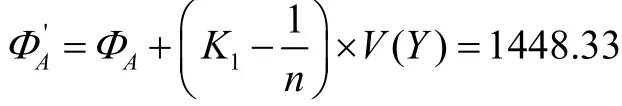
同理,可知B、C公司修正后的利益分配值分别为725.33万元和826.33万元。
3.3 基于Shapley值修正前后的利益分配值对比
通过修正后Shapley值得到全过程工程咨询项目在公司A、B、C之间最佳分配方案,即A、B、C公司利益分配值分别为1448.33万元、725.33万元、826.33万元,具体利益分配变化如表2所示,比较Shapley值修正前后项目参与方利益分配值发生明显变化,A公司增加了215万元,而B、C分别减少了58万元和157万元。这说明了A公司作为全过程工程咨询项目的牵头公司,投入的资源较多、风险分担比例较大,在考虑4个影响因素的基础上对其进行利益补偿,符合现实情况[15,16]。故而,修正后的Shapley值在联合体成员的利益分配方案上更加公平、公正、合理,同时调动了项目成员的积极性,也避免了项目实施过程中的非必要冲突,促使项目顺利完成[17,18]。
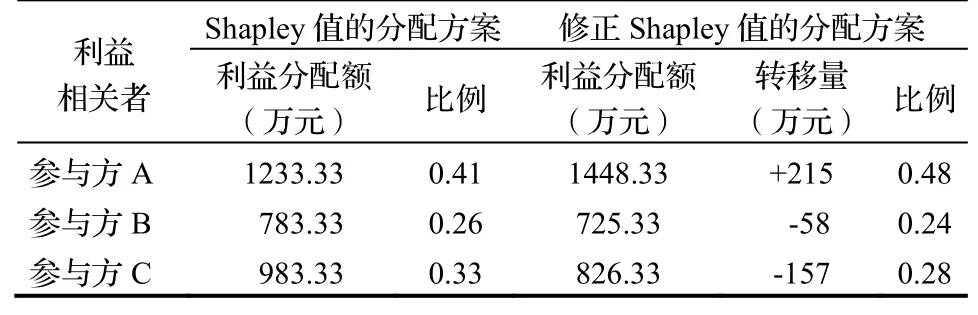
表2 Shapley 值修正前后项目参与方利益分配方案比较
4 结语
本文从全过程工程咨询项目联合体成员角度出发,探讨联合体成员之间的利益分配问题。通过建立Shapley值利益分配模型;引入4个影响全过程工程咨询项目利益分配的因素:风险分担、投入比重、合同履约度和项目贡献度;借助AHP、模糊综合评价及实际状况对全过程工程咨询项目的各影响因素进行权重修正,得到修正后的全过程工程咨询项目利益分配模型;通过高速公路全过程工程咨询项目案例进行计算,验证修正后Shapley值模型的可行性和有效性,使得利益分配结果更加公平、公正、合理,为全过程工程咨询项目利益分配方案提供了一种思路。然而,本文研究还有一些不足之处,在合同履约度和项目贡献度方面未进行深入研究,权重系数存在一定偏差,所以仍然需要优化全过程工程咨询联合体成员的利益分配方案,使联合体成员间的利益分配值精确化,这将是未来的研究方向。
