齿形襟翼结构尾缘轴流风机性能仿真研究

郑 楠， 叶学民， 杨天康， 李春曦

(华北电力大学 能源动力与机械工程学院，河北保定 071003)

大型轴流风机以体积流量大、高效率区宽等优势被广泛用于航空、能源和化工等领域，但运行中普遍存在能耗高、噪声大和结构振动等问题[1-2]。为此，国内外学者提出了表面开槽、增设端壁机匣、叶尖处理、叶片弯掠、尾缘襟翼、锯齿尾缘和尾缘吹气等多种主动流动控制措施[3-4]。

叶片结构特性是影响风机性能和气动噪声的重要因素之一。研究表明，增设尾缘襟翼可有效改善翼型的性能。Alber等[5]进行了风力机风洞实验，发现采用高度为0.5%c(c为弦长)和1%c的Gurney襟翼(GF)时，叶片升力系数可分别提升9.3%和16.9%。Chen等[6]研究了不同高度的GF对轴流风机性能的影响。Zhu等[7]分析了不同高度和宽度的GF对直叶片垂直轴风机性能的影响。Li等[8]模拟了GF对轴流风机性能、气动噪声及内流特征的影响。

另外，采用锯齿尾缘技术不仅降噪效果突出，而且其结构简单。叶学民等[9]研究了不同锯齿长度的尾缘对轴流风机气动噪声、压力及性能的影响，发现锯齿尾缘可明显降低轴流风机的中低频段噪声和流道中气流的压力脉动强度。Ryi等[10]通过风洞实验发现，采用直锯齿和斜锯齿尾缘叶片可降低风机气动噪声。仝帆等[11-12]基于数值计算阐述了锯齿尾缘的降噪机理，认为锯齿尾缘可抑制翼型的尾涡脱落、推迟边界层分离并降低流场的压力脉动，在反向对称涡的作用下涡结构快速破碎成小尺度涡，从而中低频段气动噪声得到明显抑制。

上述研究表明，增设尾缘襟翼在提升翼型性能方面具有一定的优势，但气动噪声会随之增大；基于仿生结构的锯齿尾缘在一定程度可降低气动噪声，但在某些工况下翼型的性能会有一定程度的降低。为此，笔者提出一种新型齿形襟翼结构，采用计算流体力学和计算气动声学的方法，分析该结构对某两级动叶可调轴流风机性能、气动噪声特性和内流结构的影响，探讨其影响机理，以期为风机的性能优化提供依据。

1 数值模拟

1.1 几何模型

图1为某两级动叶可调轴流风机模型示意图。计算区域由集流器、两级动叶、两级导叶和扩压器组成。动叶数为24，导叶数为23，两级动叶采用相同翼型，Ⅰ级导叶为等厚的复合式圆弧板，Ⅱ级导叶为相同长度的等厚圆弧板。动叶高度为295 mm，叶轮直径为1 778 mm，叶顶间隙为4.5 mm，转速为1 490 r/min，动叶中部弦长c为198 mm。设计工况点的体积流量为82.5 m3/s，全压为11.866 kPa，全压效率为88.3%。

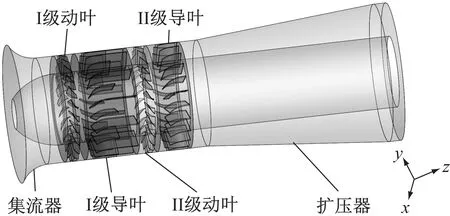
图1 风机模型示意图

为充分利用襟翼和齿形尾缘结构带来的不同优势，现提出一种新型尾缘结构，即在叶片尾缘处增设齿形襟翼，研究其结构及齿长对风机性能和气动噪声的影响。Bianchini等[13-15]的研究结果表明，高度为2%c的襟翼可显著提升翼型的性能。基于上述结果，拟在动叶尾缘加装垂直于翼弦的襟翼，其高度h和宽度b分别为2%c和0.5%c。取齿形襟翼的齿宽λ=7 mm，齿长l几何参数见表1。其中，方案1为常见的襟翼结构，其他方案为不同齿长的齿形襟翼结构。叶片模型示意图见图2。

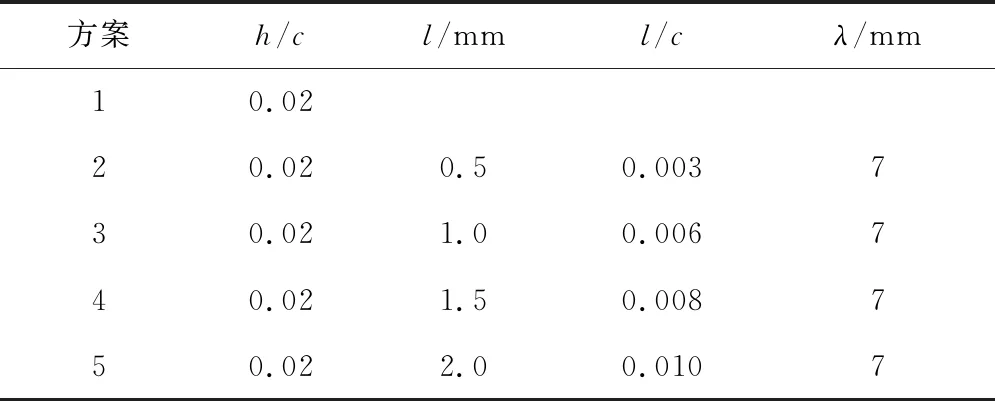
表1 齿形襟翼几何参数

(a) 原风机叶片

1.2 计算方法

采用Fluent多重参考系模型(MRF)对整机进行定常数值计算，选用带有旋转流动、二次流修正的Realizablek-ε湍流模型[2]。压力-速度耦合采用收敛性更好的SIMPLEC算法，动量方程中扩散项和对流项等选择二阶迎风离散格式。动、静交界面采用interface边界条件，以实现两交界面的数据传递。集流器入口设为速度边界条件，扩压器出口选择自由出流。当各项监视参数残差小于10-4且进出口截面的平均总压不变时，视计算已收敛。

为分析动叶区静压时域特征、噪声源分布和湍动能变化与齿长间的内在联系，将稳态计算结果作为大涡模拟(LES)计算的初场，选择压力-速度耦合的PISO算法，并采用精度较高的二阶隐式时间推进法进行气动噪声模拟[3]。动叶区流动结构复杂，能量变化剧烈且压力脉动显著，故选择动叶轮旋转域为噪声源面，在Ⅰ、Ⅱ级动叶尾缘25%、50%、75%叶高处的流道内设置具有代表性的监测点(M1～M6)，用于监测该区域的瞬时静压变化，监测点布置见图3。

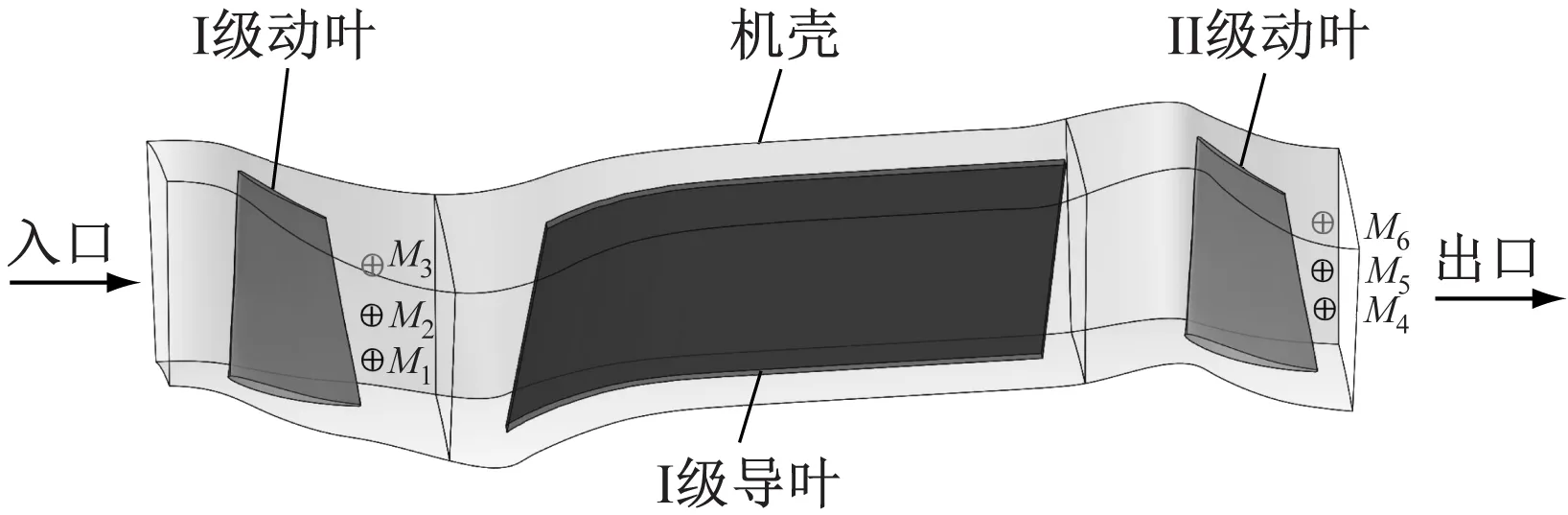
图3 监测点分布

1.3 网格划分及无关性验证

采用ICEM对动叶区和静叶区分别进行非结构、结构化网格划分，并对齿形区域进行网格加密，如图4所示。为评估网格数对模拟结果的影响，对原风机模型进行网格无关性验证，结果见表2。当网格数为1 010万时，继续增加网格数对计算精度的影响很小。因此，选择1 010万网格进行模拟，此时Ⅰ、Ⅱ级动叶区网格数分别为453万和451万。

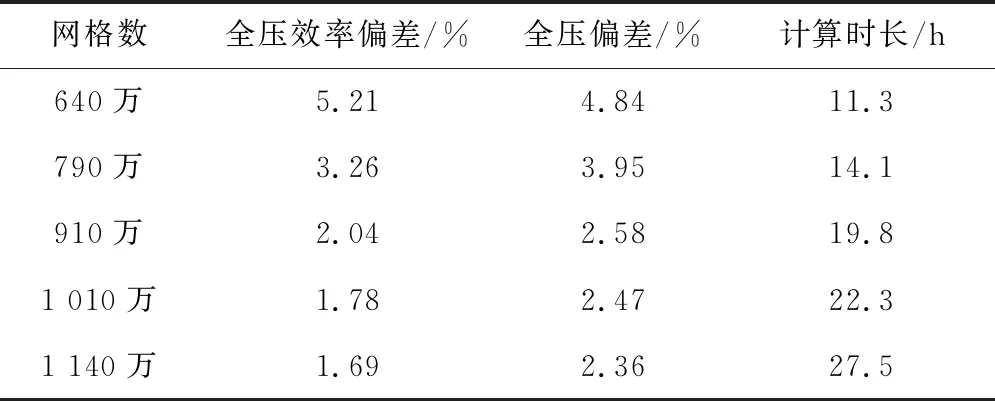
表2 网格无关性验证

(a) 整机网格

1.4 模拟结果验证

为验证模拟结果的准确性，在体积流量qV为80.0～92.5 m3/s范围内对风机全压Δp和全压效率η的模拟值与实验值进行对比，如图5所示。在设计体积流量qV,d为82.5 m3/s时，全压和全压效率模拟值与实验值间的偏差分别为0.66%和3.98%；在全体积流量范围内，全压平均偏差为0.77%，全压效率平均偏差低于3.3%。这表明所建模型、网格划分及所选模型均可满足计算要求，故模拟结果可准确反映风机的性能。

图5 全压和全压效率模拟值与实验值的对比

2 结果与分析

2.1 风机性能

图6为原风机和5种方案下风机全压和全压效率曲线。由图6可知，方案2～方案5在大体积流量侧均可显著提升风机全压和全压效率，且运行高效区较原风机明显变宽。由图6(a)可知，方案1～方案5均可在全体积流量范围内有效提高风机全压，设计体积流量qV,d为82.5 m3/s时，方案1～方案5下的全压较原风机分别提升14.74%、14.21%、12.87%、11.81%和11.03%，即随着齿长的减小，全压呈增大趋势。

由图6(b)可知，与原风机相比，方案1～方案5的风机全压效率在小体积流量侧有所下降，但在大体积流量侧提升幅度较大，且体积流量越大，全压效率提高越明显。同时，改型后风机的最大全压效率向大体积流量侧移动。当qV大于设计体积流量时，与原风机相比，方案4的风机全压效率增幅最大，其全压效率在qV为92.5 m3/s时较原风机提高1.71%。虽然方案1的全压提升最大，但其全压效率在较宽体积流量范围内均远低于原风机，而方案2～方案5在提高全压、改善大体积流量侧全压效率和拓宽运行高效区等综合性能方面表现更优。考虑到风机常在大体积流量、变工况条件下运行，故方案4为齿形襟翼结构尾缘改型的最佳方案。

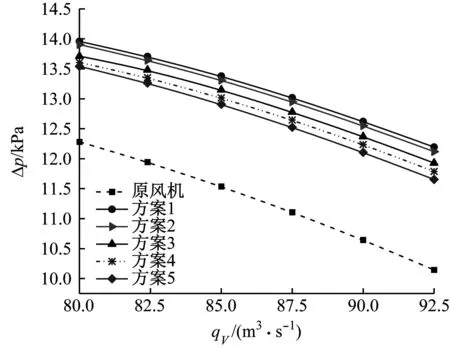
(a) 全压

2.2 时域分析

图7给出了设计体积流量下风机在1个旋转周期内监测点M1～M3的静压时域特性。由图7可知，不同齿长襟翼下各监测点的静压呈周期性变化，其波动周期约为0.001 68 s，波动频率为596 Hz，静压波动频率与叶片通过频率一致。这是由动叶旋转过程中周期性打击周围流体所致，与Shin等[16]所得到的非稳态压力变化规律相符。

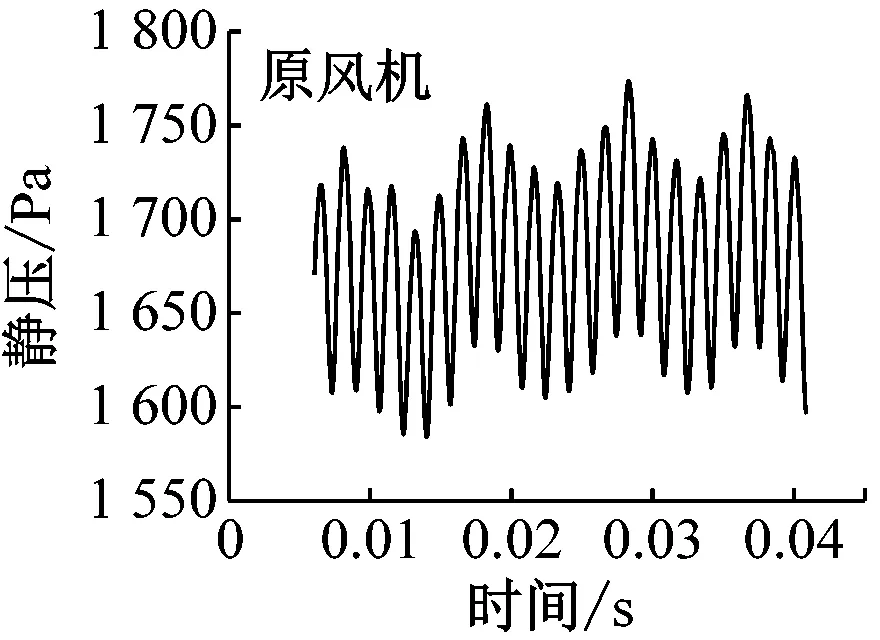
(a) M1

由图7可知，原风机的静压脉动频繁，静压峰值点脉动呈类似正弦波特征，方案1～方案5的静压脉动明显减缓，总体呈抛物线形。以监测点M1为例进行分析，原风机的静压均值为1 681 Pa，静压相邻峰值与谷值之差最大为146 Pa。采用方案1时静压最小谷值仍比原风机最大峰值高49 Pa。采用方案2～方案5时，静压均值随齿长增加呈先减小后增大的趋势，且其变化幅度随齿长的增加也有所增大，其中方案4的静压均值最小，较原风机减小402 Pa。同一方案下，静压均值沿叶高方向逐渐减小，Ⅱ级动叶区的静压均值沿叶高方向的分布规律与Ⅰ级动叶区一致。与原风机相比，5种方案的静压脉动明显减小，这有利于降低当地气动噪声；但另一方面，由于方案1的静压脉动幅度显著增大，致使当地噪声增大，而采用方案2～方案5后静压均值明显减小，尤其方案4的叶片静压均值降幅最大，因此对应的降噪效果最为显著。

2.3 噪声分布

图8为M1～M3处的声压级分布。由图8可知，在0～1 200 Hz频段内，各方案下气动噪声频谱无显著差异。当频率>1 200 Hz时，原风机声压级振荡较为明显，平均声压级为68 dB；方案1的声压级较原风机小幅增大，这与文献[17]中的研究结论一致；采用方案2～方案5后，高频气动噪声大幅下降，其中方案3和方案4的高频降噪最为显著，但方案3在倍频处气动噪声波动更加明显；方案2～方案5的气动噪声降低幅度沿叶高方向逐渐减小。

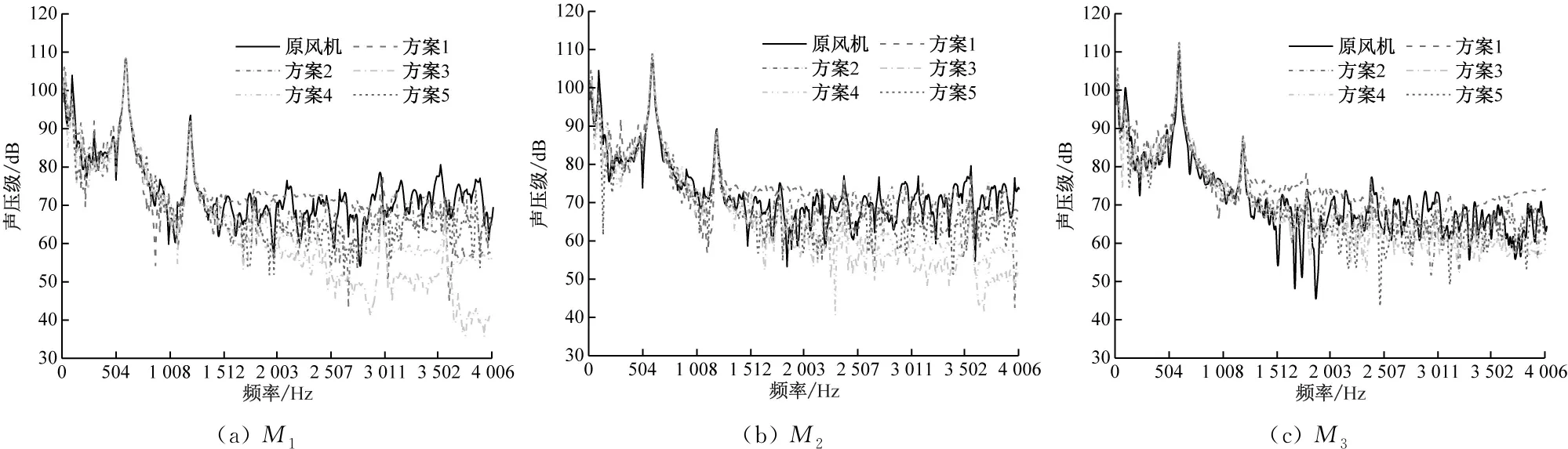
图8 不同方案下的声压级分布

2.4 噪声源分布

在气动声学中，静压时均值pRMS能清晰直观地反映出噪声源的位置和强度分布，其表达式为：

(1)

式中：pi为瞬时压力，Pa；t为时间，s；N为总采样数。

压力面(PS)前缘分离涡、尾缘脱落涡和叶顶泄漏涡在叶片吸力面(SS)对应位置形成较大的速度脉动和压力脉动，即噪声源主要分布在叶片吸力面前缘、尾缘和叶顶附近，故pRMS在叶片吸力面的变化更为显著[18]。

图9给出了Ⅰ级动叶区叶片吸力面pRMS的分布特征。由图9可知，不同齿长襟翼下噪声源呈现相似的分布特征，叶片尾缘顶部、叶根和叶顶中部发生剧烈的压力变化，为主要噪声源区。沿叶片后缘方向pRMS呈先增大后减小再增大的分布特点，这与Li等[18]得出的pRMS沿叶片尾缘方向减小的计算结果不同。其可能原因是本研究中动叶为安装角可调的大弯角扭叶片，叶顶泄漏涡与主流在叶顶中部附近相互汇合并发生作用，造成该区域速度和压力持续产生不规律的剧烈变化。在叶片尾缘顶部和叶根区域，由于尾迹涡不断交替脱落，发生强烈的尾涡分离，造成局部噪声源强度增大。由图9(b)可知，采用方案1时叶片做功能力增强，吸力面与压力面之间的压差增大，导致噪声源强度随局部叶顶泄漏涡强度的增大而增大，襟翼同时抑制了叶片流动边界层的分离[17]，且叶根处的泡状涡得到显著改善，该处噪声源强度降低。从图9(c)～图9(e)可以看出，相较于原风机，方案2～方案5的叶片叶顶区域噪声源强度随齿长的增加呈先增大后减小的趋势，叶根处分离涡强度减小，其分布区域也缩小，表现为高pRMS分布区域缩小，且方案4在叶顶及尾缘顶部pRMS增幅不大的前提下，大大降低了尾缘根部噪声源强度并减小了高噪声源强度分布区域。从图9(e)可以进一步看出，叶片尾缘顶部分离涡及叶顶中部泄漏流产生的压力变化仍是产生气动噪声的主要原因，因此下一步可同时优化锯齿分布及叶顶流动，进行深度降噪。

(a) 原风机

图10给出了设计体积流量下不同方案的最大静压时均值pRMSmax的变化。由图10可知，齿长对Ⅰ级动叶区pRMSmax的影响较小，但在Ⅱ级动叶区，pRMSmax随齿长的增大呈先增大后减小的趋势，且方案2下Ⅱ级动叶区的pRMSmax最大。其原因不仅是Ⅱ级动叶区的静压时均值高于Ⅰ级动叶区，且其流场比Ⅰ级动叶区更为复杂，方案4下Ⅰ、Ⅱ级动叶区的涡结构见图11。

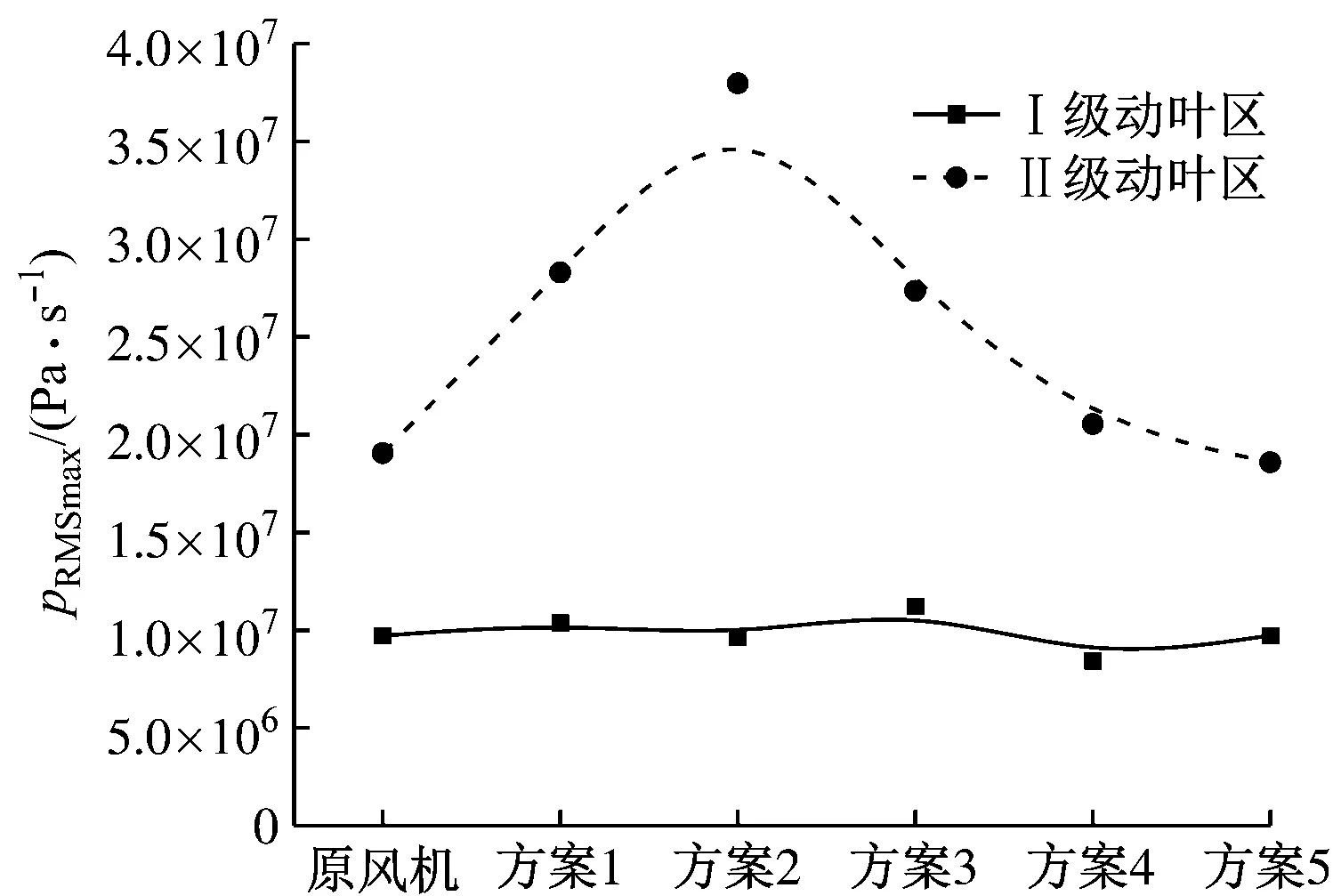
图10 不同方案下pRMSmax的变化

图11 方案4下Ⅰ、Ⅱ级动叶区的涡结构

2.5 湍流强度分布

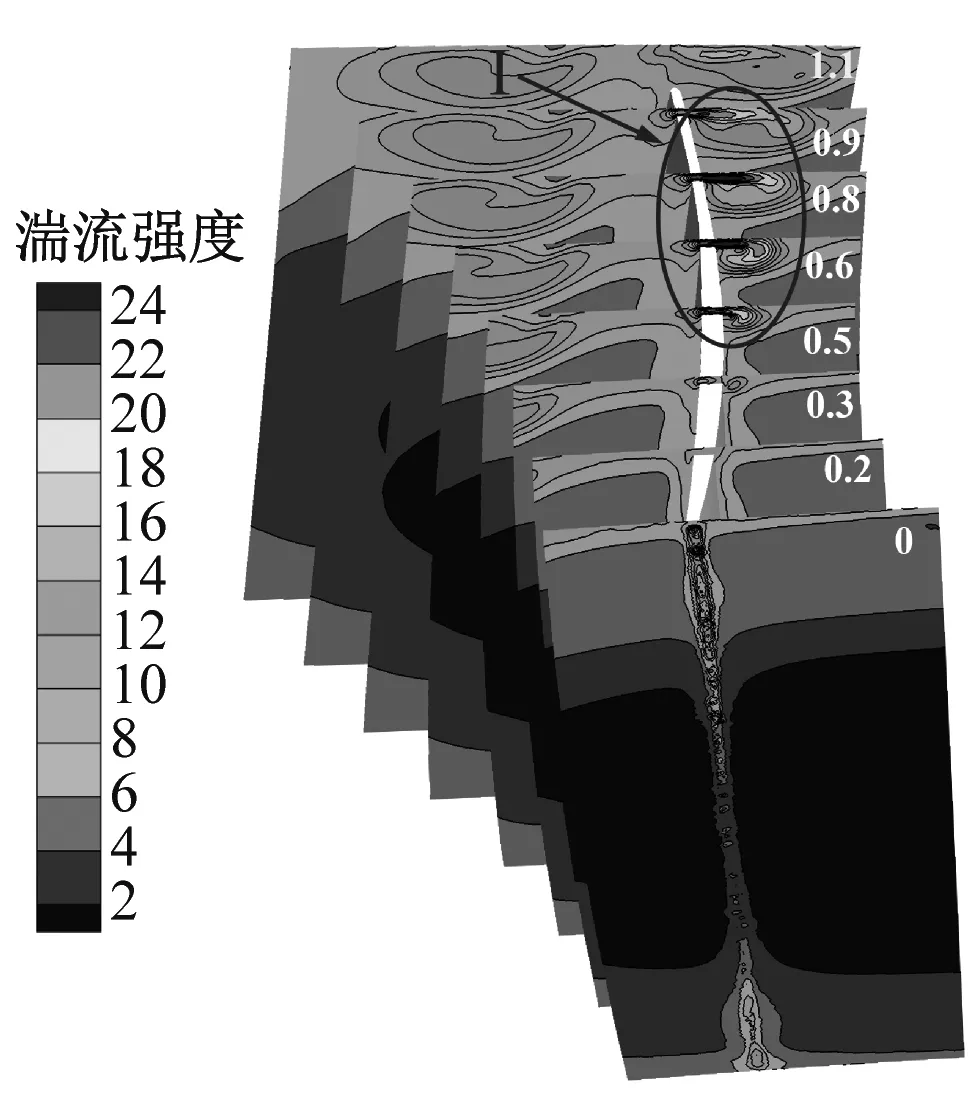
为进一步了解不同齿长襟翼对风机性能、内流结构和气动噪声影响的内在机理，图12给出了原风机、方案1和方案4在不同相对弦长cx位置截面上的湍流强度等值线分布。其中，cx=x/c1，x为截面距前缘的距离，c1为叶顶弦长。湍流强度ε为：

(2)

式中：u、v和w分别为x、y和z方向上的瞬时速度。

由图12(a)可知，原风机、方案1和方案4在cx=0.5～1.0范围内的湍流强度脉动较大，且该区域主要分布在吸力面侧，这与前文pRMS在叶片吸力面变化更为显著的结果一致。与原风机相比，方案4显著降低了叶片前缘分离涡和叶顶泄漏涡共同作用产生的湍流脉动强度。对比不同方案下cx=0处的湍流强度分布可知，方案4使叶片前缘分离涡数量减小，这对于降低叶片前缘的湍流强度也有一定的改善作用。

(a) 原风机

为详细说明湍流强度变化的内在原因，图13对比了3种方案下的涡结构。由图13(b)可知，采用方案1时，由于尾缘脱落涡绕过襟翼后自叶根向叶顶倾斜发展，在尾缘脱落涡和叶顶泄漏涡的共同作用下，湍流强度脉动由叶顶中部延伸至叶片尾缘的流道内，且叶片两侧的湍流强度分布并未得到明显改善，这是方案1叶片气动噪声提高的主要原因。方案4的齿形襟翼降低了尾缘附近的尾迹湍流强度，且减小了叶根泡状涡和尾迹涡的大小及分布。

(a) 原风机

2.6 降噪机理

Chong等[19]发现了锯齿尾缘反向对称涡的存在，认为在压力面与吸力面之间的压差作用下，压力面部分气流从锯齿间隙泄漏至吸力面，与吸力面气流掺混，在锯齿两侧的间隙生成流向相反的对称涡。Wang等[20]研究了波浪形前缘叶片吸力面齿顶、齿中和齿槽截面区域上的瞬时涡量分布，认为在波浪前缘流动分离处存在反向对称涡，且2个相邻涡旋的强烈相互作用使黏性耗散加快。图14给出了原风机和方案4中不同截面处的瞬时涡量分布。与原风机相比，方案4叶片尾缘处的流动发生显著变化，这表现为在锯齿前后存在压差和速度梯度，在锯齿尾缘处产生了一对垂直、旋向相反的涡(标记A)。这与杨景茹等[12]的研究结果相似，但与其发现的锯齿尾缘降噪机理相比，齿形襟翼尾缘降噪机理的不同之处在于在吸力面与压力面之间压差的作用下，齿形襟翼齿峰、齿中和齿槽截面内也产生了一对水平的反向对称涡(标记B)。为清晰说明水平反向对称涡的存在，图15给出了方案4齿峰截面处的流场示意图。

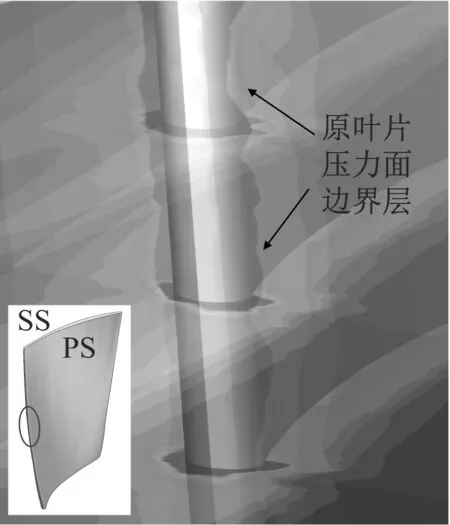
(a) 原风机

图15 方案4齿峰截面处的流场

综上可知，2对反向对称涡相互作用强烈，减小了附着涡和尾迹涡等非定常涡结构及所占区域面积，改变了齿形襟翼周围的湍流强度、涡量分布及涡脱落频率，能量耗散加快，有利于抑制黏性应力辐射的四极子噪声[21]，这是齿形襟翼结构尾缘能降噪的主要原因。

3 结 论

(1) 齿形襟翼结构可显著提高风机的性能，且全压增幅与齿长成反比，4种齿长在全体积流量范围内平均增幅为12.93%；增设齿形襟翼后，风机全压效率最高点向大体积流量侧移动，运行高效区变宽，但在小体积流量侧全压效率稍有下降。

(2) 与原风机相比，齿形襟翼叶片静压均值随齿长的增大呈先减小后增大的趋势，其中方案4的静压均值最小，较原风机降低402 Pa，高频气动噪声显著降低；齿形襟翼叶片尾缘顶部和叶顶区域噪声源强度随齿长的增大先增大后减小，叶根处分离涡强度减小，其分布区域也缩小，且方案4叶片在叶顶pRMS增幅不大的前提下，尾缘根部噪声源强度及分布区域显著减小，在改善全压效率、全压和降噪方面方案4的综合性能最优。

(3) 齿形襟翼使叶片前缘分离涡和叶顶泄漏涡共同作用产生的湍流脉动强度降低，减小了尾迹涡大小及其分布区域，对叶片前缘的湍流强度也有一定的改善作用；在锯齿前后压差以及吸力面与压力面之间压差的作用下，产生了2对反向对称涡，其相互作用强烈，能量耗散加快，这是齿形襟翼结构尾缘能降噪的主要原因。