流量在线测验垂线布设方案探析
——以前垾村水文站为例
2022-05-18单延功张维东谢海文朱庆云韩伯成朱永军
单延功,张维东,谢海文,朱庆云,韩伯成,朱永军
(江苏省水文水资源勘测局南京分局,江苏 南京 210008)
1 概 述
秦淮河位于长江南京段南岸,由发源于句容境内的句容河和发源于溧水县境内的溧水河在江宁区境内汇合而成。句容河是秦淮河最大的支流,前垾村(句)水文站为句容河控制站,该站于1953年设立,2009年5月因下游建桥影响,测流断面往上游迁移60 m,与基本水尺断面重合。
对于坐底式ADCP 在线流量测验方案而言,其关键是要确定仪器在测验断面上的安装位置。由于设备价格和实际安装存在困难等因素,不可能在河床每根垂线位置上安装1 台仪器,所以有必要对常测法测速垂线进行精简分析,只保留1 根或2 根垂线作为在线流速测验的垂线。
《声学多普勒流量测验规范》(SL 337—2006)规定,垂向代表线法流量测验采用的代表线数目及位置应通过比测、分析确定[1]。《水文测验手册》规定,没有精测资料的测站,可用常测法资料分析,如精度符合规定(即累积频率达75%以上的误差不超过±4%,累积频率达95%以上的误差不超过±8%),可作为简测法使用[2]。本文根据上述规范要求,选用新测流断面启用后的2009—2016年共计288 次常测法流量测验资料,利用Matlab 软件编写多元回归程序,分析垂线流速与断面平均流速之间的关系,确定代表垂线位置并以此作为坐底式ADCP 流速仪的安装位置。
2 相关资料与分析方法
2.1 测验断面基本情况
选用资料为288 次常测法流量资料,测验时间为2009—2016年,所选择的资料质量可靠,精度较高,且分布在低、中、高各级水位,具有代表性。
前垾村(句)断面呈U 形状,断面处河床基本顺直,断面稳定,主河宽128 m,架设过河测流电动缆道,历年采用流速仪法常测法测流,8 根测速垂线(起点距分别为13.2 m、30.0 m、50.0 m、65.0 m、77.0 m、90.0 m、105 m、120 m),采用二点法测速。
分析选用的4条垂线起点距分别为50 m、65 m、77 m和90 m,处于河道主泓区。
2.2 分析方法
2.2.1 多元线性回归
多元线性回归模型[3]的一般形式为
式中,k为解释变量的数目,βj(j=1,2,…,k)为回归系数。
式(1)也被称为总体回归函数的随机表达式,非随机表达式为
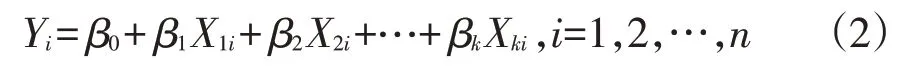
式中,βj为偏回归系数。
2.2.2 Matlab多元线性回归的实现
多元线性回归在Matlab中主要实现方法如下:
利用函数[b,bint,r,rint,stats]=regress(Y,X)确定回归系数的点估计值,其中输入参数X为1 与自变量组成的矩阵,表达式为
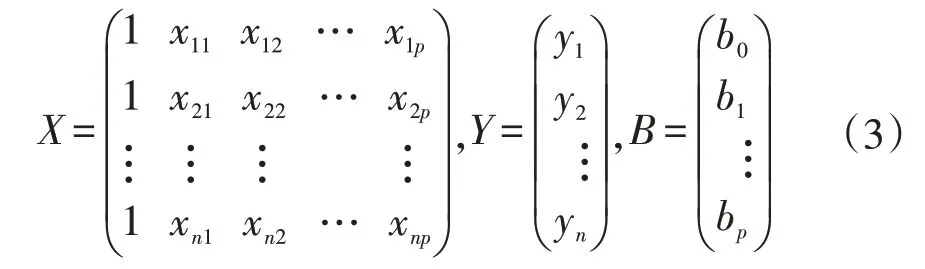
式中:输入参数Y为因变量的列向量,显著性水平ɑ默认值为0.05;输出参数b为回归系数,bint为b的置信区间,r为残差(列向量),rint为r的置信区间;stats包括3 个统计量,决定系数R2、F值、F(1,n-2)分布大于F值的概率p,p<ɑ时回归模型有效。
相关系数R2越接近1,说明回归方程越显著,F>F1-α(p,n-p-1)时拒绝H0;F越大,说明回归方程越显著,与F对应的概率p<α时拒绝H0,回归模型成立。
2.3 回归模型检验
首先,利用Matlab 提供的Lillietest 函数进行正态性检验;其次,利用Matlab 提供的Vartest 函数进行方差齐性检验;最后,利用Matlab提供的Dwtest函数进行自相关性检验。Durbin-Watson 统计量值介于0~4之间,统计量值为2时,数据完全不存在自相关性,越是接近0 或者4,说明数据之间的关联性越强。一般认为,统计量值介于1~3之间时,数据独立性不存在问题[4]。
3 分析结果
3.1 断面稳定性分析
根据2009—2016年实测大断面资料绘制大断面图,大断面高中低水位面积计算结果表明,各年断面面积变化小于±3%,符合规范规定的断面稳定要求。这一结果表明,所选用的流量资料的断面面积是一致的。
3.2 各垂线流速与断面平均流速关系
利用选用的4条测速垂线流速分别与断面平均流速绘制散点图,结果表明,各垂线流速与断面平均流速存在明显的线性关系,可以利用线性回归进行分析。
3.3 单根垂线与断面平均流速回归结果
分别利用各垂线流速与断面平均流速进行回归分析,计算累积频率75%以上的随机误差和累积频率95%以上的随机误差如表1。
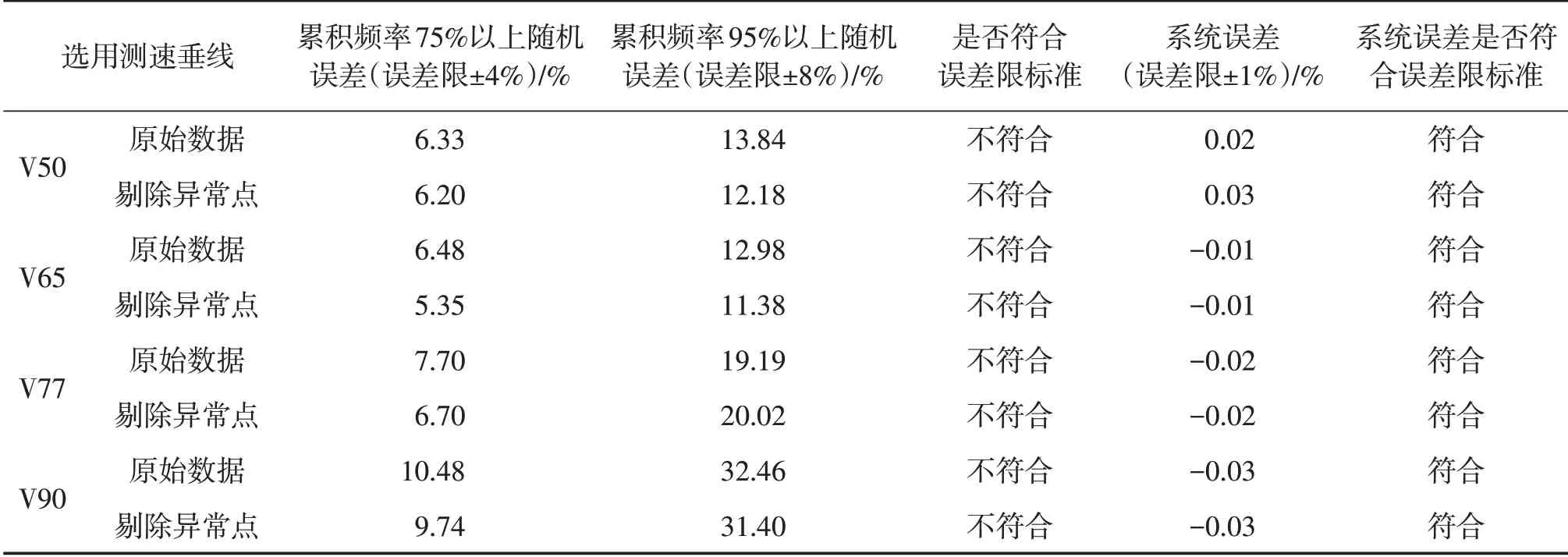
表1 单根垂线精简分析误差统计
分析结果表明,各垂线流速与断面平均流速相关关系都不符合误差限要求,在剔除了残差置信区间不含有0 的异常点后再次回归,随机误差依然不符合要求,无法用1根垂线作为代表线测速。
3.4 2根垂线与断面平均流速回归结果
分别利用2根垂线流速与断面平均流速进行回归分析,计算累积频率75%以上的随机误差和累积频率95%以上的随机误差如表2。
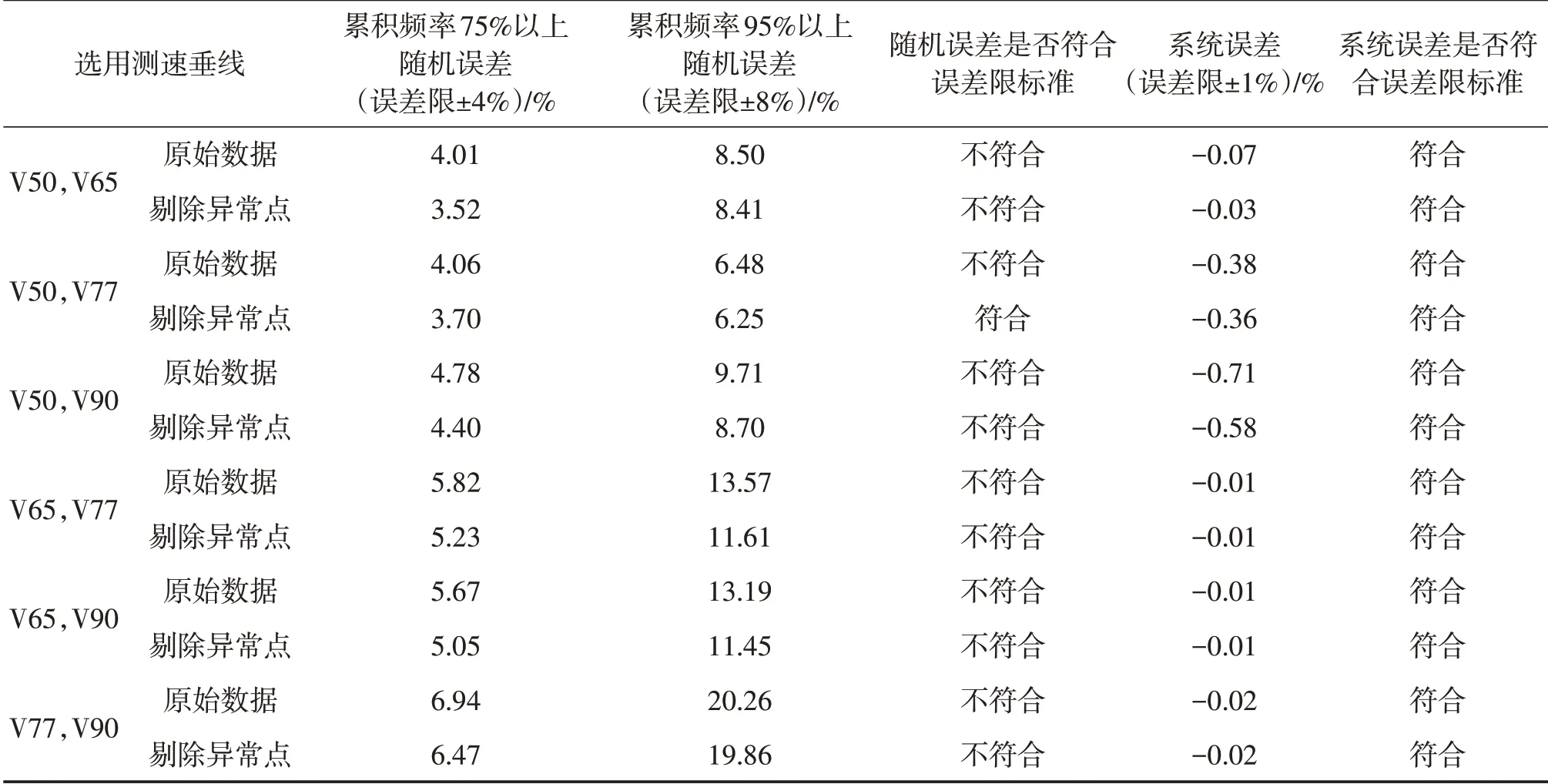
表2 2根垂线精简分析误差统计
分析结果表明,剔除残差置信区间不含有0 的异常点后,垂线V50 和V77 流速与断面平均流速回归的累积频率75%以上的随机误差和累积频率95%以上的随机误差符合误差限要求,可以利用垂线V50和V77作为代表线进行流速测验。
3.5 垂线V50和V77流速与断面平均流速回归结果
通过模型求解所得的回归结果如表3。
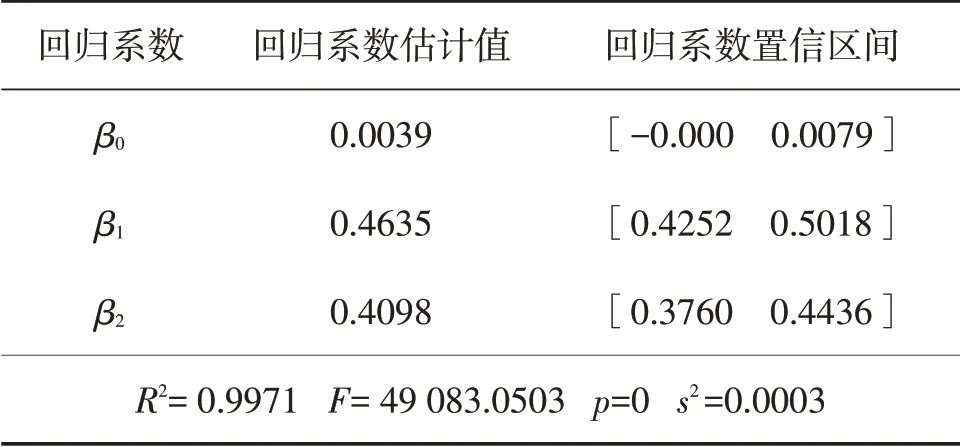
表3 回归结果
剔除残差置信区间不含0的异常点后得到回归结果如表4。
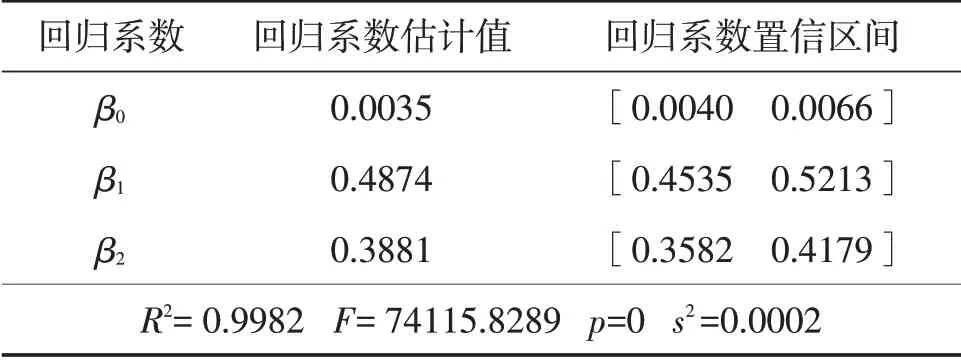
表4 剔除异常点回归结果
模型检验p值为0,说明模型通过检验。
根据回归结果,可以确定断面平均流速与垂线流速关系模型为:
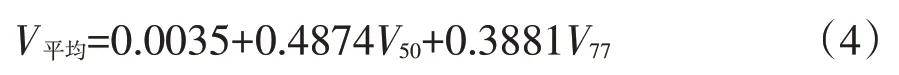
3.6 残差检验
V50和V77垂线流速与断面平均流速回归残差散点图如图1。
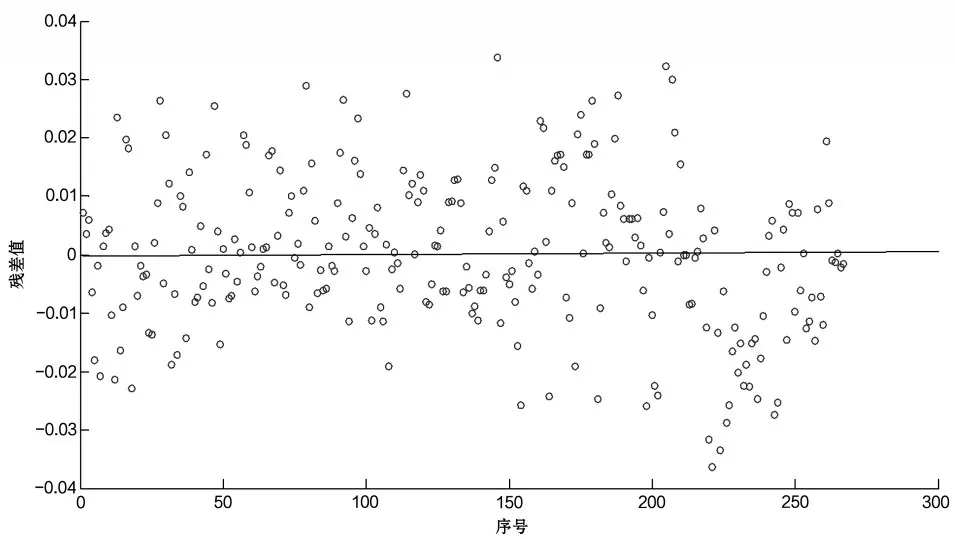
图1 残差散点分布
残差散点图显示,残差在0附近随机分布,无明显趋势。
残差检验结果如表5。

表5 残差检验结果
残差检验结果表明,数据在正态性、方差齐性和独立性方面都符合多元线性回归的适用条件。同时,本分析使用数据量远远超过《水文测验手册》规定的最低限值30,可以判定回归模型有效。
4 结 论
(1)单根垂线的流速与断面平均流速相关关系模型的随机误差均不满足规范规定的累积频率75%以上(误差限±4%)累积频率95%以上(误差限±8%)误差要求,而系统误差满足规范要求(误差限±1%)。
(2)2 根垂线的流速与断面平均流速相关关系模型的随机误差,只有V50 和V77 满足规范规定的累积频率75%以上(误差限±4%)累积频率95%以上(误差限±8%)误差要求,系统误差也满足规范要求(误差限±1%)。
(3)该站可以在V50 和V77 垂线处安装坐底式ADCP进行流量在线测验。
