一种混合结构柔性臂的轨迹跟踪控制器设计

宋艳东 胡海东 秦 岭 范 普

(内蒙古科技大学 信息工程学院，内蒙古 包头 014010)

1 混合结构柔性臂建模

1.1 假设模态法描述柔性形变

本文中，将所有连杆均视为Euler-Bernoulli 梁。根据假设模态法[1]，柔性偏差可表示为：

其中，φ (x)为模态函数，q(t)为模态坐标。

由于混合结构柔性臂由两节连杆嵌套组成，因此将连杆分为固定段、重叠段和延伸段建立坐标系，如图1所示。

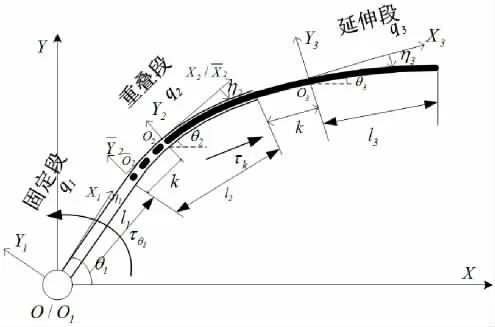
图1 混合结构柔性臂坐标系模型

由于混合结构柔性机械臂系统模型比较复杂且耦合程度高，因此本文将系统状态变量分为刚性结构变量u0和柔性结构变量u2[2]。其表达式分别为：

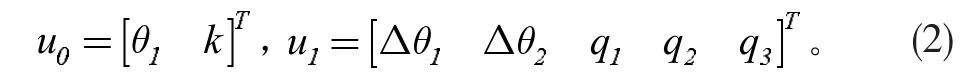
1.2 刚性结构部分建模

由刚体拉格朗日平衡方程[3]，可推导混合结构柔性机械臂刚性结构部分动力学方程为：

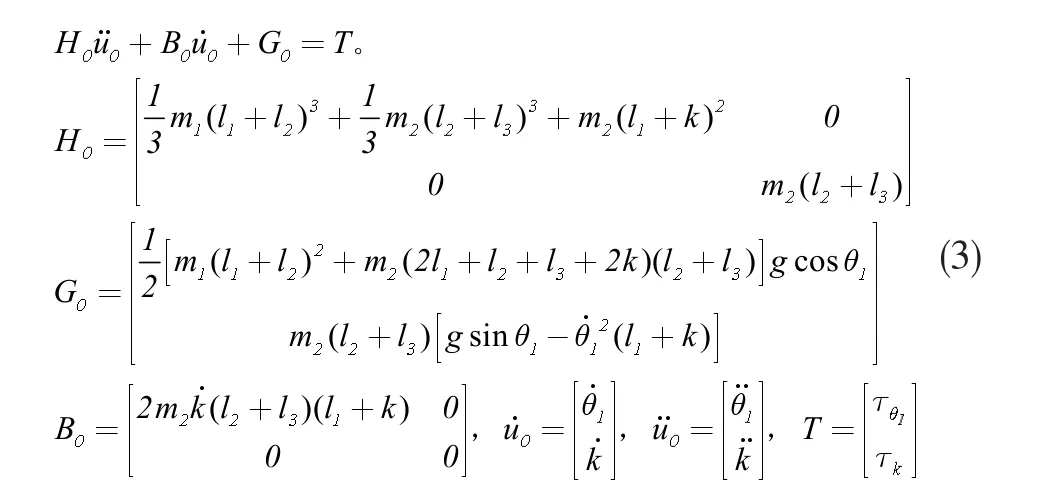
1.3 柔性结构部分建模

当考虑混合结构柔性机械臂的挠曲变形时，连杆上任意一点p 的位置矢量表示为：

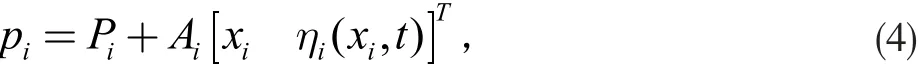
其中，Pi为该点所在参考坐标系原点在基坐标系中的位置向量；Ai为该点所在参考系坐标系到基坐标系的转换矩阵；ηi表示该点的柔性偏差。

由于 Δθ1, Δθ2为微小的柔性偏差角度，所以忽略二阶及以上的项，则p 点速度表达式为：

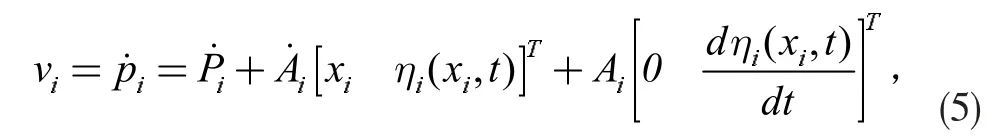
则系统动能表示为：

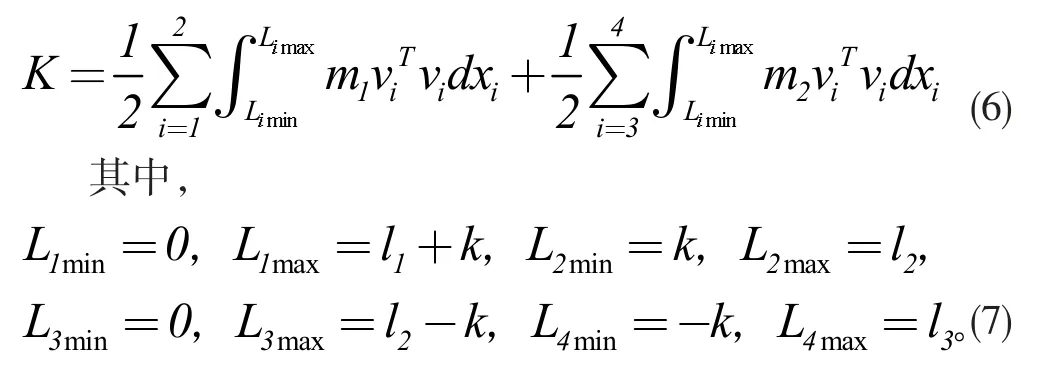
对于p 点的势能，依据动能计算方法，可表示为：

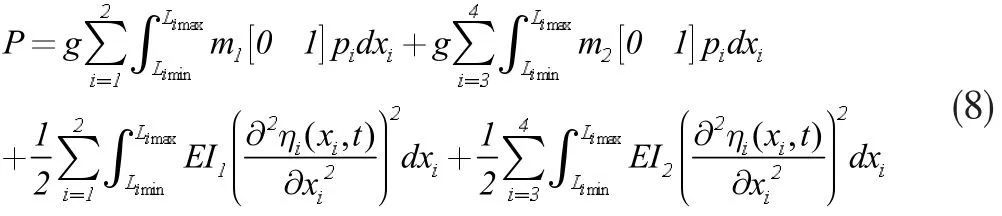
采用拉格朗日方程[4]，

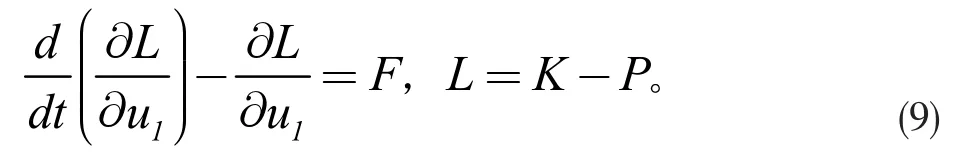
将式(6)和(8)代入式(9)，即可得柔性偏差部分动力学方程为：

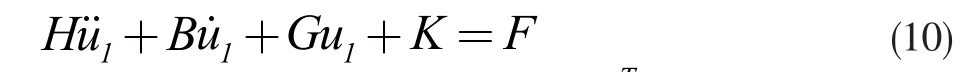
其中，F=［f1f 200 0］T◦对于上式，参数H,B,G,K都是关于刚性关节变量 θ1和k的函数，则方程(10)可视为一个线性时变系统。

2 轨迹跟踪控制器设计

混合结构柔性臂轨迹跟踪控制器的总体设计思路为给定参考轨迹，将滑模控制器控制力矩，输入到刚性结构部分动力学模型中得到刚性关节变量的运动轨迹，然后将实际运动轨迹与参考轨迹的偏差反馈至滑模控制器中形成闭环控制链。将刚性关节变量输入到柔性结构部分线性动力学方程中进行求解，即可得到柔性结构状态变量的变化情况。

2.1 滑模控制器的设计

定义Lyapunov 函数

则

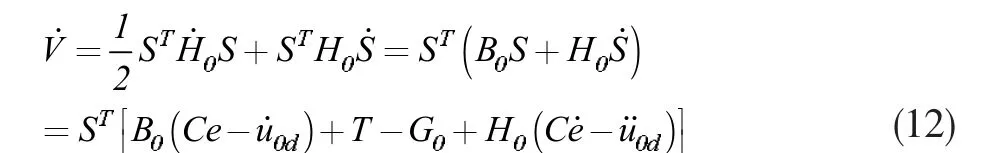
设计控制律为

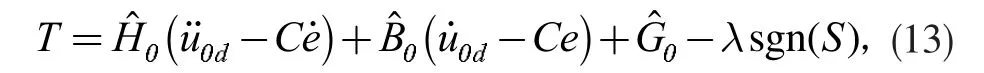
于是

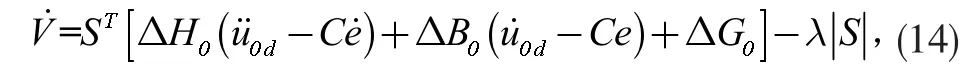
令

2.2 通过BLF 方法对部分输出变量施加约束

定义输出偏差为

定义Barrier Lyapunov 函数

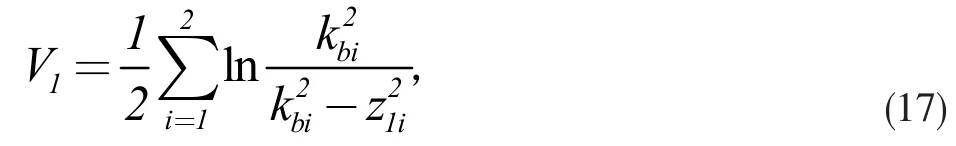
则

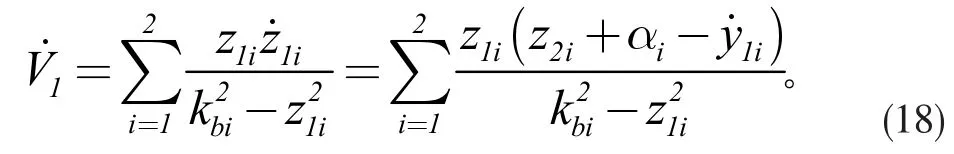
设计稳定函数

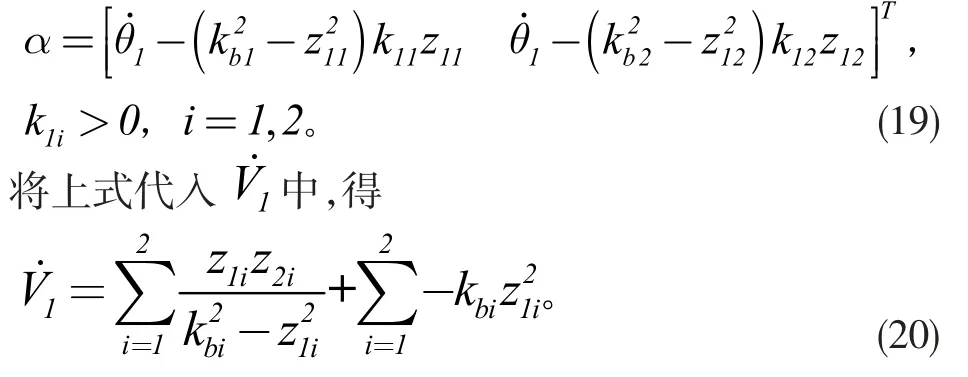
(2)定义Lyapunov 函数

对时间T 求导并结合式(10)、(20)，有：

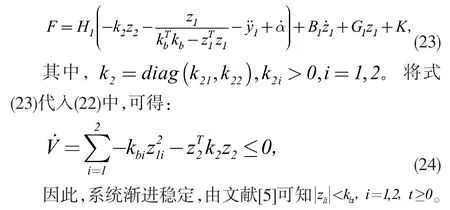
3 仿真结果

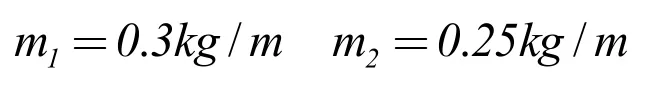
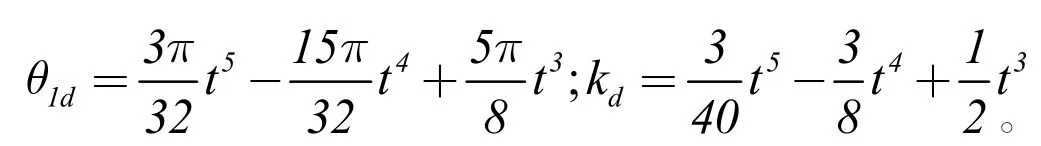
两关节变量初始状态为：θ1=0.06rad,k=0.02m，仿真时长为6s。仿真结果如图2 所示。

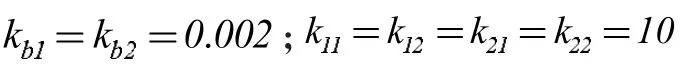
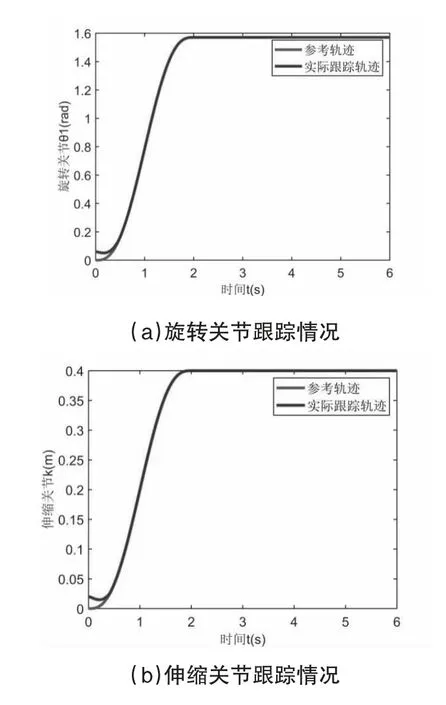
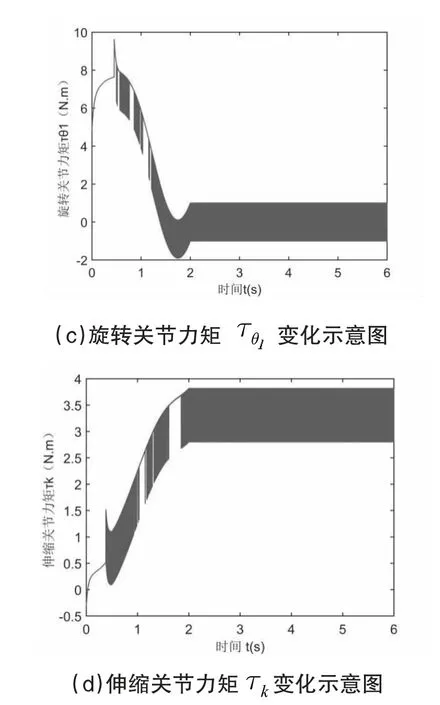
图2 旋转关节与伸缩关节轨迹跟踪与力矩变化示意图

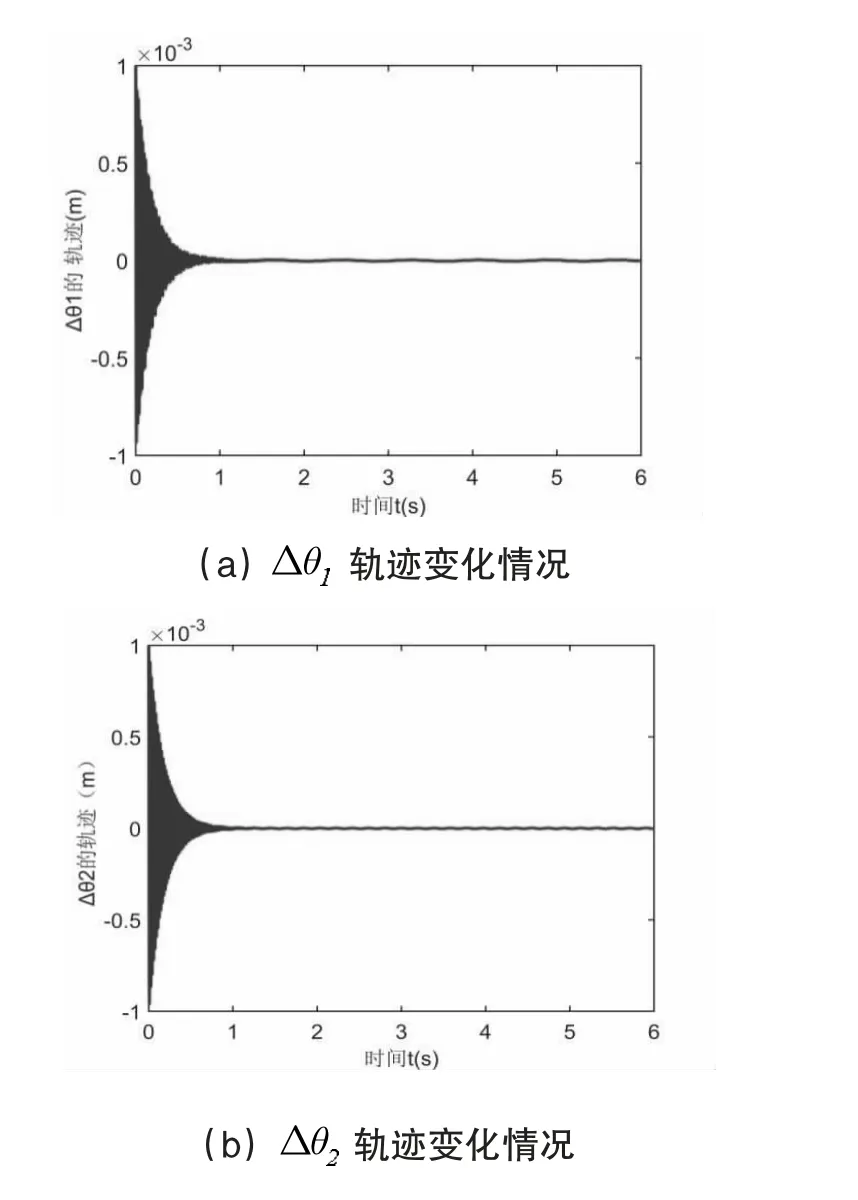
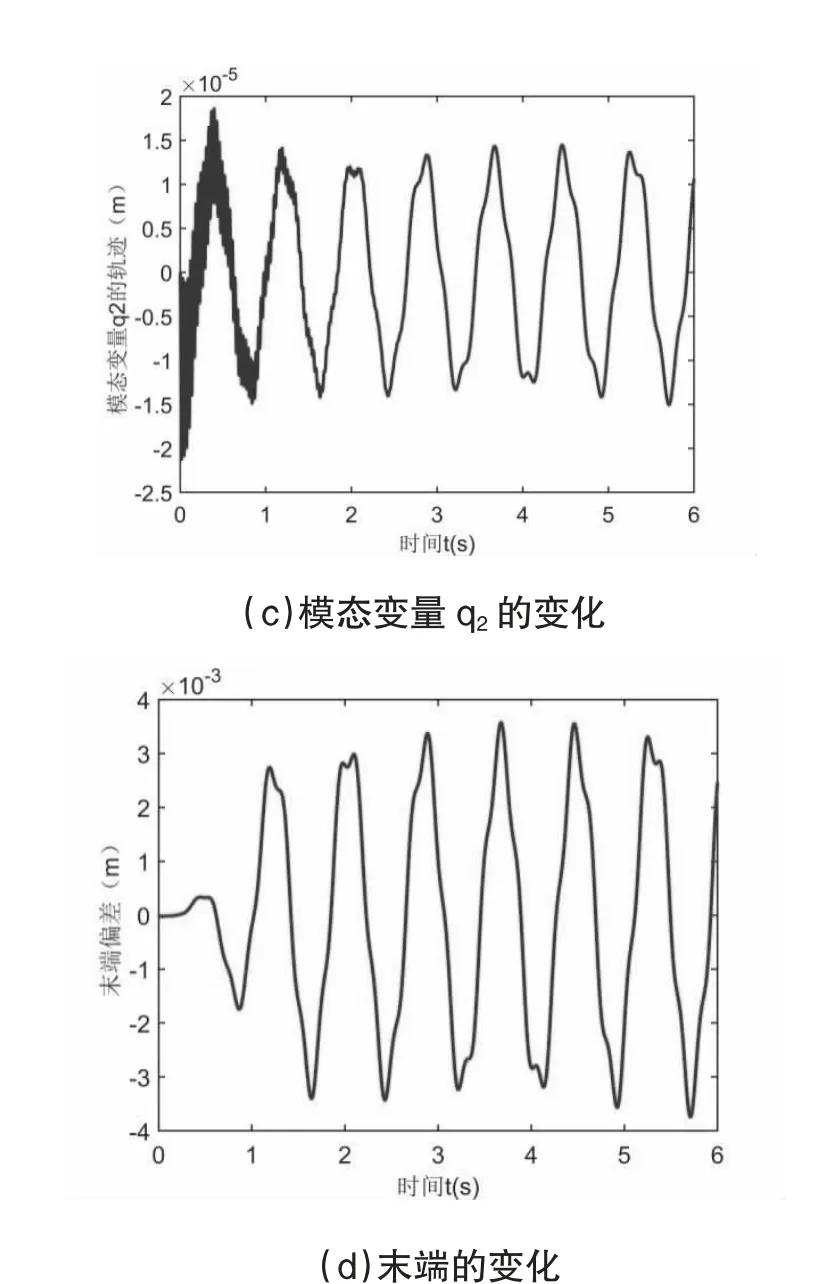
图3 柔性角度偏差 Δ Δ、模态变量q2 及末端随时间的变化

4 结论

本文针对混合结构柔性臂的结构特点，将系统分为固定段、重叠段、延伸段，并将系统分解为刚性部分和柔性部分分别进行建模。设计滑模控制器对刚性关节轨迹进行跟踪，并针对控制过程中出现柔性偏差角度变大的问题，采用Barrier Lyapunov 函数结合反演的方法，实现对柔性偏差角度的输出约束。