最小体积和平滑性约束的非负矩阵分解高光谱解混算法
2022-05-18李登刚
李登刚 李 洁
(湖南工业大学 轨道交通学院, 湖南 株洲 412007)
0 引言
近年来,卫星以及遥感技术得到了突飞猛进的发展,高光谱图像因其具有大量的光谱波段数,得到了广泛的关注。高光谱图像目前已经广泛应用在了农业监督、矿物挖掘、军事勘测等领域。但是由于卫星成像传感器空间分辨率的限制,真实的高光谱图像场景中往往存在着大量的混合像元。所谓混合像元,是指高光谱图像中单个像素包含了多种实际地物。混合像元的存在,将严重影响和制约后续对高光谱图像的处理与分析。为此,混合像元分解技术随之而生。混合像元分解(解混)就是把混合的像元分解为各个物质(称之为端元)及其对应所占的比例(称之为丰度)[1-3]。
近来,关于混合像元分解的方法层出不穷,总的来看,可以把这些分解方法分为两类。第一类,两步法(two step methods,TSM);第二类,一步法(single step methods,SSM)。两步法首先从混合像元中提取出各个物质端元,然后反演计算出各端元所对应的丰度。常用的端元提取算法有顶点成分分析法[4](vertex component analysis,VCA)、纯像素指数[5](pure pixel index,PPI)、N-FINDR[6]等。提取出端元后,通常通过全约束的最小二乘法[7](fully constrained least squares,FCLS)来反演求解出丰度。一步法可以同时计算出端元和丰度,传统的一步法包括独立成分分析法[8](independent component analysis,ICA)、最小体积约束的非负矩阵分解法[9](minimum volume constrained nonnegative matrix factorization,MVCNMF)等。
通过上述分析可以发现,对于两步法,如果在第一步端元提取中存在误差,那么第二步丰度反演中的累计误差将会继续变大。所以,同两步法相比,一步法可以很好地避免这个问题。此外,在真实的高光谱图像中,是否存在纯净像元是未知的。所以,那些需要原始高光谱图像中存在纯净像元的算法比如VCA、N-FINDR等并不适用。为了解决上述问题,混合像元盲分解问题随之而出。所谓盲分解,是指原始高光谱图像中,是否存在纯净像元,以及端元的个数都是未知的。非负矩阵分解(nonnegative matrix factorization,NMF)最初应用在数据降维,近年来被推广应用到了高光谱图像解混等领域。MVCNMF利用了混合像元的几何特征,将混合像元构成单形体的体积作为约束项加入到了目标函数的罚函数中。然而这一方法仅考虑了端元的物理属性,忽略了丰度相关特性。平滑性约束很好地利用了丰度向量之间的一致性[10],成功地利用了丰度的特征,将丰度的平滑性约束作为罚函数添加到目标函数中。然而,该方法忽略了端元相关的物理属性。
本文利用了高光谱图像端元和丰度的相关物理属性。首先,根据端元的几何特征,将混合像元中端元所构成单形体的体积作为约束项添加到了目标函数中。其次,充分利用了丰度的平滑性,通过构造平滑性约束项,将该约束项也加入到了目标函数中。与传统方法相比,本文既考虑到了端元的特性,同时又考虑到了丰度的相关物理属性。通过在非负矩阵分解的目标函数中结合体积约束和平滑性约束,提高了混合像元分解的分解精度等问题。
1 高光谱图像解混与非负矩阵分解
1.1线性混合模型
线性混合模型(linear mixed model,LMM)目前广泛应用在高光谱图像混合像元分解中[9-10],其数学模型定义为
X=AS+N
(1)
式中,矩阵X∈Rn×m表示传感器观测到的高光谱图像;矩阵A∈Rn×l表示端元;矩阵S∈Rl×m表示端元所对应的丰度;N表示可能出现的噪声和误差。

1.2 非负矩阵分解
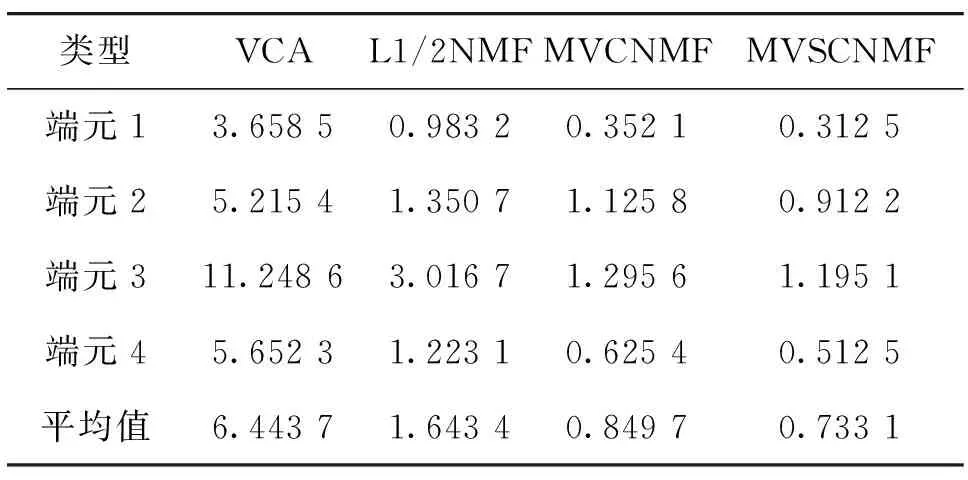
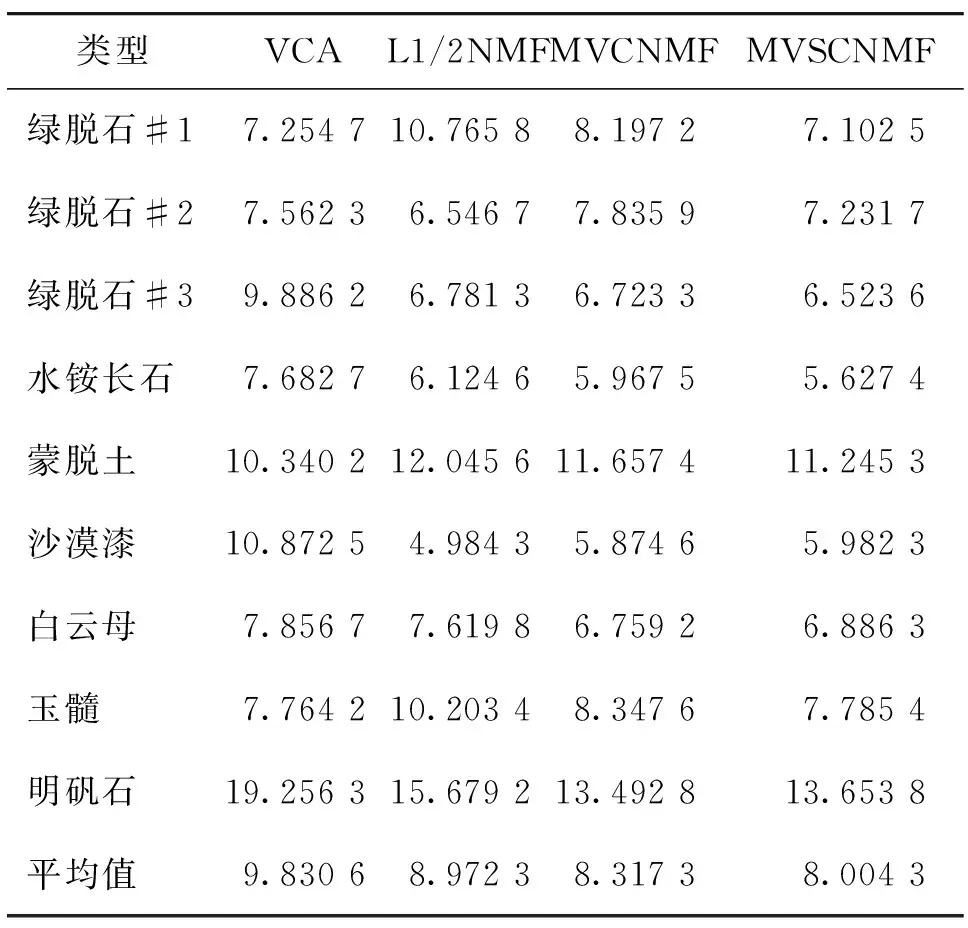
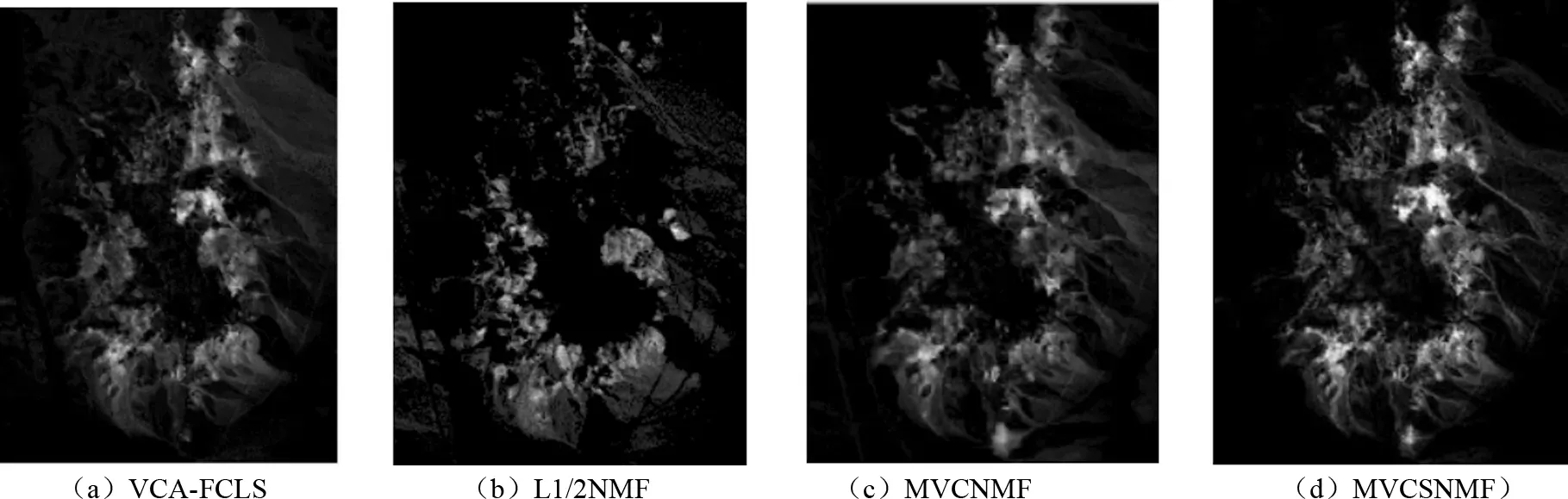
1999年,LEE D和SEUNG S提出了非负矩阵分解[11]理论。近年来,非负矩阵分解已成功应用到了数据降维、文本聚类、人脸识别等领域。对于非负矩阵Y∈Rn×m及常数r Y=WH (2) 使用欧式距离来定义Y与WH之间的误差,则目标函数可以表示为 (3) MVCNMF是一种典型的利用端元物理特性在目标函数中添加约束项的方法。该方法通过将混合像元所构成单形体的体积最小化。目标函数定义为: (4) 式中,vol(J(A))表示单形体的体积,由端元矩阵决定。MVCNMF有效地利用了端元矩阵相关属性,并对目标函数进行了有效的约束,但是这一方法忽略了丰度的相关特性。 正如文献[11]所述,平滑性用来描述相邻丰度向量之间的一致性,其也是丰度向量的一种物理属性。平滑性考虑的是地物本身在空间中分布具有的连续性,可以使混合像元分解的结果更加平滑,同时也可以增加地物在局部空间的主导性。参考文献[11],平滑性约束项的定义为 (5) (6) 若相邻像元在数据特征空间中越相似,那么该像元间的丰度也就会越相近。采用文献[11]中的8领域的结构,同时根据高斯核函数计算ui,j,可得 ui,j=e-‖x(i)-x(j)‖2 (7) 对公式(5)所述的平滑性约束性求梯度,可得 (8) 式中,S为丰度矩阵,矩阵Q和U定义见公式(6)。 针对传统非负矩阵分解方法分解精度不高等问题,本文结合了最小体积约束和平滑性约束,通过构造最小体积约束和平滑性约束的罚函数项,并将它们同时添加到了目标函数中,提出了基于最小体积约束和平滑性约束的非负矩阵分解算法(minimum volume and smooth constrained nonnegative matrix factorization,MVSCNMF)。MVSCNMF的目标函数定义为 (9) 接下来的问题为目标函数的求解,使用交替迭代更新算法来求解端元矩阵和丰度矩阵,即固定一个矩阵交替迭代求解另外一个矩阵,其数学模型为 (10) 利用梯度下降法,上述公式可以转换为 (11) MVSCNMF总结如下: 为了验证本文算法的准确性和有效性,分别用合成的模拟图像和真实的高光谱场景图像进行了实验。实验之前,首先提出比较各算法性能的评价指标。参考文献[9-10,12-15],采用光谱角距离(spectral angle distance,SAD)来评价分解出的端元和真实端元之间的相似性。SAD的定义为 (12) 从美国地质勘测局的光谱资源库中随机选取了4种端元来合成模拟的高光谱图像。所选取的光谱包含了224个波段,波长范围从0.38 μm到2.5 μm。合成的模拟图像拥有64×64个像素,然后被分成8×8个小像素块,每个小像素块都拥有纯净像元。使用一个7×7的滤波器来生成模拟的混合像元,为了进一步确保模拟图像中无纯净像元,对于那些丰度大于0.8的像素,用上述4种端元均匀构成的像元替代。最后,为了模拟可能出现的误差,通过向模拟图像添加信噪比SNR=20 dB的零均值高斯噪音来实现。表1列出了新提出的MVSCNMF与其他几种流行的解混方法的分解效果对比。 表1 模拟实验中不同方法下SAD值比较 从表1可以看出,VCA算法在所有的算法中提取端元的效果最差,这是因为VCA是从高光谱图像中提取纯净端元,而模拟图像中是不存在纯净像元的,所以VCA算法分解效果最差。同时,NMF是一种盲分解算法,不需要原图像中存在纯净像元,所以基于NMF的算法分解效果比VCA都要好。最后比较MVCNMF、L1/2NMF以及新提出的MVSCNMF发现,新提出的方法分解效果最好。这是因为,其他方法仅考虑了端元或者丰度的相关特性,而本文新提出的方法很好地利用了端元和丰度的相关物理特性,可以明显地提升混合像元分解的效果。 本文选取了机载可见光红外光成像光谱仪获取的赤铜矿地区作为真实的高光谱图像来测试新提出算法的有效性。该高光谱图像拥有224个波段,尺寸大小为250×191像素,移除那些被水蒸气吸收的波段,仅留下其中的188个波段进行实验。根据虚拟维度(virtual dimension,VD)算法[16]以及现有的对该图像地区的研究,端元的个数设为9,同时使用VCA和FCLS算法作为本实验中端元矩阵A和丰度矩阵S的初始化方法。 上述4种算法关于提取的端元之间的量化比较DSA值如表2所示。从表2中可以看出,在大部分情况下,NMF的解混结果比VCA要好。这是因为在该高光谱图像中是否存在纯像元是未知的,所以需要原图像中存在纯净像元的VCA算法效果最差,而NMF算法不需要原图像中存在纯净像元,其解混结果比VCA算法要好。同时也可以看出,新提出的MVSCNMF算法解混结果较其他的单一约束的非负矩阵分解算法(MVCNMF,L1/2NMF)要好。这是因为MVCNMF忽略了丰度的平滑性,L1/2NMF则忽略了端元的几何信息。在NMF的目标函数中,同时加入体积约束和平滑性约束可以比单约束的NMF带来更好的解混效果。本文选取了水铵长石和白云母两种地物解混的丰度图与其他方法进行对比,如图2、图3所示。白云母主要分布在图2左下方三角形区域以及图中间偏下的半圆形区域内,而水铵长石主要分布在以图3各小图中心为圆心的椭圆形区域内。与真实分布结果相比,就白云母的分解结果来看,本文的方法较其他方法有效地分解出了左下方三角区域。就水铵长石而言,本文的方法较其他方法也能够很好地剔除图像四周的非水铵长石部分。 表2 真实高光谱图像实验中不同方法下DSA值比较 图2 各算法分解的白云母丰度图 图3 各算法分解的水铵长石丰度图 本文根据高光谱图像的端元和丰度的相关物理特性,提出了最小体积和平滑性约束的非负矩阵分解(MVSCNMF)算法。首先,利用端元的几何特性,将端元构成的单形体体积作为约束项添加到了目标函数中。其次,因为高光谱图像丰度分布具有平滑性,通过构造丰度的平滑性约束项,将其也添加到了目标函数中。最后通过优化求解算法,得到端元矩阵和丰度矩阵。合成的高光谱图像和真实的高光谱场景图像实验都表明,新提出的方法较原来的MVCNMF方法及其他流行的混合像元分解算法,解混效果都有了明显的提升,同时该方法不需要原始高光谱图像中存在纯净像元,适用于所有线性混合的高光谱图像。尽管本文可以提升混合像元分解的精度,但仍存在着矩阵分解迭代求解速度慢,且算法只适用于线性混合像元分解的场景等问题。为此,下一步将研究更为有效快速的矩阵求解算法,同时探索非线性混合模型的混合像元分解方法。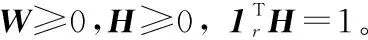
2 最小体积和平滑性约束的非负矩阵分解

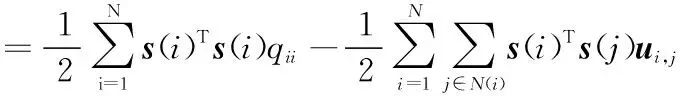
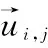
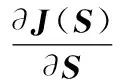
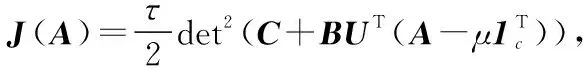
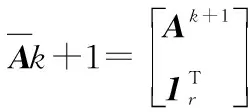

3 实验
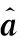
3.1 模拟实验数据
3.2 真实实验数据

4 结束语
