统计问题常见典型考题赏析

■姚践红

统计是高中数学的重要内容之一,也是新高考的必考知识点。高考主要考查随机抽样,考查用样本估计总体等。下面举例分析,供同学们学习与提高。

题型一:简单随机抽样

①从无数个个体中抽取50 个个体作为样本;②仓库中有1万支奥运火炬,从中一次性抽取100支火炬进行质量检查;③一彩民选号,从装有36 个大小、形状都相同的号签的盒子中无放回地抽出6个号签;④箱子里共有100个零件,从中选出10个零件进行质量检验,在抽样操作中,从中任意取出1个零件进行质量检验后,再把它放回箱子里。

解:根据简单随机抽样的特点逐个判断。①不是简单随机抽样,因为简单随机抽样要求被抽取的样本总体的个数是有限的。②不是简单随机抽样,虽然“一次性抽取”和“逐个抽取”不影响个体被抽到的可能性,但简单随机抽样要求的是“逐个抽取”。③是简单随机抽样,因为总体中的个体数是有限的,并且是从总体中逐个进行抽取的,是不放回、等可能的抽样。④不是简单随机抽样,因为它是有放回抽样。答案为③。

题型二:分层随机抽样

使用分层随机抽样的原则:将相似的个体归入一类,即为一层,要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则;为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,使每层样本数量与每层个体数量的比等于抽样比。

例2 某校500名学生中,O 型血有200人,A 型血有125人,B 型血有125人,AB 型血有50人,为了研究血型与色弱的关系,需从中抽取一个容量为20 的样本。按照比例分配的分层随机抽样方法抽取样本,各种血型的人分别抽多少?

故O 型血抽8人,A 型血抽5人,B型血抽5人,AB型血抽2人。

题型三:获取数据的途径

获取数据的途径一般有四种:调查,试验,观察和查询。在应用以上四种方式获取数据时,要清楚数据的类型,选择适当的获取方式。

例3 为了缓解城市的交通拥堵情况,某市准备出台限制私家车的政策,为此要进行民意调查。某个调查小组调查了一些拥有私家车的市民,你认为这样的调查结果能很好地反映该市市民的意愿吗?

解:一个城市的交通状况的好坏将直接影响着生活在这个城市里的每个人,关系到每个人的利益。为了调查这个问题,在抽样时应当关注到各种人群,既要抽到拥有私家车的市民,也要抽到没有私家车的市民。

如果只对拥有私家车的市民进行调查,结果一定是片面的,不能代表所有市民的意愿。因此,要对生活在该城市的所有市民进行随机地抽样调查,不要只关注到拥有私家车的市民。

题型四:频率分布直方图的应用

例4 为了迎接某市作为全国文明城市的复查,爱卫会随机抽取了60位路人进行问卷调查,调查项目是自己对该市各方面卫生情况的满意度(假设被问卷的路人回答是客观的),以分数表示问卷结果,并统计他们的问卷分数,把其中不低于50 分的分成五段:[50,60),[60,70),…,[90,100]后画出如图1所示的部分频率分布直方图,观察图形信息,回答下列问题。

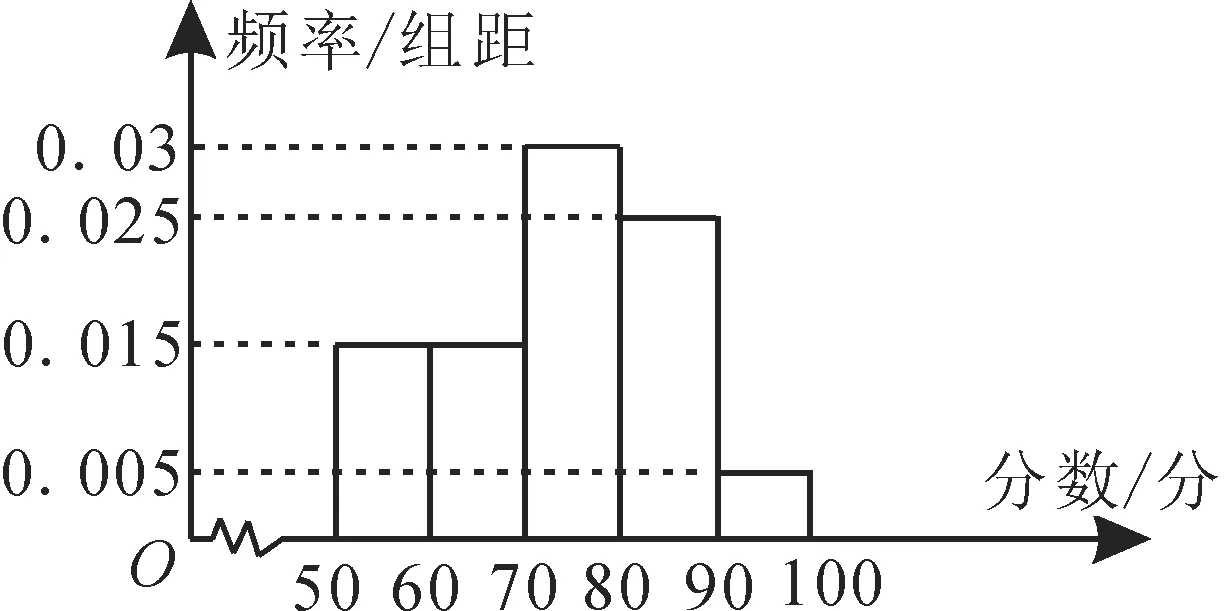
图1

(1)求出问卷调查分数低于50分的被问卷人数。

(2)估计全市市民满意度在60分及以上的百分比。

解:(1)因为各组的频率之和等于1,所以低于50分的频率为f=1-(0.015×2+0.03+0.025+0.005)×10=0.1,故低于50分的人数为60×0.1=6。

(2)依题意可知,60分及以上的频率和为(0.015+0.03+0.025+0.005)×10=0.75,所以抽样满意度在60分及以上的百分比为75%。

于是可以估计全市市民满意度在60 分及以上的百分比为75%。

题型五:百分位数的计算

一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值。计算一组n个数据的第p百分位数的三个步骤:第1步,按从小到大排列原始数据;第2步,计算i=n×p%;第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数。利用频率分布直方图求百分位数的方法:百分位数表示左侧小矩形的面积之和,先确定在哪个区间,再从左到右计算所有小矩形的面积和,百分位数所在区间需按照对应边比例计算面积。

例5 某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图2 所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.3,0.4,0.15,0.1,0.05。

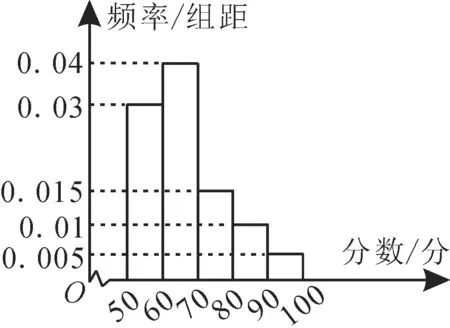
图2

求高一参赛学生成绩的第60百分位数。

题型六:众数、中位数、平均数的计算

众数、中位数及平均数都是描述一组数据集中趋势的量。平均数的大小与一组数据里每个数的大小均有关系,任何一个数据的变动都会引起平均数的变动。众数考查各数出现的频率,其大小与这组数据中部分数据有关,当一组数据中有不少数据重复出现时,其众数往往更能反映问题。中位数仅与数据的排列位置有关,某些数据的变动对中位数没有影响,中位数可能出现在所给数据中,也可能不在所给数据中,当一组数据中个别数据较大时,可用中位数描述这组数据的集中趋势。

例6 某公司的33名职工的月工资(以元为单位)如表1所示。

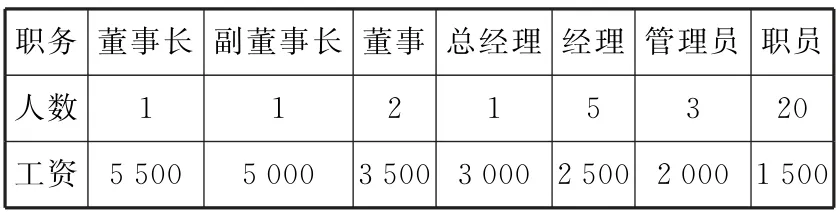
表1

(1)求该公司职工月工资的平均数、中位数、众数。

(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500 元提升到30000元,那么新的平均数、中位数、众数又是多少? (精确到元)

(3)你认为哪个统计量更能反映这个公司员工的工资水平? 结合此问题谈一谈你的看法。

(3)在这个问题中,中位数或众数均能反映该公司员工的工资水平。因为公司中少数人的工资与大多数人的工资差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平。

题型七:用样本的标准差、方差估计总体幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小。用样本估计总体时,样本的平均数、标准差只是总体平均数、标准差的近似。在实际应用中,常常把平均数与方差结合起来进行决策。在平均值相等的情况下,比较标准差以确定稳定性。

例7 从甲、乙两种玉米苗中各抽10株,分别测得它们的株高(单位:cm)如下。

甲:25,41,40,37,22,14,19,39,21,42。

乙:27,16,44,27,44,16,40,40,16,40。

(1)哪种玉米苗长得高?

(2)哪种玉米苗长得齐?

题型八:利用频率分布直方图求众数、中位数、平均数

频率分布直方图的数字特征:众数一般用频率分布表中频率最高的一组的组中值来显示,在样本数据的频率分布直方图中,众数是最高小矩形的底边中点的横坐标;在频率分布直方图中,中位数就是频率分布直方图面积的一半所对应的横坐标,中位数左边和右边的直方图的面积相等;平均数等于每个小矩形的高乘以底边中点的横坐标之和。

例8 从高三抽出50名学生参加数学竞赛,由成绩得到的频率分布直方图,如图3。

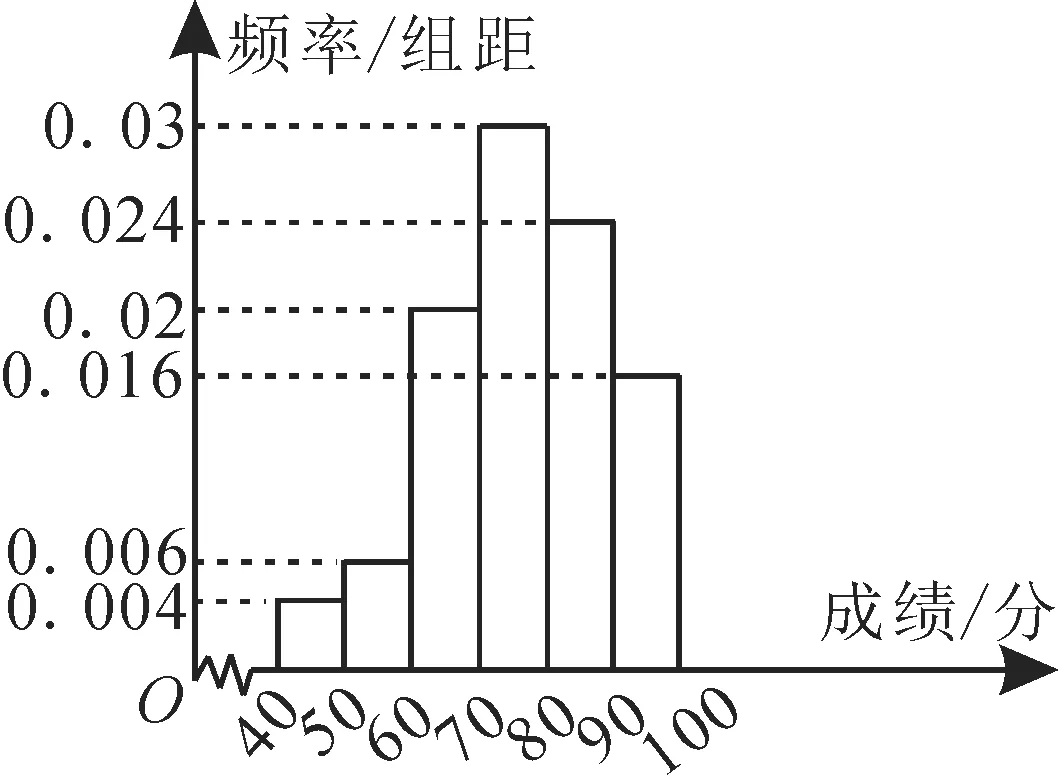
图3

由于一些数据丢失,试利用频率分布直方图求:

(1)这50名学生成绩的众数与中位数。

(2)这50名学生的平均成绩。

解:(1)由众数的概念可知,众数是出现次数最多的数。在频率分布直方图中,最高的小长方形的底边中点的横坐标即为众数,所以众数应为75。

由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等。因此在频率分布直方图中将所有小矩形的面积一分为二的垂直于横轴的直线与横轴交点的横坐标所对应的成绩即为所求。因为0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3,所以前三个小矩形面积的和为0.3。而第四个小矩形面积为0.03×10=0.3,0.3+0.3>0.5,所以中位数应位于第四个小矩形内。设其底边为x,则高为0.03。令0.03x=0.2,可得x≈6.7。故中位数约为70+6.7=76.7。

(2)样本平均值应是频率分布直方图的“重心”,即所有数据的平均值,也就是每个小矩形底边中点的横坐标乘以每个小矩形的面积之和。

所以平均成绩为45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85× (0.024×10)+95×(0.016×10)=76.2。

题型九:动态样本的平均数、方差问题

利用动态样本求平均数、方差的策略:平均数、方差的基本公式不变,但要注意变化前后的关系;适当结合平均数、方差的意义进行估值。

题型十:其他统计图表中反映的集中趋势与离散程度

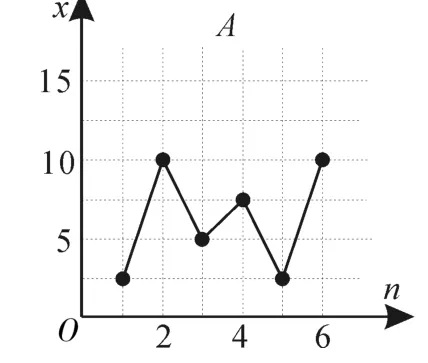
图4

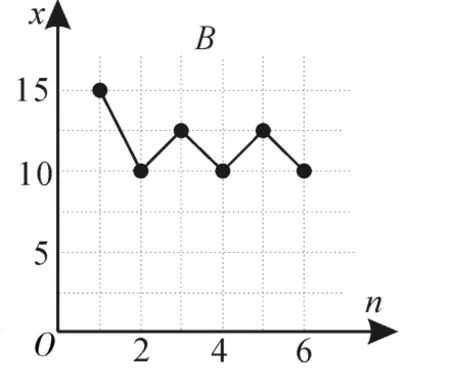
图5