执行器攻击下饱和受限异构多智能体系统滞后一致性控制
2022-05-18翁腾飞陈国荣袁艺云
韩 琦 张 澳 翁腾飞 陈国荣 王 慧 袁艺云
(1.重庆科技学院 智能技术与工程学院,重庆 401331;2.重庆科技学院 电气工程学院,重庆 401331;3.重庆师范大学 数学科学学院,重庆 401331;4.重庆市荣昌区职业教育中心,重庆 401331)
0 前 言
近年来,多智能体系统(Multi-Agent System, MAS)的分布式协同控制在各个领域得到了广泛应用,如智能电网协同控制、编队控制、振荡器同步等[1-2]。现有的大多数分布式一致性问题都是在假设执行器与传感器不遭受任何干扰的情况下进行的[3-5],但是MAS涉及智能体之间的通信和协作,极易遭受网络攻击。错误的执行器输入可能会严重破坏系统的稳定性,从而导致系统无法实现既定目标。
目前大部分的MAS安全一致性研究都是在同构系统上进行,在实际应用中,信息传递会受到各种限制,不同智能体需要实现不同目标,各个智能体的动力行为可能是不同的[6-9]。例如,图1所示的异构多车系统中,小车将接收到与其类别不同的信息,一些小车需要用非线性方程来建模,而另一些则需要用拉格朗日方程来建模。

图1 异构多车系统
针对智能体之间常常存在通信时延的问题,学者们开始对MAS的滞后一致性进行研究[10-11]。Wang等人研究了一阶MAS的滞后一致性问题,设计了基于局部信息的控制协议[12]。Li等人针对一阶和二阶智能体组成的MAS提出了新的滞后控制策略[13]。Fu等人设计的控制器解决了具有输入饱和的二阶MAS的控制问题[14]。在实际系统中,执行器元件受自身条件的约束,输出值往往有界,执行器通常受饱和约束[15]。目前大部分研究未考虑在执行器遭受攻击下,饱和受限异构MAS的滞后一致性问题。
1 基本定义及问题描述
1.1 基本定义
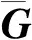

1.2 问题描述
根据跟随者在动力学的差异性,将其分为一阶智能体、一阶带有输入饱和约束智能体和二阶非线性智能体。
领导者的动力学方程表示为:
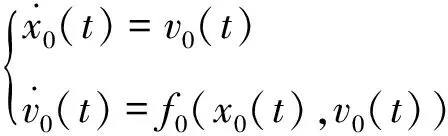
(1)

一阶智能体的动力学方程表示为:
(2)
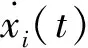
一阶带有输入饱和约束智能体的动力学方程表示为:
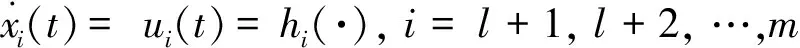
(3)
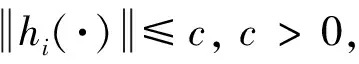
二阶非线性智能体的动力学方程表示为:
i=m+1,m+2,…,n
(4)
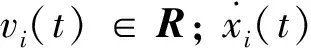
每个智能体i的执行器都有可能被损坏,对执行器的攻击可以描述为:
(5)
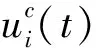

图2 多智能体系统在执行器遭受攻击时的架构图
定义1[12]对于常数τ>0及任意初始状态,式(1)—(4)的解满足以下条件:
多智能体系统的领导者与跟随者实现了滞后一致。在多智能体系统中,即使只有其中一个智能体执行器遭受攻击,也可能通过其节点邻居的通信放大,从而严重影响系统的稳定性。此时,n个异构跟随者的一阶和二阶智能体动力学方程可表示为:
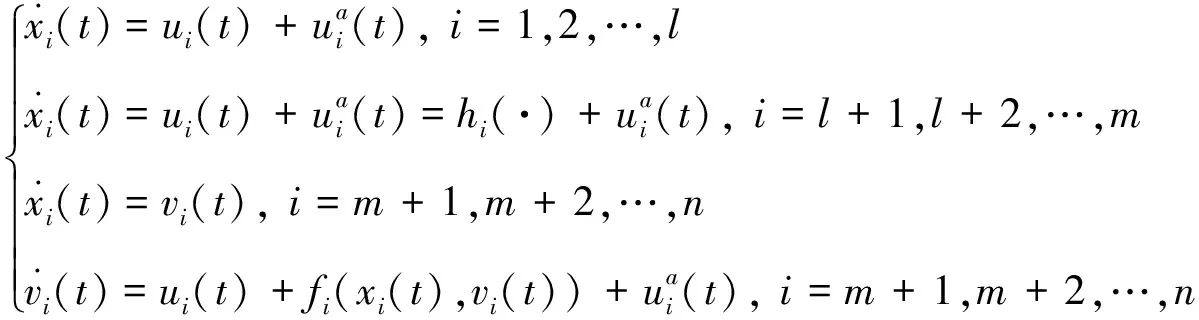
(6)
式中:i为1,2,…,l时,表示一阶智能体;i为l+1,l+2,…,m时,表示一阶带有输入饱和约束智能体;i为m+1,m+2,…,n时,表示二阶非线性智能体。
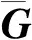
假设2存在非负常数ω,使得f0,fi满足:
|fi(xi(t),vi(t))-f0(x0(t),v0(t))|≤
ω|vi(t)-v0(t)|
为了方便理论分析,在此只考虑了一维Lipschitz条件,对于高维的情况可以采用克罗内克积进行推广。
2 结果分析
为了使领导者和n个追随者组成的异构多智能体系统达到滞后一致性,分布式控制算法设计为:
(7)
式中:k1、k2、k3表示控制增益,其值均大于0;aij表示智能体之间的连接关系,当智能体i与j相连时,aij>0,当智能体i与j没有相连关系或者i=j时,aij=0。
定理1在假设1、2成立的情况下,对任意的初始状态φ∈C([-τ,0];R)且满足ω-k3<0时,带1个领导者的异构多智能体系统(式(1)—(6)),利用设计的分布式控制算法可以实现领导-跟随滞后一致。

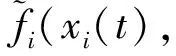
f0(x0(t-τ),v0(t-τ)),i=m+1,m+2,…,n
结合式(7),可以得到误差系统:
(8)
选择以下Lyapunov函数:
(9)
式(9)等式两边分别对时间求导,可得:

由于图G是无向的,因此可得到:
(11)
将式(11)代入式(10)可得:
若假设2成立,可得到:
(13)
结合等式(12)和不等式(13),可以得到:
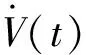

(14)
根据Lyapunov稳定性定理,可得到:
因此,饱和受限异构多智能体系统在执行器遭受攻击时,能实现领导-跟随滞后一致。
当τ=0时,所设计的控制算法可以解决执行器遭受攻击下饱和受限异构多智能体系统的领导-跟随一致性问题。采用牵引力控制的思想设计分布式控制算法,在拓扑图中,智能体i直接与领导者相连时,局部反馈控制增益bi>0。
3 算法流程图
分布式控制算法使领导者与追随者实现滞后一致,其算法流程图如图3所示。
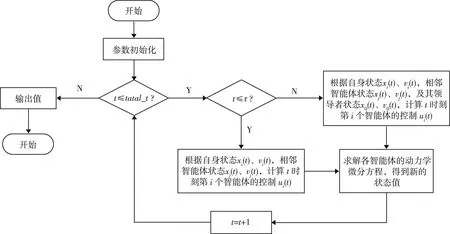
图3 分布式控制算法流程图
4 数值仿真验证


图4 异构多智能体系统拓扑图
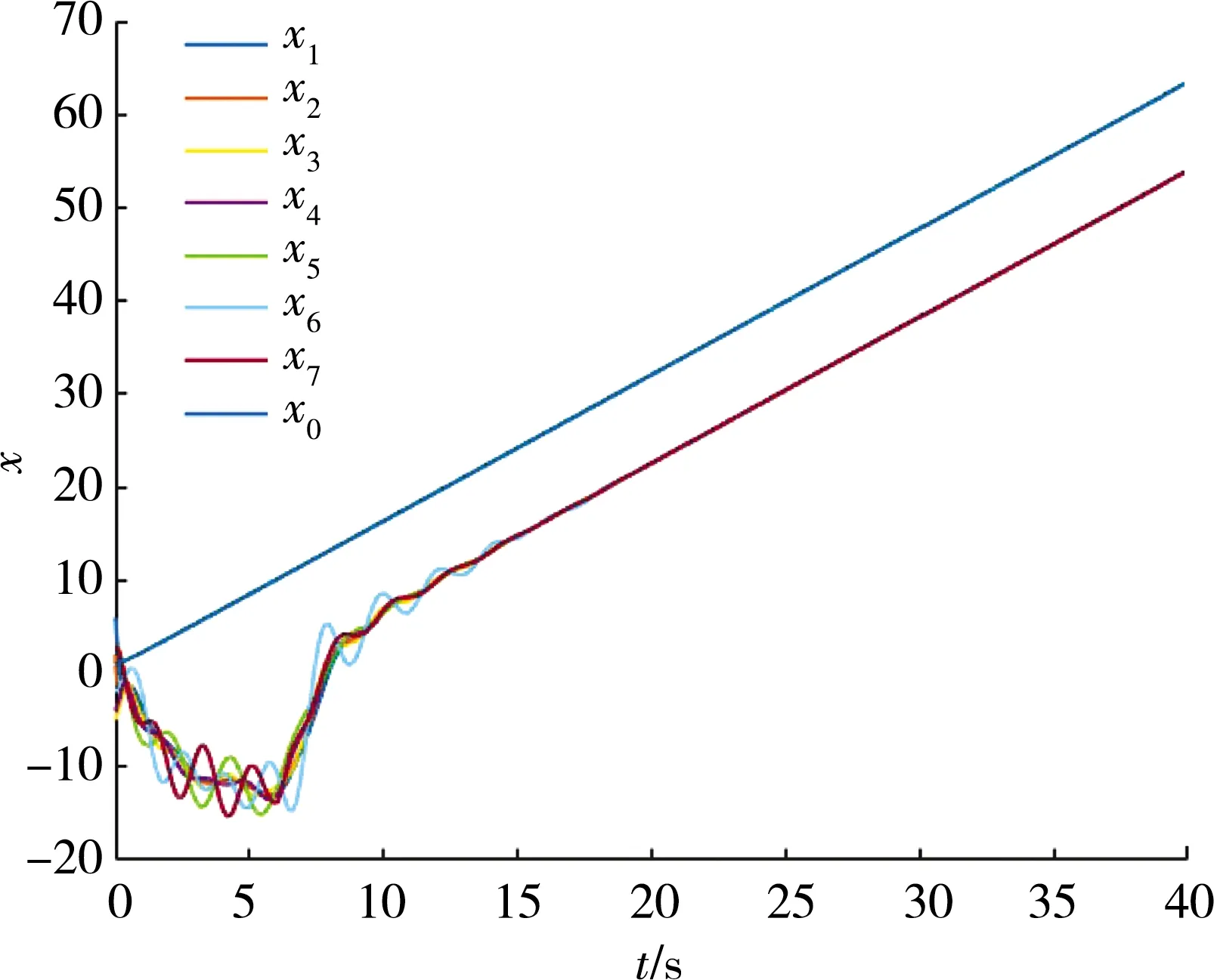
图5 跟随者滞后跟踪领导者的位置轨迹
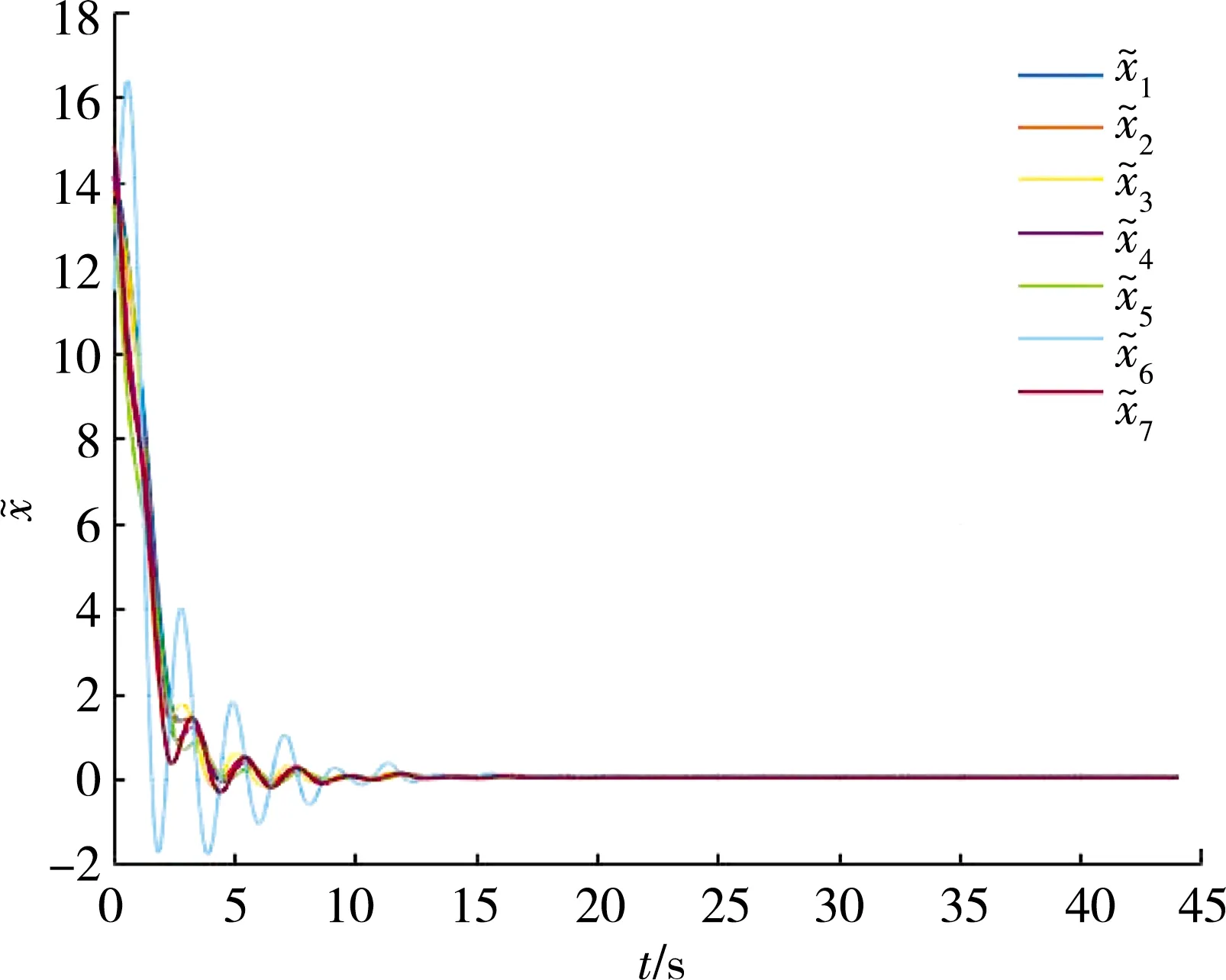
图6 多智能体系统滞后位置误差曲线
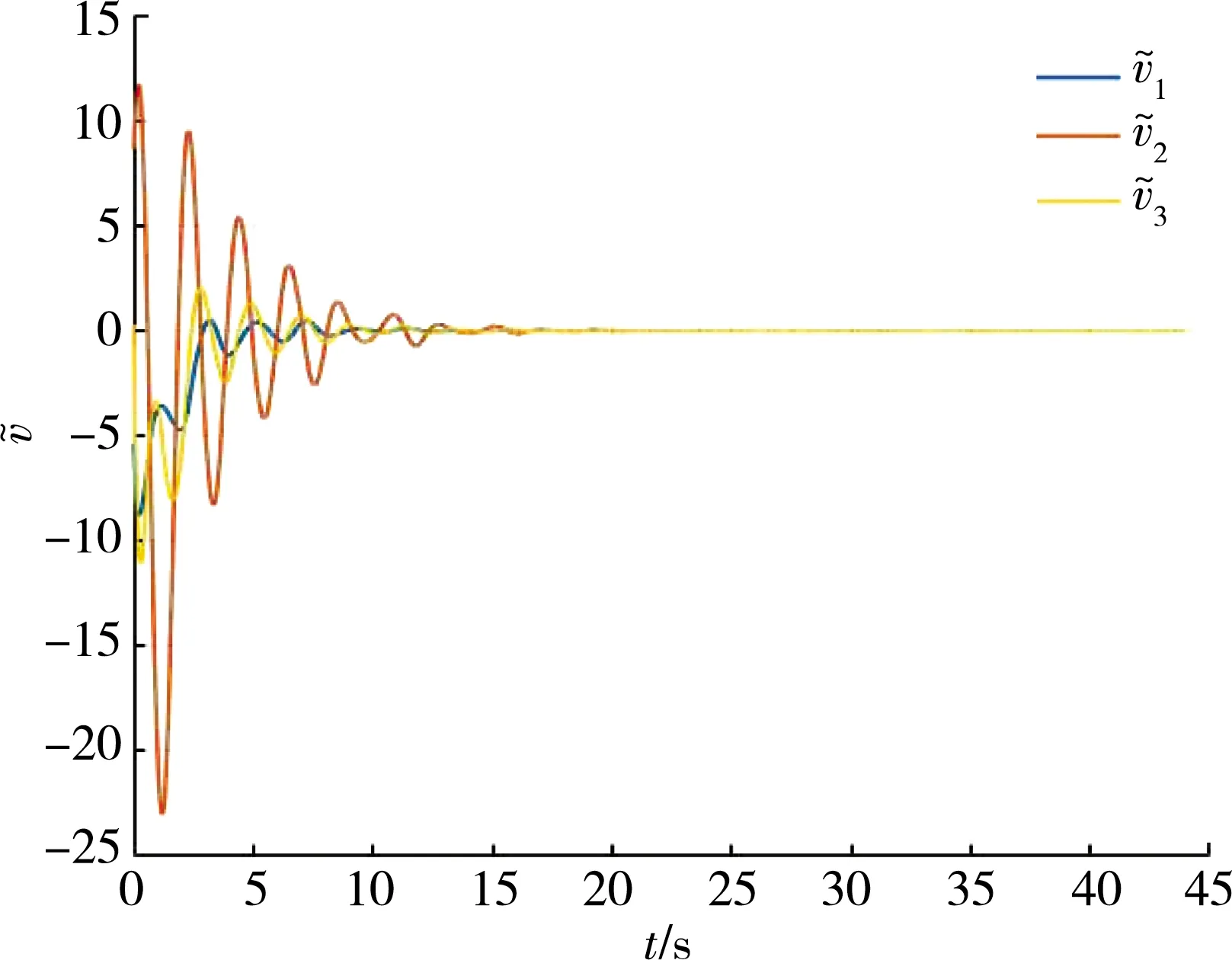
图7 饱和受限异构多智能体系统滞后速度误差曲线
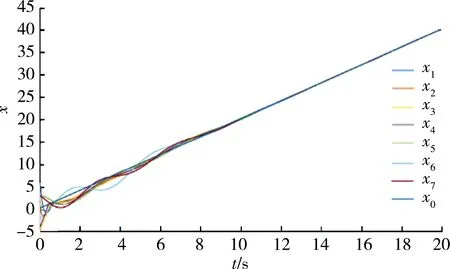
图8 领导者与跟随者位置轨迹
5 结 语
针对饱和受限的异构多智能体系统,考虑执行器遭受攻击的情况下,领导者与追随者的滞后一致性问题。提出了一种基于牵引控制的控制协议,应用Lyapunov稳定性理论分析系统的稳定性。通过数值仿真证明了控制协议的有效性,该算法能够有效抵御执行器攻击,使领导者和追随者在位置与速度上实现滞后一致。
