漂浮基空间机器人关节轨迹跟踪的时延估计控制

徐河振，于潇雁，2，陈 力

(1.福州大学 机械工程及自动化学院，福州 350116;2.流体动力与电液智能控制福建省高校重点实验室，福州 350116)

0 引言

随着空间技术的快速发展，太空的资源逐渐被重视起来，航天器在轨服务任务也逐渐增多，这些技术的革新给生活的通讯、遥感、数据传输等带来了巨大的便利。空间机器人技术也将在恶劣的外太空环境中完成大量的舱外任务，因此，空间机器人控制工程的研究成为热门话题之一［1-4］。其中存在大量影响空间机器人系统可靠性的因素，不仅包括诸多外部因素，如稀缺宝贵的燃料，外部环境的强干扰性，还包括内部因素，如非线性、强耦合性、奇异性、参数不确定性等，这些因素都将增加机器人系统控制器设计的难度［5-8］。因而针对非线性、强耦合性等问题，先进的控制方法，如自适应控制、模糊控制、滑模变结构控制等，在机器人系统中得到了广泛应用。

不同的控制方法各有优缺点，如滑模变结构控制法可控对象多样化，控制目标和应用范围广，控制策略针对不连续性问题有较好的应对方法，是非线性的控制方法，强大的鲁棒性和简单的结构备受机器人领域研究者的关注［9-11］。为了使机器人系统能够快速响应、较高精度地跟踪既定轨迹，基于时延估计的控制设计越来越受到研究者的关注，时延估计不需要知道被控对象的全部信息，易于设计和应用，还削去了控制参数的繁琐工作［12-14］。但是时延估计带来的误差及位姿状态带来非线性项，均会对系统的鲁棒性造成影响，需要结合先进的控制方法消除诸多因素的影响。

Jong 等［15］采用滑模控制方法提高时延的鲁棒性，但是传统滑模带来的抖振问题，会降低控制的品性。Jin 等［16］为获得机器人高精度的跟踪控制方法，引入非奇异终端滑模控制并结合时延估计策略，在无需获得机器人动力学模型全部知识的情况下，获得了较高的跟踪精度，但是控制精度有待提高。Dong 等［17］研究了存在非线性外部干扰时，对实时延控制的影响，然后提出基于梯度估计的时延控制策略。Zhang 等［18］研究了基于时延估计的一种鲁棒H∞有限时间跟踪控制器，采用高增益观测器对关节速度进行估计，具有较好的收敛性，闭环系统的证明显示较高的准确性和较强的鲁棒性可消除错误和外部干扰。Kali 等［19］针对没有驱动关节的仿人双足机器人，提出基于仿人双足机器人系统动力学鲁棒非线性控制器，基本思路是用时延估计方法逼近复杂动力学参数及干扰因素，然后导出滑模控制器，设计方案简单，但是动力学模型建立较为复杂，最后计算出的扭矩输入被转换为位置控制器，用于使用控制开关的伺服驱动，精度较高，收敛快速。Xu 等［20］研究了多智能体系统在有限时间内的一致性，并根据实时数据输出滑模控制参数。采取移动有限差分的方法对滑模面中的未知输出进行近似求解，对误差进行估计和细化，得到新的时滞关联滑动曲面，对其中存在估计偏差、奇异摄动和外部干扰等进行削弱。此方法可以在有限时间内减小误差，输入和输出的滑模控制具有简单的静态形式且没有引入额外的动态结构参数。Cmn 等［21］研究了线性时延系统下的滑模观测器状态及故障估计问题，对于观测状态和输出都有恒定的延迟。通过适当的系统变换滤波方法，提出了一种新的滑模观测器方案，解决状态的渐近稳定性和故障估计误差。

以上学者在时延估计方面做出了大量的研究，但是对于现有的时延估计控制，大部分的文献是针对参数不确定问题的研究，忽略了时延估计控制策略的响应灵敏性、时延估计时间较长、时延估计误差补偿控制的抖振等问题。本文主要以时延估计为主框架，对不确定参数进行在线估计，引入滑模变结构控制策略，滑模变结构控制策略具有响应快、对参数变化不灵敏、优化仿真的特点，但是滑模变结构控制在滑模面上因开关特性给系统带来了抖振问题，减小时延控制系统的跟踪幅度，使状态轨迹作小幅度、高频率的上下运动。通过在滑模变结构控制策略中创新性地引入趋近律的方法，确保到达滑动模态过程的动态品质，削弱高频控制信号的抖动，解决机械臂系统在操作过程中的抖振问题，最后通过三杆空间机械臂系统进行仿真验证。所设计的控制方法不仅能抵消不确定参数的影响，还能对时延估计误差做出补偿，大幅度提高控制系统的鲁棒性能，并且在时延估计过程中还能简化控制算法。

1 漂浮基空间机器人系统动力学模型的建立

首先是建立漂浮基空间机械人系统动力学模型，其几何结构如图1 所示，整个系统是由漂浮基座B0、刚性机械臂B1、刚性机械臂B2、刚性机械臂B3共同组成，且各组件Bi(i=0，1，2，3)之间均由刚性旋转铰链进行铰链接，然后建立平动惯性坐标系O-XY 与基座、机械臂的主轴联体坐标系(Oi-xiyi)，其中O0是基座B0的质心，Oi(i=0，1，2，3)为各关节铰中心位置，各机械臂杆Bi的质心Oci(i=0，1，2，3)在各转动杆的中心位置上。设O0O1之间的距离为L0，各机械臂Bi长度为Li(i=0，1，2，3)，Oi到Oci之间的距离为ai(i=0，1，2，3)。其中mi、Ji(i=0，1，2，3)分别为各分体的质量和中心转动惯量，C 为系统的总质心，M=m0+m1+m2+m3为系统的总质量。

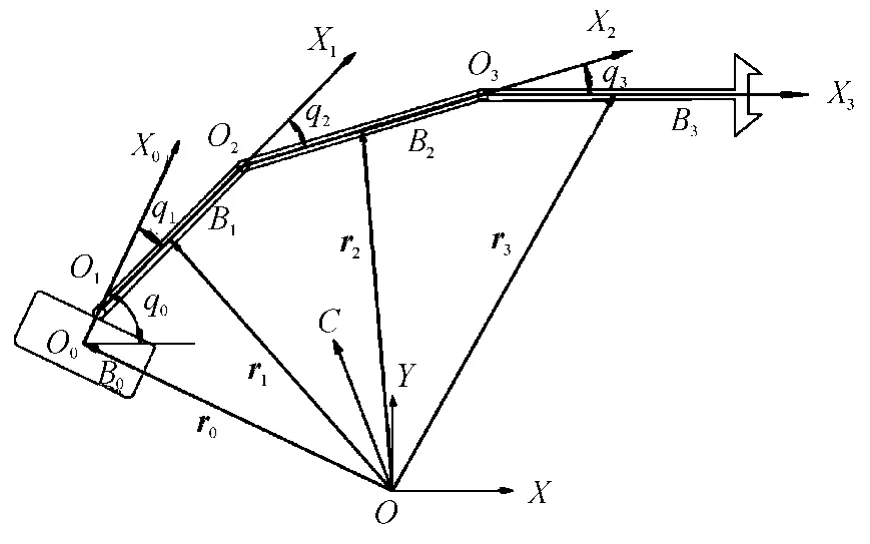
图1 漂浮基刚性空间机器人模型几何结构系统示意图

机器人系统在O-xy 平面内运动，各组件的几何位置关系可以表示出来，q0为基座B0的姿态角，q1、q2、q3分别为各机械臂关节角的相对转角，其中各组件的质心Oci对于原点O 的位置矢径为ri(i=1，2，3)，求ri对时间t 的导数便可得到各机械臂质心相对于惯性坐标系O-XY 的速度向量(i=1，2，3)。

在太空空间中，微弱的重力可以忽略不计，漂浮基刚性空间机器人在无外力作用下满足质心定理和动量矩守恒关系，即:

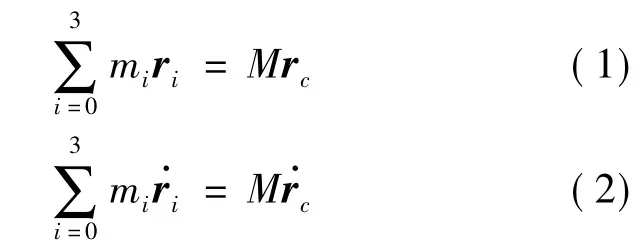
对于系统的动能T，有:

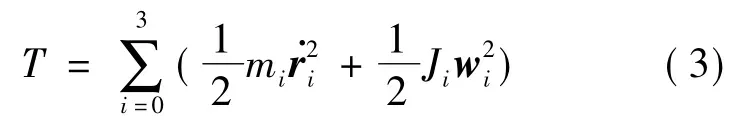
式中:wi为各组件i 的角速度向量;T 为一组适当选择的惯性参数的线性函数。忽略微重力作用，空间机器人系统的重力势能为零，可以联立Language 第二类动力学方程、动能定理、动量矩守恒等关系，得到位姿不受控的空间机器人系统的动力学方程:

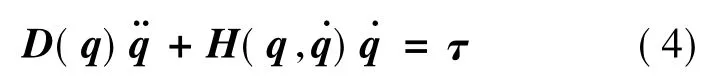
式中:q=［q0q1q2q3］T为系统载体姿态角和机械臂关节转角，D(q)∈R4×4的对称、正定系统惯量矩阵;∈R4×4是包含科氏力、离心力的正定矩阵，τ 为控制姿态角及3 个机械臂关节角的关节驱动电机输出力矩。

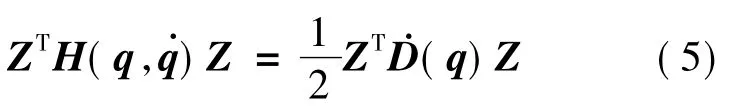
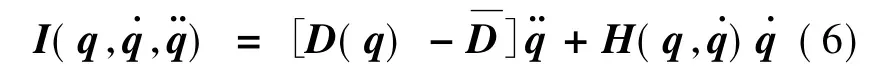
则对于漂浮基空间机器人动力学方程可写为:

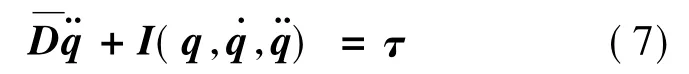
2 关于辅助参数的设计

对于漂浮基空间机器人系统结构复杂性以及动力学参数不确定性和非线性等问题，设计了轨迹跟踪控制方案，其目的是使其关节变量q 能够有效地跟踪上既定的期望轨迹qd，并且对于跟踪误差e 的要求，使其在有限时间内快速收敛到零。

设计理想状态下机械臂关节角的期望轨迹为qrd=［q1dq2dq3d］T，机械臂关节角的实际轨迹为:qr=［q1q2q3］T，则机械臂关节角误差可表示:

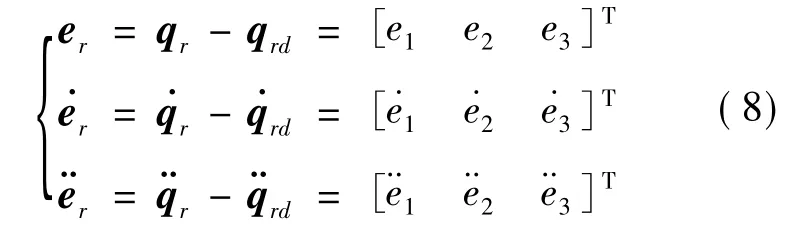
式中:ei=qi-qid，为机械臂各个关节角的误差(i=1，2，3)。

设计空间机器人系统的期望轨迹为qd=［q0］T，实际轨迹为。

同理，空间机器人系统各角度输出跟踪误差可以表示为:

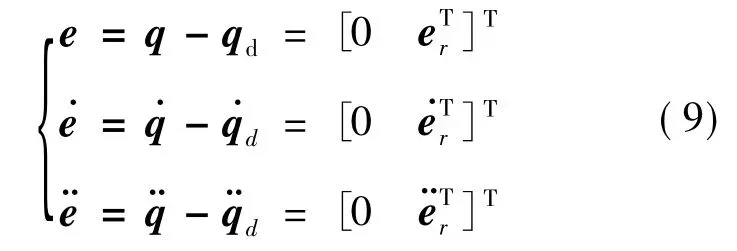
根据式(8)和式(9)引入系统辅助控制信号如下:

对式(10)求导得:

3 时延估计控制器的设计和分析

为了便于控制器的设计和分析，引入标准符号函数，定义如下:

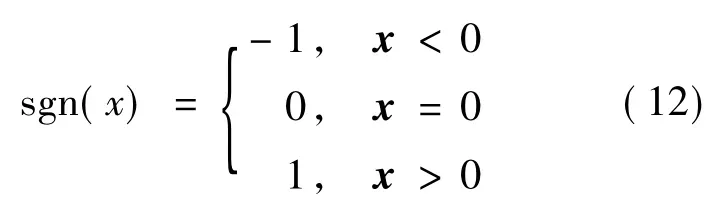
式中x=［x1x2… xn］T∈Rn×1。

3.1 控制器的设计

机器人控制律设计为:

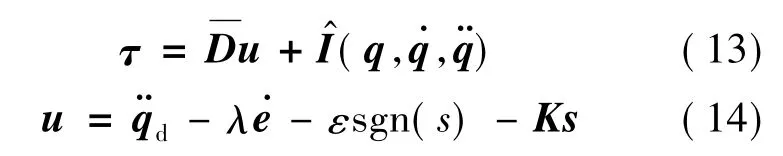
式中:ε＞0;K 为正常数对角矩阵。

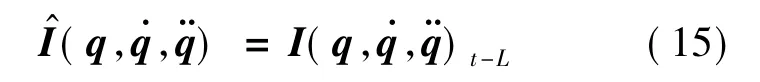
引入时延估计，定义*t-L为* 的时间延迟估计，t定义为当前时刻，L 定义为估计延迟时间，设计最小估计时间L 为采样周期，实际应用中，设置的采样频率大于30 倍系统宽带时，此时数字控制的系统可以看作是连续系统，对于选取的L 满足要求即可。

运用t-L 时刻采样点估算时刻的输出力矩，对于式(7)采用L 的估计时延可得:

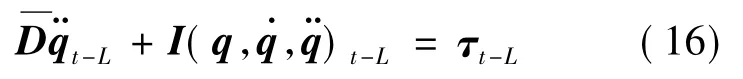
联立式(13)—(16)，则机器人控制律设计可以进一步改写为:

在机器人控制律设计中，如式(17)中，避免了复杂机器人动力学参数的获取，简化了仿真算法，但是在获取过程中会有所要求，可以利用对过去时间的控制输入和已知的过去角度进行在线获得，即t-L 时刻的关节加速度为:

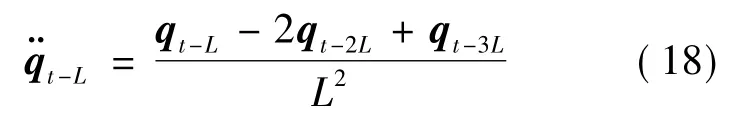
联立式(7)(13)可得:

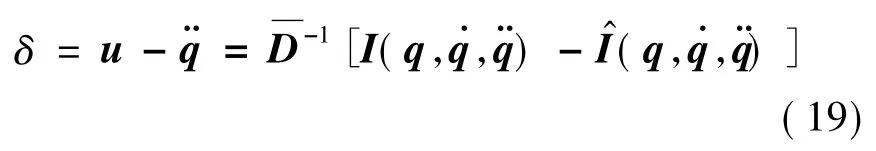
式(14)代入式(19)可得:

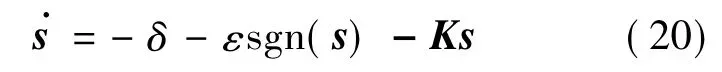
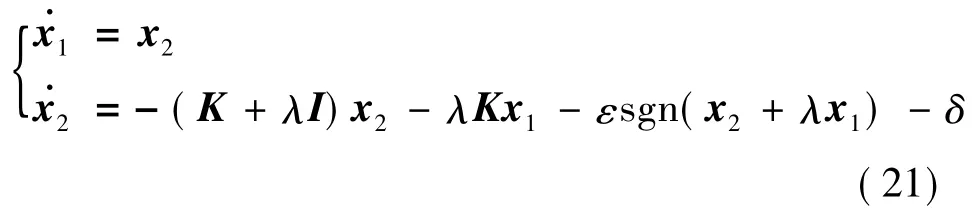
3.2 稳定性分析

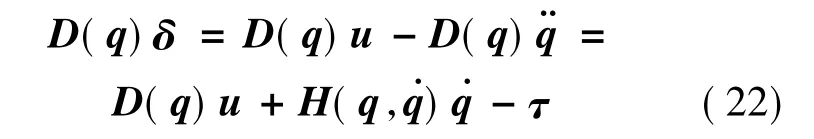
联立式(13)(15)(22)得:

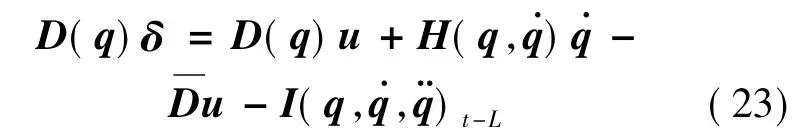
由式(6)可得:

式(24)代入式(23)可得:

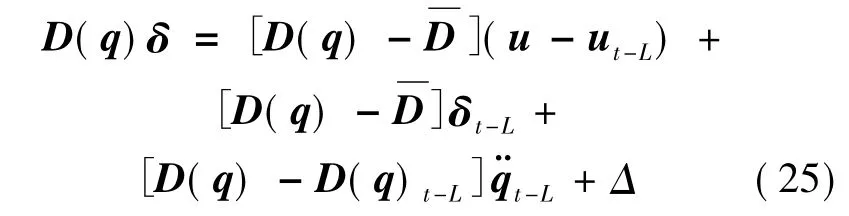
式中:

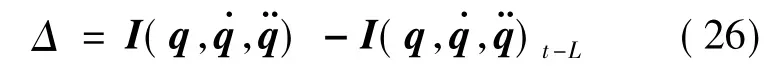
整理式(25)可得:

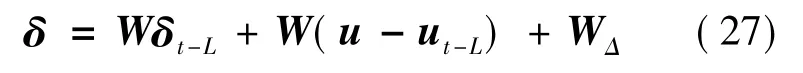
式中:

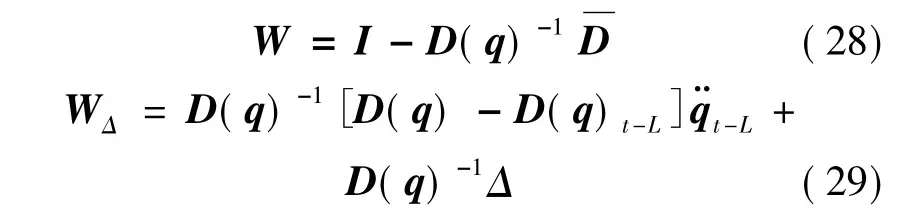
然后求V 关于时间t 的导数，可以得到:

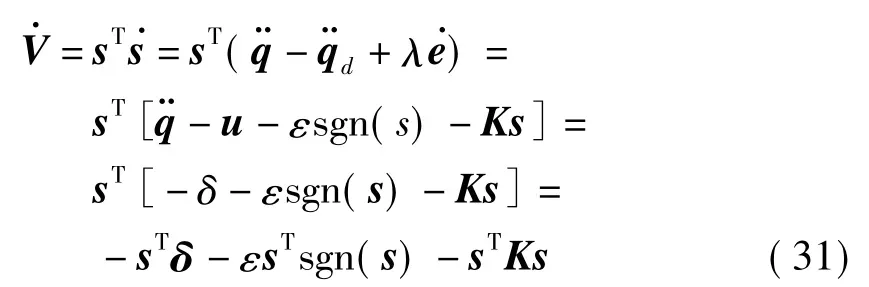
设计δ=［δ1，δ2，…，δn］T，s=［s1，s2，…，sn］T，K=diag(k1，k2，…，kn)且ki＞0，则式(31)可以改写为:

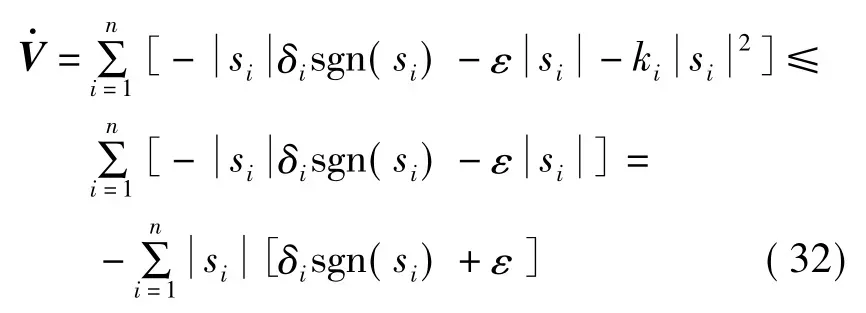
取足够小的时延时间L，在有限的时间内的某一时刻T，即存在t→T 时，s→0、，关于姿态角及关节角的跟踪误差e→0、。在式(21)中，可以认为时延估计δ 满足趋近于零的条件，可以将δ 看作是时延估计的误差的有界干扰项，即选择适当的、ε，可以保证系统的渐近稳定。

4 模拟仿真验证

为验证控制方法的有效性，本文采用数值仿真实验，所采用的漂浮基空间机器人模型见图1，该系统的参数设置如下:

m0=40 kg，m1=2 kg，m2=3 kg，m3=3 kg;J0=37.4 kg·m2，J1=1.5 kg·m2，J2=2.5 kg·m2，J3=2.5 kg·m2;L0=1.5 m，L1=3 m，L2=3 m，L3=3 m;a1=1.5 m，a2=1.5 m，a3=1.5 m。

设定漂浮基空间机器人载体姿态角和3 个关节角的期望轨迹如下:

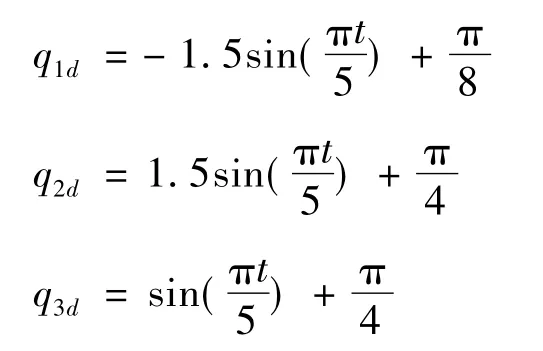
设置关节角的初始条件如下:q (0)=［0.5 0.5 0.7 0.9］T，采样周期=0.001 s，整个仿真过程耗10 s，控制参数如下:

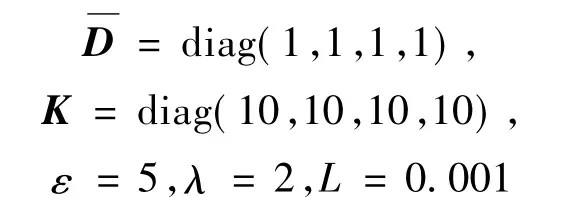
机械臂系统的控制仿真结果如图2—7 所示，图2—4 分别为机械臂关节角q1、q2、q3期望轨迹和实际轨迹曲线;图5—7 分别为机械臂关节角q1、q2、q3跟踪误差曲线。

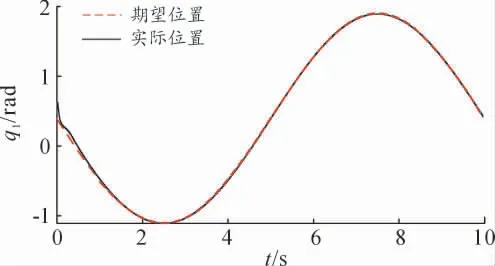
图2 关节角1 期望轨迹和实际轨迹的对比曲线

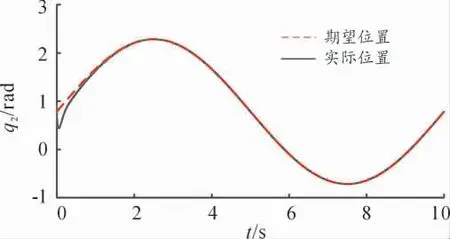
图3 关节角2 期望轨迹和实际轨迹的对比曲线

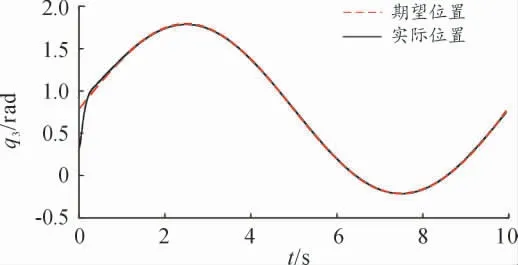
图4 关节角3 期望轨迹和实际轨迹的对比曲线

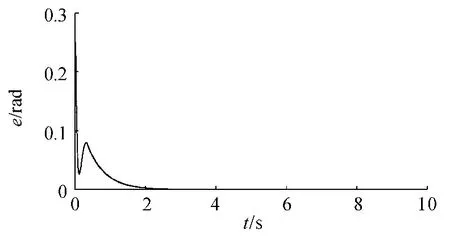
图5 关节角1 的跟踪误差曲线

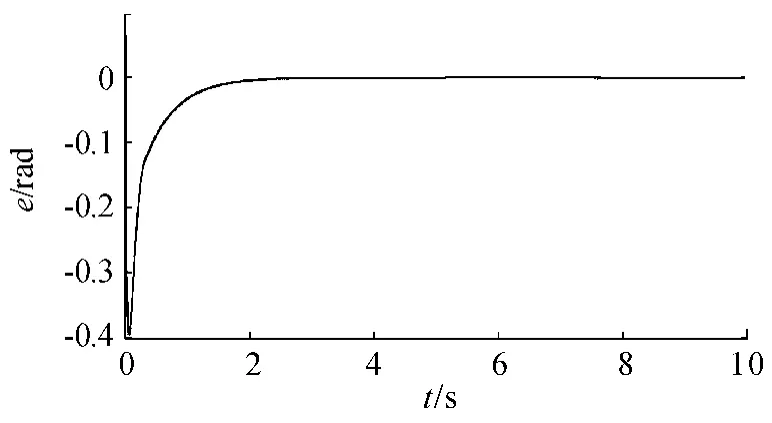
图6 关节角2 的跟踪误差曲线

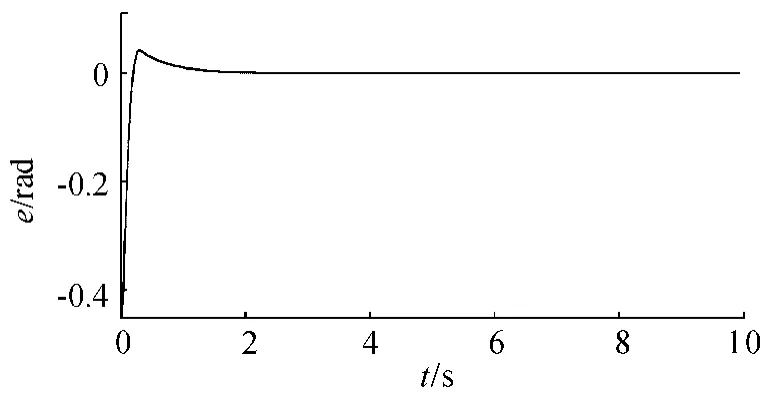
图7 关节角3 的跟踪误差曲线

从图2—4 可以看出，在有较大初始误差的情况下，通过所设计的时延估计控制策略能使机械臂各关节快速且平稳地跟踪上期望轨迹。在仿真的初始阶段，实际轨迹与期望轨迹之间存在一定的误差，这是仿真初始阶段所选取的初始值不在期望值上所引起的，然后由时延估计和滑模变结构控制对误差进行在线补偿，在滑动模态趋近滑模面时，添加趋近率控制，能有效减弱滑模控制带来的抖振问题，增加控制的动态品质。当时间到达2 s 时，各关节角的对比图显示实际轨迹已逼近期望轨迹，实现了有限时间内的快速跟踪，验证控制策略具有较好的快速响应性和较高的跟踪精度。从图5—7 可以看出，各关节角的轨迹跟踪误差曲线示意图显示初始阶段有一定的振荡，通过所设计的控制律对初始阶段的误差进行抑制和削减。当时间到达2 s 时，各关节跟踪误差到达平衡位置，误差收敛到0，各关节角的实际轨迹跟踪上期望轨迹，验证了该设计方案的快速响应性能和鲁棒性能。

5 结论

1)本文主要针对漂浮基空间机器人系统的跟踪控制进行设计，利用拉格朗日方程并结合动量守恒原理建立空间机器人动力学模型，通过增广变量法扩展变量的输入和输出，避免了对载体姿态不确定性的控制。

2)运用了时延估计方法，不仅有较强的抗干扰能力，而且还能有效避免控制参数带来的不确定性、耦合性、非线性等问题，能够对控制系统设计中的误差进行较好的补偿。

3)引入滑模变结构控制能很好地平衡机械臂系统运动的品性，能够在一定程度补偿时间延迟带来的估计误差，通过滑模变结构控制与趋近律的结合，修正关节角运动带来的跟踪误差，削弱传统滑模控制过程中的抖振，且控制算法也较为简单。该控制方案给系统带来很好的鲁棒性能，响应速度快，精度高，具有良好的动态性能和稳定性能。