工作井基坑开挖及吊装全过程土体应力路径研究

历朋林，朱士齐，刘 燕，曹 颖

(1.中铁十四局集团大盾构工程有限公司，江苏 南京 211800；2.中铁十四局集团有限公司，山东 济南 250101；3.济南大学 a.土木建筑学院，b.山东省城市地下工程支护及风险监控工程技术研究中心，山东 济南 250022)

在基坑工程的施工过程中，开挖卸荷、架设支撑、坑顶吊装等作用导致基坑周围土层应力状态变化复杂。土的应力-应变关系不仅与当前应力状态有关，还依赖于过去和新近的应力历史以及应力路径等诸多因素，因此利用常规三轴加载试验获得的参数进行基坑设计和数值模拟必然会产生较大的误差。研究[1-3]表明，在基坑开挖的典型卸荷条件下，土体产生剪应力，使得主应力轴转动，并产生明显的塑性变形，造成土体强度下降，宏观上表现为土体力学响应整体“软化”，如果忽视该特点而采用传统塑性理论进行设计，风险性较大。这也是在实际基坑工程中，将开挖后周边土体的变形量估计偏低而引起周边环境问题的因素之一。

在深基坑开挖过程中，土体的应力路径问题目前已为人们所关注和重视[4-8]。曾国熙等[4]总结得出基坑被动区土体单元侧向荷载不变、竖向卸荷，而主动区土体单元竖向荷载不变、侧向卸荷的结论。刘国彬等[5]进一步研究软土基坑被动区的土体应力，认为被动区土体竖向卸荷时，侧向荷载变化较复杂，可能不变或变大或变小，而坑外主动区土体应力路径则与文献[4]中的相同。吴宏伟等[6]对基坑卸荷应力路径进行定性研究，发现被动区土体有效应力路径等于室内不排水伸长试验的应力路径，而主动区土体的应力路径不同于室内不排水压缩试验的应力路径，但是袁静等[7]认为，基坑开挖中主动区和被动区均处于卸荷状态。何世秀等[8]通过真三轴试验模拟基坑开挖坑周土体应力路径，结果表明，应力-应变曲线在中主应力影响下变陡，极限应变减小，土体能承受更大的破坏应力。应宏伟等[9]提出了考虑主应力轴旋转的三维应力路径，并指出有必要提出考虑主应力轴旋转的基坑开挖典型应力路径，用以指导工程实践。

本文中针对复杂应力路径的应力-应变关系，采用有限元分析软件ABAQUS对基坑分层开挖和吊装施工全过程进行模拟，获取不同位置处土体单元在不同工况时的应力路径，研究土体单元变化规律，得出吊车荷载影响范围。

1 工程背景

济南黄河隧道盾构始发工作井基坑宽度为36.6～52.4 m，长度为150 m，覆土厚度约为3 m，底板埋深为26.2～31 m，最大挖深为31.2 m，顺作法施工，属深基坑，地层由上至下分别为填土、黏质粉土、粉质黏土、砂质粉土、粉质黏土、黏土、粉质黏土、细砂、粉质黏土。工作井附近地下水为第四系松散覆盖层的孔隙潜水，埋深为1.10～2.80 m，含水层主要为人工填土、黏质粉土、粉质黏土、粉细砂等，主要受水库、沉砂池、黄河以及降雨补给，排泄方式为径流、蒸发及人工开采等。

基坑采用地连墙和内支撑，地连墙厚度为1.2 m，深度为50 m，共设5道支撑，其中，第1、4道采用混凝土支撑，第2、3、5道采取钢支撑。济南黄河隧道盾构始发工作井基坑的支护结构平面及尺寸如图1所示。

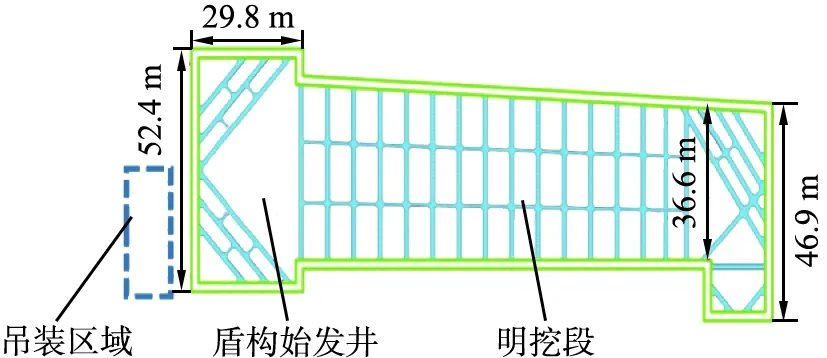
图1 济南黄河隧道盾构始发工作井基坑的支护结构平面及尺寸

2 考虑主应力轴旋转的应力路径描述

刘熙媛等[10]将基坑开挖阶段周围土体分为3个区域，在基坑开挖过程中，各区域土体的典型应力路径不相同，如图2[10]所示。

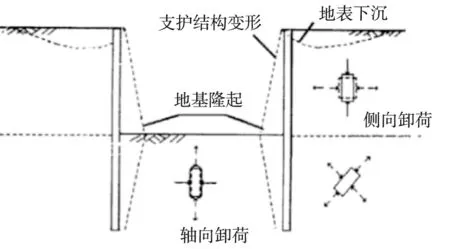
图2 基坑开挖影响区域划分[10]

采用p、q、α这3个参数描述二维平面中土体单元的应力状态变化，其中p为平均压应力，q为广义剪应力，α为大主应力旋转角，定义为大主应力与竖直方向夹角，顺时针旋转的α值为正[9-10]，如图3所示。

σ1—大主应力；σ3—小主应力；α—大主应力旋转角。图3 二维平面中土体单元的大主应力旋转角示意图

在二维分析中，通常可假定中主应力等于小主应力，假设土体单元中某点应力状态为σ={σx,σy,τxy}，则

(1)

(2)

(3)

式中：σx为x方向的主应力；σy为y方向的主应力；τxy为xoy平面的切应力。

3 有限元数值模拟

3.1 模型建立

有限元整体模型尺寸为80 m×100 m(宽度×长度)，围护结构采用地连墙和内撑，均采用一维梁单元模拟，地连墙深度为50 m，厚度为1.2 m，梁单元表面与土体单元表面采用带(Tie)接触，两侧限制模型水平位移，底部限制水平、竖向2个方向位移。土体采用修正剑桥模型，在吊装阶段采用QUY650型履带吊，吊装质量为370 t的盾构刀盘。履带吊自重为775 t(包含机身自重、车身配重、中心压重及超起平衡重)。基坑开挖阶段遵循分层开挖分层支撑的施工顺序，待底板施工完毕后开展吊装工作。济南黄河隧道盾构始发工作井基坑的施工模拟工况如表1所示。

表1 济南黄河隧道盾构始发工作井基坑的施工模拟工况

3.2 本构选取

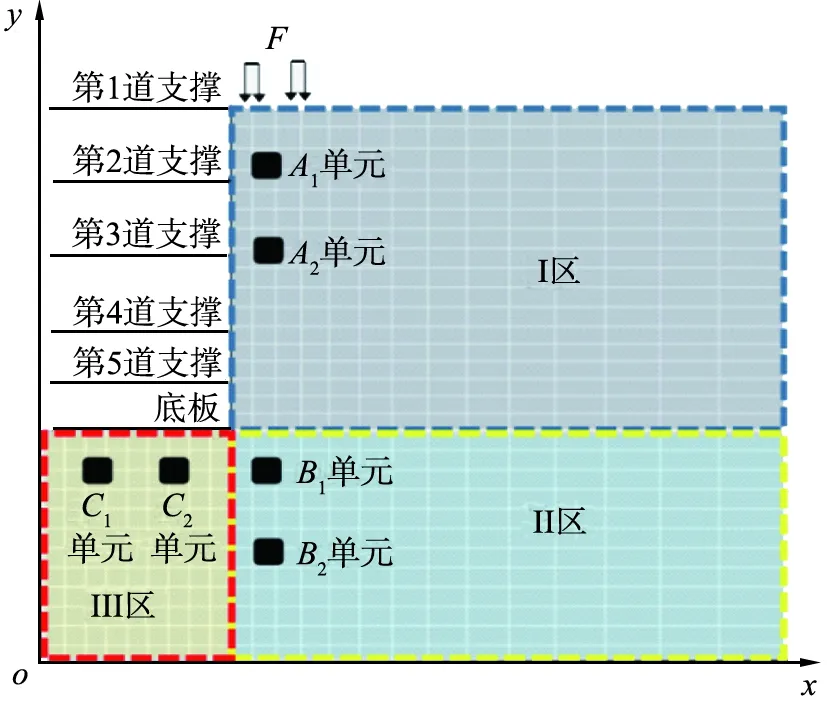
F—坑顶吊装荷载，包括履带吊荷载和盾构刀盘荷载；A1、A2、B1、B2、C1、C2—选取的6个典型土体单元，具体位置坐标分别为A1(16,100)、A2(16,90)、B1(16,72)、B2(16,52)、C1(5,72)、C2(10,72);xoy—平面直角坐标系。图4 济南黄河隧道盾构始发工作井基坑的施工模拟典型土体单元位置坐标及编号

4 考虑主应力轴旋转的应力路径分析

4.1 主动区

土体单元A1、A2位于支护墙体正后方的主动区位置，图5所示为济南黄河隧道盾构始发工作井基坑自基坑开挖到吊装刀盘完成时土体单元A1、A2

p—平均压应力；q—广义剪应力；α—大主应力旋转角；σy,0—基坑未开挖时土体单元的竖向应力。图5 济南黄河隧道盾构始发工作井基坑自基坑开挖到吊装刀盘完成时土体单元A1、A2的应力路径

(a)A1单元

4.2 被动区

p—平均压应力；q—广义剪应力；α—大主应力旋转角；σy,0—基坑未开挖时土体单元的竖向应力。图7 济南黄河隧道盾构始发工作井基坑自基坑开挖到吊装刀盘完成时土体单元C1、C2的应力路径

(a)C1单元

4.3 过渡区

p—平均压应力；q—广义剪应力；α—大主应力旋转角；σy,0—基坑未开挖时土体单元的竖向应力。图9 济南黄河隧道盾构始发工作井基坑自基坑开挖到吊装刀盘完成时土体单元B1、B2的应力路径

5 吊车荷载影响范围分析

由应力路径分析可知，当吊车荷载作用时，大主应力旋转角会逆时针旋转，产生回转现象，现取距吊车荷载水平距离分别为0、3、9、12、18、24 m的6个断面，以每个断面深度为纵坐标，吊车荷载作用前后大主应力旋转角差值为横坐标，绘制大主应力旋转角差值分析图，如图11所示。根据大主应力旋转角差值的大小，将荷载作用宽度为0～9 m、深度为0～12 m的范围定义为主要影响区，深度约为荷载作用宽度的1.3倍。宽度为9～18 m、深度为12～20 m的范围定义为次要影响区，宽度为18 m、深度为20 m之外的范围定义为无影响区，各影响区土体单元大主应力旋转角差值约为最终旋转角的0～1/4。具体吊装荷载影响范围如图12所示。

(a)B1单元

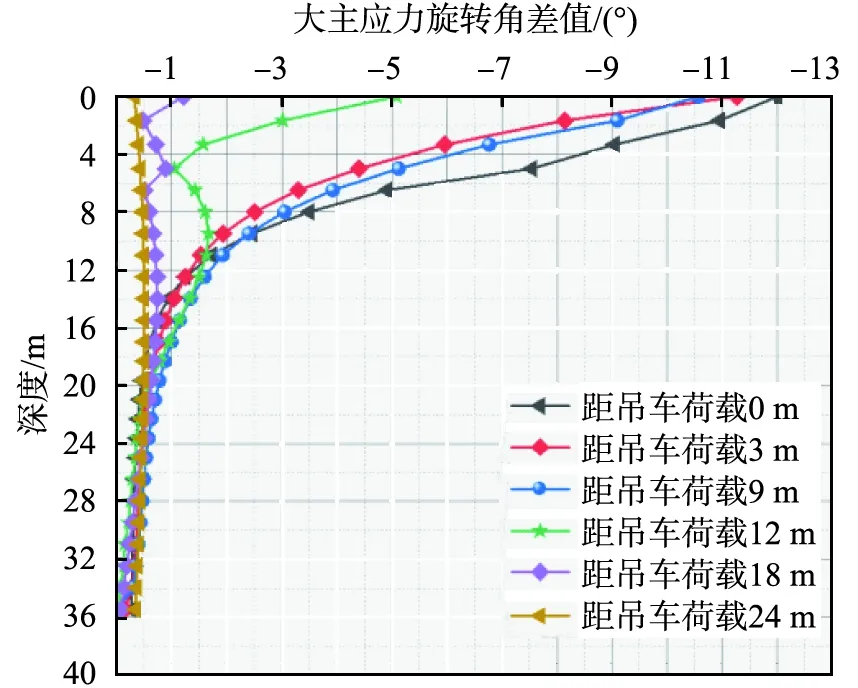
图11 济南黄河隧道盾构始发工作井基坑的吊装完盾构刀盘时6个断面的大主应力旋转角差值

6 结论

本文中以济南市黄河隧道盾构始发工作井为研究实例，运用有限元分析软件ABAQUS，根据现场实际施工过程，分析不同区域、不同施工工况时土体单元的大、小主应力及大主应力轴旋转情况，得出以下主要结论：

F—坑顶吊装荷载，包括履带吊荷载和盾构刀盘荷载。图12 吊车荷载影响范围示意图

1)与传统二维应力路径平均压应力—广义剪应力相比，考虑主应力轴旋转时，三维应力路径平均压应力—广义剪应力—大主应力旋转角更能具体反映不同土体单元不同工况时的应力路径状态。

2)在基坑开挖阶段，坑底土体单元主要为竖向卸荷，卸荷前竖向应力为大主应力，开挖后竖向平均压应力不断减小，广义剪应力不断增大，大主应力轴发生较大角度的旋转；而坑外土体单元以侧向卸荷为主，大主应力轴旋转较小。

3)坑内土体单元大主应力轴旋转明显，随着基坑的开挖，大主应力旋转角呈阶跃式增大，缺少中间过渡阶段，最终大主应力旋转角接近90°，并且旋转程度呈现空间性特征，随着与基坑中心距离的增大，大主应力旋转角逐渐减小，这与常规三轴加载实验的工况有很大区别，因此基坑开挖阶段土体参数应考虑坑内土体的应力旋转效应。由于坑外土体单元主应力旋转角度较小，因此在计算时可不考虑主应力轴旋转的影响。

4)在开挖到底后的吊装阶段，吊车正下方的土体单元的大主应力旋转角产生较大的逆时针旋转，约为最终旋转角的0～1/4，而吊装对坑内土体的影响较小。此外，吊装荷载的影响范围主要发生在吊车下方深1.3倍荷载宽度的三角形范围内，1.3～2.0倍深度范围为次影响区。