基于混合应力法的XLPE绝缘电压耐受指数评估研究

陈新岗，刘新宇，马志鹏，朱莹月，谭 悦，崔炜康，王梅林

（1.重庆理工大学，重庆 400054；2.重庆市能源互联网工程技术研究中心，重庆 400054）

0 引言

随着电网的发展，高压直流输电凭借其灵活性好、输电距离远等优点得到了广泛应用[1]。交联聚乙烯（XLPE）直流电缆作为柔性直流输电工程中的关键设备之一，其绝缘老化失效机理和寿命评估的研究一直都是高电压绝缘领域密切关注的问题。其中，老化寿命模型是固体绝缘材料研究的重要成果之一。反幂模型是典型的电寿命唯象模型，凭借其简洁的表达式和明确的参数含义而被广泛应用于电缆绝缘老化失效机理与寿命评估的研究[2]。

电压耐受指数n是反幂模型中的重要参数，在实际工程中得到广泛的应用。n的数值可以表征电力电缆在电应力作用下的长期耐受能力。在电缆绝缘设计中，可以根据n值确定电缆的老化系数，并设计出电缆绝缘层的厚度[3]。另外，电缆在其出厂前的多种检测试验的电场选取都要参考n值的大小[4]。国内外学者根据反幂模型对n的数值进行了大量的研究。文献[5]针对XLPE及其纳米复合材料在不同的温度下进行了加速电寿命试验。结果表明，计算得到的n值随着试验温度的升高而增大。文献[6]利用空间电荷积聚造成的宏观现象在现有反幂模型数学表达式中引入修正系数，得到的n值随着样品厚度的增加而增大。文献[7]采用极大似然法分析了加速电寿命试验数据并求得相应的n值，但该方法只通过变压器匝间油纸绝缘模型进行了验证。文献[8]利用Weibull分布统计分析结合最小二乘法计算出电缆的形状参数和尺度参数进而计算得出n值，但该方法只进行了模拟仿真，没有进行试验验证。

综上所述，寻找合适的方法来获取直流电缆电压的耐受指数进而评估电缆电寿命是目前研究与工程应用领域需要解决的问题。因为直流电缆在正常工作状态下的失效过程是缓慢的，所以加速寿命试验是解决上述问题的有效方法[9]，其中恒定应力法最为常用。文献[10]对直流电缆切片施加40 kV/mm的恒定直流电场，通过对样品空间电荷特性进行分析，表明其具有抑制空间电荷和耐电老化的能力。文献[11]自主搭建了恒定应力试验装置，通过试验获得了试样电缆的电压耐受指数n为14.03。然而，恒定应力法存在试验耗时长的缺陷，通常获取单一样品的电压耐受指数需花费数天乃至数十天时间，不利于其进一步的推广应用。

本研究提出一种混合应力试验方法，首先，根据反幂模型和累积损伤模型建立满足恒定应力试验和序进应力试验等效性的条件；其次，通过不同电压上升率的序进应力试验得出满足等效性条件的最佳电压上升率；最后，采用混合应力试验方法对XLPE薄片按照“序进-恒定-序进”应力顺序进行加速寿命试验，根据样品失效时间结合Weibull分布统计结果求得样品的电压耐受指数。

1 两种加速寿命试验方法的等效性建立

1.1 在恒定与序进应力试验中应用的反幂模型

恒定应力加速寿命试验通常是对样品施加高于其正常耐受水平的恒定电压来加速其老化，并记录每个样品从施加电压开始到被击穿时的时间与场强。将其放入lnE-lnt坐标系中绘点，最后将所有的点拟合成一条直线，如图1所示。该方法应用较广，但是存在耗时长、试验结果分散等缺点。

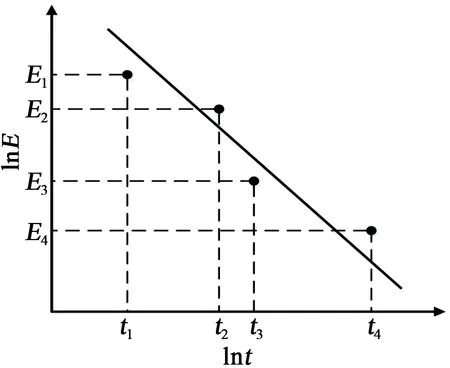
图1 恒定应力法时间与场强的关系Fig.1 The relationship between time and field strength of constant stress method

拟合的直线表达式满足式（1），该式也可由反幂模型等式两边取对数获得。

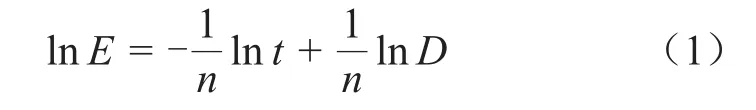
式（1）中：E为电场强度；t为电场强度E下绝缘材料被击穿的时间；D为材料失效所需的累计损伤量；n为电压耐受指数。

序进应力试验是指对样品施加时刻改变的应力，最常用的是施加随时间线性上升的电压，如图2所示。

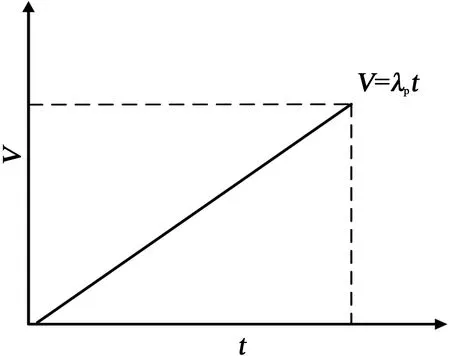
图2 序进应力法施加电压与时间的关系Fig.2 The relationship between applied voltage and time of sequential stress method

序进应力的理论基于W NELSON提出的反幂模型的累积损伤分析，其表达式如式（2）所示。

式（2）中：Vc为恒定应力的失效电压；tc为恒定应力的失效时间；n为电压耐受指数；Dc为电压Vc在tc时间内对样品造成的损伤量。

通过式（2）也可以将序进应力试验数据运用于绝缘材料的寿命分析中[12-16]。采用该方法对直流电缆进行寿命评估时，通常需要通过反幂模型建立序进应力试验与恒定应力试验方法的等效关系。

1.2 恒定应力与序进应力试验的等效性分析

要使序进应力试验与恒定应力试验等效，必须基于两个假设：①累积损伤量D达到阈值时,被测样品发生绝缘击穿，在此过程中累积损伤量可变；②任意时刻变化的累积损伤量都可使用式（2）所示的反幂模型来表示。

在序进应力试验中电压随时间发生变化，因此样品的累积损伤量也随加压时间而变化。这一过程中，产生的累积损伤量可采用积分的方法表示，如式（3）所示。

利用式（7），在恒定应力加速寿命试验和序进应力加速寿命试验采用相同的试样且已知n值的情况下，根据一种试验的失效时间就可预测另一种试验的失效时间，从而建立起恒定应力法与序进应力法的等效关系。这种等效关系为使用混合应力法进行电压耐受指数n的评估提供了理论依据。

1.3 混合应力试验评估电压耐受指数

恒定应力试验存在耗时长、样品之间的电压耐受能力存在差异、施加恒定电压的选值困难等缺点。使用混合应力试验进行电缆电寿命的评估能够有效避免上述缺点。

混合应力试验由恒定应力试验和序进应力试验混合构成，可分为3个阶段，如图3所示。第1个阶段是序进应力试验，对样品施加上升率为λp的变化电压，电压从0 kV上升到选定的电压，记录时间tp1；第2个阶段对样品进行选定电压下的恒定应力试验，记录时间tc；第3个阶段为序进应力试验，对样品施加上升率为λp的变化电压，电压从选定电压上升至样品发生击穿，记录击穿电压Vt和击穿时间tp2。运用序进应力试验与恒定应力试验的等效性：假设存在一个n值，可以将第1阶段与第3阶段序进应力试验总时间转化为等效的恒定应力试验时间。将该时间与第2阶段恒定应力试验时间相加即可得到混合应力试验的总时间。

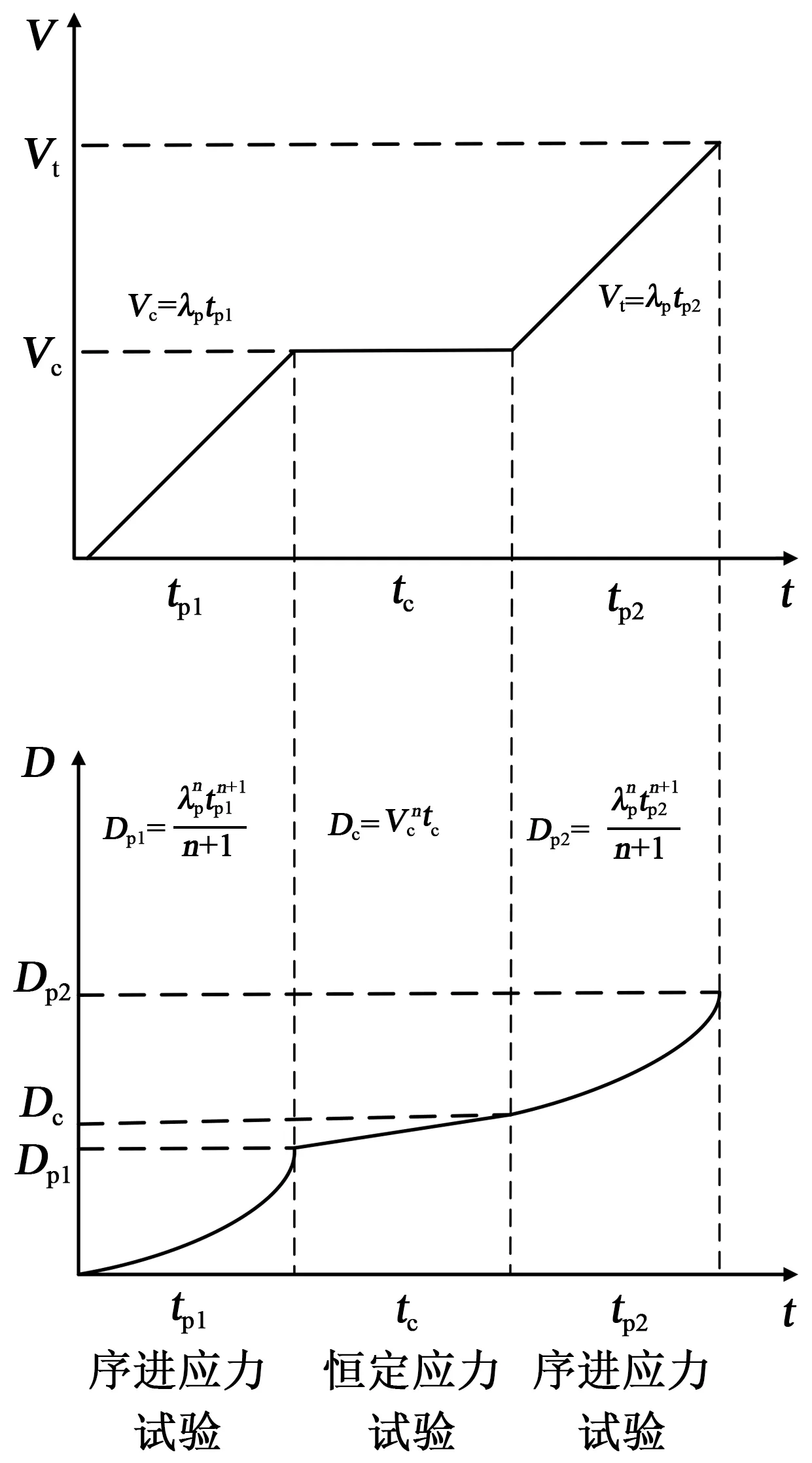
图3 混合应力法Fig.3 Mixed stress method

因为恒定应力试验和序进应力试验的击穿时间都符合Weibull分布，则等效的混合应力试验时间也符合Weibull分布。根据Weibull定律，样品的累积击穿概率F(ti)可表示为式（8）。

式（8）中：N为试验样品总数；i表示从试验开始到任意试验时间t后的样品累计击穿个数。

因此，可以进行不同选定电压Vc下的多组混合应力试验，得到每组试验的混合应力击穿时间。将该时间结合Weibull定律转化为尺度参数t，即为XLPE被测样品在Vc下的电寿命。把不同的尺度参数t和选定场强代入式（1）中并在双对数坐标系中绘制出一条直线，通过该直线可以求取电压耐受指数和累积损伤量。

混合应力试验中第1阶段和第3阶段的序进应力试验可以有效减少XLPE电缆老化的时间，防止长时间加压试验中外部环境变化造成的干扰。第2阶段的恒定应力试验可以使绝缘材料最终的失效形式为电热击穿，保证一定的安全裕度，预防短时击穿造成的试验误差，使最终算出的电压耐受指数更接近于真实值。

因此，混合应力法是评估被测XLPE样品电压耐受指数的有效方法。然而，混合应力法的合理应用需建立在试验参数如序进升压的升压速率λp的优化选取基础上。因此有必要继续研究最优试验参数的获取方法。

2 序进应力最优试验参数

2.1 最优试验参数的求取方法

选取一个合理的序进应力电压上升率λp范围，并在该范围内选取若干个 λp数值：λ1、λ2……λi。采用同批次 XLPE样品分别以 λ1、λ2……λi作为升压速率进行序进应力击穿试验。相邻λ之间可以求取一个该电压上升率范围下的假定电压耐受指数，如图4所示。

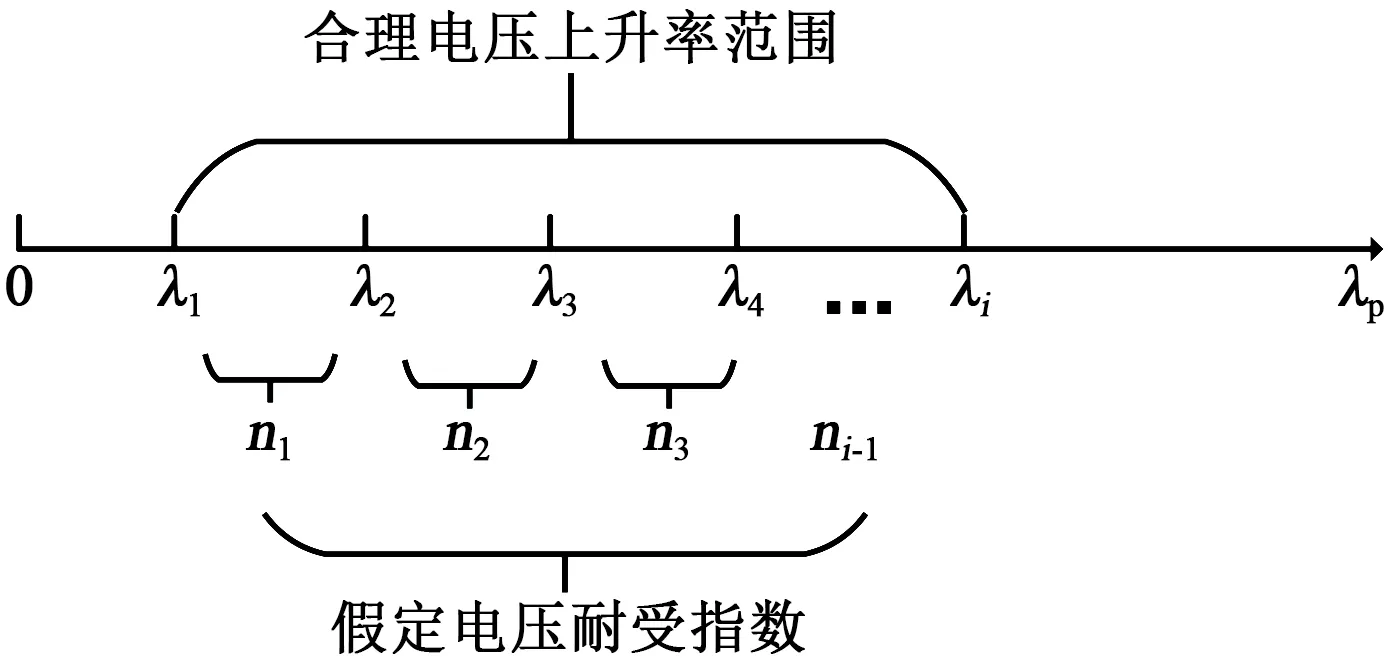
图4 最优试验参数求取Fig.4 Optimal test parameters

将该假定电压耐受指数与理论的电压耐受指数范围进行对比。若该假定电压耐受指数最为接近理论值范围，则该电压上升率范围的中间值就为最佳电压上升率λp。

采用如下所示方法，可由相邻两个λ数值λ1、λ2求取一个假定的电压耐受指数。电压上升率λ1、λ2下的累积损伤为式（9）。

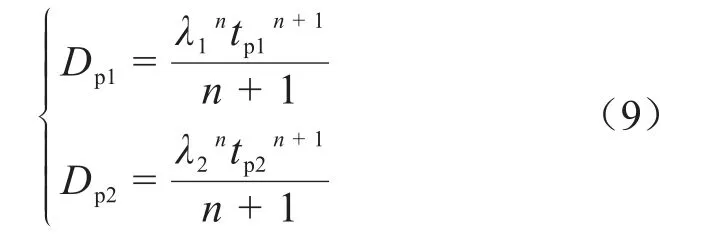
当进行序进应力试验时，可以求得两种电压上升率下的样品寿命tp1、tp2。假定一个电压耐受指数n值，代入式（9）可以求得两种电压上升率下的累积损伤量Dp1、Dp2。基于假设②，假定的n值和累积损伤Dp1、Dp2都满足反幂模型，将它们分别代入式（2）中并取对数得到式（10）。

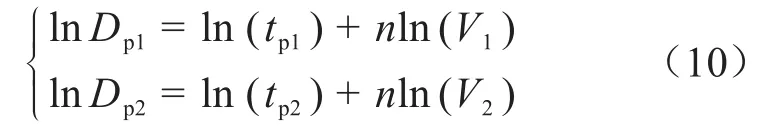
式（10）中，V1、V2为不同电压上升率下序进应力试验等效为恒定应力试验的电压。

将式（10）中两等式代表的直线在双对数坐标系中表示，如图5所示。

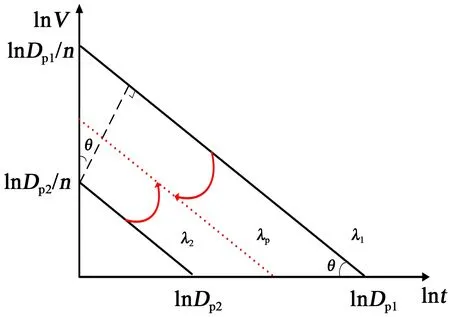
图5 序进应力V-t曲线Fig.5 Progressive stress V-t curves

由图5可知，直线的斜率由假定的电压耐受指数n决定，两条直线保持相对平行的位置关系。然而，每条直线在坐标系中的具体位置是由累积损伤量D所决定的。由于样品都选自同一材料且大小形状相同，在理论上，当假定的n值为XLPE样品电压耐受指数的真实值时，不同电压上升率下电缆击穿时的累积损伤Dp1、Dp2应该相同。但是在真实试验中，累积损伤量存在一定的差异。因此可认为当两条直线越接近时，n值就越接近于该λ范围下电压耐受指数的真实值。由几何关系可知，两条直线斜率相同时，它们之间的距离就可表示直线的差异程度。图5中两条直线之间的距离d可由式（11）表示。

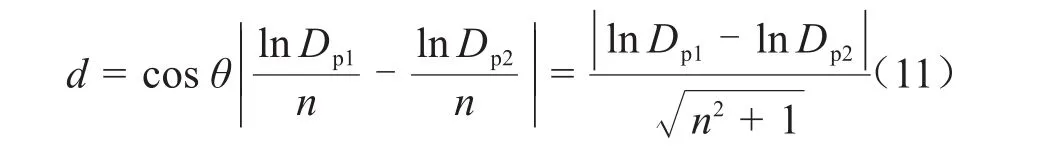
换言之，求取两种电压上升率范围下假定电压耐受指数的问题就可以转化为求取以n为变量，式（12）为目标函数的数学规划问题。

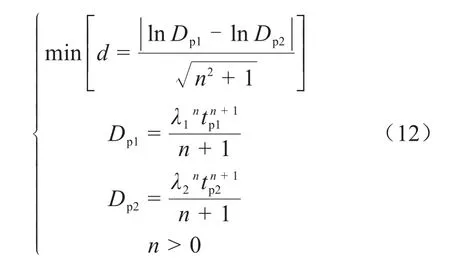
当n值变化时，两条直线相向运动，相交后分开，运动轨迹如图5所示。距离d的大小与Dp1和Dp2差的绝对值呈正相关，在运动过程中先减少至0后再增大。运动过程中两条直线始终保持平行，二者运动的时间和速率近似相等。当两直线运动到中间位置时相交，d达到最小值，此时该位置对应的λp为该范围下最佳的电压上升率，其值为（λ1+λ2）/2。

若选取计算的电压上升率λ数目为m个，求取序进应力试验最佳电压上升率λp的流程如下：

首先，选取一个合理的电压上升率区间，在该区间内选取m个呈等差数列排布的电压上升率（m为偶数）。然后，在该区间内用所有被选λ对a个样品进行序进应力试验得到击穿时间，并计算a个击穿时间的平均击穿时间。最后，再进行相邻两个电压上升率范围内的假定电压耐受指数求取，得到n1、n2…nm-1。将所有不同范围下求得的电压耐受指数与理论的耐受指数范围进行对比，取最接近理论值的电压上升率区间的中间值为序进应力试验最佳的电压上升率λp。

2.2 方法验证

设计不同电压上升率的序进应力试验，进行最佳电压上升率的求取。试验中采用北欧化工公司生产的型号为LS4258DCE的XLPE材料，利用平板硫化机热压制成直径为50 mm、厚度为0.1 mm的圆形薄片作为试验样品，然后用无水乙醇清洗，在60℃真空烘箱中干燥24 h。

为了确定一个合理的序进应力试验电压上升率范围，需要知道样品大致的击穿电压区间。将样品放置在绝缘油内，控制油温为室温，对6组厚度为0.1 mm的XLPE薄片进行短时击穿试验来确定击穿电压区间，初始电压设置为0 kV。记录的击穿电压如表1所示。从表1可以看出，短时击穿试验的击穿电压分布在20～40 kV，为了方便控制电压和保证击穿时间的裕度，合理电压上升率范围取0～2 kV/s。

表1 短时击穿电压Tab.1 Short-term breakdown voltage

设计序进应力试验初始电压V0=0 kV，电压上升率λ分别取0.5、1.0、1.5、2.0 kV/s，每组试验对6个XLPE样品进行击穿。分别记录每组试验所有样品的击穿时间并计算平均击穿时间，结果如表2所示。

根据表2的数据和式（12），对所有电压上升率范围内的假定n值进行计算，计算结果如图6所示。从图6可以看出，在λp取值1.0～1.5 kV/s时，计算得到的假定n值（11.27）接近文献[11]评定的电压耐受指数区间12～16，因此序进应力试验的最佳电压上升率λp为 1.25 kV/s。

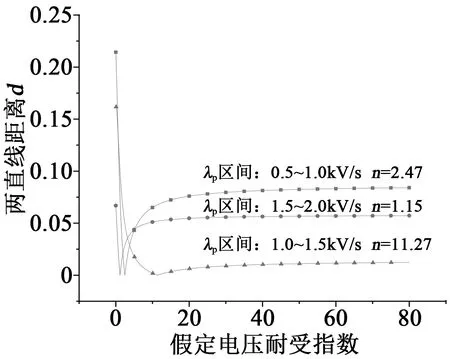
图6 假定n值的计算Fig.6 Calculation of assuming n value

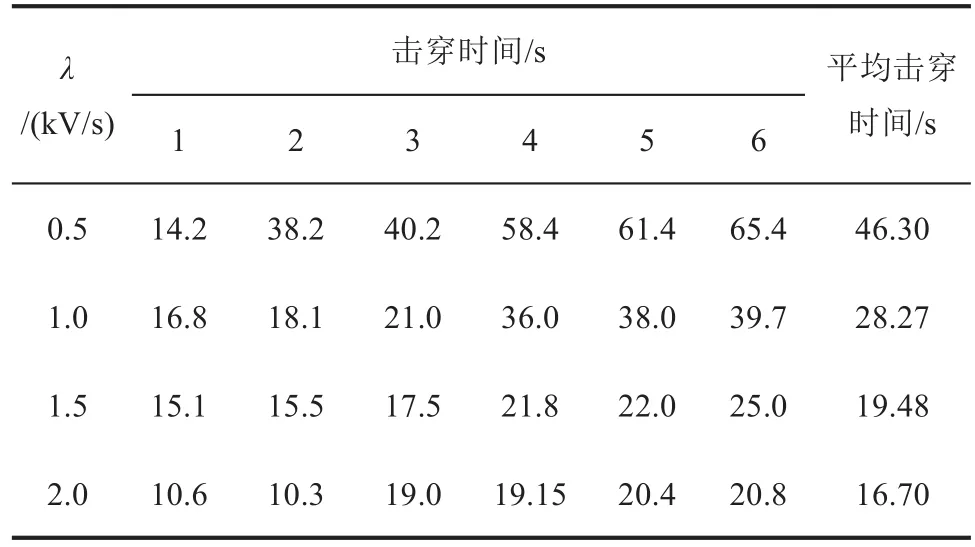
表2 序进应力试验击穿时间Tab.2 Progressive stress test breakdown time

3 混合应力法求XLPE样品n值的试验验证

采用混合应力试验求取XLPE样品的电压耐受指数n。为了验证方法的可行性，采取恒定应力试验进行对照。

3.1 装置搭建

为了减少试验时间，搭建多电极击穿试验装置如图7所示，由多电极加压罐、固态继电器、电磁铁、击穿计时计数器组成。

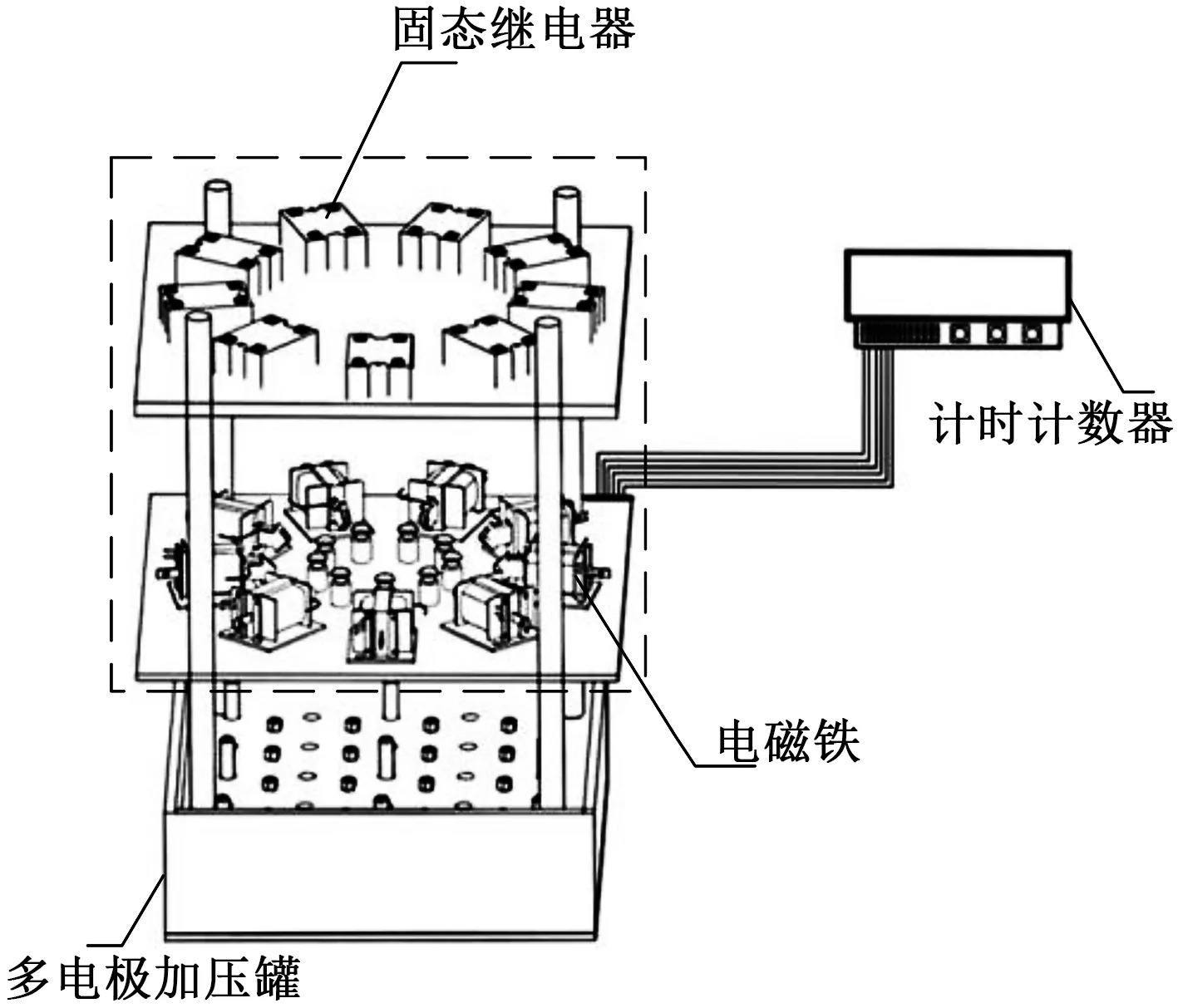
图7 多电极试验装置示意图Fig.7 Schematic diagram of test device with multiple electrodes

多电极加压罐中电极孔呈棋盘排列，单个孔可防止该电极与罐中的接地钢板之间的放电。将多个电极分别置入不同孔位，控制相邻电极之间的距离防止电极间放电。罐中形成一个密闭的空间，并在空间内注入绝缘油，可保持试验时罐中油体的温度，防止异物流入造成试验干扰和阻止闪络的发生。交直流控制电路中的交流电路和直流电路通过电磁铁和固态继电器进行相互控制通断。击穿计时计数器由STM32型微处理器中的实时时钟RTC、存储芯片AT24C02和液晶显示模块组成，用于记录击穿时间。该装置结构简单可靠，可同时进行多组击穿试验，并准确记录各个样品的击穿时间，能够防止装置的误动和拒动，并且能有效防止高压试验时电极间放电现象和闪络的发生。

3.2 求取电压耐受指数

为了方便与恒定应力试验求取的电压耐受指数进行对比，混合应力试验中恒定应力试验部分施加与文献[11]相同的恒定电压，分别为8、9、10 kV。由文献[17]可知，当XLPE失效时间为1 h到1年内，样品失效机理为电热击穿，获取的n值能够保证一定的安全裕度，因此选取恒定应力施加时间为1 h。

设计3组混合应力试验，每组试验放置6个样品。其中恒定应力部分的电压分别为8、9、10 kV，施加时间为1 h，序进应力试验的电压上升率λp为1.25 kV/s。按照样品击穿时间的先后顺序，依次记录每段应力的作用时间，通过式（7）将首、尾两段序进应力作用时间转换为等效恒定应力时间。将等效恒定应力时间与恒定应力作用时间相加得到混合应力时间，试验数据如表3～5所示。

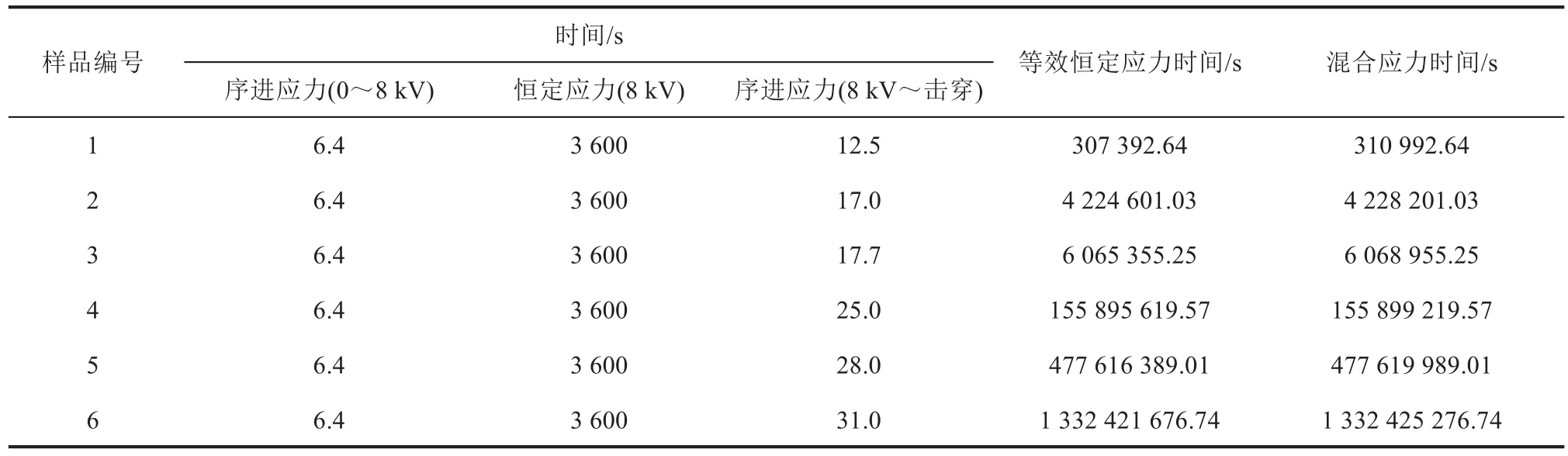
表3 8 kV恒定应力下的混合应力试验时间Tab.3 The mixed stress test time at 8 kV of constant stress

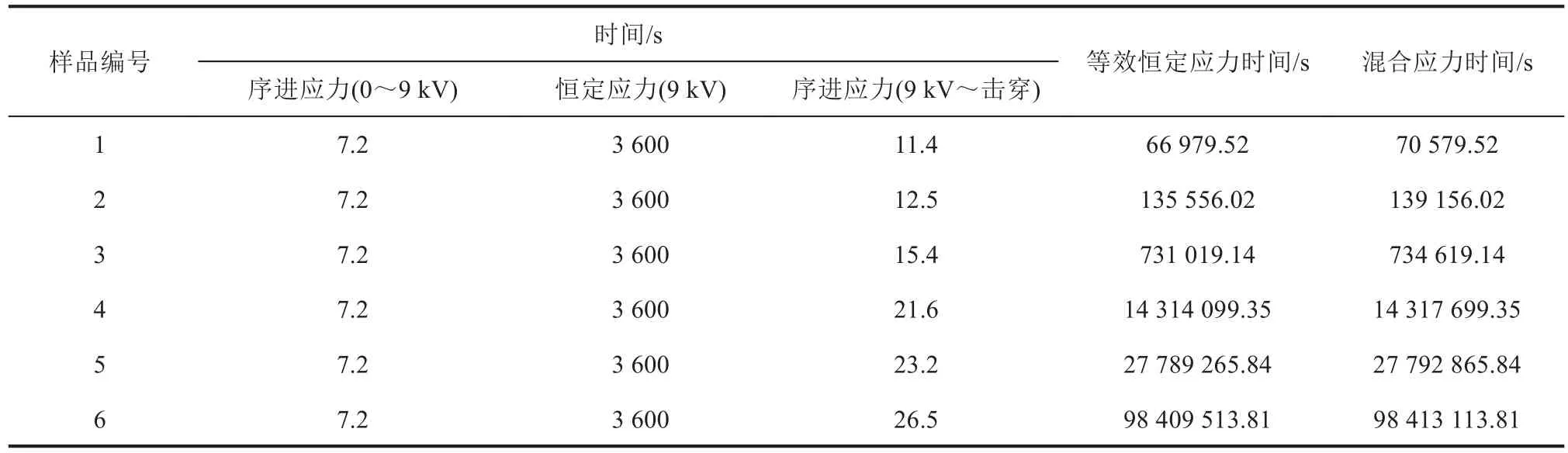
表4 9 kV恒定应力下的混合应力试验时间Tab.4 The mixed stress test time at 9 kV of constant stress

以不同混合应力下击穿时间的对数lnt为x轴，以累积击穿概率F(t)的相关函数ln(-ln(1-F))为y轴拟合直线，结果如图8所示，得到3个混合应力下的Weibull尺度参数分别为18.79、16.23、13.24。

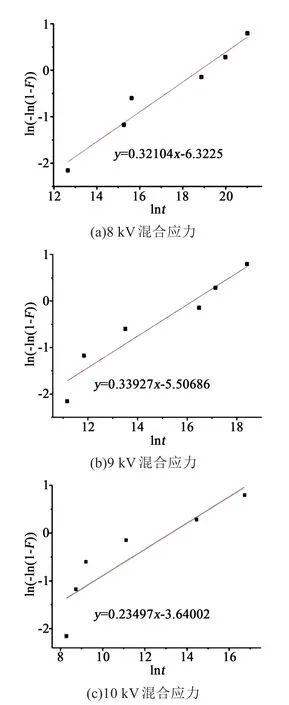
图8 不同混合应力下击穿时间的Weibull分布Fig.8 Weibull distribution of breakdown time at different mixed stress

将3个混合应力等效场强和Weibull尺度参数代入场强和电压组成的双对数坐标轴，线性拟合结果如图9所示。

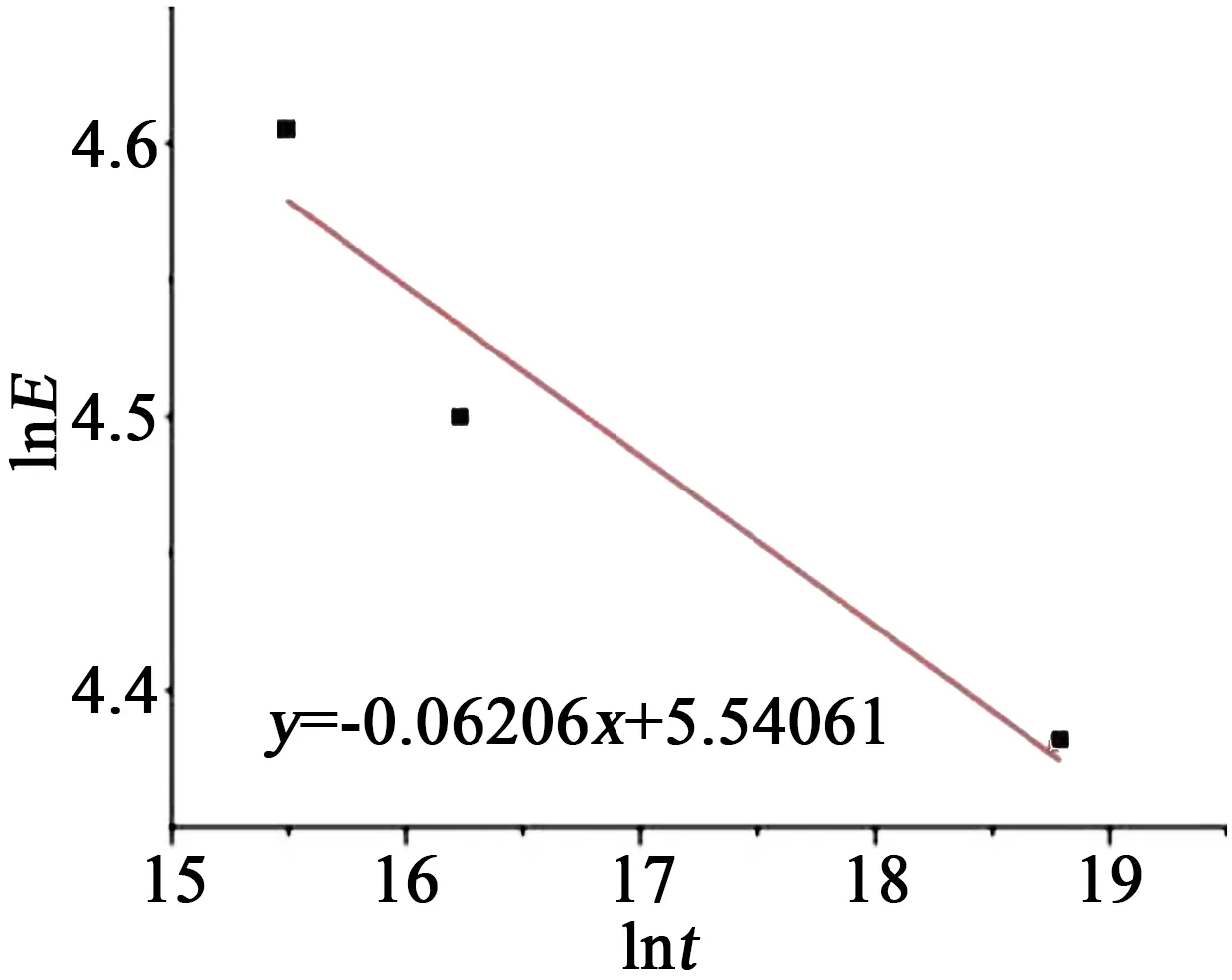
图9 混合应力试验E-t曲线Fig.9 E-t curve of mixed stress test

为了验证方法的正确性，进行恒定应力对照试验。对相同批次和数量的样品分别施加8、9、10 kV的恒定电压进行老化击穿，依次记录击穿时间。将击穿时间拟合，得到3个恒定电压下的Weibull尺度参数，最后将恒定场强和尺度参数代入场强和电压组成的双对数坐标轴，试验结果如表6和图10所示。

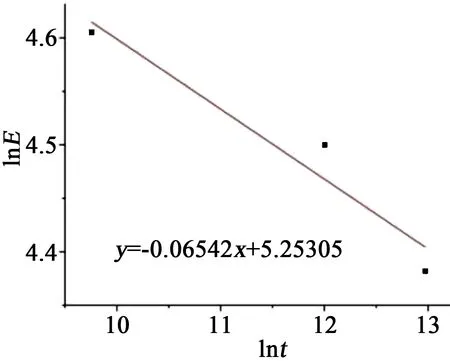
图10 恒定应力试验E-t曲线Fig.10 E-t curve of constant stress test

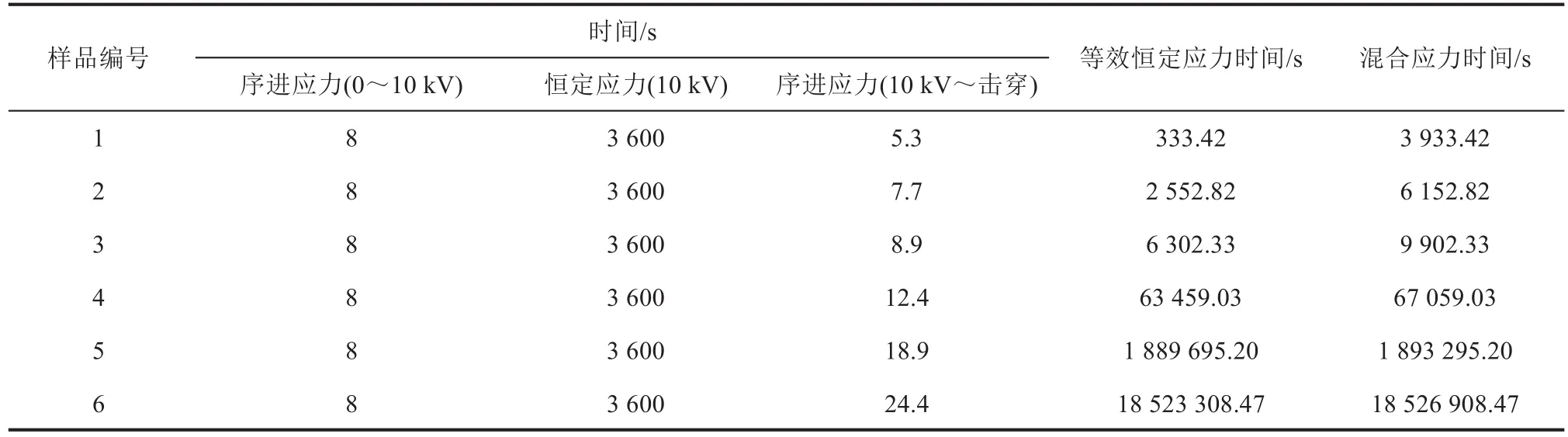
表5 10 kV恒定应力下的混合应力试验时间Tab.5 The mixed stress test time at 10 kV of constant stress

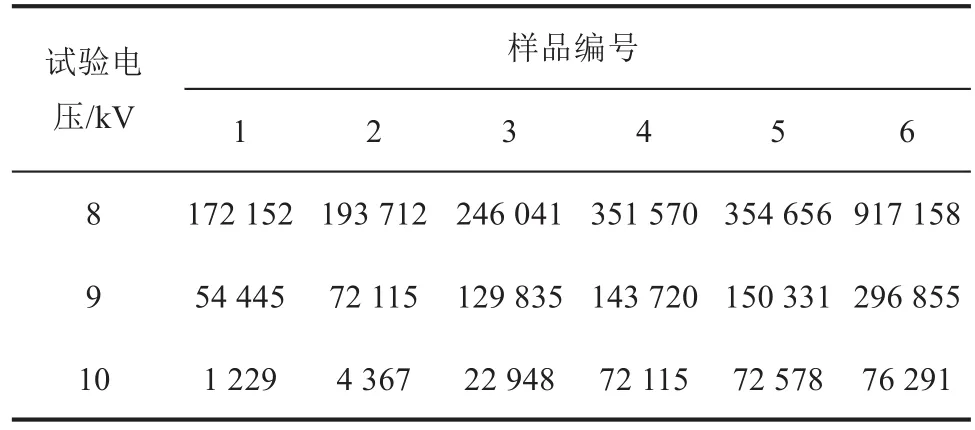
表6 恒定应力试验击穿时间Tab.6 Breakdown time of constant stress test单位：s

计算得到恒定应力试验法评估的电压耐受指数n=15.29，累积损伤D=7.46×1034。混合应力试验耗费总时间为65 249 s，恒定应力试验总时间为3 332 118 s。通过比较，混合应力试验与恒定应力试验评估的电压耐受指数n偏差为5.36%，且混合应力试验总时间比恒定应力总时间缩短了98.04%。

4 结论

根据反幂模型和累积损伤模型证明恒定应力试验和序进应力试验的等效性，依据该等效性提出一种混合应力试验方法并进行验证，主要得到以下结论：

（1）通过不同电压上升率的序进应力试验，得到序进应力试验的最佳试验参数电压上升率λp为1.25 kV/s。

（2）使用混合应力试验对直流XLPE薄片电压耐受指数进行评估，并与恒定应力试验进行比较。试验计算得到电压耐受指数n为16.11，累积损伤D为5.93×1038。所评估n值与恒定应力试验n值的评估值偏差为5.36%，且总时间比后者缩短了98.04%。证明该方法可以有效对XLPE绝缘的电压耐受指数进行评估。