基于多尺度联合置换熵的海洋时间序列同步性研究❋

赵玮奇， 武雅洁,2❋❋， 邹华志， 孙永鑫

(1. 中国海洋大学工程学院， 山东 青岛 266100； 2. 中国海洋大学山东省海洋工程重点实验室， 山东 青岛 266100；3. 珠江水利科学研究院， 广东 广州 510611； 4. 淄博震旦资源环境工程有限公司， 山东 淄博 255000)

海洋系统是一个动态的、复杂的非线性系统，在其演化过程中，研究海洋实测数据的统计学特性能够揭示海洋系统的内在作用机理。风生流是由风作用于海面而产生的切应力引起的海水流动，海表面附近的风向往往会对表面流向产生较大的影响，而研究实测数据中表面流方向与风向之间的关系，有利于深入分析非理想条件下二者相互作用的机制。

近年来，国内外学者对多尺度熵、置换熵进行了大量的研究，并取得了一些成果。Costa等[1]于2002年开发了基于样本熵的多尺度熵(Multiscale entropy, MSE)算法，它在生理信号、脑电信号、振动信号等信号的复杂度分析中起到了重要的作用[2-4]。置换熵(Permutation entropy, PE)是一种基于Shannon熵[5]的度量时间序列复杂度的方法。在实际应用上，PE通常适用于混乱的、嘈杂的时间序列，已经被广泛应用于心电图分析[6]、金融数据分析[7]和交通时间序列分析[8]中。研究两个时间序列同步性的时候，亦可使用置换熵进行分析。受到联合概率分布的启发，可以得到联合置换熵[8](Joint permutation entropy, JPE)，在此基础上再结合多尺度分析，可以得到多尺度联合置换熵[9](Multiscale joint permutation entropy, MJPE)，它可以从次序模式识别和多尺度这两个角度来检测两个复杂时间序列之间隐含的特性。

对于海洋实测数据，赵丹枫等[10]构建了motif规则树，实现了海洋时间序列间强关联规则的挖掘。赵彦平等[11]采用了混沌时间方法对海杂波进行了分析和预测，提高了模型的精确性。徐丽丽等[12]基于赤潮的月发生次数的多年统计资料，建立了以数据驱动为核心的赤潮预测模型。宋大德等[13]利用ARIMA模型对小黄鱼单位捕捞努力量渔获量值进行了验证，与实测值拟合良好。对于风生流实测时间序列的同步性，目前尚缺乏研究。

本文利用多尺度分析的方法，采用多尺度联合置换熵，利用对数变换构建了DI指数，然后构建了同步性指数Isync和同步性指标α，对模拟时间序列和实测时间序列的同步性进行分析，利用实测数据的统计学分析来揭示珠江口区域天文潮的涨落对风生流产生的影响。

1 时间序列的数据

1.1 模拟时间序列

为了测试多尺度分析法对于时间序列的适用性，本文采用的模拟时间序列第一部分为若干个初等函数的组合，分别为二次函数与二次函数、二次函数与三次函数、三角函数与三角函数的组合，横坐标对应的时间分辨率为0.1 s，时间跨度为1～20 s。第二部分为一维Logistic映射，定义为：

xn+1=kxn(1-xn)。

(1)

由一维Logistic映射的性质可知，参数k在3.45和3.56之间时，即存在周期性，又存在混沌，且k越大，混沌程度越大。因此，对参数k分别取3.5、3.51和3.55生成三个序列，所有序列的初始值给定为x1=0.4。

1.2 实测时间序列

本文分析所采用的实测数据来自珠江河口邻近海域的三个测站，每个测站的数据均为单一浮标的实测风向时间序列和实测表面流向时间序列。三个测站的地理位置如图1所示，三个测站的数据基本情况如表1所示。

图1 各个测站在珠江口的位置Fig.1 Locations of all the stations in the Pearl River Estuary

表1 三个测站数据的各项参数Table 1 Parameters of the data of the three stations

2 研究方法

2.1 多尺度联合置换熵(MJPE)

多尺度联合置换熵[8]为多尺度置换熵[14]的二维形式，其构造方法为：

(1)给定时间序列{xt,t=1,2,…,N}和{yt,t=1,2,…,N}，其中N是时间序列的长度。

(2)

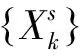
(2)嵌入维数等于3时，对于每一个Z，都对应着图2中的6种子模序，所以计算联合概率时，存在d!×d!种可能的情况。

图2 当嵌入模数为3时的6种模序Fig.2 The six motifs when the embedding dimension is three

JPE同样由Shannon熵定义：

JPE(d,τ)=

(3)

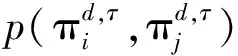
(4)

式中：mts(·)表示由模序空间到符号空间的映射，‖·‖表示集合的基数。当所有的模序组合等概率出现时，JPE具有最大值ln(d!×d!)；当仅有一种相同的模序出现并重复时，JPE有最小值0，即JPE的取值范围是[0, ln(d!×d!)]。

为了后续计算方便，将JPE按照最大值进行归一化：

(5)

(3)由于两个时间序列之间存在相关性，因此可以定义不相关性指数IRRI[8]如下：

(6)

IRRI的定义决定了它的取值范围是[0,1]。此外，每给定一个尺度s，都能得到一个JPE和IRRI，从而可以得到s-MJPE曲线和s-IRRI曲线。通过比较式(3)和式(6)发现：MJPE的值越大，序列间的同步性越低；IRRI的值越小，二者的相关性就越低，同步性也越低。

由于PE并未考虑信号的振幅[15]，并且使用方差对置换熵进行加权会增大和凸显原始数据的局部振幅[16]，为了使IRRI的局部波动振幅相对减小，降低局部波动对后续统一计算同步性指数的影响，本文利用对数函数定义新的DI指数，定义如下：

(7)

式中波动参数a>1，且a越大，IRRI的局部波动振幅越小。实践中根据放缩需求通常取大于1的实数即可。在测试2到10之间的整数以后，发现此参数取5时DI指数较为稳定。因此，本文中此参数取值为5。

同时DI指数也进行归一化，定义如下：

(8)

2.2 时间延迟和嵌入维数的选择

时间延迟τ≥2时，由于时间间隔过大，可能会引起交叉效应，从而降低置换熵计算的准确度，故而本文中τ取1；在实践中，嵌入维数d通常取3、4、5、6、7这几个整数值[14]。当τ=1时，嵌入维数d直接决定了可能出现的模序数量。此外，在联合置换熵计算时，嵌入维数需满足(d!×d!)≪N，以提高获取可靠的统计结果的概率。因此，在N=337的前提下，只有选择d=3才能满足上述要求。

2.3 同步性指数(Isync)

为了用一个指标来衡量两个时间序列的同步性，将Isync定义为：

(9)

式中：Isync的值越大，两个序列间的同步性越高。综合考虑大尺度区域和小尺度区域的计算结果，采用前20%尺度区间的Isync计算结果和后20%尺度区间的Isync计算结果进行平均，得出最终的用于估计同步性的指标α，即：

(10)

式中αF20%表示前20%尺度区间的计算结果，αL20%表示后20%尺度区间的计算结果。

3 实验和验证

3.1 模拟数据实验与验证

本文先利用Python编程，再将计算结果导入Matlab进行绘图。当程序计算的输入变量是下列函数对应的函数值时，MJPE和IRRI在所有尺度上的结果均为0，此时无法计算Isync的数值。虽然下列函数均为非线性函数，但由于它们在给定的离散定义域里呈现出单调增长的趋势，因此无法计算出相应的MJPE和IRRI，即式(11～13)这些非线性函数的同步性趋势不能通过方法3.1来进行多尺度估计。

(11)

(12)

(13)

但是当程序计算的输入变量是下列非线性函数对应的函数值时，计算结果相比于式(11～13)的几组函数出现了明显的变化。由于大尺度区域(位于66.67%～100%的尺度区间)的计算出现了一定的变异，本次计算中只考虑了计算结果有意义的尺度，并且重点关注小尺度区域(位于前0%～33.32%的尺度区间)的计算结果。

(14)

(15)

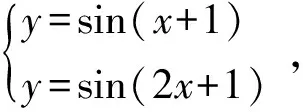
(16)

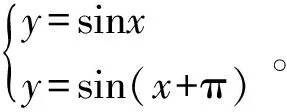
(17)

式中将式(14～17)分别命名为振幅变换、初相变换、相位变换和半周期滞后变换。

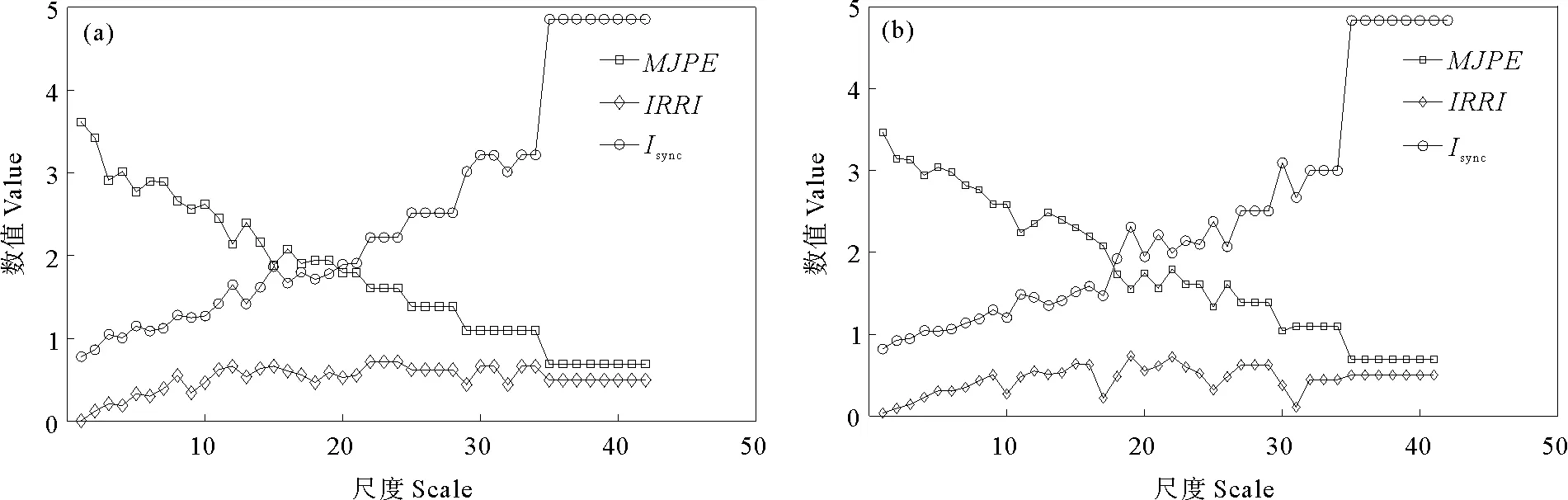
式(14～17)的函数图像如图3所示，4组函数对应的MJPE、IRRI和Isync计算结果如图4所示。

((a)振幅变换;(b)初相变换;(c)相位变换;(d)半周期滞后变换。(a)、(b)、(c)、(d) represents amplitude transformation, initial phase transformation, phase transformation and half-period lag transformation.)

根据上述4组函数的计算结果分析可知(见图4)，MJPE与Isync的变化趋势有关联且恰好相反，即当其中一个增大时，另外一个减小。由于Isync的分子是由IRRI做对数变换得出的，因此IRRI与MJPE和Isync的变化趋势没有明显的关联。Isync在小尺度区域有降低的趋势，然后在更大的尺度范围内逐渐增长并且趋于恒定。

MJPE计算出的随尺度变化的结果能够识别出不同振幅下的同步性、时滞同步性和周期同步性其中，相位变换的MJPE计算结果在小尺度区域明显高于其他3种情况，可认为其在小尺度区域同步性较低，但在大尺度区域却又展现出了与其他3种变换几乎相同的结果。另外，相位变换的IRRI指数在高尺度区域也出现了数值突变，说明在大尺度区域其同步性也表现出了不稳定性。

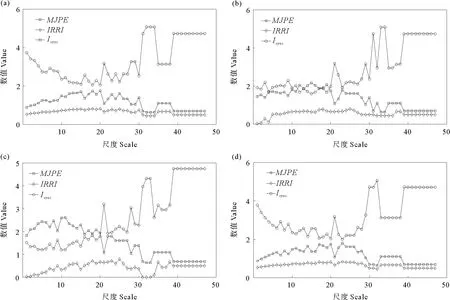
((a)振幅变换的计算结果;(b)初相变换的计算结果;(c)相位变换的计算结果;(d)半周期滞后变换的计算结果。(a) Calculation results for amplitude transformation; (b) Calculation results for initial phase transformation; (c) Calculation results for phase transformation; (d) Calculation results for half-period lag transformation.)

对比振幅变换和初相变换的计算结果，其他3组函数在小尺度区域振幅变换的MJPE较小，IRRI较大，这说明振幅变换在小尺度区域具有更高的同步性；对比振幅变换和半周期滞后变换的计算结果，二者在中尺度区域略有分歧，几乎没有明显的差异；初相变换和半周期滞后变换本质上都是初相变换，半周期滞后变换恰好将函数的最大值对应的自变量数值和最小值对应的自变量数值平移到了同一点，二者的MJPE和IRRI的计算结果显示半周期滞后变换在小尺度区域的同步性更高。

4种变换对应的同步性指标α的计算结果如表2所示。可以看出，振幅变换的同步性指标最高，半周期滞后变换次之，相位变换最低。表中的数据说明四种变换对应的同步性可以进行量化分析和比较。

3个Logistic映射序列如图5所示。对图6、7的计算结果进行比较分析，发现参数k的取值越大，Logistic序列的周期越大，混沌程度也越高，因此混沌程度的相对大小为Logistic3>Logistic2>Logistic1。由3组Logistic映射的计算结果可以看出，MJPE、IRRI和Isync呈现出了一定的跳跃性，局部突变比较明显。Logistic1与Logistic2的同步性指数α更高，意味着两个时间序列的同步性和相似度也更高，这符合Logistic序列的变化特点。对Logistic序列的分析结果说明，此方法在同步性的识别上有一定的效果。

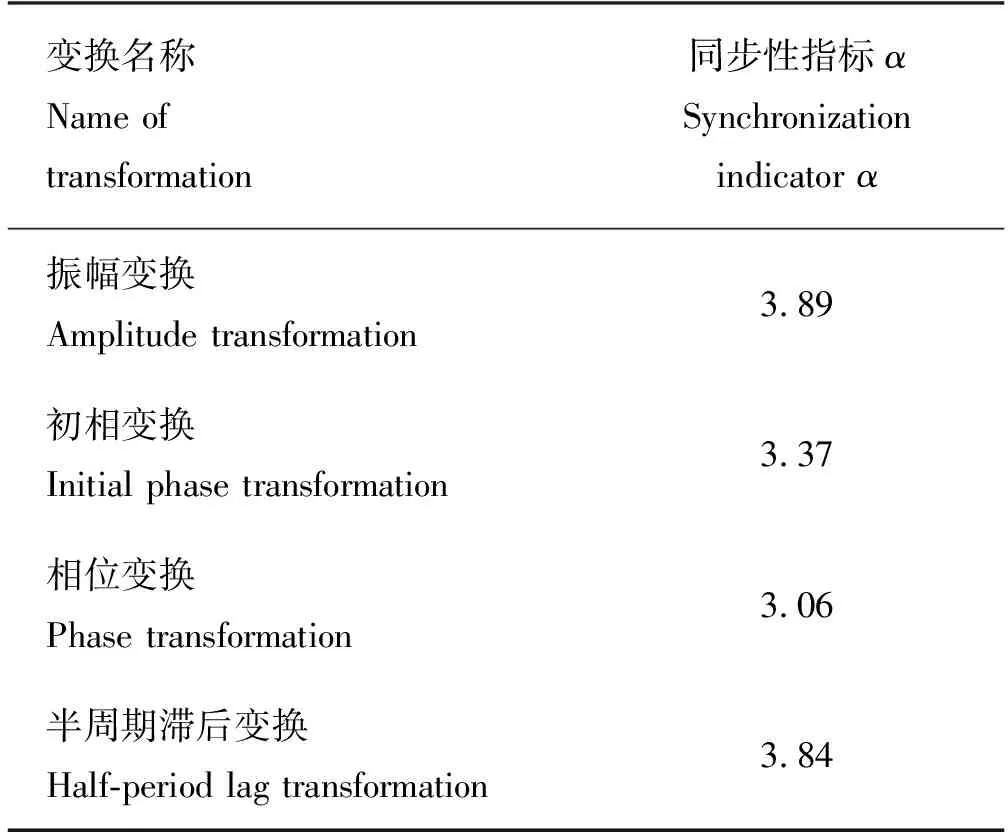
表2 四种变换对应的同步性指标α的计算结果(保留两位小数)

图5 三个Logistic映射序列的示意图Fig.5 Schematic diagrams of the three logistic map series

图6 Logistic 1与Logistic 2的MJPE、IRRI和Isync计算结果Fig.6 MJPE,IRRI and Isync results for the total wind directions and total sea surface velocity directions of Logistic 1 with Logistic 2

图7 Logistic 1与Logistic 3的MJPE、IRRI和Isync计算结果Fig.7 MJPE,IRRI and Isync results for the total wind directions and total sea surface velocity directions of Logistic 1 with Logistic 3

3.2 实测数据实验与验证

3.2.1 总体数据的计算分析 根据1号测站2018年10月25日—11月1日的实测数据，得到实测风向与表面流向的总体MJPE、IRRI和Isync的计算结果如图8所示。结果表明：当尺度大于50时，计算结果没有明显的变化，这是由于MJPE在大尺度区域的计算具有不稳定性或者变异性。对于1号测站2018年11月1—8日的实测数据，如图9所示，在尺度70以内的MJPE、IRRI和Isync计算结果走势良好。

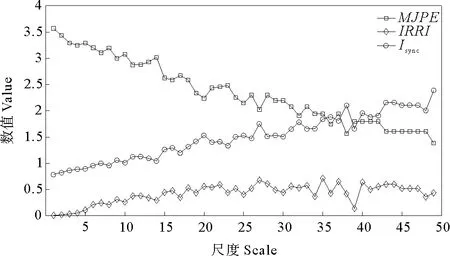
图8 1号测站2018-10-25—2018-11-01实测风向与表面流向的总体MJPE、IRRI和Isync计算结果Fig.8 MJPE,IRRI and Isync results for the total wind directions and total sea surface velocity directions of station 1 during the period from October 25th,2018 to November 1st,2018

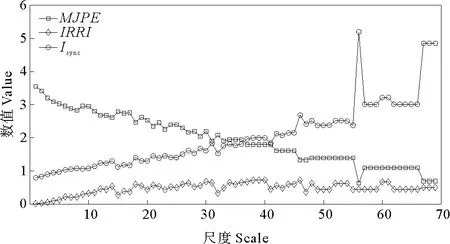
图9 1号站2018-11-01—2018-11-08实测风向与表面流向的总体MJPE、IRRI和Isync计算结果Fig.9 MJPE,IRRI and Isync results for the total wind directions and total sea surface velocity directions of station 1 during the period from November 1st,2018 to November 8th,2018

由图8～9的计算结果可以看出：(1)在小尺度区域MJPE和IRRI没有明显的同步性变化趋势差异，但是在大尺度区域却有明显的差异，IRRI在不同的尺度区域表现出了明显的波动，证明了进行多尺度研究对于识别实测数据同步性的必要性。(2)表面风向和表面流向的同步性指数在小尺度区域随着尺度的增大而增大，但是在大尺度区域，由于数据包裹导致的变异，两个不同时段的MJPE、IRRI和Isync计算结果表现出了分歧，表明在小尺度区域和大尺度区域的MJPE、IRRI和Isync计算结果受到数据包裹的影响也不同，大尺度区域更容易受到数据包裹的影响。

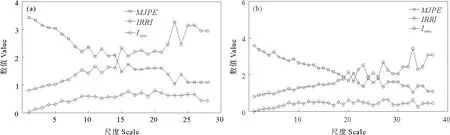
3.2.2 涨落潮数据计算分析 由于天文潮的涨落潮切换会影响表面流向，使用Matlab的TMD(Tidal Model Drive)工具箱推算出各测站在相应时间段的潮位过程线，再分析各测站落潮、涨潮期间风向和表面流向的MJPE、IRRI和Isync计算结果，如图10、11所示。3号测站和4号测站与1号测站的计算结果类似，不再具体展示计算结果。

((a)落潮期间的计算结果;(b)涨潮期间的计算结果。(a) Calculation results for the ebb period; (b) Calculation results for the flow period.)图10 1号站2018-10-25—11-01落潮、涨潮期间的MJPE、IRRI and Isync计算结果Fig.10 MJPE,IRRI and Isync results for the total wind directions and total sea surface velocity directions of station 1 during the ebb period and flow period from October 25th,2018 to November 1st,2018

((a)落潮期间的计算结果;(b)涨潮期间的计算结果。(a) Calculation results for the ebb period; (b) Calculation results for the flow period.)图11 1号站2018-11-01—08落潮、涨潮期间的MJPE、IRRI and Isync计算结果Fig.11 MJPE,IRRI and Isync results for the total wind directions and total sea surface velocity directions of station 1 during the ebb period and flow period from November 1st,2018 to November 8th,2018

对涨落潮数据进行分离，对比图10、11可以看出，同一测站在同一时间段的MJPE、IRRI和Isync计算结果的走势除个别突变以外基本一致。因此，仅从MJPE、IRRI和Isync计算结果来看，1号测站在涨落潮期间风对表面流向的影响基本一致，3号测站和4号测站亦如此。

3.2.3 同步性指标α的计算分析 通过对1号测站同步性指标α的计算结果进行分析比较(见表3)，结果表明整体上实测的同步性指标α数据相比模拟数据明显偏低。这是由于实测数据的测量扰动因素多，并且受初始条件影响大，导致了数据具有更高的复杂度和更高的混沌程度。

总体数据的计算结果明显低于涨落潮分离以后的计算结果，进一步证明了涨落潮分离计算的必要性。由表3可以看出，1号测站的同步性指标α在两个不同的时段均出现了落潮>涨潮>总体的趋势。3号测站和4号测站的计算结果亦如此，不再赘述。

1号测站在两个时段的同步性指标α计算结果如图12所示，可以看出：落潮期间同步性指标整体更大，落潮期间比涨潮期间的同步性指标α计算结果偏大4.9%到7%，这与3号测站和4号测站的计算结果一致。从同步性指标α统计结果上来看，各个测站在落潮期间风应力对表面流向的影响更大。总体数据的同步性指标α计算结果明显偏低，可能是因为涨落潮切换时由于受到下层海水阻力的影响，表面流向的反转需要一定的时间，导致实测数据出现一定的时间滞后性。

表3 三组数据对应的同步性指标α的计算结果(保留两位小数)

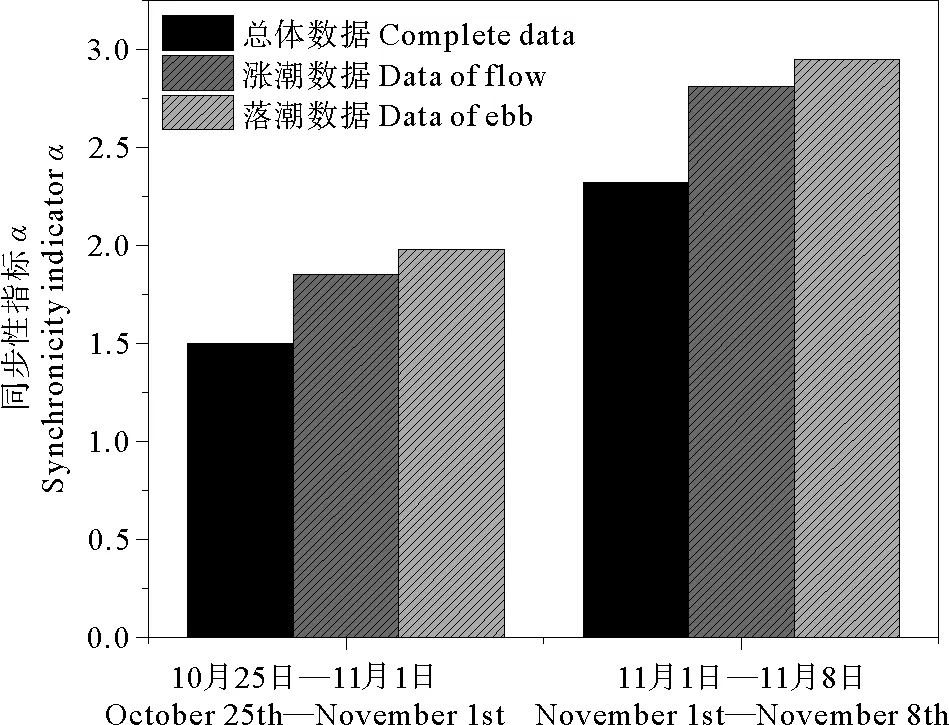
图12 1号测站的同步性指标α计算结果Fig.12 Synchronization indicator α results for station 1

4 结论

本文提出了衡量同步性的同步性指数Isync和同步性指标α，在此基础上，结合多尺度联合置换熵来分析模拟时间序列间的同步性和实测海洋时间序列间的同步性。本文得到的结论包括以下三个方面：

(1)在前人研究成果的基础上，把对时间序列本身进行变换，改成对IRRI做类似对数变换的一种变换后再进行归一化，进而提出了同步性指数Isync和同步性指标α的一种计算方法，尝试把多尺度分析统一到一个指标中。

(2)应用了MJPE、IRRI和同步性指数Isync和同步性指标α，计算并分析了4组初等函数和2组混沌系统的同步性，证明了多尺度分析的必要性，并认为Isync和α能够识别时滞同步性和周期同步性，但是Isync在大尺度区域的计算结果可能会有不稳定和变异。此外，同步性指标α能够综合考虑Isync在大尺度区域和小尺度区域的计算结果。

(3)应用上述指标计算并分析了三个测站不同时间段的实测风向时间序列和实测表面流向时间序列，同样证明了多尺度分析的必要性。此外，对涨落潮分离以后的数据进行分析，有助于判断出在涨潮、落潮期间风对表面流向的影响。针对实测数据的分析发现，落潮期间同步性指标α更大，即落潮期间风应力对表面流向的影响更大。

综上所述，这种方法不仅对于研究风应力对表面流向的影响有指导意义，且对于研究模拟时间序列的同步性和实测时间序列的同步性的方法也有改进，但同步性指标α的结构略显简单，因此后续研究中可对同步性指标α的定义进行改进。