绿色风险投资抑制了碳排放吗？——基于绿色技术创新视角的实证研究

邵兴宇，范德胜

(1.中国社会科学院大学 经济学院， 北京 102488； 2.北京外国语大学 国际商学院， 北京 100081)

一、引言

改革开放40多年以来，我国经济飞速增长，但高投资、高能耗和高排放的粗放型增长方式也让我们付出了巨大的环境代价，环境问题已然对我国长期可持续发展形成资源和环境约束。在这种情况下，2020年9月，习近平主席在第75届联合国大会一般性辩论上向全世界做出“碳达峰”和“碳中和”的庄严承诺，这一承诺无疑向全世界展现了我国实现经济绿色发展的决心和雄心。

碳减排目标的提出意味着经济社会向绿色低碳转型，而绿色技术创新正是推动这种转型的基础和关键。与此同时，绿色革命作为新一轮的技术革命，其发展也同样离不开金融资本的支持。易纲认为绿色金融的重点在于通过“市场+政府支持”的机制，动员更多私人、民营资本加入绿色产业的融资行为[1]。绿色风险投资是社会各界积极应对环境变化、推动绿色技术发展的重要抓手。据新浪科技报道，由比尔盖茨等科技大亨发起的风险投资计划已经完成对45家创业企业共计10亿美元的投资，专门用于清洁能源技术开发。在国内，绿色技术也同样是风险投资的热门领域。但是与实践相比，目前学界对于绿色风险投资的研究还十分匮乏。那么绿色风险投资能否降低碳排放？绿色风险投资又是否促进了绿色技术进步？这正是本文尝试解答的问题。

二、文献综述及研究假设

(一)绿色风险投资与碳排放

现有研究将绿色领域定义为：以知识为基础的，能够改善操作业绩、提高生产力、增加效益，同时减少成本、原料、能源消耗、废物及污染的任何一种产品或服务。广义讲，绿色领域包括所有能够减少废物，提高效益的科技、创新、产品、生产方式等等[2]。所谓的绿色风险投资，指的就是投向绿色领域的风险投资。从理论上看，绿色风险投资与绿色产业存在天然契合。不同于传统污染型企业，环境友好型企业代表了未来绿色发展的方向，有相当比例正处于初创阶段，运营能力往往还不够成熟，具有成长阶段企业的普遍特征[3]。在现有文献中，作为绿色金融的一个重要组成部分，绿色风险投资也被普遍认为架起了金融资本与绿色企业之间合作的桥梁[4]，并直接促进了碳排放的减少[5]。

具体来讲，一方面，绿色风险投资的引入增加了绿色行业金融资源供给，并通过促进绿色产品供给扩大，实现碳排放减少[6]。绿色风险投资本身就是绿色金融的一种形态，作为一种金融资源，其加大投入直接促进了绿色产品的供给[7]。与此同时，绿色风险投资对绿色行业的金融支持也带来了“信号”效应。由于风险投资往往要求较高的回报率，风险投资的介入往往意味着被投资企业表现出健康的运行状态。绿色风险投资向绿色行业的投资可以被视为一种“信号”，吸引更多其他资本形式流向绿色行业，从而进一步放大对碳排放的影响[8]。

假设1：在其他条件相同的情况下，绿色风险投资与单位碳排放呈负相关关系，即随着绿色风险投资提高，碳排放水平降低。

(二)绿色风险投资与绿色技术创新

在经典理论当中，关于金融与技术创新之间关系的研究已经相当多，一系列研究总体上认为金融加快了技术创新的进程[9]。近年来兴起的绿色革命很大程度上也是由绿色技术创新推动的。绿色创新被定义为有助于提高环境可持续性的创新，是防止环境恶化的重要战略[10]。然而，绿色创新需要长期的战略投资和大量的资金支持[11]。风险投资提供资金和资源，且投资周期往往较长，因此在促成绿色技术创新上扮演了重要角色[12]。具体来看，绿色风险投资至少在3个层面促进了绿色技术创新：

第一，引入绿色风险投资缓解了融资约束，为创新提供了资金支持。通常来讲，创业企业往往具有经营不稳定、风险较高等特征，且往往缺乏足值抵押物，因此导致企业在传统融资模式下难以获取金融支持。风险投资本身就具有风险偏好较高的特点，其投资着眼于企业未来的发展前景而非企业固定资产，通过提供资金推动企业进一步创新[13-14]。

第二，引入绿色风险投资有助于完善公司治理结构，为创新提供组织支持。创业企业通常缺乏相关资源和商业经验，内部组织架构不健全，公司治理结构不完善，极大制约了技术研发[15]。对风险投资而言，投资人与被投资企业之间形成了委托代理关系，有必要强化对被投资企业的监督。与此同时，风险投资本身也寄希望于通过被投资企业的稳步发展来推动完成IPO，从而获得较高收益并顺利退出，而这也要求风险投资主动改善被投资企业公司治理结构[16]。

第三，引入绿色风险投资为创新搭建了信息交流的平台，为创新提供了平台支持。通过风险投资机构所构建的网络，创业企业可以从外界获取资金、信息、知识、技术、信任等发展所必需的资源[17]。

基于以上研究情况，本文提出如下假设：

假设2：在其他条件相同的情况下，绿色风险投资与绿色技术创新呈正相关关系，即随着绿色风险投资提高，绿色技术进步水平提高。

(三)绿色技术创新与碳排放

绿色技术创新作为实现生态文明和绿色转型的关键途径,与其他技术相比更具创新性和可持续性。人们很早就注意到技术创新在实现碳减排中的作用，1992年联合国举行的环境与发展大会中通过了《21世纪议程》,其中就明确强调了绿色技术的重要性[18]。技术进步同样也是我国近年来碳排放减少最为重要的推动力量[19]。绿色技术水平的提高直接提升了现有能源的利用效率，绿色技术创新通过现有能源循环利用提高了能源效率，使得单位GDP产出所需要的化石能源大大减少，进而达到了减少碳排放的目的[20]。同时，技术进步也使核能、风能、生物能、地热能等各类清洁能源产出增加，改变了传统化石能源与新兴清洁能源的比价关系，从而使得新能源成为能源供给的潜在替代选项，通过减少化石能源的使用，改变了现有能源结构[21]。更重要的是，绿色技术创新的诞生和推广改善了绿色产品供给，率先实现绿色技术进步的行业因其在高技术要素含量等方面的优势，自身获利能力增强，进而对产业结构产生影响[22]；同时需求方面，绿色技术也促使绿色产品价格降低，从而改变了传统产品与绿色产品之间的比价关系，由此改善产业结构，并最终实现碳减排目标[23]。

结合假设1和假设2的论证，不难看到绿色风险投资、绿色技术进步与碳排放之间的密切联系。其一，绿色风险投资对碳排放存在直接影响，绿色风险投资通过扩大绿色产品供给和“信号”效应直接促进碳减排；其二，绿色技术创新在绿色风险投资与碳排放之间发挥中介效应，即绿色风险投资通过促进绿色技术创新间接影响了碳排放。因此，本文提出如下假设：

假设3：绿色技术创新在绿色风险投资与碳排放之间发挥了中介效应。

总结上述理论机制分析，我们利用机制路线图(图1)来更加清晰地展示绿色风险投资、绿色技术创新和碳排放三者之间的关系。

图1 理论机制路线

三、数据来源和计量模型设定

(一)变量定义与数据来源

1.核心被解释变量

本文核心被解释变量为碳排放强度的对数值。碳排放强度是碳排放与实际GDP的比值，表示单位产出对应的碳排放量。到目前为止，各省份碳排放强度仍然缺乏官方数据。本文采用联合国政府间气候变化专门委员会(IPCC)提供的方法，根据如下公式计算获得各省份二氧化碳排放强度：

(1)

式(1)中，C是碳排放强度，n表示各类不同能源，参考联合国政府间气候变化专门委员会的研究方法，本文将终端能源消费划分为煤炭、焦炭、汽油、煤油、柴油、燃料油和天然气7种,En为第n种能源消费量，数据来自于《中国能源统计年鉴》，βn为第n种能源碳排放系数，具体数值参考IPCC相关指南[24]，αn是能源的标准煤折算系数，12/44是碳乘数因子。

2.核心解释变量

本文核心解释变量为绿色风险投资规模的对数值。目前国内关于绿色金融的研究大多局限于绿色信贷和绿色债券等，对绿色风险投资研究较为薄弱的一个重要原因是研究数据的匮乏。本文参考江红莉等[7]的研究方法，将绿色风险投资定义为投向新能源、新材料和环保3个行业的风险投资总额，其中新能源包括太阳能、风能和生物能等，环保包括水污染治理、大气污染治理、固废处理利用、环保产品和环境服务等，新材料包括膜材料、环保设备等。绿色风险投资的原始数据来源于清科集团的私募通数据库(PEDATA)，将新能源、新材料、环保3个行业的风险投资额依据风险投资事件发生的年份和被投资企业注册地分别匹配到不同年份和省份，并取对数。

3.中介变量

绿色技术进步。现有研究分别从绿色技术创新的投入、产出和绩效3个维度入手，分别形成了R&D投入、专利申请和获取、全要素生产率三类指标。但是 R&D投资和绿色生产率的获取往往受限于数据可得性，数据质量难以保证。目前看，绿色技术进步最为直接的体现是专利的获得情况，使用绿色专利来评估绿色技术进步具有一定的优势。鉴于此，本文整理了中国知识产权局公布的有效专利申请信息，并结合世界知识产权组织(WIPO)公布的环境友好型技术界定标准，从专利申请信息中筛选出各省份各个年度绿色专利和全部专利申请数据。本文利用专利数据，参考王班班等[25]的研究方法，构造了两类指标：(1)绿色专利申请规模，反映绿色技术创新的规模；(2)绿色专利申请占比，即绿色专利申请量占全部专利申请量的比例，反映技术创新方向。

4.控制变量

考虑到碳排放强度还受到其他众多因素的影响，本文选取如下控制变量：(1) 人均GDP的对数值及人均GDP对数值的平方，用以刻画人均GDP对碳排放可能存在的倒“U”型影响，即环境库兹涅茨假说(EKC假说)；(2) 城镇化率，定义为城镇人口占常住人口的比率；(3) 产业结构，定义为第二产业占GDP的比重；(4) 人口密度，定义为每平方公里人口数的对数值；(5) 贸易开放度，定义为进出口总额占GDP的比重。以上数据全部取自国家统计局官网。

通过以上步骤，整合《中国能源统计年鉴》、私募通数据库、国家知识产权局专利数据等，剔除宁夏、新疆、西藏等样本严重缺失的地区后，获得了28个省份2006—2019年的非平衡面板数据，对上述变量的描述性统计如表1所示。其中，碳排放强度取对数后均值为0.581，同时极值间差距较大，表明我国省级碳排放强度整体偏高且不同区域间差距明显；绿色风险投资规模对数后均值为2.992，即绿色风险投资平均规模仍相对较小，但标准差达到2.075，反映出各省份绿色风险投资发展上存在巨大差异；绿色专利申请规模取对数后同样标准差较大，同时绿色专利申请占比两个极值间差距明显，反映出各省份绿色技术进步水平的不均衡。控制变量方面，人均GDP在样本期间内稳步上升，产业结构均值为0.429，第二产业仍在经济结构中占有较大比重；我国当前城镇化进程稳步推进，但西部地区稍有落后，人口密度取对数后均值达到7.927，反映了我国人口相对稠密的特点，同时也与新疆、西藏等部分西部省份样本缺失有关，贸易开放度东西部之间差距明显。

表1 描述性统计

(二)模型设定

1.散点图

为直观观测绿色风险投资与碳排放强度、绿色专利申请规模和绿色专利申请占比的关系，画出散点图(图2～图4)。从图中不难看到，绿色风险投资与碳排放之间呈负相关关系，而与绿色专利申请规模、绿色专利申请占比均呈正相关关系，即绿色风险投资规模上升可能导致碳排放强度下降，假设1符合散点图直观观察。同时绿色风险投资规模上升促使绿色专利申请规模和申请占比上升，表明假设2也很可能是成立的，但要得到精确的结论还需要进行更严格的实证检验。

图2 绿色风险投资与碳排放强度散点

图4 绿色风险投资与绿色专利申请占比散点

2.模型构建

基于本文提出的研究假设，首先设定如下基准模型：

Ln(C/GDP)it=α0+α1*LnGreenVCit+α2*Controlsit+μi+υt+εit

(2)

其中，下标i代表不同省份，下标t代表不同年份，Ln(C/GDP)it为被解释变量，表示在时期t的第i个省份碳排放强度的对数值。核心解释变量LnGreenVCit为i省份在时期t的绿色风险投资规模的对数值。控制变量组包括人均GDP对数值、人均GDP对数平方、城镇化率、产业结构、人口密度对数值、贸易开放度，αi为待估参数，μi表示个体固定效应，υt为时间固定效应，εit为随机误差项。

同时，为检验假设2提出的绿色风险投资影响碳排放强度的具体机制，本文构建如下中介效应模型：

(3)

(4)

本文采用逐步回归法进行中介效应检验，详细检验过程为：首先对基准方程(2)进行回归，如果核心解释变量系数显著，则表明绿色风险投资对碳排放强度存在总体效应，进一步进行后续检验。其次，以绿色技术水平的j维度(绿色专利申请规模、绿色专利占比)作为被解释变量，检验回归方程(3)，验证绿色风险投资是否影响了绿色技术水平。最后，以碳排放强度为被解释变量，将绿色风险投资与绿色技术水平第j个维度同时纳入模型，检验回归方程(4)。如果回归方程(4)中回归系数δj与回归方程(3)中系数θj同时显著，则表明绿色技术水平第j个维度存在中介效应；若系数δj与系数θj当中至少存在一个变量不显著，则进行Sobel检验；若检验结果显著，则存在中介效应，反之，则不存在中介效应。

四、直接效应分析

(一)基准回归结果

为防止计量结果出现伪回归，在实证开始前先进行了面板数据单位根检验，以检验变量的平稳性。由于使用的数据样本是非平衡面板，采用面板Fisher型单位根检验，检验结果如表2所示，结果显示面板数据平稳，可以对面板进行回归检验。

表2 各变量平稳性检验结果

本文首先使用全样本研究绿色风险投资对碳排放强度的影响。对回归方程(2)进行实证检验，结果报告在表3的(1)～(4)列。表3的(1)列首先报告了不纳入控制变量下核心解释变量绿色风险投资对数值与被解释变量碳排放强度间双向固定效应模型的回归结果。结果显示，对全样本而言，绿色风险投资与碳排放强度呈现负相关。随后(2)列将控制变量组加入回归，同时仍然控制个体效应和时间效应，核心解释变量同样保持1%水平上显著。为了便于比较分析，表3第(3)列～(4)列分别汇报了使用混合最小二乘法(Pooled Least Square)和随机效应模型的回归结果，结果显示，在所有回归结果中，绿色风险投资的估计系数均显著为负，且系数值为-0.319～-0.187。此外，观察控制变量，人均GDP回归系数全部显著为正，且人均GDP的平方项均显著为负，表明对本文样本而言，伴随着人均GDP的上升，碳排放强度先上升后下降，即二者之间呈现倒“U”型，这与现有关于环境库兹涅茨假说的研究是契合的；城镇化率、产业结构和人口密度系数全部为正，这也与现有研究结论保持一致[26]。上述结果说明，绿色风险投资对碳排放强度具有显著负向作用，初步验证了本文的假设1。

表3 绿色风险投资对碳排放的直接效应回归结果

(二)稳健性检验

1.变量替换

为检验上述结果的稳健性，进一步考察绿色风险投资对碳排放强度的影响，首先考虑替换被解释变量，以消除单一变量测度对回归结果产生的潜在影响。本文借鉴胡海峰等[9]及Xiaoyan等[27]的研究方法，用人均碳排放和PM2.5替换碳排放强度，并继续用双向固定效应模型进行回归。其中，人均碳排放定义为各省份当年碳排放总量除以常住人口规模后取对数，PM2.5使用华盛顿大学Atmospheric Composition Analysis Group提供的各省区地表PM2.5年均浓度。回归结果分别汇报在表4的第(1)和第(2)列。从回归结果看，绿色风险投资对人均碳排放和PM2.5的回归系数分别为-0.186和-0.171，与绿色风险投资对碳排放强度的回归系数较为接近，且回归系数均在1%水平下显著。此外，控制变量组与基准回归结果正负号方向及显著性也仍保持一致，这初步证明基准回归结果较为可信。

2.子样本回归

在基准分析的基础上，各省区按照地理位置划分为东中西部地区，并使用双向固定效应模型分别进行回归，以考察绿色风险投资对碳排放强度在不同地区间可能存在的异质性。表4的第(3)～(5)列分别汇报了东部地区、西部地区和中部地区的回归结果。从回归结果看，对不同地区而言，绿色风险投资对碳排放强度的回归系数处于-0.171到-0.197之间，与全样本回归-0.187的回归结果大致接近，且仍然保持1%水平下显著。其中，东部地区回归系数绝对值最小，中部地区最大，这表明绿色风险投资规模上升对中部地区碳排放强度降低的作用作为明显，西部地区其次，东部地区作用最小。

表4 变量替换及子样本回归结果

3.内生性处理

对于本文实证结果的一个担忧来自于变量内生性问题。尽管面板固定效应模型可以在一定程度上解决回归模型存在的内生性问题，但严格的实证结论仍需要对内生性问题进行进一步研究讨论。就本文而言，内生性问题的潜在来源主要是核心被解释变量碳排放强度与核心解释变量绿色风险投资规模之间可能存在的反向因果关系和遗漏变量。为此，借鉴江红莉等[7]的研究思路，在基准模型(1)的基础上，提出如下回归：

Ln(C/GDP)it=α0+ξ*Ln(C/GDP)it-1+α1*LnGreenVCit+α2*Controlsit+μi+υt+ειt

(5)

引入滞后变量ξLn(C/GDP)it-1涵盖了其他可能对碳排放强度产生影响的因素，在很大程度上缓解模型遗漏变量的问题，从而降低计量设定可能存在的设定偏误。另外，考虑到绿色风险投资规模与碳排放强度之间可能存在的内生变量问题，采用两步系统GMM方法(two step sys-GMM)进行估计，将ξLn(C/GDP)it-1及LnGreenVCit视为内生变量，并将这些变量的两阶及更高阶滞后变量作为工具变量。这一回归的结果分别报告在表5的第(3)列。

表5 系统GMM回归结果

但是在有限样本的条件下，两步系统GMM估计仍然有可能造成估计系数向下偏倚的问题。现有研究认为，混合OLS通常会高估被解释变量滞后一阶的回归系数，与之相反，使用固定效应模型回归时则往往会造成被解释变量滞后一阶系数被低估。为此，参考Bond等[28]的检验法则，这一法则提出，如果GMM对被解释变量滞后一阶的估计系数介于固定效应与OLS估计值之间，那么GMM的估计结果就相对较为可靠。为此，表5第(1)列和第(2)列分别提供了带有滞后项的混合OLS 模型估计值和固定效应模型估计值。

从回归结果看，3种方法估计一阶滞后项系数分别为0.799、0.626和0.656，其中GMM估计值大于固定效应估计值而小于混合OLS 估计值，满足Bond等[28]提出的经验法则，可以认为系统GMM方法的估计结果是有效的。此外，Sargan检验和Hansen检验的结果P值分别为0.999和0.696，均明显高于0.1，即工具变量的选择是有效的。同时残差序列相关性检验显示AR(2)的P值大于0.1，表明差分后残差项不存在序列相关性问题。从实证结果看，核心解释变量与被解释变量之间回归系数仍然保持1%水平下显著性，同时系统GMM估计显示回归系数为-0.048 9，二者之间仍然存在显著负相关关系，这表明绿色风险投资规模对碳排放强度的影响在统计上是稳健的。

五、中介效应分析

(一)绿色技术进步的中介效应分析

以上实证结果表明绿色风险投资规模上升降低了碳排放强度。为进一步讨论绿色风险投资对碳排放强度的具体影响机制，本文将绿色专利申请规模和绿色专利申请占比纳入回归，对回归方程(3)和回归方程(4)进行检验，检验结果如表6所示。

表6 绿色专利申请规模及申请占比中介效应回归结果

续表(表6)

在表6的第(1)和第(2)列，首先使用双向固定效应分别对绿色风险投资与绿色专利申请规模、申请占比的关系进行回归。回归结果显示，绿色风险投资规模对绿色专利申请规模和绿色专利申请占比回归系数均在1%水平下显著，且回归系数为正，即绿色风险投资规模的上升促进了绿色专利申请规模和绿色专利申请占比上升，假设2得到验证。

表6的第(3)和第(4)列汇报了使用双向固定效应模型对回归方程(4)的检验结果。从回归结果看，绿色专利申请规模及绿色专利申请占比的回归系数均在1%水平下显著为负，说明绿色专利申请规模及申请占比的上升抑制了碳排放强度。与此同时，在对方程(4)的检验中，核心解释变量绿色风险投资规模的回归系数仍然保持显著为负。综合考虑回归方程(3)和回归方程(4)的检验结果，绿色专利申请规模及绿色专利申请占比均在绿色风险投资与碳排放强度的关系中发挥部分中介效应，假设3得到验证，即绿色风险投资规模上升促进了绿色技术进步，进而实现了碳排放强度下降。

(二)稳健性检验

为证明本文结论的可靠性，同时进一步深入讨论绿色技术进步在绿色风险投资与碳排放强度间的中介作用，将中介变量替换为绿色专利获得规模及绿色专利在全部获得专利中的占比，同时继续使用双向固定效应模型，再次对方程(3)和方程(4)进行检验，回归结果如表7所示。

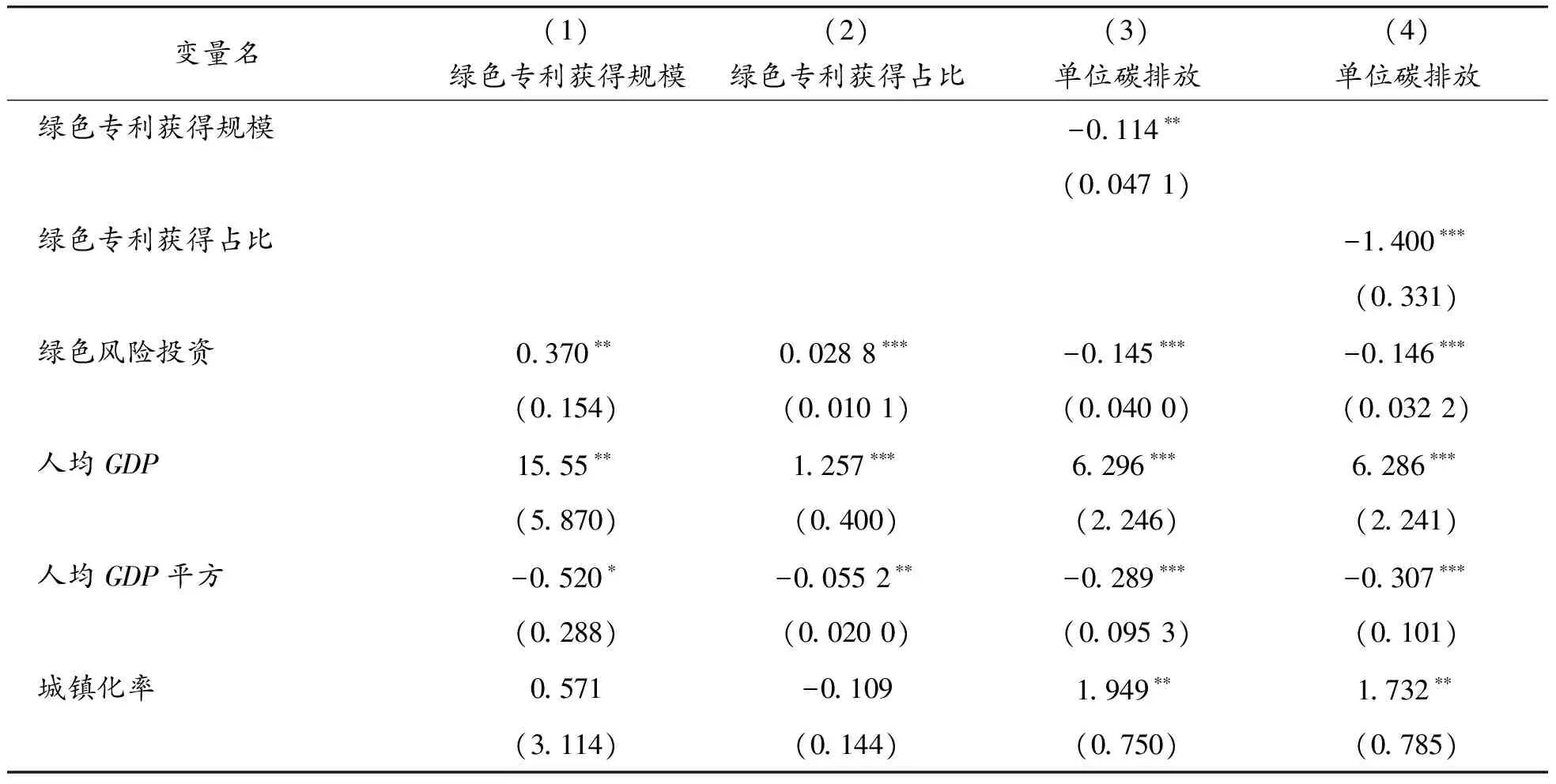
表7 绿色专利获得规模及获得占比中介效应回归结果

续表(表7)

表7的第(1)和第(2)列汇报了绿色风险投资对绿色专利获得规模和获得占比的检验结果。与使用绿色专利申请规模及占比回归得到的结果类似，绿色风险投资对绿色专利获得规模和绿色专利获得占比的回归系数仍为正，且保持一定显著性。同时，将绿色专利获得规模及绿色专利获得占比纳入方程(4)，检验结果汇报在表7第(3)和第(4)列。结果表明绿色专利获得规模及绿色专利获得占比均对碳排放强度存在负向作用，同时绿色风险投资回归系数保持显著为负，即绿色专利获得规模和绿色专利获得占比均在绿色风险投资与碳排放强度的关系中发挥部分中介效应。检验结果表明中介效应回归结果较为可信。

六、结论及政策建议

本文利用2006—2019年28个省(自治区、直辖市)的面板数据，采用双向固定效应模型和中介效应模型，实证研究了绿色风险投资规模变动对碳排放强度的影响。研究结果表明：(1)绿色风险投资规模上升显著抑制了碳排放强度；(2)绿色风险投资上升显著提高了绿色专利申请规模和绿色专利申请占比，即绿色风险投资促进了绿色技术进步；(3)绿色专利申请规模和绿色专利申请占比均在绿色风险投资与碳排放强度的关系中发挥了部分中介效应，绿色风险投资规模上升促进了绿色技术进步，进而实现了碳排放强度下降。

基于以上结论，本文提出如下政策建议：

(1)支持绿色风险投资发展，通过绿色投资促进碳减排。在以政府为主导的绿色金融供给之外，通过发展绿色风险投资，将民间资本汇集于绿色产业中。考虑适当放宽绿色风险投资资金来源，降低绿色风险投资相关税费。同时通过多层次资本市场建设，进一步完善风险投资退出机制，最终实现绿色风险投资与绿色产业发展的良性互动。

(2)加快绿色技术自主创新研发，用创新的方式完成我国经济低碳转型。作为绿色技术创新的供给方，企业部门特别是新兴产业企业部门需要成为政策保护和支持的重点。未来仍需要继续着眼于绿色技术的研发和普及，积极促进产学研相结合，提高企业创新的规模和质量，对企业创新予以鼓励，提高企业部门创新的积极性。

(3)强化绿色金融体系建设与绿色技术创新的协同性。以绿色风险投资发展为抓手，促进绿色金融资源与绿色技术创新相融合。用金融提升创新，以创新实现减碳，完善绿色金融、绿色技术创新和经济低碳化三者之间的协作机制。建议在绿色金融改革创新试验区探索绿色风险投资与绿色技术创新协同推进的新路径，尽快形成可复制、可推广的协同发展经验。