融合粗糙集和RBF神经网络的病毒性肝炎决策分析
2022-05-16吴尚智王旭文
吴尚智,周 运,夏 宁,王旭文,张 帆
(1.西北师范大学计算机科学与工程学院,甘肃兰州 730070;2.广东工商职业技术大学计算机学院,广东肇庆 526020)
病毒性肝炎作为目前流行病学研究的一类易感染疾病,具有极强的传染性,在我国乃至整个世界上都有着很高的关注度[1].人类肝炎病毒有甲型、乙型、丙型、丁型和戊型等之分.肝炎病毒进入人体免疫组织,会导致肝脏组织细胞坏死,轻者会诱发炎症,早期借助药物可以完成治疗,如果患者因不知情而拖沓病情,导致病患加重,会进一步诱发肝纤维化、肝癌等[2].患病程度严重的患者只能通过手术切除病变组织或者更换器官,无疑会加重肝病患者治疗过程中的痛苦,手术前后需要配合高昂的药物治疗,对于医护人员而言,治疗期限的延长无疑加重工作负担.刘红杨等[3]利用差分自回归移动平均与广义回归神经网络组合模型,针对丙型肝炎月发病率完成预测.实验中,将ARIMA模型拟合值作为GRNN模型的输入,实际值作为GRNN模型的输出,对样本进行训练和预测.Lu等[4]先用主成分分析法对光谱数据做特征提取,与循环神经网络相结合,对499名健康人和435名HBV患者进行试验.与此同时,与K近邻算法、支持向量机、随机森林等算法做对比,试验准确率为96.15%,且算法运行稳定.Ebrahimi等[5]利用离散小波变换(DWT)对初始数据集进行多级分解,线性判别分析方法进行数据降维预处理,并提出了利用小波神经网络、不同参数的支持向量机对HCV患者预测,小波神经网络预测准确率为97.14%,支持向量机为98.57%.Wang等[22]提出了基于粗糙集与支持向量机的肝炎诊断方法,知识约简得到的多个属性子集,随后通过组选择算法得到了所需数据集,结果表明RS+SVM组合算法分类准确率为90.7%,与决策树算法、神经网络(NN)做t检验,P值均小于0.05.Polat等[23-24]对病毒性肝炎进行医疗决策,并记录多位学者应用的机器学习算法模型,如LDA、ASR、1-NN、MLP,算法模型就对分类准确率给出对比结果.上述研究表明,针对病毒性肝病识别和分类的研究已有些成果,但是,电子病历在临床记录过程中,研究人员因为跟进不及时、病因特征值缺失等因素,导致数据具有不确定性、强干扰性,这需要确保高维度样本具有很好的医疗决策效果.
文中提出将粗糙集和RBF神经网络结合的方法应用于病毒性肝炎医疗决策分析中,为证明RBF神经网络对属性约简后的病毒性肝炎仍然具有很好的预测效果,文中借助分类准确率和运行时间等评价指标给出了实验结果.
1 理论基础
1.1 粗糙集
粗糙集(Rough set,RS)作为数值分析理论由Pawlak于1982年提出,用于处理模糊和不确定性知识的数学工具[6].
定义1知识与知识库[7]所研究对象组成的非空有限集合构成论域U,对∀X⊆U,称为U中一个概念(包括空集∅),论域中任何概念族通常简称知识.对于一个完整的知识表达系统,即为一个知识库.
粗糙集理论中,将信息表知识表达系统定义为S=U,R,V,f,其中U为论域;R=C∪D为属性集合(C为条件属性集,D为决策属性集为属性值的集合(Vr为属性r的值域);f:U×RV为一个映射函数,通过函数f可以确定U中每一个对象Xt的属性值.
定义2上近似和下近似[7]根据X关于属性集合R的下、上近似值概念,定义
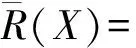

定义3知识的核[8]知识库K(U,R),属性集合R=C∪D,核描述为所有约简的交集,若有一等价关系族P∈R,满足core(R)=∩red(P),则记为等价关系族集P的核.简单来说,核即为等价关系族中所有重要属性的集合.
定义4约简[9]决策表S=(U,C∪D),其中属性C∪D=Φ.令Φ⊂X⊆C,Φ⊂Y⊆D,U/Y≠U/δ={U}(δ是全体划分).若有X0⊆X满足:①SX0(Y)=SX(Y),即决策属性Φ⊂Y⊆D关于条件属性Φ⊂X⊆C的支持子集相等于决策属性Y⊆D关于条件属性X0⊆X的支持子集;②SX(Y)⊃SX(Y),若X′⊂X0⊆X.
按照上述描述,总能找到X的一个极小子集X0,即称X0是X的一个约简.空集∅的约简为∅.
在粗糙集理论中,用上下近似集对不精确范畴近似定义,通过对模糊、不确定知识以集合定义、逼近方式达到知识判断的目的.信息熵是系统不确定信息的量化指标[6].通俗说,熵越大,事件发生概率越低,表明信息所携带的不确定性越大;熵越小,结论与前述相反.
设有随机试验,X1,X2,…,Xn是论域U的一个划分,实验结果中每个Xi有概率pi=P(Xi)出现,简记X=(p1,p2,…,pn).信息源X的信息熵定义为[6]
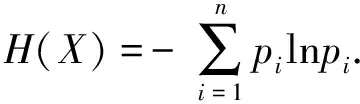
(3)
条件熵:知识Q相对于知识P的条件熵定义为[10]:

1.2 径向基神经网络
径向基(Radial basis function,RBF)神经网络作为现今数据预测应用领域的分类工具,它属于一种3层前向型神经网络:输入层、隐含层、输出层[11],如图1所示:第1层为输入层,文中该层接收多维医疗数据的特征向量,网络结构的输入节点总数即代表着输入数据的维数.在径向基神经网络结构中,输入层与第2层的隐含层间是非线性映射,即M维数据直接非线性映射至第2层.更重要的是,隐含层主要是对神经元传递函数的选择,文中采用表述正态分布的高斯函数,该密度函数定义形式为[12]
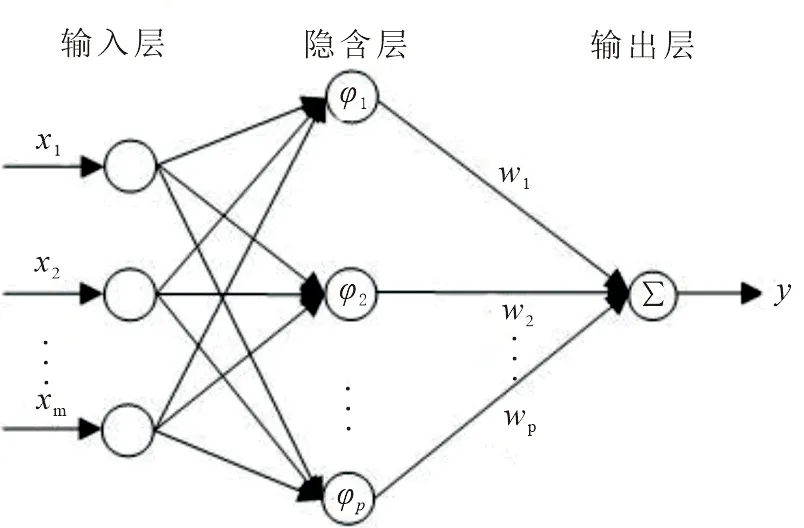
图1 径向基神经网络拓扑
其中,X为网络的输入样本;ci为径向基函数数据中心值;σi为数据宽度.
神经网络结构中最后是输出层,它与第2层通过权值连接,即这两层间采用线性映射的方式建立连接关系.径向基神经网络输出层为隐层节点输出的线性组合[13]:
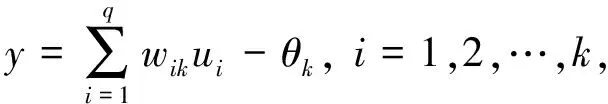
(6)
其中,wik为网络权值;U=(u0,u1,u2,…,uk)T为隐层节点输出;θk为输出层阈值.
2 研究思路和模型设计
2.1 研究思路
为提高病毒性肝炎医疗诊断准确性,文中在缺失数据处理、原始数据集属性约简、预处理后的样本训练等3个方面进行研究.
1)缺失数据处理.为保证病毒性肝炎医疗数据的完整性,进一步提高医疗决策的准确率,文中选用分段线性插值法填充缺失值,线性插值法能够利用两个对象间的线性关系寻找逼近数值,具有简单快捷的优点,避免缺失数据对医疗数据集决策属性分类的影响.
2)原始数据集属性约简.医疗数据往往有着高维属性集合,通过K-Means算法对连续型数值样本离散化处理,提取知识形成决策表;基于条件信息熵的粗糙集特征选择,剔除条件属性中冗余属性,在保证分类能力不变的前提下,使得最小约简集合同原始数据具有相同的决策能力.
3)样本训练.数据预处理后的医疗数据选择径向基神经网络模型训练,最后根据训练结果实现病毒性肝炎医疗决策分析.
2.2 模型设计
首先选取病毒性肝炎医疗数据样本,构建原始决策表,使用分段线性插值方法填充缺失值;其次,设置K-Means方法[14]的迭代求解次数、聚类数目,使用基于距离的聚类分析算法分配对象;然后,用基于条件信息熵的启发式知识约简算法对已经离散化后的决策表属性约简,剔除冗余属性.最后将约简的最小属性集作为RBF神经网络输入层指标,决策属性D作为输出指标,RBF神经网络作为能够拟合任何函数的多层前馈型局部逼近网络,对高维度医疗数据做二分类类别预测.文中提出的粗糙集和RBF神经网络组合模型流程图如图2所示.

图2 RS+RBP神经网络建模流程
2.3 步骤描述
基于条件信息熵的约简算法将条件熵作为启发知识,针对不一致信息决策表,以决策表核为出发点,从非核属性集att中依次挑选剩余属性集合,条件熵较小属性移入核属性集core,并随之将先前挑选出的属性从非核属性集att中剔除.特殊情况下,可能发生多个属性含有相同决策的参考重要度,此时,则选择与约简结果集B组合数最小的属性.若核属性集合存在,属性约简后的结果集条件熵H(D|B)=H(D|C),集合B便存放着试验结果集.
算法时间复杂度主要是通过可辨识矩阵计算决策表核,以及从非核属性集att中依次计算决策属性D相对每个条件属性core∪{Vi}的条件熵.步骤1~5为属性约简描.
步骤1.求解全局条件熵H(D|C),用于终止条件的判断.同时,对离散化后的决策表S,分别设置核属性集core和非核属性集att为空集.
步骤2.计算可辨识矩阵[15],挑选决策属性不等时条件属性组合数目为1的属性作为核.算法开始,令约简结果集B=core.
步骤3.从非核属性集att中挑选每个属性Vi∈att,计算条件熵H(D|B∪{Vi}).
步骤4.寻找出条件熵最小的那个属性(熵越小,表示含有的信息不确定性越小).每挑选出一个核属性Vi,即将该属性从非核属性集att中减去.
步骤5.挑选完整条件属性集合后,记录核属性集合B.终止条件是判断初始条件属性集合的条件熵相等于约简后属性集合的条件熵,若H(D|C)=H(D|B),任务完成,否则转到步骤2.
原始决策表中样本经线性插值填充缺失值、离散化预处理后,再使用基于条件熵的属性约简算法,剔除决策系统中具有不确定、模糊的样本,约简后的样本集合结合泛化性能、容错能力强的RBF网络.文中选取梯度下降法训练前向型径向基神经网络,获得神经网络的3个训练参数最优值.具体算法步骤为6~10.
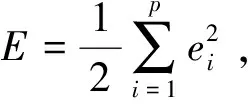

(7)
步骤7.训练以及更新网络中隐含层到输出层节点之间的权值,这一步实际是在求解线性映射函数,从而得到权值系数
其中P为隐含层节点数.
步骤8.训练以及更新网络中隐含层高斯函数的数据中心值
步骤9.训练以及更新网络中隐含层高斯函数的数据宽度
步骤10.径向基神经网络作为一种常用的多层前馈神经网络,每轮训练结束后会得到神经元的误差信号,利用误差反向调整数据中心cj、数据宽度δj以及权值wj,经过多次迭代后,判断总输出误差是否达到预期精度要求.若满足要求,训练所得到的神经网络参数即为最优值.
3 实例数据分析
3.1 数据源及预处理
病毒性肝炎数据集(Hepatitis dataset)来源于UCI数据库.诊断数据给出19个特征指标,构成条件属性C,决策属性D为2分类,No和Yes,该数据集总共155个实例.病毒性肝炎原始数据信息表中的缺失率采用四舍五入方式,精确到小数点数字后两位.由于经典粗糙集只能处理离散型数据,原始信息表中部分指标为No或者Yes(数据表中直接给出简写N和Y)用0,1数值替换,而病毒性肝炎原始数据中同样给出连续型数值特征指标,通过聚类算法完成对象归簇,即离散化方式采用聚类方法.

表1 病毒性肝炎原始数据信息表
病毒性肝炎原始特征信息表对部分条件属性值为No或者Yes的条件属性,通过筛选替换方式可直接完成离散化.年龄取值为7~78,需要进行可视化封装,即重新编码成不同变量,输入第一个分割点位置7,宽度23.667,分成3个区间(图3).

图3 年龄区间分析图
对于处理医疗数据中的缺失值问题,给出5种解决方案:① 简单删除法.对于缺失值太多的实例,为了避免含有太多噪声,直接删除.② 单值插补.即对属性非缺失值求取中位数、均值或者众
数,用于填充缺失值.③ 极大似然估计.在该计算方法中,最常采用的是E-M算法[16].它的使用条件是在数量足够多的大样本中,针对依赖于其它完全变量的随机缺失数据.④ 多重补插法[17].算法基于整个数据集,待插补的特征值具有随机性,缺失数据采用蒙特卡洛方法填充.⑤ 线性插值法[18]. 通过插值函数近似代替原函数,得到待填充数值.
给出多种方案后,考虑到简单删除法和单值插补都会造成原始数据信息浪费,会造成样本信息丢失更多,因此,文中针对条件属性c中的缺失值选用分段线性插值方法填充,插值函数为一次多项式,近似代替原函数[18].与此同时,对其它连续型数值的特征指标,选用基于距离的K-Means聚类算法,设置聚类数为3,迭代次数为100,对距离近的两两对象重新分配,完成类簇.K-Means算法对连续性数值聚类,初始、最终聚类中心变化如表所示.
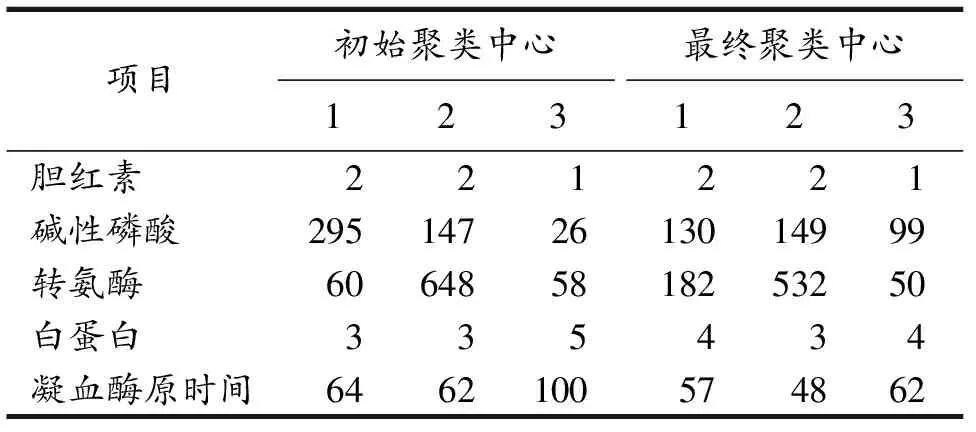
表2 初始、最终聚类中心
3.2 属性约简
通过特征选择剔除条件属性中不必要的特征指标,在保证最小约简集合同原始数据具有相同的决策能力.我们在进行知识约简时,就需要考虑约简集合RED每删掉一个条件属性,是否具有与原集合相同的划分能力,即保证:POSREDmin(D)=POSc(D),这里REDmin为最小属性约简集合,表明最小约简集合在处理完不确定问题时,具有同样的决策能力.对缺失值采用线性插值的方式,K-Means算法对连续性数值聚类,聚类算法设置迭代次数为100,聚类数为3,数据预处理完成后得到离散化后的决策如表3所示.

表3 离散化后的决策表
3.3 实验结果及分析
文中选择的病毒性肝炎医疗数据决策属于2分类问题,通过观察混淆矩阵中4个指标得出初步判断,为了进一步衡量算法模型是否可行,引入准确率acc作为评价指标.表4中,行为真实值,列为预测值.
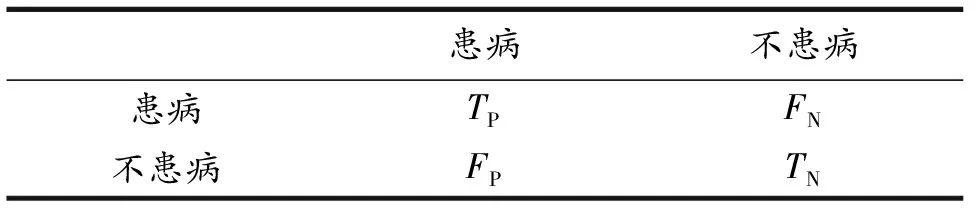
表4 混淆矩阵
对于整个数据模型,使用准确率acc计算模型中判断正确的样本占所有结果值的比重,通过公式可知,分子中的真阳性(TP)和真阴性(TN)比重越大,比例值代表准确率越高[19].
其中,TP为真阳性,即病人正确确诊的个数;TN为真阴性,即健康人诊断无病,被正确地诊断所得的样本个数;FP为假阳性,即健康人被错误地诊断而得样本个数;FN为假阴性,即患者被错误地诊断,所得样本个数.
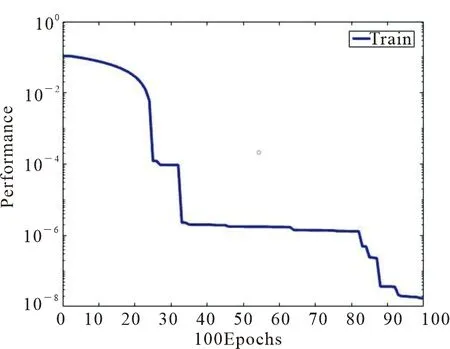
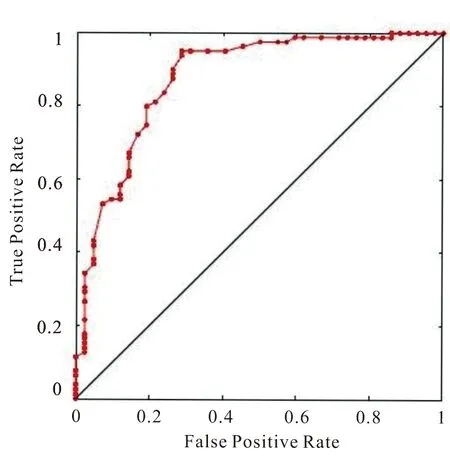
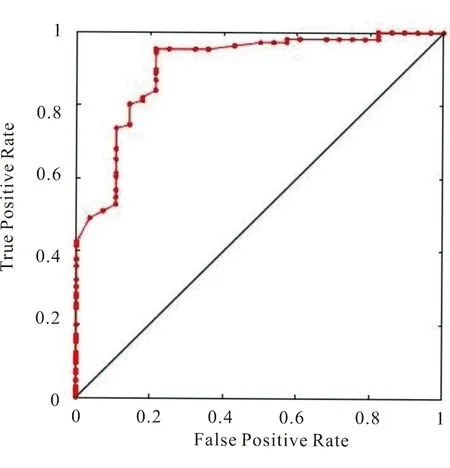
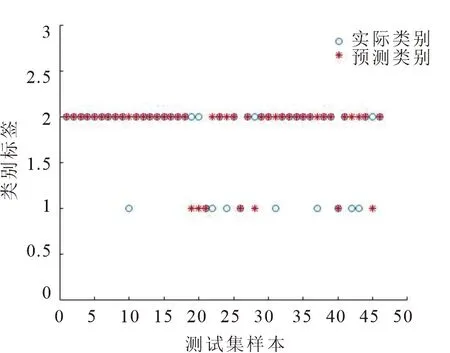
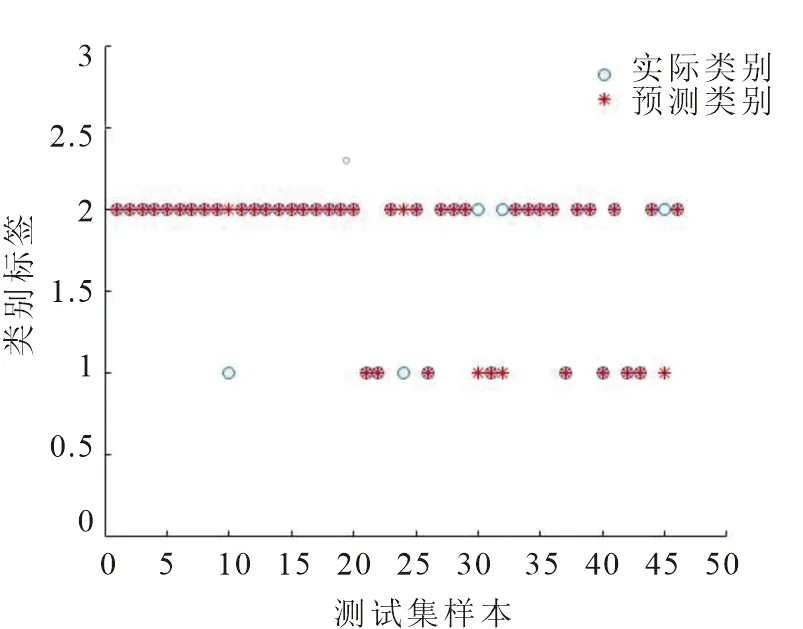
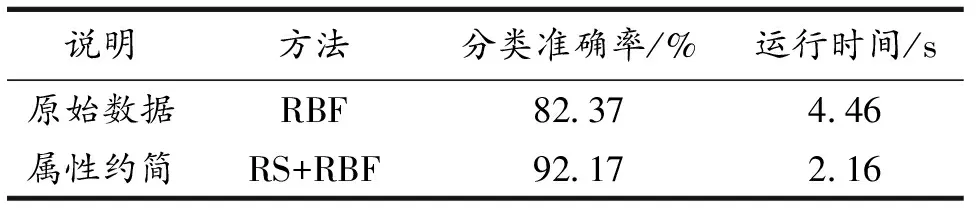
由于广义RBF神经网络要求m 表5 newrb函数参数值试验结果 图4和图5分别给出了病毒性肝炎原始数据和属性约简所得集合分别在同一RBF神经网络模型训练图,纵坐标设置30%比例的测试集合的均方误差值.由图5可知,对原始数据所抽选样本的训练得最佳均方误差值为1.68307×10-8,基于条件信息熵的属性约简算法训练所得均方误差值为3.14357×10-2.而该数值在网络函数性能中的表现反映了在拟合试验中真实值与预测值之间的差异. 图4 原始数据的RBF神经网络训练图 图5 属性约简集合的RBF神经网络训练图 受试者工作特征曲线简称ROC曲线[20].曲线以真阳性率(敏感度TP_rate=TP/(TP+FN))为纵轴,假阳性率(特异性FT_rate=FP/(FP+TN))为横轴,对角线叫做纯机遇线,ROC曲线在对角线上方且距离越远,表明应用该模型效果越好.图6和图7分别表示约简后的样本应用到RS+RBF模型后训练集和测试集的ROC曲线图. 图6 RS+RBF训练集ROC曲线图 图7 RS+RBF测试集ROC曲线图 训练集合中最佳灵敏度和特异性坐标点为(0.19,0.79),AUC值为0.87.测试集合中最佳灵敏度和特异性坐标点为(0.21,0.95),AUC值为0.90,满足0.5<0.90<1条件,证明该组合模型具有预测价值. 选取30%的样本数据对具有相同网络结构的径向基神经网络与组合模型进行测试,对样本分类效果如图8和图9所示.可以明显看出约简后的数据在挑选出最小约简集合后,分类准确率和运行时间评价指标都有很好的优势. 图8 约简前RBF神经网络样本分类效果图 图9 约简后RS+RBF神经网络样本分类效果图 1)分类器对比结果.处理医疗数据并进行医疗决策,由于医疗数据包含缺失值、不确定性、不精确数据.运用基于条件信息熵的属性约简算法,将初始决策表中19个条件属性约简至7个,降低数据集维度,与有着优越的泛化能力,却无法对高维度、冗余数据有效处理的神经网络模型有效结合.RBF神经网络对原始数据训练所得分类准确率为82.37%,运行时间为4.46 s,而使用组合算法所得分类准确率提升至92.17%,运行时间缩减至2.16 s,表6给出约简前后比较结果. 表6 约简样本前后效果对比 2)文中与历史算法对比.通过调查近些年来使用UCI数据库中的病毒性肝病数据集不同算法的应用情况,对算法和分类准确率进行比较,如表7所示. 表7 相同数据集不同算法应用结果对比 粗糙集和径向基神经网络的组合方法应用于病毒性肝炎决策分析,用线性插值法填充数据缺失值,K-Means算法对原始知识决策表中连续性数据完成聚类,离散化处理后的数据进行属性约简,找到最小约简集.由于属性约简的前提是保持拥有与原始知识库相同的分类能力,冗余属性的剔除使得神经网络输入节点减少,简化了神经网络拓扑结构.试验证明,组合模型的应用使得准确率由82.37%提升至92.17%,运行时间由4.46 s缩短至2.16 s,并且训练集、测试集组合模型中AUC值分别为0.87,0.90,可以判断该分类器模型效果较好.该方法可以很好地协助医护人员开展救治工作.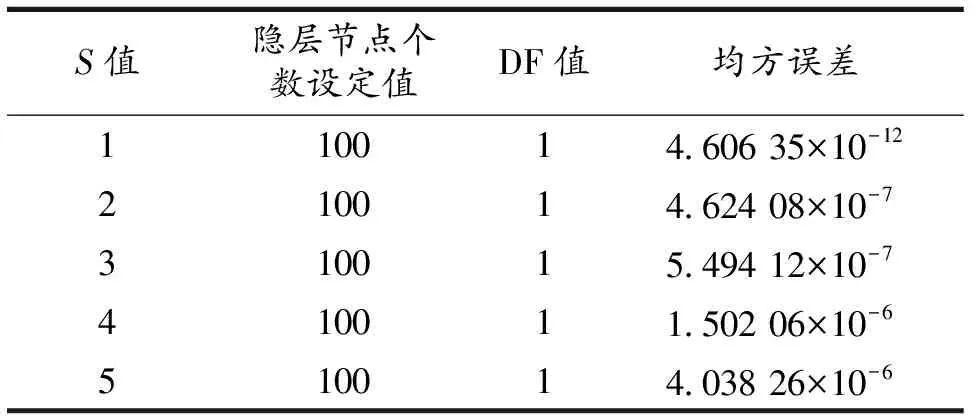


4 结束语
