基于拓扑布置的超高层建筑TTMDI风致振动控制

2022-05-16李春祥曹黎媛

振动与冲击 2022年9期

路畅，李春祥，曹黎媛

(上海大学力学与工程科学学院，上海 200444)

近年来，得益于高强轻质材料的研发与应用，超高层建筑得到繁荣的发展。这些超高层建筑项目不仅给人们的生活带来很大的便利，同时为人口稠密、土地资源有限的特大城市带来发展的新机遇[1]。对于这类细长的超高层结构，柔度大，其固有频率更接近强风的卓越频率，从而发生大幅度的风致振动[2]。特别是，建筑边缘产生的涡旋脱落效应使得超高层结构在横风向产生过度的振动，因此引发的楼层加速度峰值远高于顺风向。为此，抑制超高层建筑在横向风作用下的风致振动并确保横风向水平楼层加速度保持在舒适使用范围内，成为了超高层结构的关键适用性设计要求[3]。

在过去的30年，众多学者们提出了不同的被动控制装置以减小结构的风振响应，其中调谐质量阻尼器(tuned mass damper, TMD)[4-7]由于构造简单且对整体结构影响较小而被广泛地应用于超高层建筑的风致振动控制中。然而，TMD的减振能力在很大程度上取决于惯性质量大小，即惯性质量越大，TMD的控制效果越好且鲁棒性也越强[8]，但对于轻质、细长的超高层建筑，有限的顶层空间限制了大质量块TMD控制装置的应用。为此，Giaralis等[9-11]提出了将调谐质量阻尼惯容器(tuned mass damper-inerter，TMDI)运用到超高层建筑的风致振动控制中。TMDI利用惯容器(Inerter)[12]的质量放大特性，从而在不增加TMD物理质量的情况下实现超高层建筑风致振动控制性能的增强。同时，Cao等[13]将串并联调谐质量阻尼器(tuned tandem mass dampers, TTMD)[14]与惯容器进行集成，提出了一种新型的高性能控制装置：串并联调谐质量阻尼器惯容器(tuned tandem mass dampers-inerters, TTMDI)。通过频域内大量仿真认为：TTMDI系统抑制结构在地面加速度作用下的振动具有较高的有效性和鲁棒性。然而，TTMDI系统控制结构风振反应的性能有待研究。为此，针对易受涡旋脱落影响的细长超高层建筑，本文基于TTMDI控制装置，提出了一种新型的超高层建筑风振控制策略，分别从结构横风向响应分析，以及最优参数设计等方面，对不同拓扑布置策略下的TTMDI超高层建筑风振控制性能逐一展开研究。

1 安装TTMDI超高层建筑的风致动力响应

为了便于更好地说明所提出风振控制策略的基本原理，将超高层建筑简化为一个具有n自由度的线性多自由度(Multiple degrees of freedom, MDOF)系统，如图1所示。

图1 TTMDI-p拓扑下风激超高层建筑集中质量体系模型

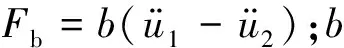
TTMDI装置安装在结构顶层，惯容器控制装置的质量块与结构的第n-p层连接，这样的布置策略称为TTMDI的-p型拓扑。则-p型拓扑下安装TTMDI的MDOF结构的质量、刚度和阻尼矩阵则表示为

(1)

本文仅考虑结构在横风向风荷载作用下的运动方程，则安装TTMDI的MDOF系统运动方程的矩阵表达式为

(2)

式中:x=[x1…xnxt1xt2]T，xi(i=1,2,…,n)为MDOF结构第i层相对地面位移，xt1和xt2分别为TMD1和TMD2质量块相对地面位移；上标“·”为对时间t的一阶导，“¨”为对时间t的二阶导；F=[F1…Fn0 0]T，Fi(i=1,2,…,n)为作用在MDOF结构第i层的横风向风荷载。假设横风向激励是一个平稳随机过程，则根据随机振动频域输入输出关系，安装TTMDI结构的位移和加速度响应功率谱密度可由式(3)计算。

(3)

B(ω)=(K-ω2M+iωC)-1

(4)

于是，安装TTMDI的MDOF结构第k层位移和加速度响应方差为

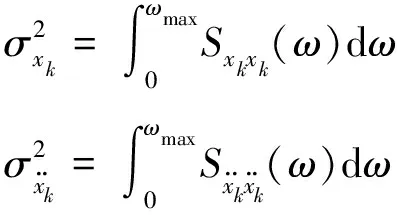
(5)

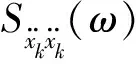
MDOF结构第k层的峰值位移和峰值加速度可由式(6)求得。

(6)

式中,g为峰值系数，可由Davenport提出的经验公式式(7)计算而得。

(7)

式中：ν=2π/ω为有效结构响应频率，Hz，可取为无控结构的一阶固有频率；Twind为假设风作用于结构的持续时间，可取为3 600 s。

2 案例分析

2.1 超高层建筑和风激励模型

本文以某超高层钢结构建筑的风致振动控制作为工程算例，该超高层建筑共74层，层高4 m，总高度296 m，采用(50×50)m2的方形截面。在风荷载作用下，超高层建筑通常建模为多自由度竖直悬臂梁，这一假设在风振响应分析上被广泛采用。工程算例模型如图2所示。其中建筑案例的主要参数如表1所示。

(a)

表1 案例建筑主要参数

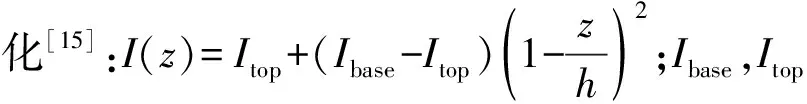
对于提出的矩形截面超高层建筑，高宽比比较大，横风向响应远大于顺风向响应。本文采用Liang等[16]提出的零均值高斯遍历空间相关随机平稳风谱模型来计算结构的横风向风振响应。脉动风荷载功率谱密度矩阵的对角线单元表示为

(8)

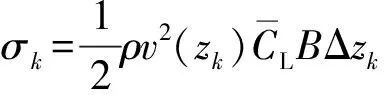
作用在案例结构不同楼层的横风力功率谱密度函数变化曲线，如图3所示。除了第一层和顶层的Δzk为2 m，不同于中间层Δzk为4 m，中间楼层风荷载幅值随着楼层高度的增加而增大，这和平均风速和漩涡脱落频率随楼层高度的变化相同。

图3 作用于案例建筑不同楼层的横风力功率谱密度函数

考虑第k和l层的空间相关性，脉动风荷载功率谱密度矩阵中的非对角线单元表示为

(9)

2.2 控制系统参数优化

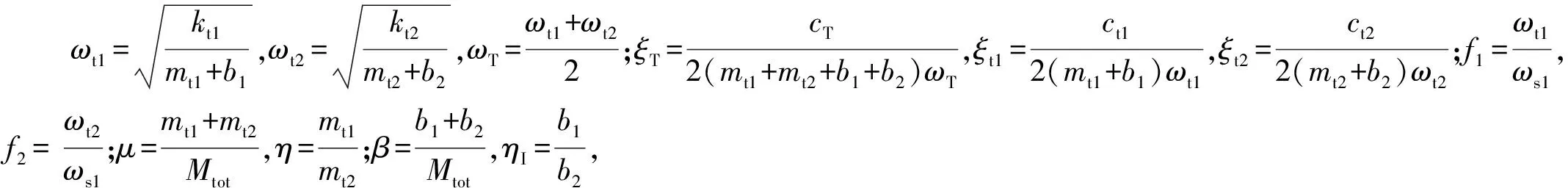
对于超高层建筑，衡量舒适度的风振加速度响应是重要的控制目标。因此，定义TTMDI的优化目标为最小化受控结构顶层横风向峰值加速度(对f1、f2、ξt1、ξt2、ξT和ηI进行优化)，表达如下

(10)

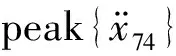
根据惯性力的表达式，惯容器两端加速度差越大，其产生的惯性力就越大，所以考虑TTMDI在多自由结构中的拓扑形式对于超高层建筑风致振动控制是非常重要的因素。为此考虑4种拓扑情况：p=4，p=6，p=8，p=10。为了避免由于两质量块不等造成的非对称性，设定η=1。根据TTMDI最优评价准则，利用模式搜索算法对TTMDI在具有上述频谱特性的风荷载下进行参数优化和数值研究，优化流程如图4所示。并与TMD，TTMD和TMDI进行比较。研究参数和优化参数取值范围如表2所示。值得说明的是：TMD为TMDI在β=0时的特殊情况，TTMD为TTMDI在β=0时的特殊情况。TMD、TTMD和TMDI的目标函数也是最小化结构顶层峰值加速度。

图4 模式搜索法优化流程图

表2 优化参数的取值范围和指定参数值

2.3 减振性能分析

加速度是衡量舒适度的有效指标，为了定量表示安装TTMDI后对结构顶层横风向峰值加速度的控制效果，定义控制有效性Fpa如下

(11)

当质量比μ分别为0.005和0.01时，结构顶层峰值加速度控制有效性Fpa随β-p变化情况,如图5所示。

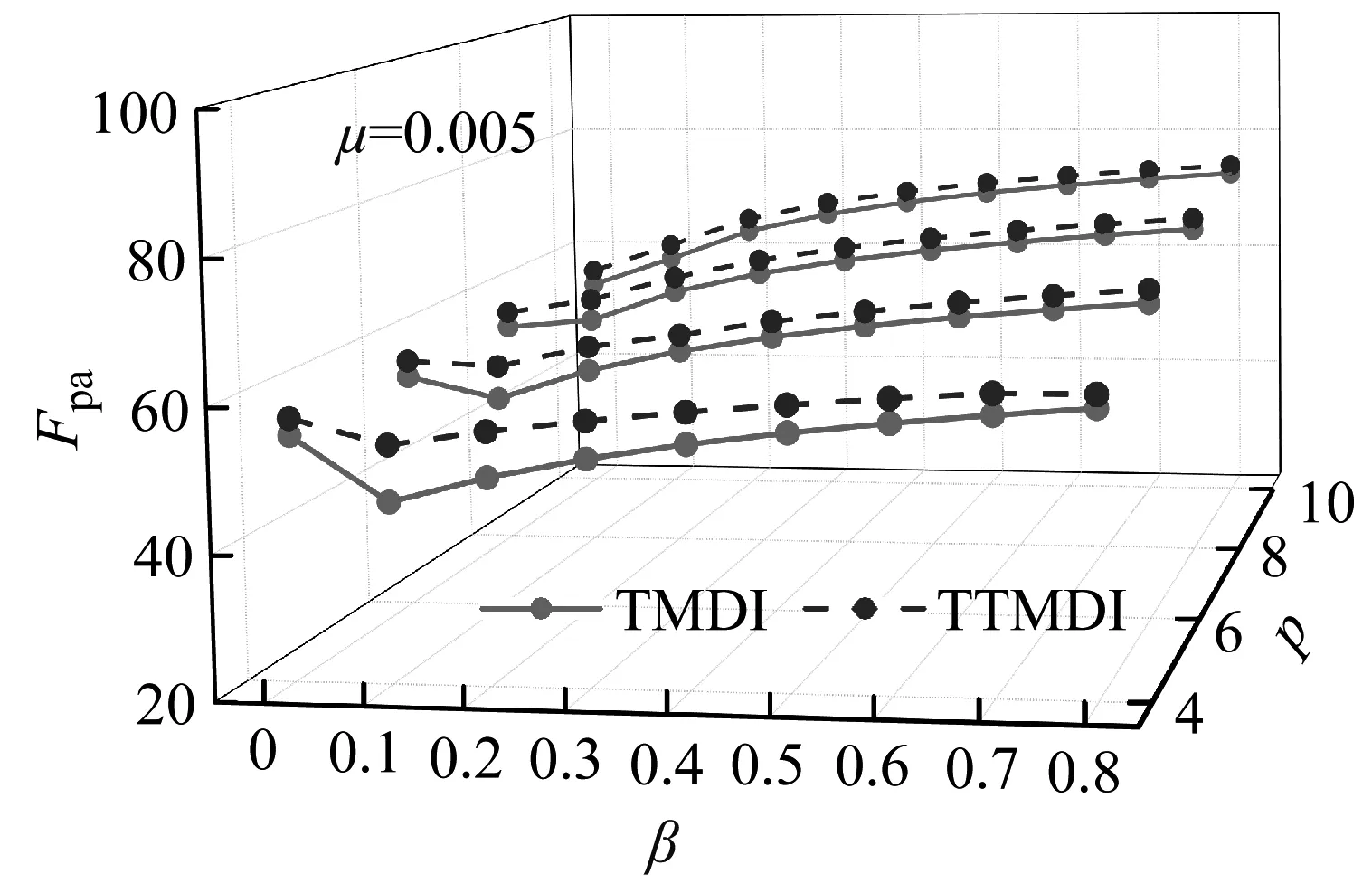
(a)

由图5可知：总体而言，质量块总质量比μ越大，则TTMDI对结构顶层加速度的控制效果越好；当μ值一定时，TTMDI的控制有效性随着总惯容质量比β的增加而增大，其主要原因在于惯容器增加了虚拟质量于控制系统上，极大地提高了其有效惯性质量，从而获得高效的控制效果。从变化趋势可以看出，当μ较小时，TTMDI控制系统可以通过提高β值达到质量块较大时TTMD或TMD的控制效果，所以附加惯容器有利于实现TTMD和TMD装置的轻质化。其次，惯容器连接跨越楼层越多，TTMDI控制有效性越大，原因在于惯容器连接跨越楼层越多，其两端相对加速度差值越大，惯容器对主结构额外施加的惯性力Fb也就越大，从而提高了TTMDI系统的振动抑制能力。此外，在相同的μ和β时，TTMDI系统对结构顶层峰值加速度控制效果要优于TMDI系统，但随着总惯容比β与惯容器连接跨越楼层数的增大，两者的差距随之缩小。

当μ=0.005，μ=0.01时，不同拓扑控制策略下，TTMDI最优刚度随总惯容比β变化趋势,如图6所示。

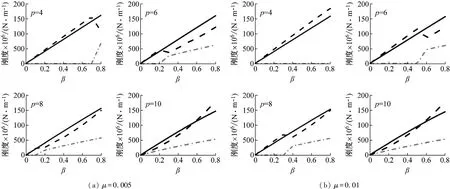
由图6可知：随着β的增加，TTMDI最优刚度变化出现明显的拐点。拐点之前，TMD1所需的kt1趋于0，而TMD2所需kt2与TMDI所需的kt相近。其主要原因是，此时惯容质量比ηI为0，意味着，总的惯容质量集中于与TMD2连接的惯容器上，则TMD2的有效惯性质量要远大于TMD1，TMD2在TTMDI系统中起主要调谐作用，所以TMD2所需刚度要远大于TMD1。拐点之后，由于优化后的ηI为约1.2的值，两个TMD的有效惯性质量没有较大的悬殊，同时起到调谐的作用，所以此时TMD1所需的kt1不为零；而又因为最优调谐频率比f2>f1，所以TMD2所需的kt2仍就大于kt1。另外，从图6可以发现，随着质量块总质量比μ的减小或惯容器连接跨越楼层的增加，拐点出现时所对应的β值越小，甚至消失。其主要原因是，随着μ的减小或惯容器连接跨越楼层的增加，由惯容器所提供的有效惯性质量发挥的作用越大，所以此时存在一个最优的惯容质量分配。整体而言，TTMDI所需总的刚度随着总惯容质量比β的增大而增大，且高于TMDI。

当质量比μ分别为0.005和0.01时，TTMDI和TMDI处于最优状态下所需总阻尼随β-p变化情况，如图7所示。

(a)

TTMDI系统中各最优阻尼系数随β和p的变化趋势,如表3和表4所示。由图和表可知：在前述拐点出现前，最优状态下，TTMDI控制系统中ct2值最大且随着β的增加而迅猛增大，此时相较于ct2，ct1和cT几乎可忽略不计，这也意味着，此时TTMDI系统相当于一个TMDI与一个TMD串并联，其中TMDI发挥着主要的调谐耗能的作用。为此，此时TTMDI系统的总阻尼需求同单个TMDI接近，并随着β的增加而增大。当拐点出现后，最优状态TTMDI系统的耗能机理发生了变化，此时TTMDI的ct1和ct2全为零，cT值较大且随着β的增加而增大，这意味着此时TTMDI系统不同于TMDI，主要通过两质量块之间的连接阻尼耗能；而且相较于TMDI，TTMDI系统对总阻尼的需求不到TMDI系统的一半。这些特性不仅简化了TTMDI系统，而且极大的提高了控制系统的经济性，便利性及可实现性。

表3 μ=0.005时TTMDI最优阻尼系数

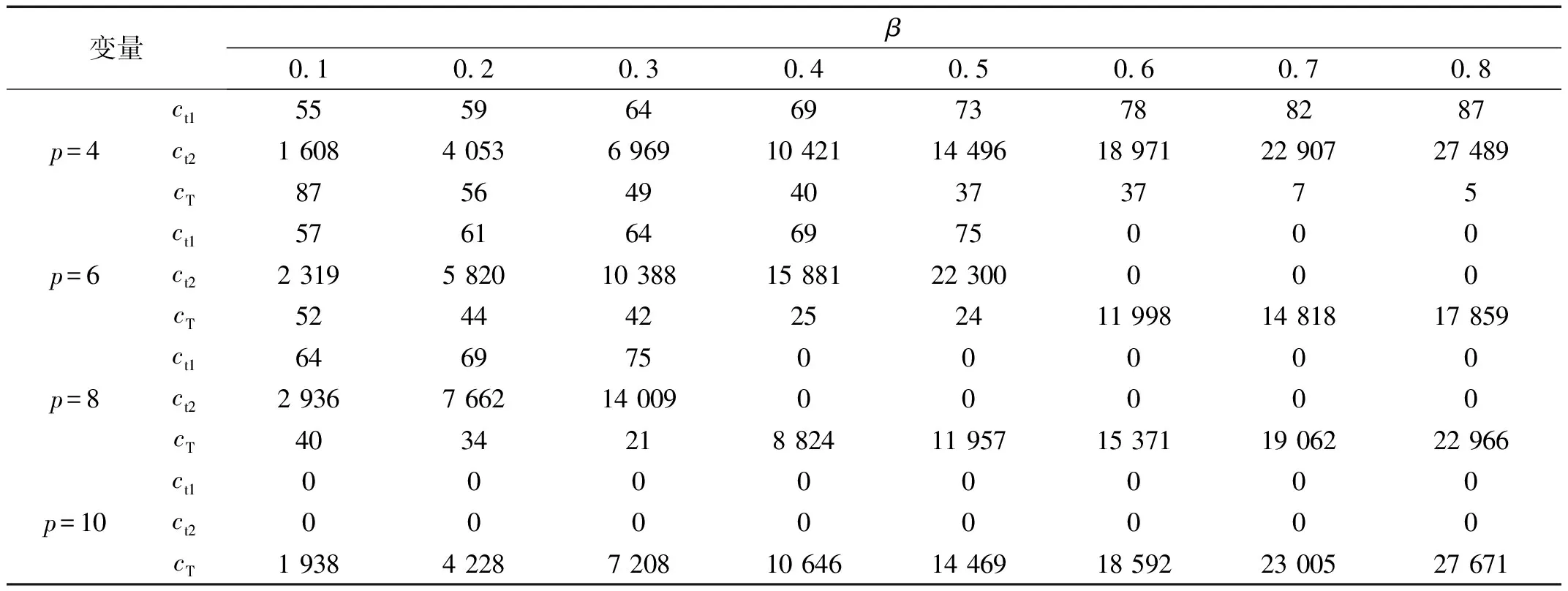
表4 μ=0.01时TTMDI最优阻尼系数

建筑实际设计需要考虑顶部空间的限制，TTMDI质量块的冲程是必须要考虑的。当质量比μ分别为0.005和0.01时，TTMDI处于最优状态下质量块冲程随β-p变化情况，如图8所示。

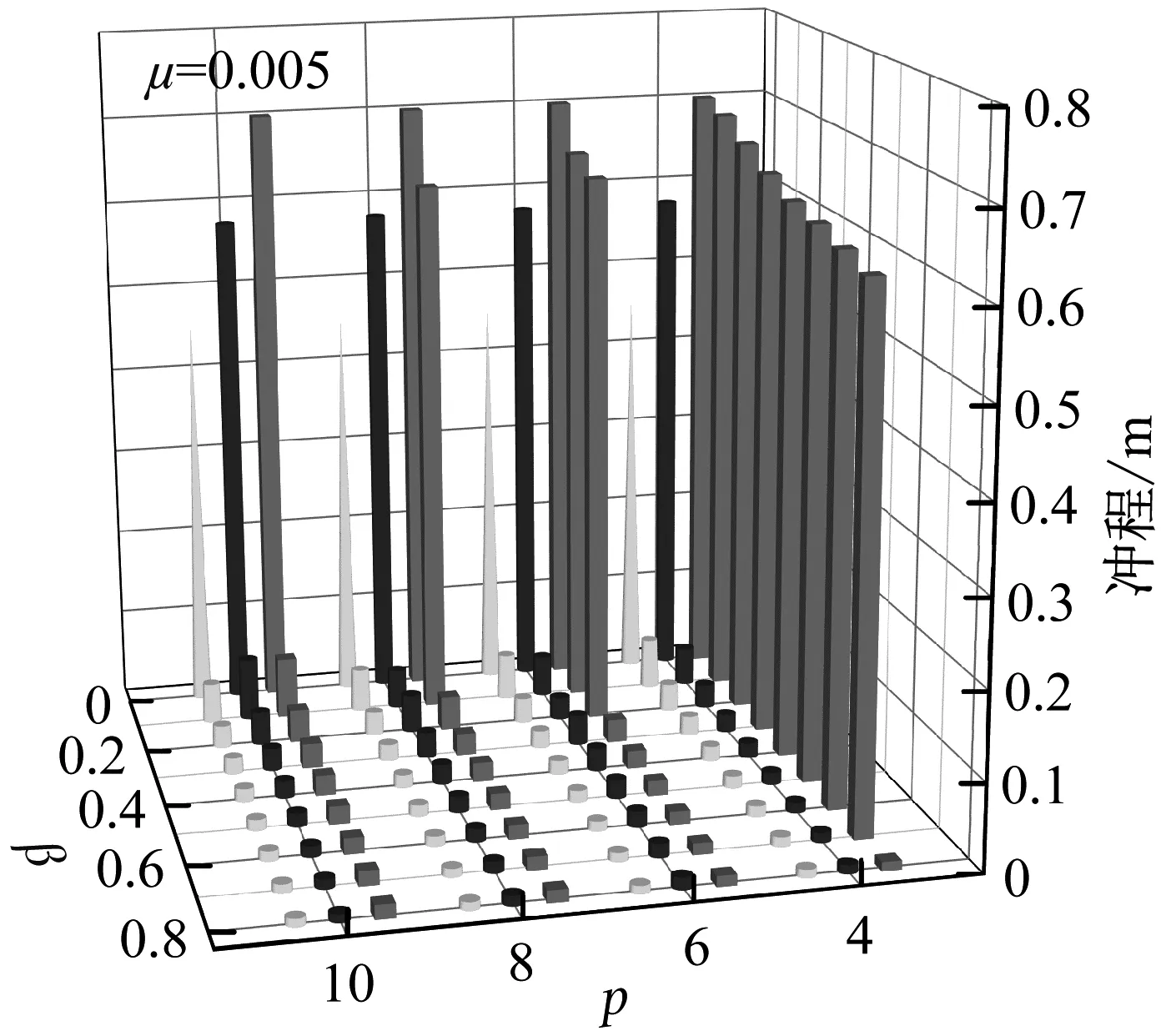
(a)

与图4拐点位置对应，TMD1 冲程骤减处即是拐点位置。由图8可知：在拐点出现前：TTMDI系统中，TMD2则因为连接的刚度和阻尼较大，所以冲程较小；而TMD1由于ct1较小，几乎可视作无阻尼，所以冲程很大。在拐点出现之后，惯容器惯容质量得到重新分配，TMD1和TMD2质量块冲程显著减小，且分布比较均匀，对结构所需空间需求小。总体而言，拐点出现之后，TTMDI的冲程与TMDI的较为接近，都远小于TTMD和TMD的冲程，且随着β和惯容器连接跨越楼层的增加而减小。

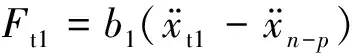
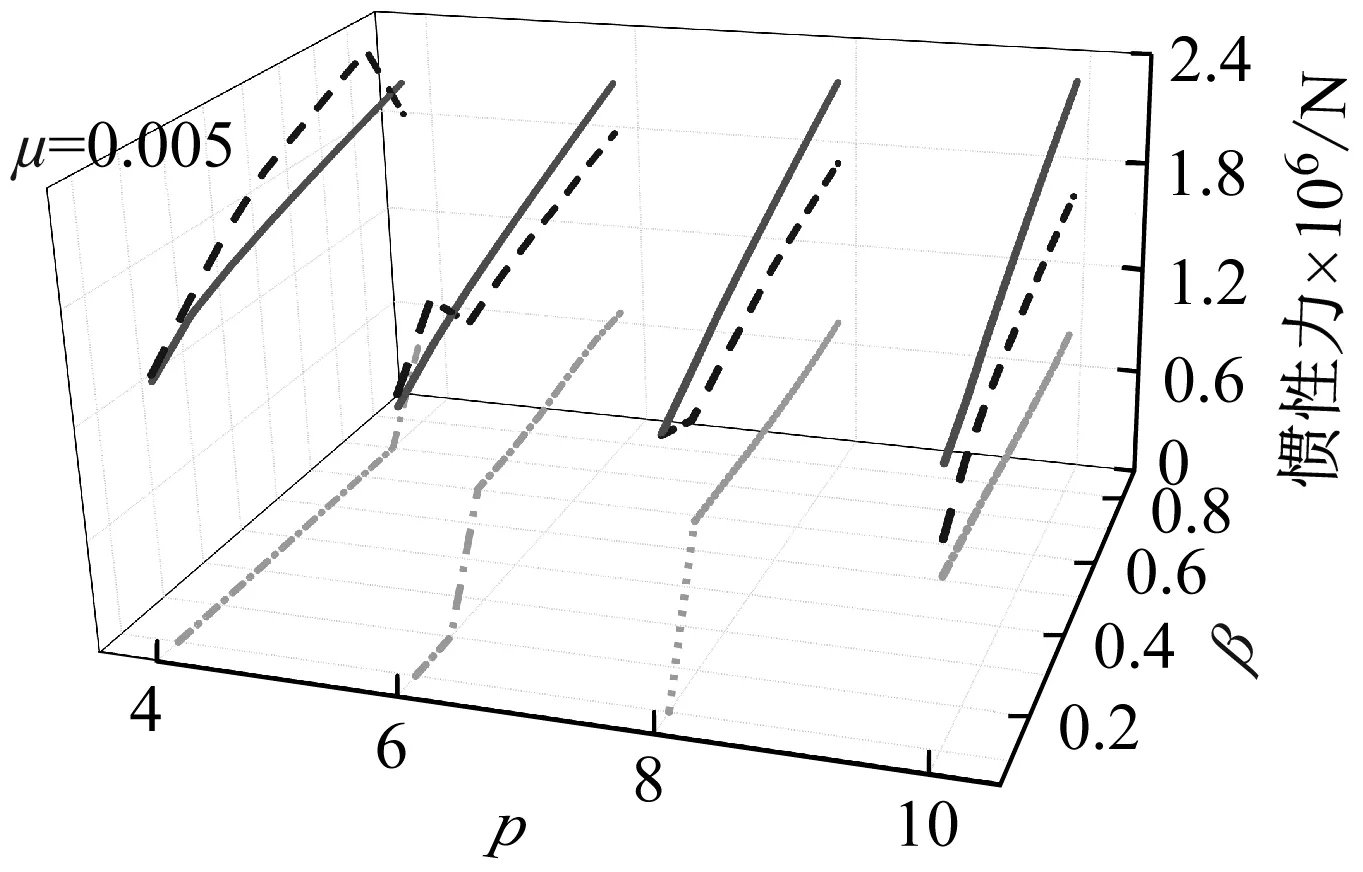
(a)

由图9可知：如前所述，拐点之前由于惯容器的惯容质量集中于与TMD2连接的惯容器上，所以Ft1=0；此时Ft2>Ft，并且随着β增大，差距越发明显。而当拐点之后，惯容器的惯容质量得到重分配，此时与TMD1连接的惯容器开始起作用，所以Ft1突然增大，与此同时Ft2相应减小至低于TMDI的Ft的水平，此时，由图可见TTMDI的各惯容器产生的力都要小于TMDI系统中单个惯容器产生的力。除此以外，μ越小或惯容器连接跨越楼层越多，TTMDI惯容器总的作用在结构上的力就越大，这与TMDI情况相似，不同的是，拐点以后，随着惯容器连接跨越楼层越多，TTMDI的Ft1随之增大而Ft2随之减小，这意味着两惯容器产生的惯性力越发均匀。

μ=0.005,β=0.2,p=8时，在较宽的频率范围内，即无控结构前两阶固有频率范围内，受TMD、TTMD、TMDI、TTMDI控制下结构顶层加速度响应的功率谱密度函数变化曲线,如图10所示。曲线下的面积即为加速度响应方差。

图10表明案例建筑在上述横风向风荷载作用下，结构响应以第一振型为主，高振型对结构总响应的贡献非常小，在风振计算中可以忽略不计；TTMDI控制下功率谱密度函数曲线最低，结构顶层加速度响应最小。

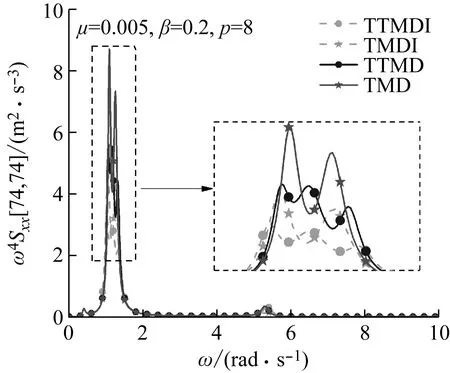
图10 μ=0.005,β=0.2,p=8时，TMD, TTMD, TMDI, 和TTMDI控制下结构顶层加速度功率谱密度函数曲线

为此，图11(a)分别给出了无控和受TMD、TTMD、TMDI、TTMDI控制下结构在第一固有频率附近H(ω)的变化曲线。除了显示给定β=0.5,p=8时不同总质量比μ情况下的结构动力响应外，图11(b)和图11(c)还分别给出受TTMDI控制结构H(ω)随p和β的变化曲线。为了更好的量化频响控制特性，图11(a)局部放大窗口中注释了抑制频带宽[17](suppression bandwidth, SB)：控制系统控制下结构优于无控结构的频率范围。根据这一定义，表5给出了β=0.5,p=8情况下，不同μ时TMD、TTMD、TMDI、TTMDI的抑制带宽，并分别以TMD，TTMD，TMDI为基准，对TTMDI的SB的提高率进行了计算。由图11和表5可以看出：

表5 β=0.5,p=8时不同μ值TMD、TTMD、TMDI和TTMDI抑制频带宽

(a)

(1)对于不同μ值，相较于TMD，TTMD的SB分别增加了34.8%和35.0%；TMDI则分别增加了68.7%和106%；TTMDI则分别增加了103.3%和168.7%。相较于TTMD，TMDI的SB分别增加了25.1%和52.6%；TTMDI则分别增加了50.7%和99.1%。相较于TMDI，TTMDI的SB则分别增加了20.5%和30.4%。显然TTMDI和TMDI控制下结构频率响应曲线明显比TTMD和TMD更低更平坦，其中TTMDI的优势更强一点。说明TTMDI可以在更大的共振频率范围内有效降低结构响应，这表明TTMDI对外部输入激励频率变化具有更好的鲁棒性。

(2)小质量TTMDI(例如μ=0.005)拥有比大质量TMDI(例如μ=0.01)更宽的抑制带宽。

(3)随着p或β的增大，TTMDI的SB增大，加速度传递函数曲线变低且更平缓。

综上所述，考虑到TTMDI控制系统的有效性、冲程和惯性力的大小以及刚度和阻尼参数取值的合理性和经济型，设计参数μ，β及p的建议值,如表6所示。